之前机器学习入门01我们聊了入门第一个学习的KNN算法,而KNN算法是处理分类问题的,那么今天就来解锁新手接触的第一个回归算法——线性回归。
线性回归可以说是机器学习的“基石级算法”,没有复杂的网络结构、没有难理解的激活函数,核心就是“用一条直线(或平面)拟合数据”,学习线性回归算法既能帮我们快速掌握机器学习的核心逻辑(特征、参数、损失、优化),又能直接解决实际中的连续值预测问题(比如房价预测、销量预测)。
1.核心定义:什么是线性回归?
线性回归的本质是用线性关系(直线 / 平面 / 超平面)拟合数据特征与连续预测值之间的关联,通过已知的特征或者标签数据找到这条 “最贴合” 的线性关系,再用它对新特征做连续值预测。
通俗例子:预测房价时,房子「面积」(特征)越大,「房价」(预测值)越高,二者呈现明显的直线趋势。我们用已收集的 “面积 – 房价” 数据找到这条拟合直线,输入新房子的面积,就能通过直线计算出房价预测值,这个过程就是线性回归。
1.1核心线性公式(单特征):
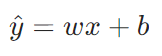
-
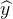 :模型预测值(如预测房价),区别于真实值y
:模型预测值(如预测房价),区别于真实值y -
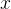 :特征值(如房子面积)
:特征值(如房子面积) -
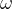 :权重参数(直线的斜率,表征特征对预测值的影响程度)
:权重参数(直线的斜率,表征特征对预测值的影响程度) -
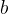 :误差项(指除了线性因素外的随机因素所产生的误差)
:误差项(指除了线性因素外的随机因素所产生的误差)
1.2多特征公式
当预测值受多个特征影响时,公式拓展为多元线性回归:
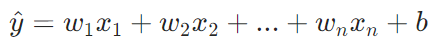
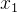 ,
,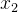 ,…,
,…,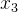 :多个输入特征
:多个输入特征
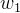 ,
,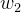 ,…,
,…,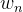 :每个特征对应的权重参数
:每个特征对应的权重参数
2.核心问题:线性回归到底在 “找什么”?
我们都知道线性回归要找一条“最贴合‘’直线,但怎么去找“最贴合”这些数据的直线?
答案很简单:找一组最优的参数,让所有数据到这条直线的“距离差”最小。
而 “最贴合” 的量化标准,是让所有数据的真实值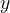 和模型预测值
和模型预测值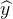 之间的误差(残差)最小—— 这是线性回归的核心目标,所有后续的损失函数、优化算法,都是为了实现这个目标。
之间的误差(残差)最小—— 这是线性回归的核心目标,所有后续的损失函数、优化算法,都是为了实现这个目标。
2.1误差项分析
我们把单个数据的真实值和预测值的差值称为误差项ε(epsilon),核心关系为:
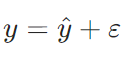
代入公式,可得真实值的完整表达式:
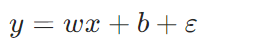
公式的意义:真实值 = 模型线性预测值 + 预测误差,误差项ε表征了模型未拟合到的随机因素
2.2 误差项的核心假设:高斯分布(正态分布)
线性回归能成立,有一个关键前提假设:所有数据的误差项 都服从「均值为 0,方差为
都服从「均值为 0,方差为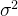 」的高斯分布。
」的高斯分布。
为什么是高斯分布?
因为实际场景中,预测的随机误差是无数个微小独立因素的叠加,根据中心极限定理,这些微小因素的叠加结果必然服从高斯分布。
2.2.1高斯分布的概率密度公式
误差项 ∼N(0,
∼N(0,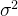 ),其概率密度为:
),其概率密度为:
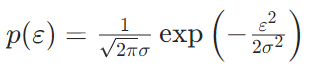
- 误差服从正态分布所以均值为 0:误差的正负波动相互抵消,模型没有系统性偏误(不会一直预测偏高 / 偏低)
- σ:标准差,表征误差的波动大小,σ越小,模型预测越精准
2.3 代入误差:推导真实值的条件概率
们的目标是找到参数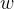 ,
,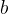 ,让模型拟合的直线能最大概率生成已知的真实数据(这个思想称为最大似然估计),因此需要推导真实值y在特征x和参数
,让模型拟合的直线能最大概率生成已知的真实数据(这个思想称为最大似然估计),因此需要推导真实值y在特征x和参数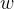 ,
,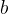 下的条件概率
下的条件概率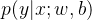 。
。
步骤 1:将误差项 代入高斯分布公式;
代入高斯分布公式;
步骤 2:条件概率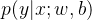 等价于
等价于 (因为x,w,b确定时,
(因为x,w,b确定时, 和
和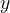 一一对应);
一一对应);
最终推导得到:

这个公式的核心意义:在已知特征x和参数w,b时,模型生成真实值y的概率。我们要找的最优w,b,就是让这个概率对所有数据的乘积最大(最大似然估计)。
3.核心量化:损失函数
通过最大似然估计推导后,会发现让真实值的条件概率乘积最大,等价于让所有数据的 之和最小.
之和最小.
为了标准化这个目标,我们定义线性回归的损失函数(Loss Function)——均方误差(MSE),这是回归问题最常用的损失函数,也是线性回归的标配。
3.1 均方误差(MSE)公式
对于有m个样本的数据集,均方误差损失函数 为:
为:

- 下标
 :第
:第 个样本的真实值
个样本的真实值 、特征
、特征 、预测值
、预测值
 :标准化项,
:标准化项, 是求均值(让损失与样本数无关),
是求均值(让损失与样本数无关), 是为了后续求导时消去平方的系数 2,(简化计算,不影响最优参数的求解)
是为了后续求导时消去平方的系数 2,(简化计算,不影响最优参数的求解)- 核心项
 :平方误差,既保证误差非负,又能放大较大的误差(让模型优先修正预测偏差大的样本)
:平方误差,既保证误差非负,又能放大较大的误差(让模型优先修正预测偏差大的样本)
3.2 损失函数的意义
 是关于参数
是关于参数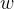 和
和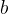 的二次函数,其函数图像是一个凸函数(只有一个最小值点,无局部最优),而线性回归的核心目标,就是找到这个最小值点对应的
的二次函数,其函数图像是一个凸函数(只有一个最小值点,无局部最优),而线性回归的核心目标,就是找到这个最小值点对应的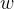 *和
*和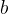 *——最优参数,此时损失函数最小,模型的整体预测误差最小。
*——最优参数,此时损失函数最小,模型的整体预测误差最小。
4.核心求解:找到最优参数
知道了要让损失函数 最小,接下来就是求解最优参数,这里我们使用最小二乘法来计算
最小,接下来就是求解最优参数,这里我们使用最小二乘法来计算
对于线性回归的均方误差损失,存在解析解,可以通过对损失函数求偏导并令偏导为 0,直接解出最优参数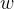 *和
*和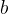 *,这个方法称为最小二乘法。
*,这个方法称为最小二乘法。
对 分别关于
分别关于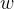 和
和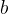 求偏导,令
求偏导,令 、
、 ,解方程组可得:
,解方程组可得:


 :特征x的样本均值,
:特征x的样本均值,
 :真实值y的样本均值,
:真实值y的样本均值,
5.线性回归项目实战
对以上数据建立线性回归模型
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False
data = pd.read_csv("多元线性回归.csv", encoding='gbk', engine='python')
corr = data[["体重", "年龄", "血压收缩"]].corr()
print(corr)
lr_model = LinearRegression()
x = data[['体重', '年龄']]
y = data[['血压收缩']]
lr_model.fit(x, y)
score = lr_model.score(x, y)
print(f"模型R²值:{score:.4f}")
print("单样本预测结果:", lr_model.predict([[80, 60]]))
print("多样本预测结果:", lr_model.predict([[70, 30], [70, 20]]))
a = lr_model.coef_[0]
b = lr_model.intercept_[0]
print(f"线性回归模型为:y = {a[0]:.2f}x1 + {a[1]:.2f}x2 + {b:.2f}")
y_pred = lr_model.predict(x)
plt.figure(figsize=(10, 6))
plt.scatter(y, y_pred, alpha=0.7, color='blue', label='实际值vs预测值')
plt.plot([y.min(), y.max()], [y.min(), y.max()], 'r–', lw=2, label='理想拟合线')
plt.xlabel('血压收缩(实际值)', fontsize=12)
plt.ylabel('血压收缩(预测值)', fontsize=12)
plt.title(f'多元线性回归:实际值 vs 预测值 (R^2 = {score:.4f})', fontsize=14)
plt.legend(fontsize=10)
plt.grid(True, alpha=0.3)
plt.show()


5.1代码详解

先导入相关第三方库,我们的数据集是.csv文件,所以我们使用pandas库,然后是绘图库matplotlib,最后是机器学习必须的sklearn,因为matplotlib不支持中文,所以我们提前设置绘图的字体微软雅黑,然后就导入.csv文件


计算并输出指定变量之间的皮尔逊相关系数矩阵,用于分析变量间的关联性。
体重和血压收缩的相关系数为 0.9064,呈强正相关,说明体重越大,血压收缩值越高,这是最显著的关联。
体重和年龄的相关系数为 -0.7003,呈负相关,说明年龄越大,体重有降低的趋势。
年龄和血压收缩的相关系数为 -0.3828,呈弱负相关,说明年龄对血压收缩的直接影响较小。


创建一个 LinearRegression 类,该模型默认使用最小二乘法来求解回归系数。
“体重” 和 “年龄” 作为模型的x
“血压收缩” 作模型的y
然后调用 fit() 方法,用特征 x 和目标 y 训练模型。模型会通过最小二乘法计算出回归系数和误差项,从而建立从 “体重、年龄” 到 “血压收缩” 的线性关系。
然后输出R²为0.9461


这段代码是用训练好的多元线性回归模型进行预测,并输出结果
当单样本的体重为 80、年龄为 60 时,模型预测的血压收缩值约为 131.97。
当多样本第一个样本:体重 70,年龄 30;第二个样本:体重 70,年龄 20;两个样本对应的预测血压收缩值分别约为 98.60 和 94.60。


这段代码表示提取并输出多元线性回归模型的系数和截距,从而得到完整的线性回归方程


这段代码就是将所有数据和线性回归方程以图表的形式展示。
OK啊,以上就是机器学习线性回归的详细介绍。
日记
2月2日,星期一
吐槽CSDN自带的latex公式编辑器
有到了周一,又是新的一周,又是一句没用的废话,日记就是这么多流水账组成的。
其实今天的博客我写到晚上12点还没有写完,但是现在CSDN有一个活动,每天发一篇博客有流量券,所以我就先把写了一半的提交了,然后再编剧补完,这样也能拿到流量券。
今天敲公式真的是累,我尤其要吐槽一下自带的latex,这个 巨丑,虽然这个公式可以像代码一样输入,但是我输入公式基本都是鼠标点点点,找特殊符号,这里不如AXmath全,而且这个
巨丑,虽然这个公式可以像代码一样输入,但是我输入公式基本都是鼠标点点点,找特殊符号,这里不如AXmath全,而且这个  真的好丑,又不清楚,又小,防止因为我电脑问题,我直接截屏下来吐槽
真的好丑,又不清楚,又小,防止因为我电脑问题,我直接截屏下来吐槽

这个真的丑的要死,我搜狗输入法输出的都比他清楚:ε,你看,latex连狗(搜狗输入法)都不如,真路边一条。
!!!本次对latex公式编辑器的吐槽仅仅是因为我电脑不行,或者我人长得太丑了导致的,与原latex公式编辑器无关!!!(保命声明)
 网硕互联帮助中心
网硕互联帮助中心

![大模型幻觉治理新范式:SCA与[PAUSE]注入技术的深度解析与创新设计-网硕互联帮助中心](https://www.wsisp.com/helps/wp-content/uploads/2026/02/20260202104855-69808117bbda7-220x150.jpg)




评论前必须登录!
注册