从像素到组件：用于视觉表征学习的特征向量掩蔽

文章目录

From Pixels to Components: Eigenvector Masking for Visual Representation Learning
- 预备知识
- 创新点
- 方法实现
- - 步骤 1：数据预处理与 PCA 变换
  - 1.数据输入与标准化
  - 2. 全维度 PCA 变换（无损映射）
  - 步骤 2：基于 “方差占比” 的主成分掩码设计
  - (1) PMAE_ocl（Oracle 最优掩码）
  - (2) PMAE_rd（随机化掩码）
  - 步骤 3：PMAE 模型架构（适配 PC 空间的 ViT encoder-decoder）
  - 1. 编码器（Encoder）：处理“可见成分的像素空间映射”
  - 2. 解码器（Decoder）：重建“掩码主成分”
  - 3. 损失函数：PC 空间的 L2 损失
- 实验

From Pixels to Components: Eigenvector Masking for Visual Representation Learning

论文：https://arxiv.org/abs/2502.06314 会议：https://so.csdn.net/so/search?q=ECCV&spm=1001.2101.3001.7020 年份：2025

预备知识

自监督学习（Self-Supervised Learning, SSL）无需人工标注，通过 “设计辅助任务” 从无标签数据中学习有意义的特征表示，目标是让学习到的表示能迁移到下游任务

主成分分析（PCA）一种线性降维 / 数据变换方法，目标是找到数据中 “方差最大的正交方向（主成分，PC）”，实现数据的低维表示或特征分解

创新点

1.从 “像素局部空间” 转向 “主成分全局空间”，解决语义丢失与冗余问题

传统MIM采用像素块随机掩码（如固定掩码 75% 的 16×16 像素块），存在两大主要问题：

（1）语义完全丢失：小目标（如图像中的小物体、医疗图像中的细胞）可能被掩码块完全覆盖，导致模型无法获取目标语义信息，（如图 1 右侧案例，掩码后图像无任何可识别的物体特征）；在这里插入图片描述图1. 像素空间中的掩码操作。左侧为原始图像，中间为施加随机空间掩码后部分相关信息被移除的图像，右侧为所有语义信息都被移除的图像。后者是一个掩码图像建模（MIM）可能无法学习到有用表征的例子

（2）局部信息冗余：单个像素块常包含背景、纹理等无意义冗余信息，使得 “可见区域 – 掩码区域” 的共享信息与下游任务（如图像分类）所需的高层特征（如物体类别）错位。

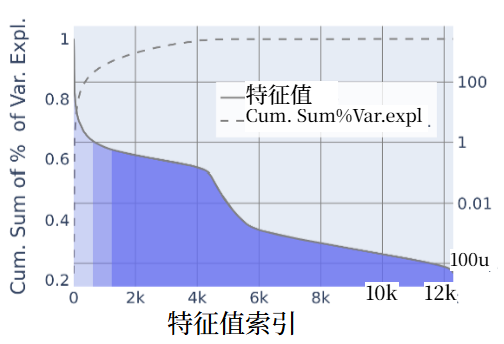
论文中的解决办法首次提出在主成分（PC）空间进行掩码：通过 PCA 将图像从像素空间（局部、冗余）转换为 PC 空间（全局、去冗余），每个主成分对应图像的全局变化模式（如高特征值 PC 捕捉颜色分布、低特征值 PC 捕捉边缘结构，图 2），确保掩码后仍保留目标的部分语义信息，同时避免局部冗余。 vdv 在这里插入图片描述

图2. 从主成分到空间特征。与主成分谱不同区域相关的空间特征概述；图像展示了顶部（浅蓝色）、中部（浅蓝）和底部（深蓝色）主成分所捕捉的特征

利用 PCA 的数学特性实现 “信息的有意义划分”

（1）无相关性与方差可解释性：PCA 生成的主成分彼此不相关，且每个主成分的方差贡献已知（方差占比与特征值成正比），可精准控制掩码的 “信息量”，而非像像素块掩码那样依赖模糊的 “块数量占比”；

（2）全局特征承载：PC 空间的每个维度对应图像的全局特征（如整体亮度、物体轮廓），而非像素块的局部特征（如单个背景区域），使模型在重构掩码成分时必须学习高层全局特征，而非低层次纹理。

2.基于 “方差占比” 的动态掩码，提升超参数鲁棒性与可解释性

传统 MAE 的掩码比例以 “像素块数量” 为基准（如 75% 块掩码），存在两大问题：（1）数据集依赖性强：需针对不同数据集单独调优（如图 3 顶部，75% 掩码在 CIFAR10、TinyImageNet 等数据集上均非最优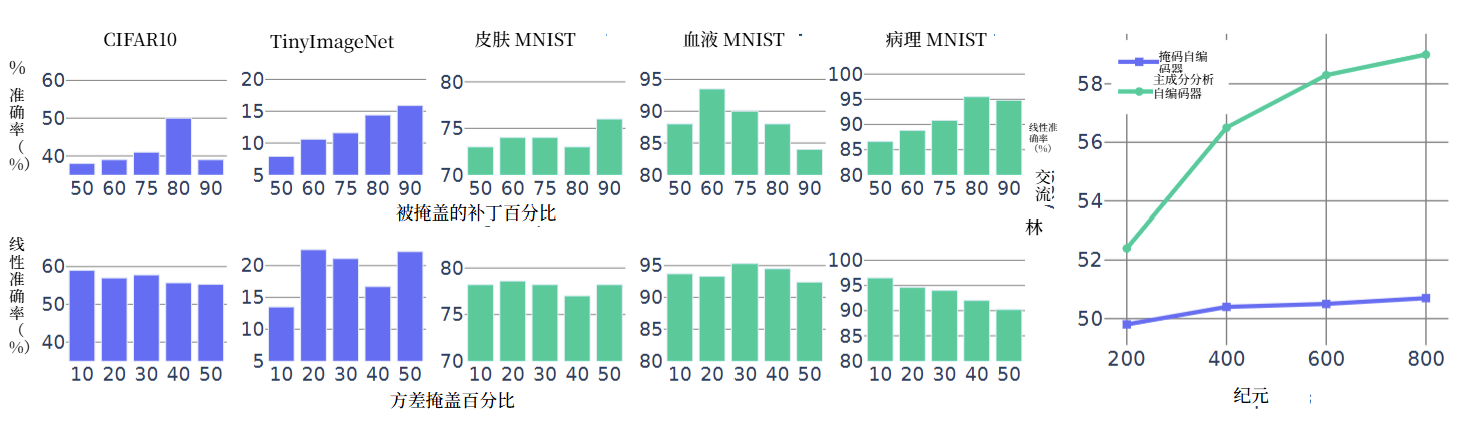）；在这里插入图片描述

图3. 掩码率的影响。不同掩码率下MAE（上）和PMAE（下）的线性探测准确率。掩码率是一个敏感且依赖数据的超参数。虽然很难为MAE提取明确的掩码指导原则，但对于PMAE，我们观察到在20%的数据方差被掩码时，其在各个数据集上的性能接近最优。（右）学习曲线。CIFAR10分类任务在训练轮次中的线性探测准确率。PMAE在200轮后超过了MAE的最终性能

（2）信息量模糊：相同块占比在不同数据集（如简单的 CIFAR10 与复杂的 TinyImageNet）中对应完全不同的信息含量，无法统一解释

论文提出以 “方差占比” 定义掩码比例：随机掩码一组主成分，使其累计贡献数据总方差的固定比例（如 20%），该比例直接对应任务复杂度（方差占比越高，需重构的信息越关键，任务越难）。例如：

（1）在 PMAE_ocl（ oracle 掩码）中，通过验证集线性探测性能确定最优方差掩码比例（多数数据集上 20% 方差掩码接近最优，图 3 底部）；

（2）在 PMAE_rd（随机化掩码）中，每个批次随机采样 10%-90% 的方差掩码比例，无需任何超参数调优。

3.适配 PC 空间的 PMAE 设计，兼容多网络类型

4.目标函数创新：PC 空间损失计算，避免像素空间约束过载

方法实现

步骤 1：数据预处理与 PCA 变换

1.数据输入与标准化

输入图像：均先按数据集训练集的均值和标准差进行标准化，消除像素值量级差异；

数据增强：遵循 MAE 的通用策略，包括 “随机裁剪→双三次插值 resize 回原尺寸→水平翻转”，且训练和评估阶段均保留增强

2. 全维度 PCA 变换（无损映射）

PCA计算：对标准化后的图像数据集，计算其经验协方差矩阵

∑

=

X

⊤

X

\\sum = X^\\top X

$\sum = X^{⊤} X$ （

X

∈

R

N

×

D

X \\in \\mathbb{R}^{N \\times D}

$X \in R^{N \times D}$ ，

N

N

$N$ 为样本数，

D

D

$D$ 为像素维度，如

32

×

32

×

3

=

3072

32 \\times 32 \\times 3 = 3072

$32 \times 32 \times 3 = 3072$ ），通过特征值分解得到：
- 特征向量矩阵 $\\in \\mathbb{R}^{D \\times D} V∈RD×D（列向量为各主成分方向）；$
- 特征值矩阵 $\\Lambda = diag(\\lambda_1, \\dots, \\lambda_D) Λ=diag(λ1,…,λD)（ λ 1 > λ 2 > ⋯ > λ D \\lambda_1 > \\lambda_2 > \\dots > \\lambda_D λ1>λ2>⋯>λD，特征值与主成分的方差贡献成正比）。$
图像到 PC 空间的映射：对单张图像

x

∈

R

D

x \\in \\mathbb{R}^D

$x \in R^{D}$ ，通过

x

P

C

=

x

⋅

V

x_{PC} = x \\cdot V

$x_{PC} = x \cdot V$ 转换为 PC 空间表示（

x

P

C

∈

R

D

x_{PC} \\in \\mathbb{R}^D

$x_{PC} \in R^{D}$ ），该过程为无损变换（保留图像全部信息，区别于 PCA 降维）；
逆变换准备：通过

x

=

x

P

C

⋅

V

⊤

x = x_{PC} \\cdot V^\\top

$x = x_{PC} \cdot V^{⊤}$ 可将 PC 空间表示逆投影回像素空间，为后续编码器输入做准备。

步骤 2：基于 “方差占比” 的主成分掩码设计

传统 MAE 以“像素块数量占比”定义掩码比例（如 75% 块掩码），信息含量模糊且数据集依赖性强；PMAE 则以主成分的累计方差占比定义掩码比例(r)，即：

掩码一组主成分，使其累计贡献数据总方差的(100r%)；
剩余主成分（贡献(100(1 – r)%)方差）作为“可见成分”，用于重建掩码成分。

方差占比直接对应 “信息重要性”，可解释性强（如掩码 20% 方差 = 重建 20% 关键信息），且无需针对不同数据集单独调优。

两种掩码策略：

(1) PMAE_ocl（Oracle 最优掩码）

目标：为特定数据集找到最优方差掩码比例(r_{opt})；
实现：在验证集上通过“线性探测准确率”搜索最优(r)（搜索范围 10%-90%），最终发现多数数据集在(r = 20%)（掩码 20%方差的主成分）时性能接近最优（图 5 底部）；
示例：BloodMNIST 数据集通过 Oracle 搜索，确定(r_{opt} = 15%)，即掩码累计贡献 15%方差的主成分。

(2) PMAE_rd（随机化掩码）

目标：无需超参数调优，验证方法鲁棒性；
实现：每个训练批次独立从区间([0.1, 0.9])（即 10%-90%方差）中均匀采样掩码比例(r)，随机选择对应方差占比的主成分进行掩码；
优势：即使使用子最优(r)，仍能在多数数据集上超越 MAE 的最优调优结果（如表 1，PMAE_rd 在 BloodMNIST 线性探测准确率达 90.0%，高于 MAE_ocl 的 78.6%）。

步骤 3：PMAE 模型架构（适配 PC 空间的 ViT encoder-decoder）

1. 编码器（Encoder）：处理“可见成分的像素空间映射”

输入转换：将“可见主成分

m

⊙

x

P

C

m \\odot x_{PC}

$m ⊙ x_{PC}$ ”通过 PCA 逆变换

t

−

1

(

⋅

)

=

⋅

⋅

V

⊤

t^{-1}(\\cdot) = \\cdot \\cdot V^\\top

$t^{- 1} (\cdot) = \cdot \cdot V^{⊤}$ 投影回像素空间，得到“平滑可见图像”（无传统 MAE 的“黑色块遮挡”，如图 1 底部）；
ViT 编码器结构：采用 ViT-Tiny（ViT-T/8），即：
- 图像分块：将逆投影后的像素图像划分为 8×8 像素的 patches（如 32×32 图像分 4×4=16 个 patch）；
- 嵌入层：每个 patch 通过线性层映射为 192 维嵌入向量（hidden size=192），并添加位置嵌入（捕捉空间位置信息）；
- 编码器层：6 层 Transformer（注意力头数 = 12，中间层维度 = 768），处理嵌入向量后输出全局特征（以 [CLS] token 作为最终表示）。

2. 解码器（Decoder）：重建“掩码主成分”

输入：编码器输出的 [CLS] token 特征 + 掩码成分的位置嵌入（仅需掩码区域的位置信息，降低计算量）；
解码器结构：4 层 Transformer（与编码器参数独立），输出维度与“掩码主成分的维度”一致；
PC 空间投影：将解码器输出通过 PCA 正向变换 $t(\\cdot) = \\cdot \\cdot V t(⋅)=⋅⋅V映射回 PC 空间，得到“预测的掩码主成分”。$

3. 损失函数：PC 空间的 L2 损失

核心原则：仅惩罚“掩码成分”的重建误差，避免可见成分的冗余约束；
损失计算：
L

P

M

A

E

(

x

,

m

;

θ

,

ϕ

)

=

∥

(

1

−

m

)

⊙

[

t

∘

g

θ

∘

f

ϕ

∘

t

−

1

(

m

⊙

t

(

x

)

)

−

t

(

x

)

]

∥

2

2

\\mathcal{L}_{PMAE}(x, m; \\theta, \\phi) = \\left\\| (1 – m) \\odot \\left[ t \\circ g_\\theta \\circ f_\\phi \\circ t^{-1}(m \\odot t(x)) – t(x) \\right] \\right\\|_2^2

$L_{PM A E} (x, m; θ, ϕ) =$

(1−m)⊙[t∘gθ∘fϕ∘t−1(m⊙t(x))−t(x)]

22 其中：

$f_\\phi fϕ为编码器（参数 ϕ \\phi ϕ）， g θ g_\\theta gθ为解码器（参数 θ \\theta θ）；$

$x_{PC} t(x)=xPC（PCA 正向变换）， t − 1 ( ⋅ ) t^{-1}(\\cdot) t−1(⋅)为 PCA 逆变换；$

$m)\\odot \\cdot (1−m)⊙⋅表示仅对掩码区域计算误差，确保模型聚焦于“缺失的关键信息”重建。$

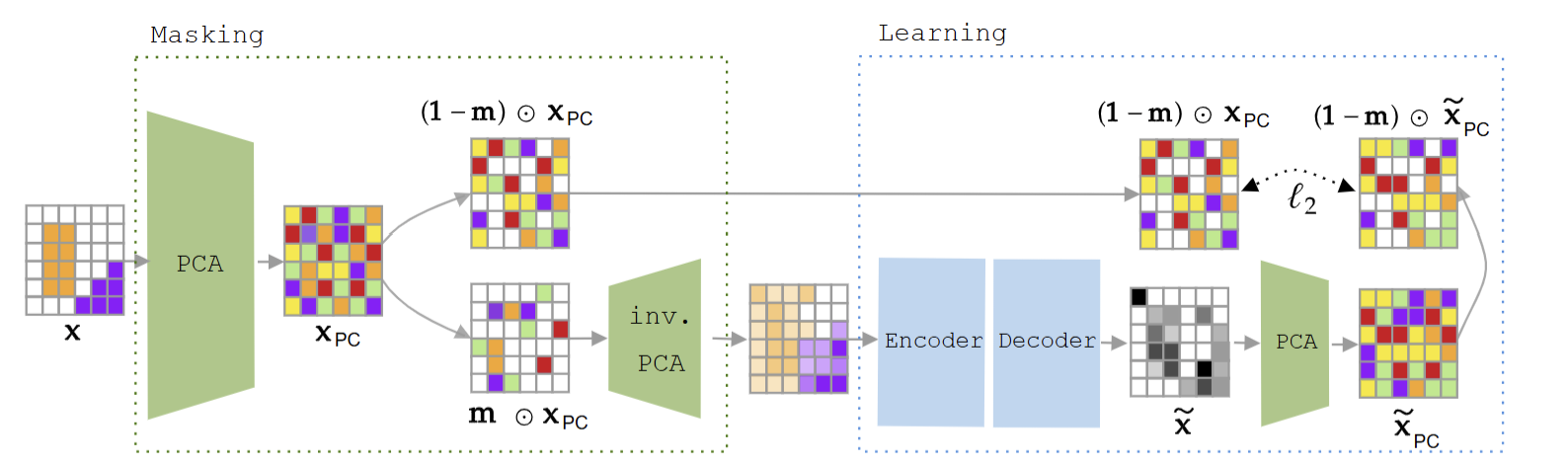
在这里插入图片描述

图4. 主掩码自编码器概述。主掩码自编码器（PMAE）与普通掩码自编码器（MAE）（He等人，2021）的不同之处在于，它在主成分空间而非像素空间中执行掩码操作。可见的主成分随后被投影回观测空间，并作为视觉Transformer（ViT）编码器-解码器架构的输入。被掩码的主成分则作为重构目标

实验

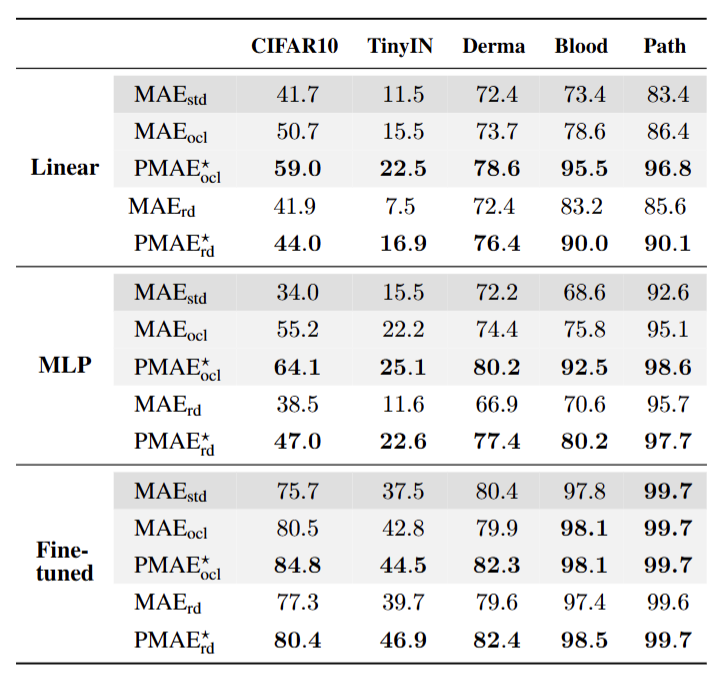核心性能对比：PMAE vs MAE（线性探测）在这里插入图片描述

PMAE全面超越 MAE：平均比 MAE 高 14 个百分点（38% 相对提升），比 MAE ocl高 9.5 个百分点（20.3% 相对提升）；

医疗图像提升最显著，因医疗图像全局特征（如细胞结构、病理纹理）更依赖 PC 空间的全局表示；

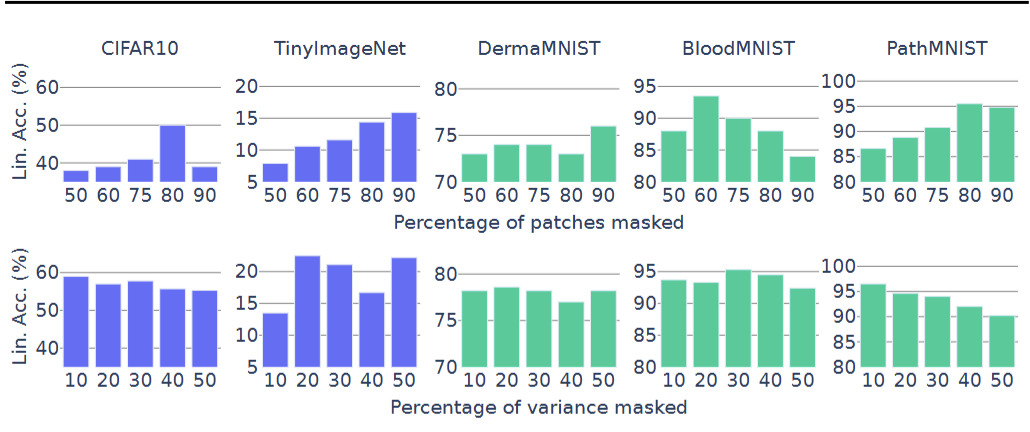
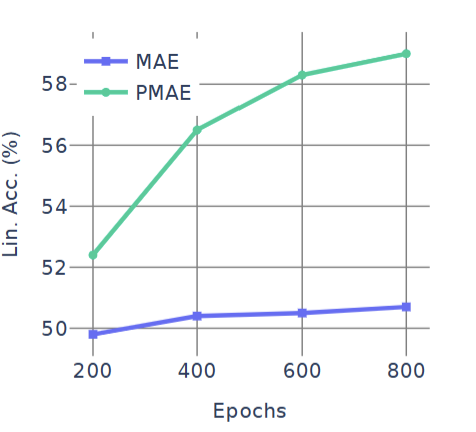
非线性与微调性能验证在这里插入图片描述

图5. 掩码率的影响。不同掩码率下MAE（上）和PMAE（下）的线性探测准确率。掩码率是一个敏感且依赖数据的超参数。虽然很难为MAE提取明确的掩码指导原则，但对于PMAE，我们观察到在20%的数据方差被掩码时，其在各个数据集上的性能接近最优。（右）学习曲线。CIFAR10分类任务在训练轮次中的线性探测准确率。PMAE在200轮后超过了MAE的最终性能

传统 MAE 的 “像素块掩码比例” 是敏感超参，而 PMAE 的 “方差掩码比例” 更鲁棒，结果如图 5 所示：

MAE（图 5 顶部）：最优掩码比例随数据集剧烈波动 ——CIFAR10 最优约 60%，TinyImageNet 约 50%，DermaMNIST 约 40%，无通用规律，需逐数据集调优；
PMAE（图 5 底部）：所有数据集在 “20% 方差掩码” 时接近最优 ——CIFAR10 达 58%，BloodMNIST 达 95%，PathMNIST 达 96%，超参范围 [10%-20%] 内性能稳定，大幅降低应用成本。

PMAE 收敛更快：训练 200 epochs 时，PMAE 的线性探测准确率已超越 MAE 训练 800 epochs 的最终性能（CIFAR10：55% vs 50.7%）；原因：PC 空间掩码聚焦全局高层特征，模型无需学习冗余局部信息，梯度更新更高效。

结论

PC 空间掩码优于像素空间：PMAE 通过 PCA 将图像映射到全局特征空间，避免 MAE “局部冗余”“语义丢失” 的缺陷，使表示更聚焦高层特征（如物体类别、病理结构），在 5 个数据集上均实现性能提升，尤其医疗图像提升显著（平均 + 15 个百分点）。

方差掩码比例更鲁棒、可解释：传统 MAE 的 “像素块比例” 需逐数据集调优，而 PMAE 的 “方差比例” 在 [10%-20%] 内接近最优，且方差占比直接对应 “信息重要性”（如 20% 方差掩码 = 重建 20% 关键信息），解决 MAE 超参敏感的痛点。

PMAE 收敛更快、通用性强：PMAE 训练 200 epochs 即可超越 MAE 800 epochs 的性能，且兼容线性 / 非线性 / 微调多种评估场景；同时，PC 空间的平滑输入适配卷积网络，突破 MAE 仅能使用 ViT 的局限。

从像素到组件：用于视觉表征学习的特征向量掩蔽

文章目录

From Pixels to Components: Eigenvector Masking for Visual Representation Learning

预备知识

创新点