一、概念厘清
| 先验概率 P(ωi) | 无样本观测时,类ωi出现的概率(如 “学校 60% 是男生”) | 贝叶斯公式的初始输入 |
| 后验概率 P(ωi∣x) | 已知样本 x 时,x 来自类ωi的概率 | 决策的直接依据(后验概率最大化) |
| 类概密 p(x∣ωi) | 类ωi条件下,样本 x 的概率密度(连续型) | 描述类内样本分布规律 |
| 似然函数 p(x∣ωi) | 固定 x 时,随ωi变化的函数(与类概密数学形式相同,视角不同) | 似然比决策的核心组件 |
| 证据因子 p(x) | 全概率公式计算的 “样本 x 出现的总概率”,p(x)=∑jP(ωj)p(x∣ωj) | 贝叶斯公式的分母(归一化项) |
| 条件风险 R(αi∣x) | 决策αi(判 x 为ωi)的期望损失,R(αi∣x)=∑jλ(αi,ωj)P(ωj∣x) | 最小风险决策的依据 |
贝叶斯公式:已知先验概率和全概率,求后验概率(用于决策) 全概率公式:当x可能来自多个类时,计算x的总出现概率
二、三大核心决策方法
(一)最小错误率贝叶斯决策:整体平均错误率最小
若
P
(
ω
i
∣
x
)
=
m
a
x
j
P
(
ω
j
∣
x
)
P(ω_i∣x)=max_jP(ω_j∣x)
P(ωi∣x)=maxjP(ωj∣x),则
x
∈
ω
i
x∈ω_i
x∈ωi 等价形式(两分类) ①似然比:
p
(
x
∣
ω
1
)
/
p
(
x
∣
ω
2
)
>
P
(
ω
2
)
/
P
(
ω
1
)
p(x∣ω_1)/p(x∣ω_2)>P(ω_2)/P(ω_1)
p(x∣ω1)/p(x∣ω2)>P(ω2)/P(ω1)(判
ω
1
ω_1
ω1) ②对数似然比:化简计算,避免小数乘法
(二)最小风险贝叶斯决策:考虑损失
引入损失函数
λ
(
α
i
,
ω
j
)
λ(α_i,ω_j)
λ(αi,ωj),条件风险
R
(
α
i
∣
x
)
=
∑
R(α_i∣x)=∑
R(αi∣x)=∑
j
j
j
λ
(
α
i
,
ω
j
)
P
(
ω
j
∣
x
)
λ(α_i,ω_j)P(ω_j∣x)
λ(αi,ωj)P(ωj∣x),x归类于R(αi∣x)最小 与最小错误率的关系:最小错误率是最小风险的特例:当采用 “0-1 损失函数”时等价。
(三)Neyman-Pearson决策:限制关键错误
步骤:
ROC曲线:比较不同分类器性能 横轴:假阳性率 纵轴:真阳性率 关键指标:AUC——ROC曲线下面积 AUC越大,分类器性能越好
三、正态分布的统计决策
1)单变量正态分布
概率密度函数:
p
(
x
)
∼
N
(
μ
,
σ
2
)
p(x)∼N(μ,σ^2)
p(x)∼N(μ,σ2),p(x)=
1
2
π
σ
e
x
p
[
−
1
2
(
x
−
μ
σ
)
2
]
\\frac{1}{\\sqrt{2\\pi}σ}exp[−\\frac{1}{2}(\\frac{x-\\mu}{\\sigma})^2]
2π
σ1exp[−21(σx−μ)2]
2)多元正态分布
概率密度函数:
p
(
x
)
∼
N
(
μ
,
Σ
)
p(x)∼N(μ,Σ)
p(x)∼N(μ,Σ) p(x)=
1
(
2
π
)
d
/
2
∣
Σ
∣
1
/
2
e
x
p
[
−
1
2
(
x
−
μ
)
T
Σ
−
1
(
x
−
μ
)
]
\\frac{1}{(2π)^{d/2}|Σ|^{1/2}}exp[−\\frac{1}{2}(x-\\mu)^T\\Sigma^{-1}(x-\\mu)]
(2π)d/2∣Σ∣1/21exp[−21(x−μ)TΣ−1(x−μ)] 其中,μ:d 维均值向量;Σ:d×d 协方差矩阵(对称正定)
性质:
(
x
−
μ
)
T
Σ
−
1
(
x
−
μ
)
(x-\\mu)^T\\Sigma^{-1}(x-\\mu)
(x−μ)TΣ−1(x−μ)=常数,对应超椭球面(中心为μ,形状由Σ决定)。
x
i
x_i
xi,
x
j
x_j
xj不相关(协方差
σ
i
j
σ_{ij}
σij=0),则它们独立(仅正态分布满足)。
3)正态分布下的决策面分布
| 1.
Σ 1 Σ_1 Σ1= Σ 2 Σ_2 Σ2= σ 2 σ^2 σ2I(对角阵,方差相同) |
线性超平面 | 欧氏距离:
∥ x − μ i ∥ 2 ∥x−μ_i∥^2 ∥x−μi∥2 |
样本各特征独立,分散程度相同 |
| 2.
Σ 1 = Σ 2 = Σ Σ_1=Σ_2=Σ Σ1=Σ2=Σ(非对角阵,协方差相同) |
线性超平面 | 马氏距离平方:
( x − μ i ) T Σ − 1 ( x − μ i ) (x−μ_i)^TΣ^{−1}(x−μ_i) (x−μi)TΣ−1(x−μi) |
样本特征相关,分散形状 / 大小相同 |
| 3.
Σ 1 ≠ Σ 2 Σ_1≠Σ_2 Σ1=Σ2(协方差不同) |
二次超曲面(超椭圆、双曲线等) | 二次判别函数:含
x T W x x^TWx xTWx项 |
样本分散形状 / 大小不同 |
分类器的错误率
仅当类概密为正态分布且协方差矩阵相等时,可通过马氏距离计算错误率: 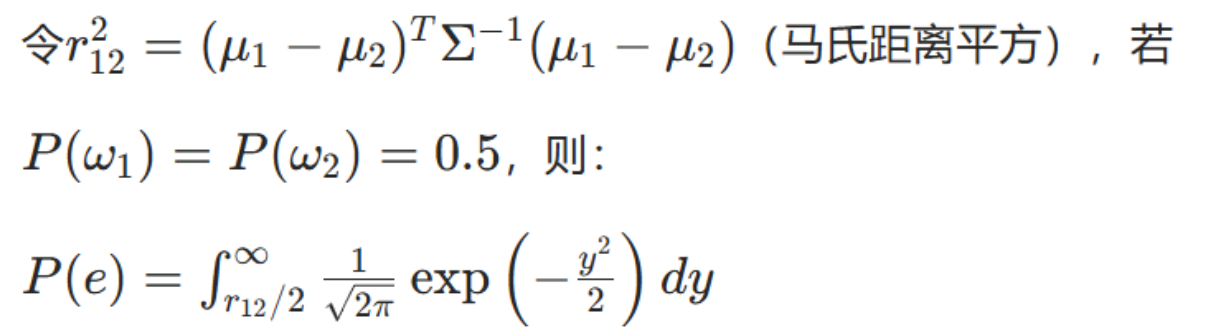
(通过标准正态分布函数Φ查表或近似计算)
写在结尾:最后公式懒得打就放图了哈哈哈 另外,这个专栏马上就到尾声了,大家后面想看什么内容?欢迎留言~
 网硕互联帮助中心
网硕互联帮助中心


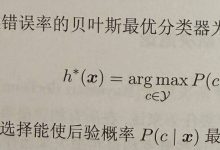


评论前必须登录!
注册