推荐直接网站在线阅读:https://aicoting.cn
在机器学习中,评估指标用于量化模型在不同任务上的性能,是模型选择与调优的重要依据。不同类型的任务对应不同的指标:分类任务常用准确率、精确率、召回率、F1 值以及 ROC-AUC 等,用于衡量模型对不同类别的识别能力;回归任务常用均方误差(MSE)、平均绝对误差(MAE)和决定系数(R²)来评价预测值与真实值的偏差;聚类任务则可采用轮廓系数、归一化互信息(NMI)和调整兰德指数(ARI)来衡量聚类结果的紧密性和一致性。通过合理选择和综合使用这些评估指标,可以全面反映模型性能,指导模型优化和应用。
分类
在分类任务中,模型的目标是将样本正确地划分到预定义类别。为了全面评估模型性能,研究者通常使用一系列分类评估指标。不同指标关注的方面不同,合理选择指标可以帮助发现模型的优势与不足,并指导模型调优。
混淆矩阵(Confusion Matrix)
混淆矩阵是分类模型评估的基础工具,它以表格形式展示模型预测结果与真实标签的对应关系。对于二分类问题,矩阵通常包含四个元素:
- TP(True Positive):真实为正例,预测为正例的样本数。
- TN(True Negative):真实为负例,预测为负例的样本数。
- FP(False Positive):真实为负例,预测为正例的样本数。
- FN(False Negative):真实为正例,预测为负例的样本数。
混淆矩阵不仅能够直观展示分类错误类型,还为后续指标计算提供基础。
准确率(Accuracy)
准确率是模型正确预测样本的比例。
Accuracy
=
T
P
+
T
N
T
P
+
T
N
+
F
P
+
F
N
\\text{Accuracy} = \\frac{TP + TN}{TP + TN + FP + FN}
Accuracy=TP+TN+FP+FNTP+TN
这个很直观,就是别管我预测负样本对了,还是预测正样本对了,都算进来,算的就是预测对的样本占总样本的比例,但是对于类别不平衡的数据,准确率可能具有误导性。例如在正负样本比例严重不平衡时,模型即使总是预测多数类也能获得高准确率。
精确率(Precision)
精确率的定义是在所有被模型预测为正例的样本中,实际为正例的比例。
Precision
=
T
P
T
P
+
F
P
\\text{Precision} = \\frac{TP}{TP + FP}
Precision=TP+FPTP
精确率关注模型预测为正类的样本中,实际为正类的比例,是对模型“猜对”正类的能力的衡量。
召回率(Recall)或敏感度(Sensitivity)
召回率是在所有真实正例中,被模型正确预测为正例的比例。
Recall
=
T
P
T
P
+
F
N
\\text{Recall} = \\frac{TP}{TP + FN}
Recall=TP+FNTP
召回率用于衡量模型对正类样本的覆盖能力,高召回率意味着漏报少,比如疾病筛查中,尽量保证病人被正确识别,即使可能出现少量误报。
F1 值(F1 Score)
F1 值是精确率和召回率的调和平均数,用于综合衡量模型在精确性和召回性上的表现。
F1
=
2
⋅
Precision
⋅
Recall
Precision
+
Recall
\\text{F1} = 2 \\cdot \\frac{\\text{Precision} \\cdot \\text{Recall}}{\\text{Precision} + \\text{Recall}}
F1=2⋅Precision+RecallPrecision⋅Recall
当精确率和召回率不均衡时,F1 值提供了一个综合指标,更适合类别不平衡问题。
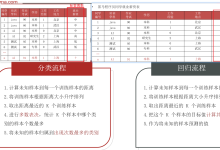
劈里啪啦说了一大堆,是不是不太好理解,现在我们还是用鸢尾花分类举一个例子: 我们假设做一个二分类任务:将 Iris-versicolor 视为正类(1),其它两类视为负类(0)。
| 1 | 1 | 1 |
| 2 | 1 | 1 |
| 3 | 1 | 0 |
| 4 | 0 | 0 |
| 5 | 0 | 1 |
| 6 | 0 | 0 |
根据上表,计算 TP、TN、FP、FN:
- TP(True Positive) = 2 (预测为 1,真实为 1)
- TN(True Negative) = 2 (预测为 0,真实为 0)
- FP(False Positive) = 1 (预测为 1,真实为 0)
- FN(False Negative) = 1 (预测为 0,真实为 1)
说人话,也就是:
- TP:模型成功抓到正类,比如正确识别出一朵 Iris-versicolor。
- FP:模型“误抓”,把其他种类误认为 Iris-versicolor。
- FN:模型“漏抓”,把正类当成了负类。
- TN:模型正确拒绝,负类预测为负类。
混淆矩阵如下:
| 真实 0 | TN = 2 | FP = 1 |
| 真实 1 | FN = 1 | TP = 2 |
准确率
Accuracy
=
T
P
+
T
N
T
P
+
T
N
+
F
P
+
F
N
=
2
+
2
2
+
2
+
1
+
1
=
0.6667
\\text{Accuracy} = \\frac{TP + TN}{TP + TN + FP + FN} = \\frac{2+2}{2+2+1+1} = 0.6667
Accuracy=TP+TN+FP+FNTP+TN=2+2+1+12+2=0.6667
模型总体正确率约 66.7%。
精确率
Precision
=
T
P
T
P
+
F
P
=
2
2
+
1
=
0.6667
\\text{Precision} = \\frac{TP}{TP + FP} = \\frac{2}{2+1} = 0.6667
Precision=TP+FPTP=2+12=0.6667
也就是在模型预测为 Iris-versicolor 的样本中,有 2⁄3 是正确的。
召回率
Recall
=
T
P
T
P
+
F
N
=
2
2
+
1
=
0.6667
\\text{Recall} = \\frac{TP}{TP + FN} = \\frac{2}{2+1} = 0.6667
Recall=TP+FNTP=2+12=0.6667
模型找出了 2⁄3 的真实 Iris-versicolor 样本,还有 1 个漏掉。
F1 值
F1
=
2
⋅
Precision
⋅
Recall
Precision
+
Recall
=
0.6667
\\text{F1} = 2 \\cdot \\frac{\\text{Precision} \\cdot \\text{Recall}}{\\text{Precision} + \\text{Recall}} = 0.6667
F1=2⋅Precision+RecallPrecision⋅Recall=0.6667
F1 值综合考虑了精确率和召回率,用一个数衡量模型整体性能。
通过混淆矩阵和这些指标,你可以直观地看到模型在哪些样本上表现好,哪些样本容易出错,从而决定是否需要调参或改进特征。
ROC 曲线与 AUC
- ROC 曲线(Receiver Operating Characteristic):横轴为假阳性率(FPR),纵轴为真正率(TPR),展示分类器在不同阈值下的性能。
FPR
=
F
P
F
P
+
T
N
,
TPR
=
T
P
T
P
+
F
N
\\text{FPR} = \\frac{FP}{FP + TN}, \\quad \\text{TPR} = \\frac{TP}{TP + FN}
FPR=FP+TNFP,TPR=TP+FNTP
- AUC(Area Under Curve):ROC 曲线下的面积,范围在 0.5(随机猜测)到 1(完美分类)之间。
AUC 可以衡量分类器对正负样本的区分能力,不依赖特定阈值,适合模型比较。
下面我们使用 scikit-learn 绘制 ROC 曲线并计算 AUC,我们以 Iris 数据集的二分类任务 为例,将 Iris-versicolor 作为正类。
# 导入必要库
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import roc_curve, roc_auc_score
# 1. 加载数据
iris = load_iris()
X = iris.data
y = (iris.target == 1).astype(int) # 将 Iris-versicolor 作为正类
# 2. 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# 3. 训练逻辑回归模型
model = LogisticRegression(solver='liblinear')
model.fit(X_train, y_train)
# 4. 获取预测概率(正类概率)
y_prob = model.predict_proba(X_test)[:, 1]
# 5. 计算 ROC 曲线
fpr, tpr, thresholds = roc_curve(y_test, y_prob)
# 6. 计算 AUC
auc_score = roc_auc_score(y_test, y_prob)
print(f"AUC = {auc_score:.4f}")
# 7. 可视化 ROC 曲线
plt.figure(figsize=(6,6))
plt.plot(fpr, tpr, color='blue', lw=2, label=f'ROC curve (AUC = {auc_score:.4f})')
plt.plot([0,1], [0,1], color='gray', linestyle='–', label='Random Guess')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve')
plt.legend(loc='lower right')
plt.grid(True)
plt.show()
结果如下图,ROC 曲线展示模型在不同阈值下的分类能力。曲线越靠近左上角,说明模型越好。AUC=0.81 表示模型区分正负类的能力较强。 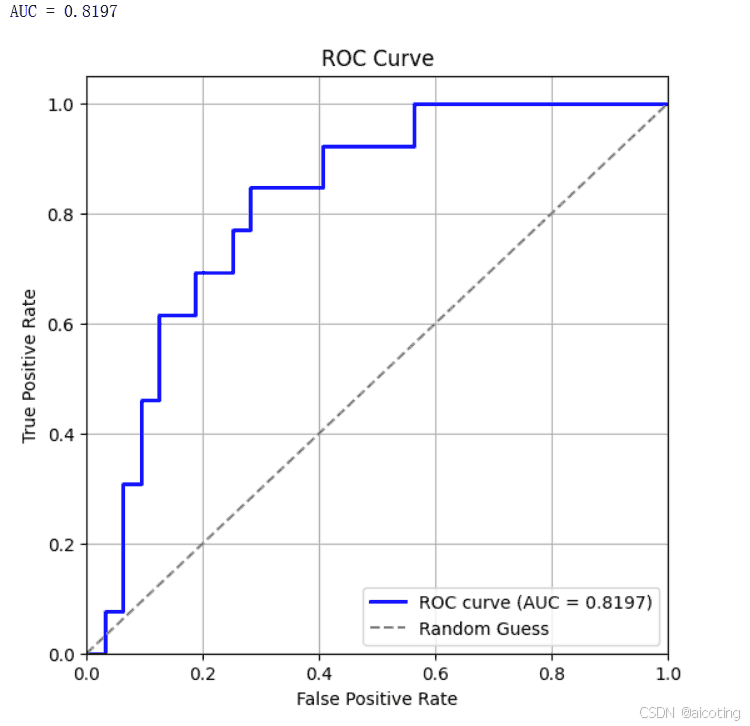
多分类指标
对于多分类任务,常用方法有:
- 宏平均(Macro Average):对每个类别计算指标,再取平均,关注每个类别的重要性相同。
- 微平均(Micro Average):对所有样本统计总的 TP、FP、FN,再计算指标,适合类别样本不均衡时使用。
对于类别均衡的数据,准确率可以作为主要指标。对于类别不平衡的数据,应关注 精确率、召回率、F1 值,必要时使用 ROC-AUC。
分类评估指标提供了从不同角度衡量模型性能的工具。从混淆矩阵到精确率、召回率、F1 值,再到 ROC-AUC,多维度评估可以帮助研究者理解模型优势与不足,为模型优化、调参和选择提供依据。合理的指标选择能够确保模型在实际应用中既准确又可靠。
回归
在回归任务中,模型的目标是预测连续数值。为了衡量回归模型的性能,通常采用一系列量化指标,这些指标可以反映预测值与真实值之间的差异和模型的拟合能力。合理选择和理解回归评估指标,有助于优化模型和提升预测精度。
均方误差(Mean Squared Error, MSE)
MSE 是预测值与真实值误差平方的平均值,计算公式为
MSE
=
1
n
∑
i
=
1
n
(
y
i
−
y
^
i
)
2
\\text{MSE} = \\frac{1}{n} \\sum_{i=1}^{n} (y_i – \\hat{y}_i)^2
MSE=n1∑i=1n(yi−y^i)2
其中为真实值,为预测值,为样本数。
非常好理解,MSE就是计算真实值与预测值之间的差异大小,越大肯定预测的越不准,MSE对较大误差更敏感,适合对异常值敏感的场景,比如线性回归、神经网络的损失函数。
均方根误差(Root Mean Squared Error, RMSE)
RMSE 是 MSE 的平方根,使指标与原始数据单位一致,更易解释。
RMSE
=
MSE
\\text{RMSE} = \\sqrt{\\text{MSE}}
RMSE=MSE
RMSE保留了 MSE 对大误差敏感的特性,同时量纲与原数据一致,直观反映预测误差大小。
平均绝对误差(Mean Absolute Error, MAE)
MAE 是预测值与真实值误差绝对值的平均值。
MAE
=
1
n
∑
i
=
1
n
∣
y
i
−
y
^
i
∣
\\text{MAE} = \\frac{1}{n} \\sum_{i=1}^{n} |y_i – \\hat{y}_i|
MAE=n1∑i=1n∣yi−y^i∣
它对异常值不如 MSE 敏感,更稳健,适用于异常值较多或希望均衡衡量误差的场景。
决定系数(R² Score, Coefficient of Determination)
R
2
R^2
R2衡量模型对数据方差的解释能力,取值范围通常在 0 到 1 之间,越接近 1 表示模型拟合越好。
R
2
=
1
−
∑
i
=
1
n
(
y
i
−
y
^
i
)
2
∑
i
=
1
n
(
y
i
−
y
ˉ
)
2
R^2 = 1 – \\frac{\\sum_{i=1}^{n}(y_i – \\hat{y}_i)^2}{\\sum_{i=1}^{n}(y_i – \\bar{y})^2}
R2=1−∑i=1n(yi−yˉ)2∑i=1n(yi−y^i)2
其中为真实值平均数。
R
2
=
0
R^2 = 0
R2=0表示模型仅预测均值,
R
2
=
1
R^2 = 1
R2=1表示预测完全正确。
注意,
R
2
R^2
R2对异常值敏感,负值可能出现,表示模型表现比均值预测还差。
平均绝对百分比误差(Mean Absolute Percentage Error, MAPE)
MAPE 衡量预测误差占真实值的百分比,适合对相对误差关注的场景。
MAPE可以直观显示预测偏离真实值的比例,但是当真实值接近 0 时,MAPE 会非常大甚至无法计算。
光说不练瞎把式,下面我们使用 波士顿房价数据集 算一下上面的常用回归评估指标。
# 导入必要库
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_boston # 新版本可用 fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
# 1. 加载数据
try:
boston = load_boston()
X, y = boston.data, boston.target
except:
from sklearn.datasets import fetch_california_housing
cali = fetch_california_housing()
X, y = cali.data, cali.target
# 2. 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# 3. 训练线性回归模型
model = LinearRegression()
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
# 4. 计算回归评估指标
mse = mean_squared_error(y_test, y_pred)
rmse = np.sqrt(mse)
mae = mean_absolute_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
mape = np.mean(np.abs((y_test – y_pred) / y_test)) * 100
print(f"MSE: {mse:.4f}")
print(f"RMSE: {rmse:.4f}")
print(f"MAE: {mae:.4f}")
print(f"R²: {r2:.4f}")
print(f"MAPE: {mape:.2f}%")
# 5. 可视化预测误差
plt.figure(figsize=(8,6))
plt.scatter(y_test, y_pred, color='skyblue', edgecolor='k')
plt.plot([min(y_test), max(y_test)], [min(y_test), max(y_test)], color='red', lw=2, linestyle='–')
plt.xlabel("True Values")
plt.ylabel("Predicted Values")
plt.title("True vs Predicted Values")
plt.grid(True)
plt.show()
# 6. 可视化误差分布
errors = y_test – y_pred
plt.figure(figsize=(8,6))
plt.hist(errors, bins=20, color='lightcoral', edgecolor='k')
plt.xlabel("Prediction Error")
plt.ylabel("Frequency")
plt.title("Distribution of Prediction Errors")
plt.grid(True)
plt.show()
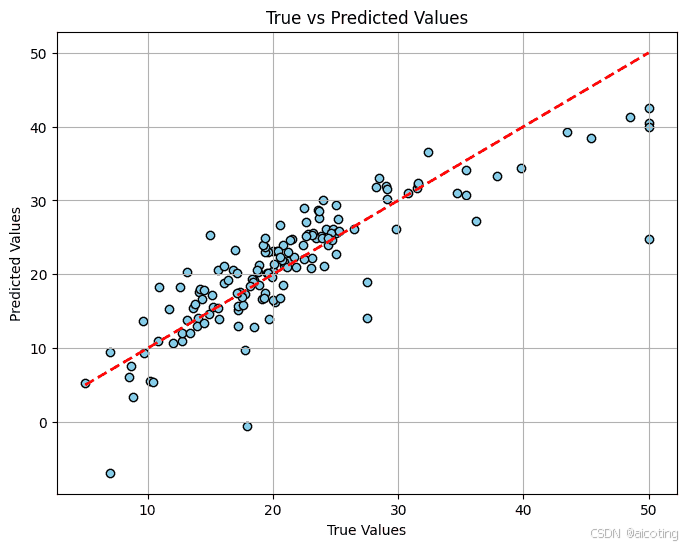
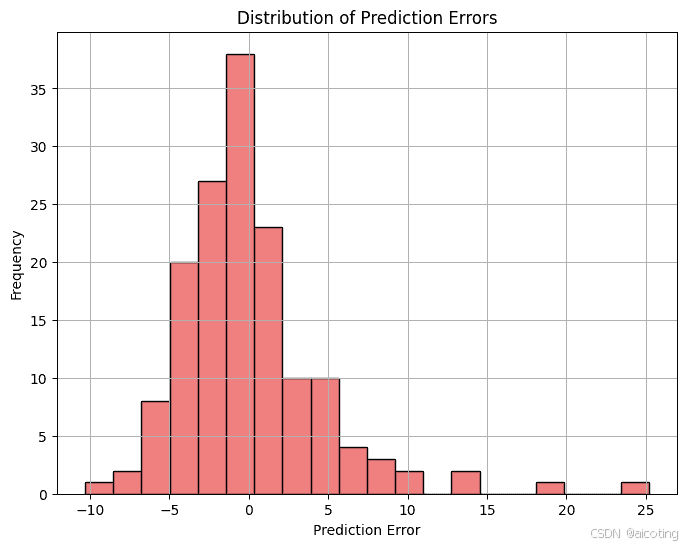
结果如下,第一个图中预测点落在红色虚线
附近表示预测的准确,偏离线越远表示误差越大,第二个误差分布直方图展示预测误差的分布,中心集中表示模型预测稳定,偏离大表示存在异常预测。

总结一下,回归评估指标提供了从不同角度衡量模型预测效果的工具。从绝对误差(MAE)、平方误差(MSE、RMSE)到解释方差的
R
2
R^2
R2 ,再到相对误差 MAPE,每种指标都有其特点和适用场景。
聚类
聚类是一种无监督学习方法,其目标是将数据样本划分为若干组,使得同一组内部的样本相似度尽可能高,而不同组之间的样本差异尽可能大。由于聚类通常没有真实标签,评估聚类质量需要使用专门的指标。根据是否依赖真实标签,聚类评估指标可以分为 外部指标 和 内部指标。
内部指标(Internal Metrics)
内部指标只使用数据本身和聚类结果进行评估,不依赖真实标签,主要关注簇内紧密度和簇间分离度。
轮廓系数(Silhouette Coefficient)
定义:衡量每个样本与自身簇内其他样本的相似度,与其与最近簇样本的相似度差异。
s
(
i
)
=
b
(
i
)
−
a
(
i
)
max
{
a
(
i
)
,
b
(
i
)
}
s(i) = \\frac{b(i) – a(i)}{\\max\\{a(i), b(i)\\}}
s(i)=max{a(i),b(i)}b(i)−a(i)
-
a
(
i
)
a(i)
a(i) :样本i
i
i 到同簇内其他样本的平均距离。 -
b
(
i
)
b(i)
b(i) :样本i
i
i 到最近簇的平均距离。 -
s
(
i
)
s(i)
s(i) 范围:[-1, 1],越接近 1 表示聚类效果越好。 高轮廓系数表示簇内样本紧密且簇间分离明显,负值表示样本可能被错误分配。
Calinski-Harabasz 指数(CH Index)
CH
=
Tr
(
B
k
)
/
(
k
−
1
)
Tr
(
W
k
)
/
(
n
−
k
)
\\text{CH} = \\frac{\\text{Tr}(B_k) / (k-1)}{\\text{Tr}(W_k) / (n-k)}
CH=Tr(Wk)/(n−k)Tr(Bk)/(k−1)
定义:衡量簇间离散度与簇内紧密度之比。
-
B
k
B_k
Bk :簇间散布矩阵 -
W
k
W_k
Wk :簇内散布矩阵 -
k
k
k :簇数,n
n
n:样本总数 CH指数值越大表示聚类分离度高、紧密度好。适合评估不同簇数的选择。
Davies-Bouldin 指数(DB Index)
定义:衡量簇间相似性与簇内散布的比值。
D
B
=
1
k
∑
i
=
1
k
max
j
≠
i
σ
i
+
σ
j
d
(
c
i
,
c
j
)
DB = \\frac{1}{k} \\sum_{i=1}^{k} \\max_{j \\neq i} \\frac{\\sigma_i + \\sigma_j}{d(c_i, c_j)}
DB=k1∑i=1kmaxj=id(ci,cj)σi+σj
-
σ
i
\\sigma_i
σi :簇$ i$内样本的平均距离 -
d
(
c
i
,
c
j
)
d(c_i, c_j)
d(ci,cj) :簇心$i与簇心
与簇心
与簇心j$ 的距离
DB指数的值越小表示簇分离良好,紧密度高。
外部指标(External Metrics)
外部指标依赖真实标签(如果已知),用于比较聚类结果与真实类别的一致性。
归一化互信息(Normalized Mutual Information, NMI)
NMI
(
U
,
V
)
=
2
I
(
U
;
V
)
H
(
U
)
+
H
(
V
)
\\text{NMI}(U,V) = \\frac{2 I(U;V)}{H(U) + H(V)}
NMI(U,V)=H(U)+H(V)2I(U;V)
定义:衡量聚类结果与真实标签之间的信息共享程度,范围 [0, 1],1 表示完全一致。
-
I
(
U
;
V
)
I(U;V)
I(U;V) :互信息 - $ H(U) , H(V)$:聚类与真实标签的熵
特点:对簇数量敏感,能够有效衡量标签一致性。
调整兰德指数(Adjusted Rand Index, ARI)
定义:基于样本对的匹配关系衡量聚类质量,并对随机结果进行了校正。
A
R
I
=
R
I
−
E
[
R
I
]
max
(
R
I
)
−
E
[
R
I
]
ARI = \\frac{RI – E[RI]}{\\max(RI) – E[RI]}
ARI=max(RI)−E[RI]RI−E[RI]
-
R
I
RI
RI :Rand Index - ARI 范围 [-1, 1],1 表示完全一致,0 表示随机聚类效果。
Fowlkes-Mallows 指数(FMI)
定义:基于 TP、FP、FN 计算聚类与真实标签的相似度。
F
M
I
=
T
P
T
P
+
F
P
⋅
T
P
T
P
+
F
N
FMI = \\sqrt{\\frac{TP}{TP+FP} \\cdot \\frac{TP}{TP+FN}}
FMI=TP+FPTP⋅TP+FNTP
- TP:同簇且同类的样本对
- FP:同簇但不同类样本对
- FN:不同簇但同类样本对
FMI值越接近 1 表示聚类与真实标签越一致。
下面我们使用 Iris 数据集进行聚类,计算以上的聚类评估指标
# 导入必要库
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score, calinski_harabasz_score, davies_bouldin_score
from sklearn.metrics import normalized_mutual_info_score, adjusted_rand_score
from sklearn.decomposition import PCA
# 1. 加载 Iris 数据集
iris = load_iris()
X = iris.data
y_true = iris.target # 真实类别
# 2. 数据标准化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# 3. 使用 KMeans 聚类
k = 3 # 聚类簇数
kmeans = KMeans(n_clusters=k, random_state=42)
y_pred = kmeans.fit_predict(X_scaled)
# 4. 计算聚类评估指标
sil_score = silhouette_score(X_scaled, y_pred)
ch_score = calinski_harabasz_score(X_scaled, y_pred)
db_score = davies_bouldin_score(X_scaled, y_pred)
nmi_score = normalized_mutual_info_score(y_true, y_pred)
ari_score = adjusted_rand_score(y_true, y_pred)
print(f"Silhouette Score: {sil_score:.4f}")
print(f"Calinski-Harabasz Index: {ch_score:.4f}")
print(f"Davies-Bouldin Index: {db_score:.4f}")
print(f"NMI (Normalized Mutual Information): {nmi_score:.4f}")
print(f"ARI (Adjusted Rand Index): {ari_score:.4f}")
# 5. 可视化聚类结果(使用 PCA 降到 2D)
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)
plt.figure(figsize=(8,6))
colors = ['red', 'green', 'blue']
for i in range(k):
plt.scatter(X_pca[y_pred==i, 0], X_pca[y_pred==i, 1],
color=colors[i], label=f'Cluster {i}', alpha=0.6, edgecolor='k')
# 标记真实类别中心
plt.xlabel("PCA Component 1")
plt.ylabel("PCA Component 2")
plt.title("KMeans Clustering of Iris Dataset (PCA 2D Visualization)")
plt.legend()
plt.grid(True)
plt.show()
结果如下所示:
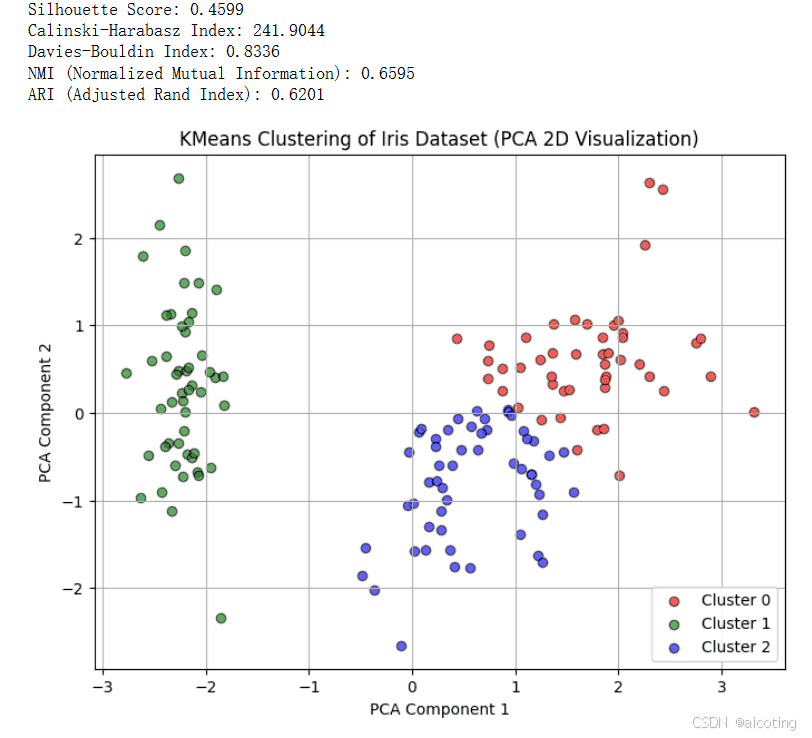
在选择指标的时候,无标签数据使用内部指标如轮廓系数、Calinski-Harabasz、Davies-Bouldin 来评估聚类质量。有标签数据可以使用外部指标 NMI、ARI、FMI,评估聚类结果与真实类别的一致性。
总结一下,聚类评估指标为无监督学习提供了量化工具。从内部指标评估紧密度和分离度,到外部指标衡量与真实标签的一致性,不同指标适用于不同场景。综合使用多种指标可以全面理解聚类效果,帮助选择最佳模型与簇数,从而提升聚类任务的实际应用价值。
最新的文章都在公众号aicoting更新,别忘记关注哦!!!
 网硕互联帮助中心
网硕互联帮助中心
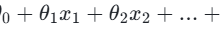



评论前必须登录!
注册