首先说一下为什么要写这一篇博客,就是为了提醒大家要明确区分标准DH和改进DH。很多机器人初学者只知道用DH法建立串联机器人连杆坐标系,然后在看书或者使用DH的时候很糊涂的就模糊了这标准DH和改进DH的区别,最大的坑就是:一些比较老的机器人学教科书用的是标准DH,而现在比较新的机器人书或者说我们大部分用的都是改进DH,这就导致老的教科书里面的一些公式推导和新的网上找的代码不一致,就会比较麻烦。
一:改进DH法
建立连杆坐标系:
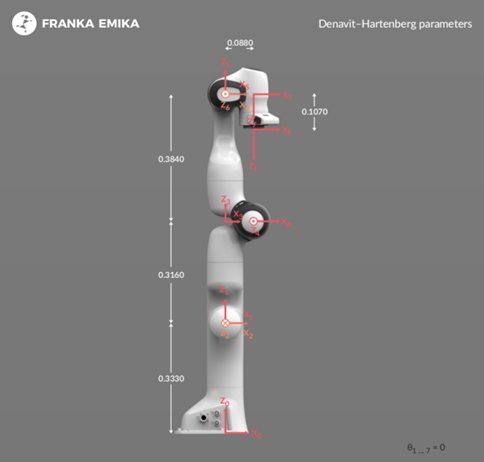
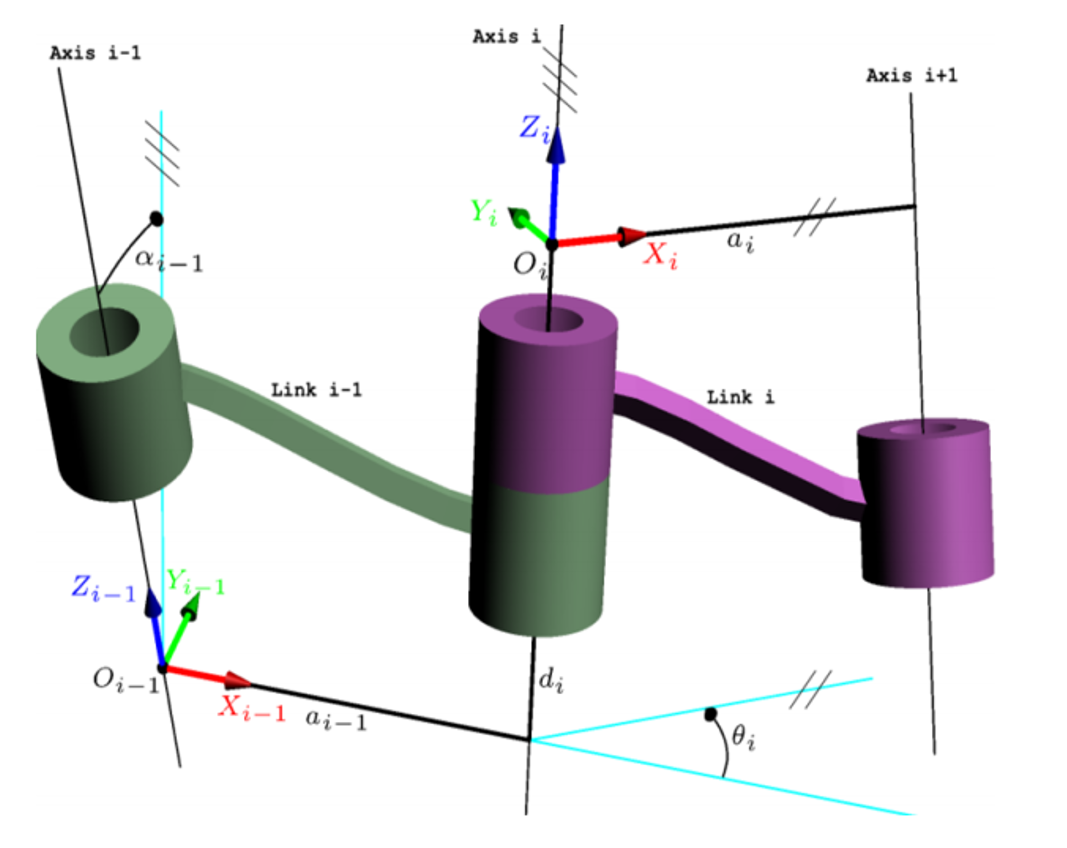
使用改进D-H参数,将![]() 坐标系定义在i
坐标系定义在i![]() 连杆的前端关节:
连杆的前端关节:

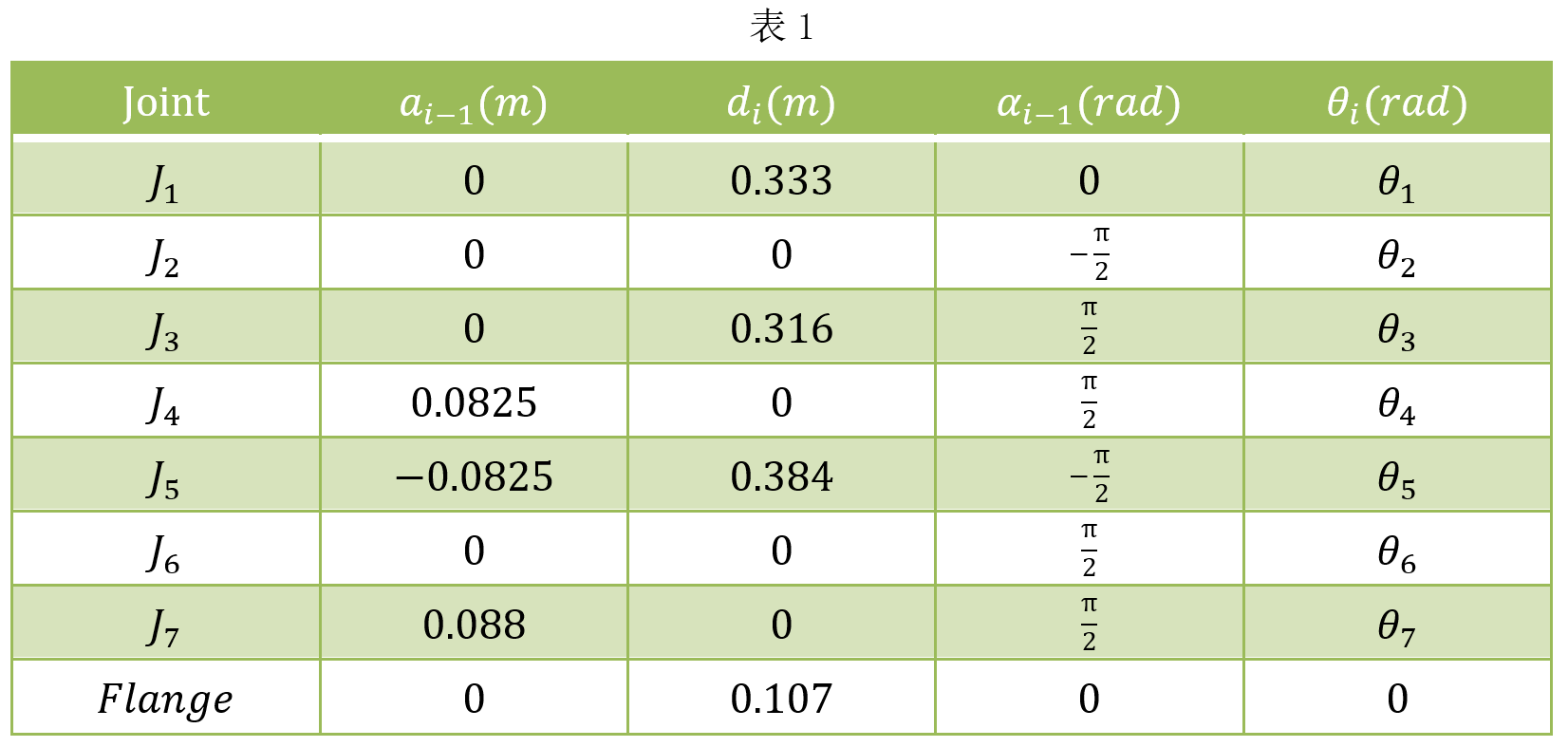

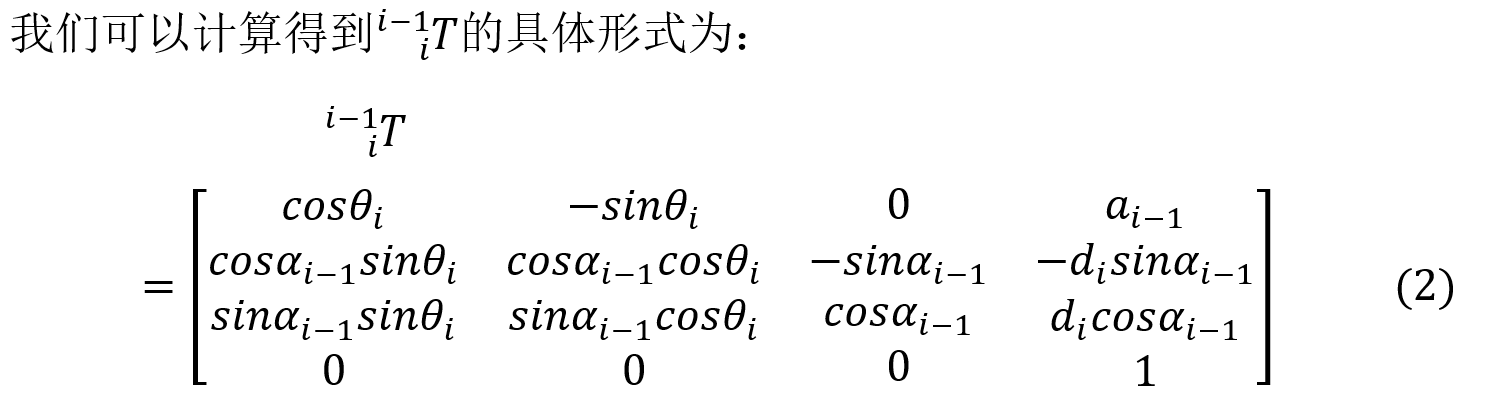


二:标准DH与改进DH法的区别
我们知道一个连杆有两端,一端离基座近,一端离基座远。简单的来说,标准DH将坐标系i建立在连杆i离基座近的一端,改进DH建立在离基座远的一端。
2.1 机器人连杆与关节的标号
先标号,再建系。
连杆编号:基座为杆0,从基座往后依次定义为杆1,杆2,…,杆i;
关节编号:杆i离基座近的一端(近端)的关节为关节i,远的一端(远端)为关节i+1。
为便于理解,这里我把连杆的近端用绿色表示,远端用橙色表示,且远端驱动近端转动。大家只要记住一句话,连杆近端关节的标号和连杆标号是一致的。
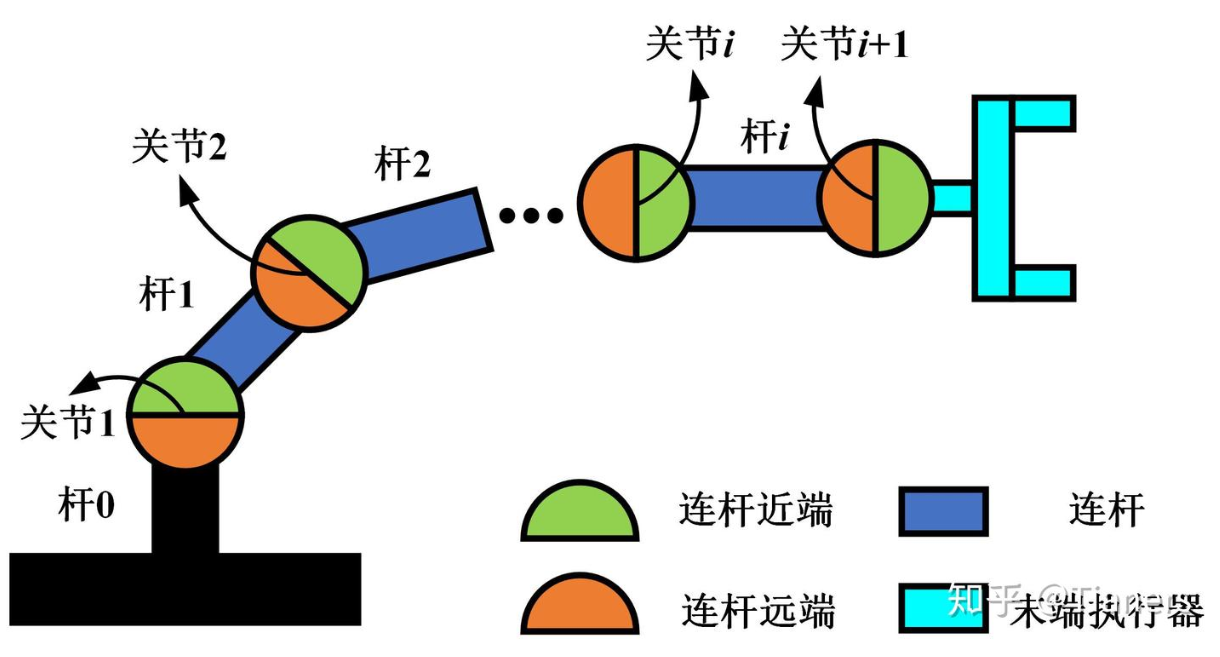
图1连杆和关节标号
2.2 两种建系方法的区别
区别一:连杆坐标系建立的位置不同。SDH方法将连杆i的坐标系固定在连杆的远端,MDH方法把连杆i的坐标系固定在连杆的近端。
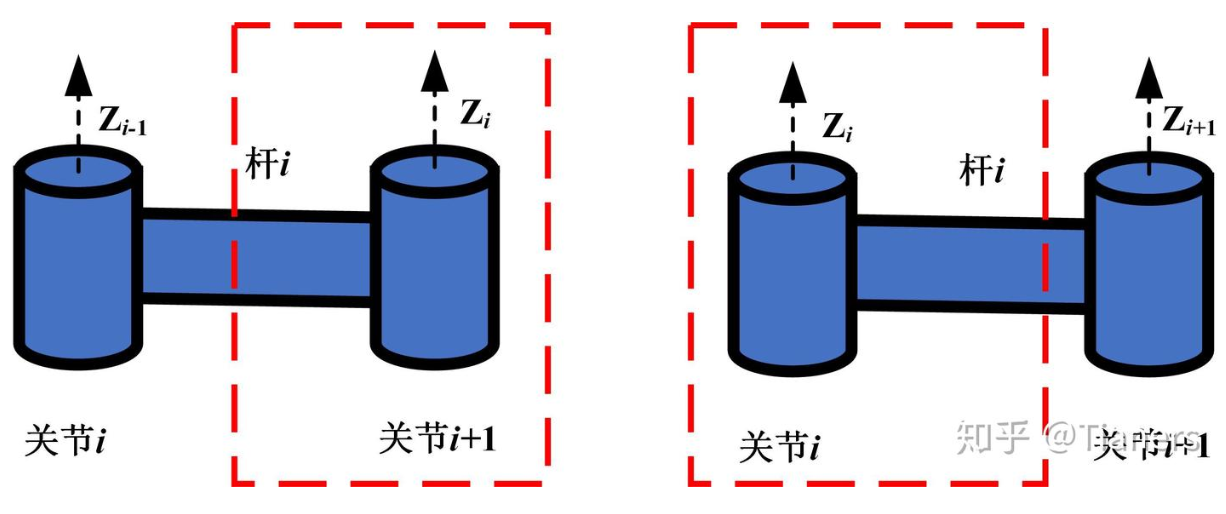
(a)SDH (b)MDH
图2 建系方法的不同
区别二:执行变换的的顺序不同。按照SDH方法变换时四个参数相乘的顺序依次为d—>θ—>a—>α,而MDH方法则按照α—>a—>θ—>d(正好与SDH相反)。
三:为什么要用改进DH法,而不选标准DH法
对于树形结构或者闭链机构的机器人来说,按照SDH方法建立的连杆坐标系会产生歧义,因为SDH的建系原则是把连杆i的坐标系建立在连杆的远端,如图3(a)所示,这就导致连杆0上同时出现了两个坐标系。而MDH把连杆坐标系建立在每个连杆的近端,则不会坐标系重合的情况,如图3(b)所示,这就克服了SDH方法建系的缺点。
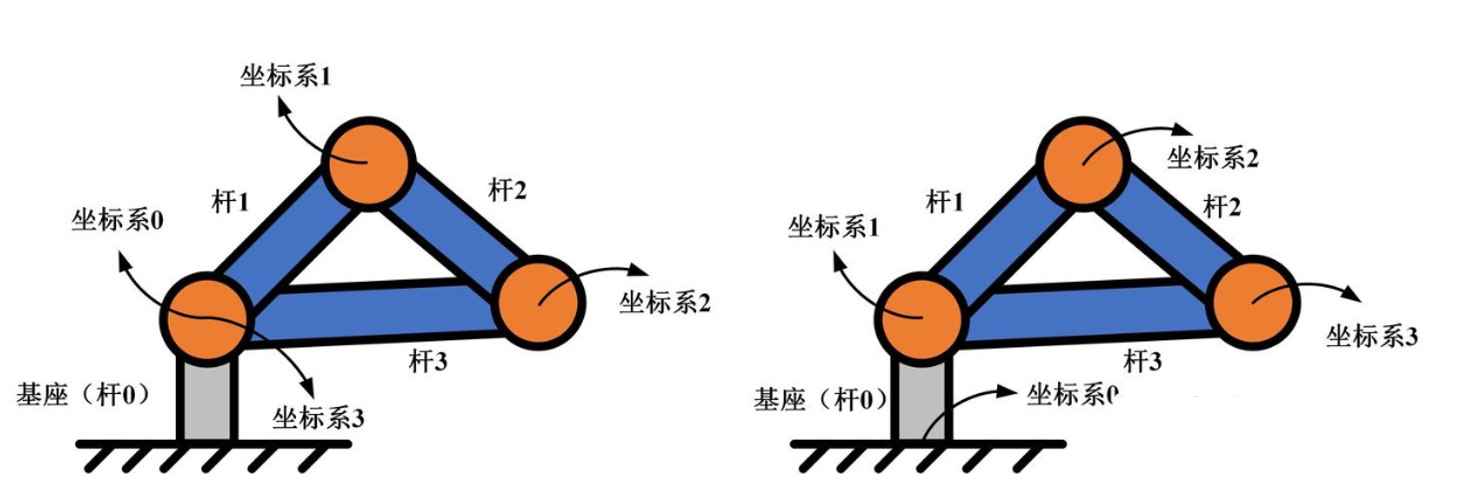
(a)SDH (b)MDH
图3 坐标系分配的不同
四.总结
1.SDH适合应用于开链结构的机器人;
2.当使用SDH表示树状或闭链结构的机器人时,会产生歧义;
3.MDH法对开链、树状、闭链结构的机器人都适用,推荐使用。
五.我遇到的坑
在下面这本教材里面

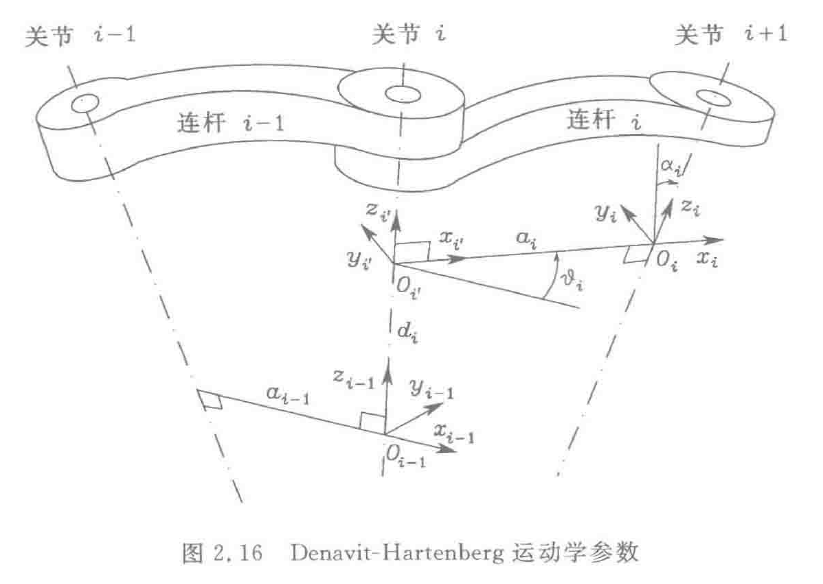
显然用的是DH参数法,因此在后面推导几何雅可比矩阵的时候

提到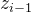 和
和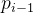 分别由
分别由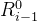 与
与 得到:
得到:

但是如果你用的是改进DH参数法进行建模,核心公式(3.30)应该是:

原因是原本的标准DH的坐标系 对应的z轴
对应的z轴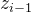 就是改进的DH的的坐标系
就是改进的DH的的坐标系 的z轴
的z轴
下面是基于改进DH计算几何雅可比的代码
function J_geo = geometric_jacobian_from_q_corrected(q)
% 根据关节角度计算几何雅可比矩阵,匹配MATLAB工具箱的顺序
% 输入: q – 7×1关节角向量 (弧度)
% 输出: J_geo – 6×7几何雅可比矩阵
% Franka Panda的DH参数 (Modified DH)
% 格式: [alpha, a, d, theta]
MDH = [0, 0, 0.333, q(1);
-pi/2, 0, 0, q(2);
pi/2, 0, 0.316, q(3);
pi/2, 0.0825, 0, q(4);
-pi/2, -0.0825,0.384, q(5);
pi/2, 0, 0, q(6);
pi/2, 0.088, 0.107, q(7)];
% 计算每个关节的变换矩阵和位置
n = 7;
T = eye(4);
T_all = cell(n, 1);
p_all = zeros(3, n);
z_all = zeros(3, n);
for i = 1:n
alpha = MDH(i, 1);
a = MDH(i, 2);
d = MDH(i, 3);
theta = MDH(i, 4);
% 改进DH变换矩阵
Ti = [cos(theta), -sin(theta), 0, a;
sin(theta)*cos(alpha), cos(theta)*cos(alpha), -sin(alpha), -d*sin(alpha);
sin(theta)*sin(alpha), cos(theta)*sin(alpha), cos(alpha), d*cos(alpha);
0, 0, 0, 1];
T = T * Ti;
T_all{i} = T;
p_all(:, i) = T(1:3, 4);
z_all(:, i) = T(1:3, 3);
end
% 末端执行器位置
p_ee = p_all(:, end);
% 计算几何雅可比 – 修正关节编号对应关系
J_geo = zeros(6, n);
for i = 1:n
if i == 1
% 关节1:使用基坐标系
p_i = [0; 0; 0];
z_i = [0; 0; 1];
else
% 关节i:使用连杆i-1的坐标系
p_i = p_all(:, i); % 改进DH:使用i
z_i = z_all(:, i); % 改进DH:使用i
end
% MATLAB顺序:线速度在前,角速度在后
J_geo(4:6, i) = z_i;
J_geo(1:3, i) = cross(z_i, p_ee – p_i);
end
end
function T = forward_kinematics_mdh(q)
% 改进DH正运动学
MDH = [0, 0, 0.333, q(1);
-pi/2, 0, 0, q(2);
pi/2, 0, 0.316, q(3);
pi/2, 0.0825, 0, q(4);
-pi/2, -0.0825,0.384, q(5);
pi/2, 0, 0, q(6);
pi/2, 0.088, 0.107, q(7)];
T = eye(4);
for i = 1:7
alpha = MDH(i, 1);
a = MDH(i, 2);
d = MDH(i, 3);
theta = MDH(i, 4);
Ti = [cos(theta), -sin(theta), 0, a;
sin(theta)*cos(alpha), cos(theta)*cos(alpha), -sin(alpha), -d*sin(alpha);
sin(theta)*sin(alpha), cos(theta)*sin(alpha), cos(alpha), d*cos(alpha);
0, 0, 0, 1];
T = T * Ti;
end
end
%
 网硕互联帮助中心
网硕互联帮助中心


评论前必须登录!
注册