做 AB 实验分析时,最劝退新人的往往不是复杂的算法,而是那一堆长得像孪生兄弟的基础名词:方差、标准差、标准误差、均方误差……
这几个词在公式里看着都差不多,但在实际业务中,有的用来描述用户,有的用来描述实验,有的用来描述模型。搞混了它们,你的置信区间算不对,显著性结论也是错的。
本文把这些最基础、最容易混淆的统计学概念拎出来,做一个彻底的区分。
1. 方差 (Variance)
定义:
描述数据分布的离散程度。它衡量的是每一个数据点,距离整体平均值的“距离”的平方和的平均值。
数学公式:
σ2=∑(Xi−μ)2N \\sigma^2 = \\frac{\\sum (X_i – \\mu)^2}{N} σ2=N∑(Xi−μ)2
通俗理解:
方差是**“波动的平方”**。
想象你在打靶。如果你的弹孔密密麻麻挤在 10 环周围,方差就很小。如果弹孔散布在整个靶子上,方差就很大。
注意:因为是平方值,单位变了。如果数据是“元”,方差的单位是“元的平方”。这在物理意义上很难解释,所以我们通常更喜欢用标准差。
AB实验用途:
它是所有计算的基石。在计算 T 检验的分母时,第一步永远是先算出两组数据的方差。
深刻解读:
为什么要用“平方和”,而不是直接用“残差和”?
如果你直接计算 (Xi−μ)(X_i – \\mu)(Xi−μ) 的总和,正向偏差(比均值大)和负向偏差(比均值小)会互相抵消,结果永远是 0。这无法反映离散程度。
为什么要用“平方”而不是“绝对值”?
虽然绝对值也能防止抵消,但平方函数是光滑可导的,这在数学推导(如最小二乘法、求极值)上比绝对值方便得多。此外,平方会放大离群值的影响,让模型对极端误差更敏感。
2. 标准差 (Standard Deviation, SD)
定义:
方差的算术平方根。
数学公式:
σ=Variance \\sigma = \\sqrt{\\text{Variance}} σ=Variance
通俗理解:
标准差就是**“平均波动幅度”**。
它的单位和原始数据一致。如果用户人均消费是 100 元,标准差是 20 元,意味着大部分用户的消费在 80 到 120 元之间。
AB实验用途:
主要用于数据探索 (EDA)。
在实验开始前,我们会看一眼数据的标准差,判断这群用户的行为是不是太离散了。如果标准差极大(比如长尾分布),可能需要先做截断(Capping)处理,否则实验很难显著。
深刻解读:
Z 分数 (Z-score) 的原始含义
Z 分数原本是用来衡量**“一个个体”**有多特立独行的。
公式:Z=X−μσZ = \\frac{X – \\mu}{\\sigma}Z=σX−μ (除以标准差)
- 如果 Z = 1.96,说明这个用户处于 Top 2.5% 的极端位置。
- 在正态分布中,均值 ± 1.96个标准差 的范围,覆盖了 95% 的用户个体数据。
- 注意: 这描述的是数据的分布范围,而不是实验结果的可信范围。
3. 标准误差 (Standard Error, SE)
也被简称为标准误,这是最容易和标准差搞混的概念,也是 AB 实验的核心。
定义:
样本均值的抽样分布的标准差。
它衡量的不是“数据”有多散,而是**“如果你重复做实验,算出来的均值”**有多散。
数学公式:
SE=σn SE = \\frac{\\sigma}{\\sqrt{n}} SE=nσ
(标准差除以根号样本量)
通俗理解:
标准差描述的是个体的差异(小明和小王的差距)。
标准误差描述的是实验的精度(这次实验算出的均值,和上帝视角的真实均值之间的差距)。
标准误差,就是样本均值的标准差。
- 样本量 nnn 越大,分母越大,SE 就越小。这意味着实验做得越准,测出的均值越可信。
AB实验用途:
计算置信区间和 P 值。
我们常说的“95% 置信区间”,就是 均值 ± 1.96 * SE。
判断实验显不显著,靠的不是标准差,而是标准误差。
深刻解读:
它来自中心极限定理 (CLT)
中心极限定理告诉我们:不管原始数据长什么样,只要不断抽样算均值,这些**“均值”**组成的分布一定会趋向于正态分布。
而这个“均值分布”的宽度,就是标准误差。
为什么假设检验里用的是 SE而不是标准差(STD)?
在假设检验中,我们计算的 Z 统计量,公式变成了:
Z=Xˉ−μSEZ = \\frac{\\bar{X} – \\mu}{SE}Z=SEXˉ−μ (除以标准误差)
- 这里的 Z,衡量的是**“这次实验的均值”有多特立独行。标准误差,就是样本均值**的标准差。
- 所以,我们常说的 95% 置信区间,公式是 均值 ± 1.96 * SE。
- 关键区别: 标准差 (SD) 决定了用户长什么样;标准误差 (SE) 决定了实验结论准不准。
4. 综合方差 (Pooled Variance)
定义:
当我们要比较两个组(实验组 B 和对照组 A)时,需要把两组的方差“拼”在一起,估算一个整体的波动水平。
数学公式:
Sp2=(nA−1)SA2+(nB−1)SB2nA+nB−2 S_p^2 = \\frac{(n_A-1)S_A^2 + (n_B-1)S_B^2}{n_A + n_B – 2} Sp2=nA+nB−2(nA−1)SA2+(nB−1)SB2
通俗理解:
这就是一个加权平均。
A 组有 A 组的波动,B 组有 B 组的波动。为了做 T 检验,我们需要一个统一的标尺。综合方差就是把两组的波动按样本量加权平均,算出一个“公用”的方差。
AB实验用途:
深刻解读:
什么时候加权?什么时候直接相加?
- 综合方差 (Pooled Variance): 假设两组数据的总体方差是相等的(Homoscedasticity),我们只是为了算得更准,才把它们拼起来加权。这是教科书里标准 T 检验的做法。
- Welch’s T-test(工业界更常用): 在现实业务中,实验组和对照组的方差往往明显不等(比如实验组上了个激进策略,导致用户行为两极分化,方差变大)。此时如果强行加权,P 值会算错。
所以,工业界 AB 实验工具(如 Python 的 ttest_ind(equal_var=False))通常默认使用 Welch 公式。它不计算综合方差,而是直接把两组的标准误平方相加:
SEΔ=SA2nA+SB2nB SE_{\\Delta} = \\sqrt{\\frac{S_A^2}{n_A} + \\frac{S_B^2}{n_B}} SEΔ=nASA2+nBSB2
呐,就是这个公式。 它是计算 T 分数分母最稳健的方法,不管两组方差是否相等,用它都没毛病。 不过注意看:- 分子 S2S^2S2 内部已经除过 n−1n-1n−1 了。
- 外面的分母 nnn 是来自于“均值抽样分布”的中心极限定理(样本量越大,均值越稳)。这个 nnn 代表的是样本数量的缩放效应,不需要减 1。
5. 均方误差 (Mean Squared Error, MSE)
定义:
预测值与真实值之差的平方的期望值。
数学公式:
MSE=1n∑(Yi−Y^i)2 MSE = \\frac{1}{n} \\sum (Y_i – \\hat{Y}_i)^2 MSE=n1∑(Yi−Y^i)2
通俗理解:
这是预测模型的考卷分数。
如果说方差是描述数据自己乱不乱,MSE 就是描述你猜得准不准。
如果你的预测模型(比如 CUPED 里的回归模型)完美预测了每一个点,MSE 就是 0。
AB实验用途:
主要出现在 CUPED (方差缩减) 或 回归分析 中。
CUPED 的核心目标,就是通过引入历史数据,让修正后指标的 MSE(或者说残差的方差)变得最小。
深刻解读:
MSE vs 方差
看公式,MSE 和方差长得非常像,都是“差值的平方和除以 N”。
- 方差减去的是均值(μ\\muμ),它衡量的是数据自身的离散度。
- MSE 减去的是预测值(Y^\\hat{Y}Y^),它衡量的是模型拟合的好坏。
在 AB 实验中,MSE 更多出现在偏机器学习或相关性分析的场景下(如 CUPED 回归、因果推断模型),用来评估我们引入协变量后,到底消除了多少噪音。
6. 总体方差 VS 样本方差
这是统计推断中最基础但也最容易被忽视的区别。
定义区别:
- 总体方差 (σ2\\sigma^2σ2): 上帝视角。假设你能获取全人类的数据,算出来的那个方差。
- 样本方差 (S2S^2S2): 凡人视角。你只抓取了 10 万个用户(样本),算出来的这群人的方差。
AB实验中的现实:
在做 AB 实验时,我们想推断的是“总体”(所有潜在用户)的反应。但我们永远无法知道“总体”的真实方差。
我们手里有的,永远只有“样本方差”。
所以,我们在做假设检验(T-test)时,实际上是用样本方差去代替/估计总体方差。
深刻解读:
为什么样本方差分母是 N-1?(无偏估计与自由度)
当你用样本均值去估算总体均值时,你已经用掉了一个信息量(自由度)。
如果你计算样本方差时分母还用 NNN,算出来的结果会比真实总体方差偏小(有偏估计)。
为了纠正这个偏差,统计学家把分母改成了 N−1N-1N−1。这被称为贝塞尔校正 (Bessel’s Correction)。
这就好比你用一把尺子去量东西,因为尺子本身可能有误差,所以我们故意把读数放大一点点,以确保不会低估真实的波动。
总结:一张表看懂
| 方差 | σ2\\sigma^2σ2 | 数据的波动(平方级) | 数据越集中 | 中间计算过程 |
| 标准差 | σ\\sigmaσ | 数据的波动(原始量级) | 数据越集中 | 看用户画像分布 |
| 标准误差 | SESESE | 均值的测算精度 | 样本量 nnn 越大 | 算 P 值、置信区间 |
| 综合方差 | Sp2S_p^2Sp2 | 两组数据的加权波动 | / | T 检验公式分母、算最小样本量 |
| 均方误差 | MSEMSEMSE | 预测准不准 | 模型越好 | CUPED、回归分析 |
避坑指南:
- 老板问“用户差异大不大”,看标准差。
- 老板问“实验结果准不准”、“显不显著”,看标准误差。
- 做 CUPED 降噪时,关注 MSE。
- 公式里分母是 N−1N-1N−1 时,说明我们在用样本估算总体。
搞清楚这几个“差”,AB 实验的统计学门槛你就跨过去了一半。
 网硕互联帮助中心
网硕互联帮助中心
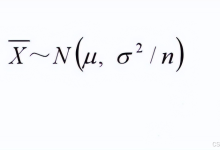



评论前必须登录!
注册