人工智能之数学基础：如何理解事件的独立性？

事件独立的定义

若两事件 A, B 满足P(AB)= P(A) P(B), 则称 A 与 B 相互独立。如果事件A和事件B独立，那么我们可以认为事件A和事件B之间没有任何影响。

事件独立的判断

P(AB)= P(A) P(B)是事件独立的定义，但是在实际应用中，我们需要判断两个事件是否相互影响，如果不相互影响则二者事件独立。

举个例子，一个盒子中有n个小球，从中任取两个，那么此时有两种情况：

有放回的取

这两次取球是相互独立的，第二次抽取的结果不受第一次抽取结果的影响。

无放回的取

这两次取球不是相互独立的，第二次抽取的结果受第一次抽取结果的影响。

事件独立性的定理

证明：

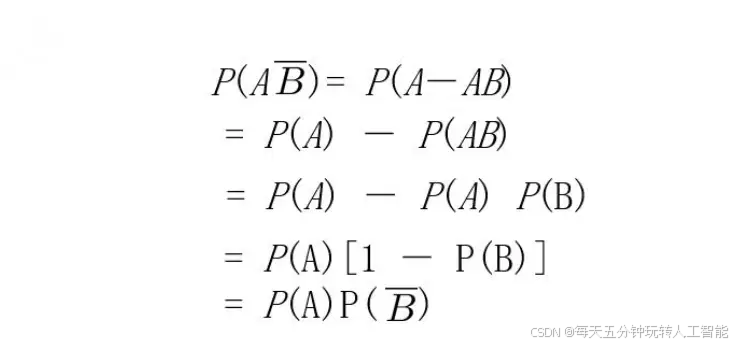
事件独立性的应用

甲乙两射手独立地射击同一目标,他们击中目标的概率分别为0.9和0.8。求每人射击一次后，目标被击中的概率。</