23_VAE如何在潜空间插值?变分推断的概率视角
本章目标:解决 Autoencoder 潜空间不连续的问题。引入 VAE (Variational Autoencoder),让模型学会学习"分布"而不是"点",从而能够生成平滑变化的图像。
目录
1. Autoencoder 的缺陷:潜空间不连续
普通的 Autoencoder 把每张图压缩成这里的一个点。
- 点 A 是"月亮",点 B 是"半月"。
- 但如果你取 A 和 B 的中点 C,解码出来可能是一团乱码。因为网络没见过中间状态。
我们希望潜空间是连续的:从中点采样,应该能生成介于月亮和半月之间的图。
2. VAE 的核心思想:学习分布
VAE 不再让 Encoder 输出一个固定的
z
z
z,而是输出一个高斯分布
N
(
μ
,
σ
2
)
N(\\mu, \\sigma^2)
N(μ,σ2)。
-
μ
\\mu
μ:均值(大概在哪里)。 -
σ
\\sigma
σ:方差(不确定性有多大)。
然后我们从这个分布里随机采样一个
z
z
z,扔给 Decoder。 这就迫使 Decoder 必须对
μ
\\mu
μ 附近的噪点具有鲁棒性,从而填补了潜空间的空隙。
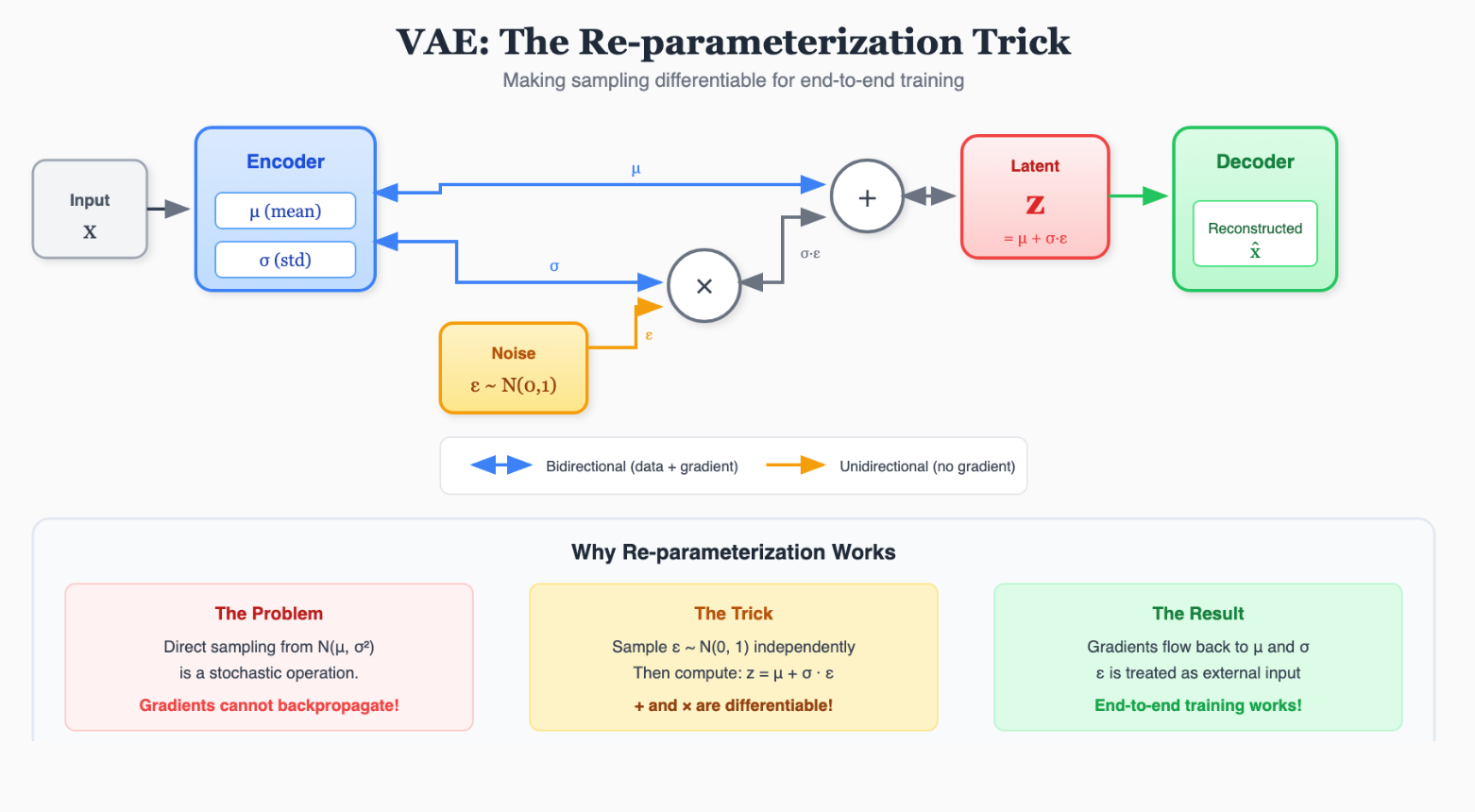
3. 重参数化技巧 (Re-parameterization Trick)
问题来了:"随机采样"这个操作是不可导的! 反向传播会在这里断掉。
解决办法:把随机性剥离出来。 我们需要采样
z
∼
N
(
μ
,
σ
2
)
z \\sim N(\\mu, \\sigma^2)
z∼N(μ,σ2)。 我们可以先采样一个标准正态分布
ϵ
∼
N
(
0
,
1
)
\\epsilon \\sim N(0, 1)
ϵ∼N(0,1)。 然后令:
z
=
μ
+
ϵ
⋅
σ
z = \\mu + \\epsilon \\cdot \\sigma
z=μ+ϵ⋅σ
这样,对于
μ
\\mu
μ 和
σ
\\sigma
σ 来说,操作变成了加法和乘法,完美可导!
4. KL 散度:防止方差为 0
如果只用重建损失,模型会倾向于把
σ
\\sigma
σ 变成 0,退化成普通的 Autoencoder。 我们需要加一个正则项:迫使学到的分布接近标准正态分布
N
(
0
,
1
)
N(0, 1)
N(0,1)。
衡量两个分布差异的指标叫 KL 散度 (Kullback-Leibler Divergence)。
L
o
s
s
=
L
o
s
s
r
e
c
o
n
+
β
⋅
D
K
L
(
N
(
μ
,
σ
2
)
∣
∣
N
(
0
,
1
)
)
Loss = Loss_{recon} + \\beta \\cdot D_{KL}(N(\\mu, \\sigma^2) || N(0, 1))
Loss=Lossrecon+β⋅DKL(N(μ,σ2)∣∣N(0,1))
公式化简后:
D
K
L
=
−
0.5
⋅
∑
(
1
+
ln
(
σ
2
)
−
μ
2
−
σ
2
)
D_{KL} = -0.5 \\cdot \\sum (1 + \\ln(\\sigma^2) – \\mu^2 – \\sigma^2)
DKL=−0.5⋅∑(1+ln(σ2)−μ2−σ2)
5. 实战:PyTorch 实现 VAE 生成手写数字
import torch
import torch.nn as nn
import torch.nn.functional as F
class VAE(nn.Module):
def __init__(self):
super(VAE, self).__init__()
# Encoder
self.fc1 = nn.Linear(784, 400)
self.fc21 = nn.Linear(400, 20) # mu
self.fc22 = nn.Linear(400, 20) # logvar (预测logvar更数值稳定)
# Decoder
self.fc3 = nn.Linear(20, 400)
self.fc4 = nn.Linear(400, 784)
def encode(self, x):
h1 = F.relu(self.fc1(x))
return self.fc21(h1), self.fc22(h1)
def reparameterize(self, mu, logvar):
std = torch.exp(0.5 * logvar)
eps = torch.randn_like(std)
return mu + eps * std # z = mu + eps * std
def decode(self, z):
h3 = F.relu(self.fc3(z))
return torch.sigmoid(self.fc4(h3))
def forward(self, x):
mu, logvar = self.encode(x.view(–1, 784))
z = self.reparameterize(mu, logvar)
return self.decode(z), mu, logvar
# Loss Function
def loss_function(recon_x, x, mu, logvar):
BCE = F.binary_cross_entropy(recon_x, x.view(–1, 784), reduction='sum')
# KL Divergence Formula
KLD = –0.5 * torch.sum(1 + logvar – mu.pow(2) – logvar.exp())
return BCE + KLD
下一章预告: VAE 生成的图片总是有点模糊(因为 Loss 是算像素均方差)。有没有办法让生成的图片极其逼真,连毛孔都清晰可见? 我们需要两个网络互相打架 —— GAN (生成对抗网络)。
下一章:24_GAN的博弈如何达到纳什均衡?生成对抗网络原理
 网硕互联帮助中心
网硕互联帮助中心




评论前必须登录!
注册