多机器人路径规划的多策略自适应差分正余弦算法，Multi-robot path planning多机器人路径规划。附代码

1、简介

最近进行了使用各种元启发式算法进行多机器人路径规划的研究。其中一种算法正弦余弦算法（SCA）不能在路径规划问题中产生令人满意的结果，由于单一的更新策略。有必要采用多种更新策略，并针对更广泛的问题提高其性能。我们提出了一种新的多策略自适应微分正弦余弦算法（sdSCA），它使用策略池，并允许更频繁地选择策略，从而导致更好的解决方案，将sdSCA应用于具有静态和动态障碍物的复杂环境中的在线多机器人路径规划。

2、基本正弦余弦算法(SCA)

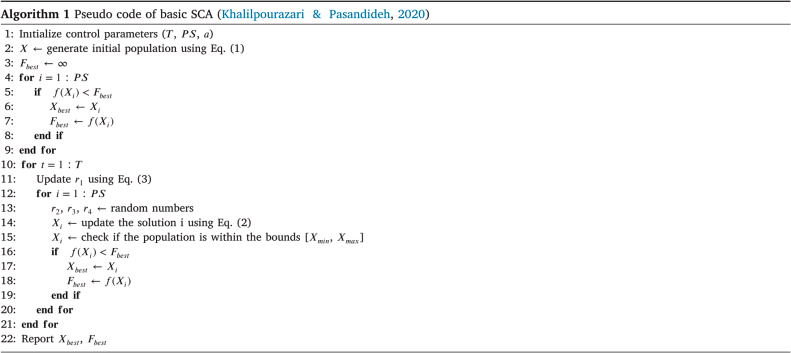
SCA是Mirjalili于2016年提出的基于数学的先进元启发式算法。该算法在更新解时采用正弦和余弦函数构建的方程，这些三角函数能有效利用两个不同解之间的空间(Mirjalili, 2016)。算法流程如下：首先通过式(1)随机生成初始种群：

$$X_i=X_{min}+(X_{max}-X_{min})rand(1,D),i\in \{1,2,\dots ,PS\}\text{\hspace{1em}(1)}$$

其中$X_i$表示候选解$i$，$X_{min}$和$X_{max}$分别表示解的上下界，$D$和$PS$分别代表问题维度和种群规模。种群经适应度函数评估后开始迭代过程，解通过式(2)更新：

$$X_i^{t+1}=\{\begin{array}{ll}{X}_i^t+r_1\sin (r_2)|r_3{X}_{best}^t-X_i^t|& \text{如果 }{r}_4<0.5\\ X_i^t+r_1\cos (r_2)|r_3{X}_{best}^t-X_i^t|& \text{否则}\end{array}\text{\hspace{1em}(2)}$$

式中$X_i^{t+1}$表示第$t+1$代候选解$i$，$X_i^t$为第$t$代候选解$i$，$X_{best}^t$是第$t$代种群中的最优解。$r_1$通过式(3)计算：

$$r_1=a-t\frac{a}{T}\text{\hspace{1em}(3)}$$

其中$t$为当前迭代次数，$T$为最大迭代次数，$a$为常数。$r_2$、$r_3$和$r_4$分别为[0,2π]、[0,2]和[0,1]范围内的随机数。新种群经适应度函数评估后继续迭代直至满足停止条件，最终输出最优解。最小化问题的SCA伪代码见算法1。

3、多策略自适应差分正弦余弦算法(sdSCA)

基于种群的元启发式算法首先生成随机初始种群，经适应度函数评估后开始迭代更新过程。多数算法中，种群候选解通常采用单一更新策略，迭代结束时输出最优解。然而单一更新策略会限制算法搜索性能。SCA作为基于种群的算法，其原始更新策略如式(2)所示。为突破这一限制，本文在SCA原有策略基础上引入差分策略，提出新型多策略自适应差分正弦余弦算法(sdSCA)。该算法中，每个候选解通过轮盘赌概率计算自主选择更新策略（非随机选择），算法自适应学习产生更优结果的策略，从而提升基础SCA的搜索性能。所提算法在基础SCA更新方程外新增三种差分策略，分别如式(4)、式(5)和式(6)所示：

$$X_i^{t+1}=\{\begin{array}{ll}{X}_{R_1}^t+F\left(X_{R_2}^t-X_{R_3}^t\right)& \text{若}rand<CR\\ X_i^t& \text{否则}\end{array}\text{\hspace{1em}(4)}$$

$$X_i^{t+1}=\{\begin{array}{ll}{X}_i^t+F\left(X_{best}^t-X_i^t+X_{R_1}^t-X_{R_2}^t\right)& \text{若}rand<CR\\ X_i^t& \text{否则}\end{array}\text{\hspace{1em}(5)}$$

$$X_i^{t+1}=X_i^t+L\left(X_{R_1}^t-X_i^t\right)+F\left(X_{R_2}^t-X_{R_3}^t\right)\text{\hspace{1em}(6)}$$

其中$X_{R_1}^t$、$X_{R_2}^t$和$X_{R_3}^t$为第$t$代随机选取的三个候选解，$F$为缩放因子，$L$为[0,1]范围内的随机数，$CR$为交叉率。

算法流程说明：首先由式(2)、(4)-(6)构建包含四种差分策略的策略池，初始阶段各策略选择概率均设为25%。通过式(1)随机生成初始种群后，各候选解采用轮盘赌技术选择策略。经适应度函数评估后开始迭代，候选解按各自策略更新，同时更新策略选择计数器。新种群评估后，按式(7)计算各策略更新概率：

$$p_k^{t+1}=\frac{c_k^t}{{\sum }_{i=1}^{NS}{c}_i},k\in \{1,2,\dots ,NS\}\text{\hspace{1em}(7)}$$

式中$p_k^{t+1}$表示第$t+1$代策略$k$的选择概率，$c_k^t$为第$t$代策略$k$的计数器，$NS$为策略总数。基于更新概率，候选解再次通过轮盘赌调整策略选择，直至满足停止条件。最小化问题的sdSCA流程图见算法2和图2。

4、多机器人在线路径规划建模

多机器人在线路径规划是一个最小化问题，旨在使机器人在复杂环境中逐步到达目标点，同时以最小成本避免与静态/动态障碍物及其他机器人碰撞(Toufan & Nitzade, 2020)。本文针对圆形同构多机器人系统进行在线路径规划仿真，机器人下一位置可通过式(8)-(9)计算：

$$x_i^n=x_i^c+v_i\cos \left({\theta }_i\right)\text{\hspace{1em}(8)}$$
$$y_i^n=y_i^c+v_i\sin \left({\theta }_i\right)\text{\hspace{1em}(9)}$$

其中$(x_i^n,y_i^n)$表示机器人$i$的下一位置坐标，$(x_i^c,y_i^c)$为当前位置坐标，$v_i$和${\theta }_i$分别为机器人$i$的速度和角度。速度定义为单步移动距离，通过每步优化确定机器人下一位置，该优化基于所有机器人的速度和角度参数。首先在速度范围$[v_{min},v_{max}]$和角度范围$[{\theta }_{min},{\theta }_{max}]$内创建局部搜索空间，然后确定该空间中最可行下一位置的速度和角度。机器人持续移动至目标点，所有机器人的速度和角度作为整体进行优化。由于优化基于这两个运动特性，问题维度$D$与机器人数量$N^R$成正比，即$D=N^R\times 2$。主适应度函数如式(10)所示：

KaTeX parse error: Invalid delimiter type 'ordgroup' at position 61: …_{i}\\right)\\big{̲|̲}̲i\\in \\left\\{1,\\…

主适应度函数评估以下四个准则：

• $F_1$: 最短路径；$F_2$: 避让静态障碍物；$F_3$: 避让动态障碍物 ； $F_4$: 避让其他机器人

各子函数数学表达如下：

4.1 最短路径函数

$$F_1=\sum _{i=1}^{N^R}\left(f_i+g_i\right)\text{\hspace{1em}(11)}$$
其中：
$$f_i=\sqrt{{\left(x_i^n-x_i^c\right)}^2+{\left(y_i^n-y_i^c\right)}^2}\text{\hspace{1em}(12)}$$
$$g_i=\sqrt{{\left(x_i^g-x_i^n\right)}^2+{\left(y_i^g-y_i^n\right)}^2}\text{\hspace{1em}(13)}$$
$(x_i^g,y_i^g)$为机器人$i$的目标坐标。

4.2 静态避障函数

$$F_2=\{\begin{array}{ll}c& \text{若 }{d}_i^s\le d_i^{safe}\\ 0& \text{若 }{d}_i^s>d_i^{safe}\end{array}\text{\hspace{1em}(14)}$$
其中$c\in {\mathbb{R}}^{+}$为大数惩罚项，$d_i^s$为机器人$i$到所有静态障碍物的距离和：
$$d_i^s=\sum _{j=1}^{N^s}\sqrt{{\left(x_i^n-x_j^s\right)}^2+{\left(y_i^n-y_j^s\right)}^2}\text{\hspace{1em}(15)}$$
$N^s$为静态障碍物数量，$(x_j^s,y_j^s)$为静态障碍物$j$的坐标。

4.3 动态避障函数\\

$$F_3=\{\begin{array}{ll}c& \text{若 }{d}_i^d\le d_i^{safe}\\ 0& \text{若 }{d}_i^d>d_i^{safe}\end{array}\text{\hspace{1em}(16)}$$
动态障碍物距离和：
$$d_i^d=\sum _{j=1}^{N^d}\sqrt{{\left(x_i^n-x_j^d\right)}^2+{\left(y_i^n-y_j^d\right)}^2}\text{\hspace{1em}(17)}$$

4.4 机器人避碰函数

$$F_4=\{\begin{array}{ll}c& \text{若 }{d}_i^r\le d_i^{safe}\\ 0& \text{若 }{d}_i^r>d_i^{safe}\end{array}\text{\hspace{1em}(18)}$$
机器人间距离和：
$$d_i^r=\sum _{j=1,j\ne i}^{N^R}\sqrt{{\left(x_i^n-x_j^c\right)}^2+{\left(y_i^n-y_j^c\right)}^2}\text{\hspace{1em}(19)}$$

总适应度函数为各子函数之和：
$$Fit=F_1+F_2+F_3+F_4\text{\hspace{1em}(20)}$$

动态障碍物运动模型由式(21)-(22)描述：
$$x_j^d=x_j^d+v_j^d\cos \left({\alpha }_j\right)\text{\hspace{1em}(21)}$$
$$y_j^d=y_j^d+v_j^d\sin \left({\alpha }_j\right)\text{\hspace{1em}(22)}$$
其中$v_j^d$为动态障碍物$j$的速度，${\alpha }_j$为其相对于目标点的角度。路径规划算法伪代码见算法3。

5、算法性能评估指标

本文通过步数、移动距离、路径偏差误差、未达目标距离、总适应度和执行时间等指标评估算法性能。下面对路径偏差误差和未达目标距离进行详细说明。

5.1 平均路径偏差误差(APDE)

在迭代开始前，路径规划算法会为每个机器人计算数学上的理想路径（起点到目标的直线）。路径偏差误差(PDE)指算法实际路径与理想路径的距离差，第$k$次运行的PDE计算如式(23)：

$$PD{E}_k=\sum _{i=1}^{N^R}\left(T{D}_i^k-I{D}_i\right)\text{\hspace{1em}(23)}$$

其中$T{D}_i^k$表示第$k$次运行时机器人$i$的实际移动距离，$I{D}_i$为机器人$i$的理想路径距离。平均路径偏差误差(APDE)计算如式(24)，$R$为总运行次数：

$$APDE=\frac{1}{R}\sum _{k=1}^{R}PD{E}_k\text{\hspace{1em}(24)}$$

5.2 平均未达目标距离(AUGD)

当步数最多的机器人到达目标点时算法终止运行。在此过程中记录每个机器人每步到目标点的距离，欧氏距离计算如式(25)：

Hij,k=∥Pij,k−Gi∥(25)H_{i}^{j,k}=\\left\\|P_{i}^{j,k}-G_{i}\\right\\| \\tag{25}Hij,k​=​Pij,k​−Gi​​(25)

其中$H_i^{j,k}$表示第$k$次运行第$j$步时机器人$i$到目标的距离，$P_i^{j,k}$为优化得到的新位置，$G_i$为目标点坐标。第$k$次运行的未达目标距离$(UG{D}_k)$计算如式(26)：

$$UG{D}_k=\sum _{j=1}^{MS}\sum _{i=1}^{N^R}{H}_i^{j,k}\text{\hspace{1em}(26)}$$

$MS$为最大步数机器人的总步数。平均未达目标距离(AUGD)计算如式(27)：

$$AUGD=\frac{1}{R}\sum _{k=1}^{R}UG{D}_k\text{\hspace{1em}(27)}$$

6、多机器人路径规划求解算法

提出的算法被应用于多机器人在线路径规划。仿真中机器人均为圆形、同构且尺寸统一，动态障碍物以恒定速度在两特定点间线性移动。研究构建了三个包含静态和动态障碍物的场景（单位：厘米）：

参数设置：

• 机器人半径：$1$ cm
• 动态障碍物半径：$1.5$ cm
• 优化参数范围：
  速度 $v\in [1,1.5]$ cm/步
  角度 $\theta \in [0,2\pi ]$ rad
• 适应度函数$F_2$、$F_3$和$F_4$的惩罚系数：$c=10^5$

动态障碍物的速度设计旨在限制机器人运动并增加问题复杂度。各场景中机器人理想路径用彩色虚线表示，目标点用同色十字标记；动态障碍物路径用黑色点划线表示，目标点用黑色方框标记。

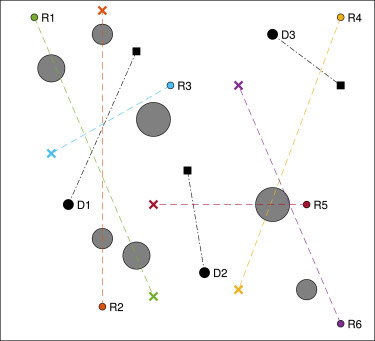
图1 场景1

% data of scenario 1
% ===================================================================
totalRobot = 6; % number of robot
robotRadius = ones(1, totalRobot); % radius of robot
robotStart.x = [5 25 45 95 85 95]; % start positions (x) of robots
robotStart.y = [95 10 75 95 40 5]; % start positions (y) of robots
robotGoal.x = [40 25 10 65 40 65]; % goal positions (x) of robots
robotGoal.y = [13 97 55 15 40 75]; % goal positions (y) of robots
totalStatic = 7; % number of static obstacles
staticRadius = [4 3 3 5 4 5 3]; % radius of static obstacles
static.x = [10 25 25 40 35 75 85]; % positions (x) of static obstacles
static.y = [80 90 30 65 25 40 15]; % positions (y) of static obstacles
totalDynamic = 3; % number of dynamic obstacles
dynamicRadius = 1.5 * ones(1, totalDynamic); % radius of dynamic obstacles
dynamicStart.x = [15 55 75]; % start positions (x) of dynamic obstacles
dynamicStart.y = [40 20 90]; % start positions (y) of dynamic obstacles
dynamicGoal.x = [35 50 95]; % goal positions (x) of dynamic obstacles
dynamicGoal.y = [85 50 75]; % goal positions (y) of dynamic obstacles
dynamicVelocity = [0.5 0.45 1.2]; % velocities of dynamic obstacles
axisParameter = 100; % visualization scale (100 x 100)
% ===================================================================
% initial visualization
% ===================================================================
figure
alpha = linspace(0, 2*pi, 100);
set(gcf, 'Position', [500, 20, 950, 950]);
ax = gca;
ax.Units = 'normalized';
ax.Position = [0.05 0 0.9 1];
plt1 = plot(–7,–7,'o','MarkerFaceColor',[0.5 0.5 0.5],'MarkerEdgeColor','k','MarkerSize',12);
hold on;
plt2 = plot(–8,–8,'o','MarkerFaceColor',[0.5 0.7 0.8],'MarkerEdgeColor','k','MarkerSize',12);
plt3 = plot(–9,–9,'o','MarkerFaceColor',[0.1 0.2 0.9],'MarkerEdgeColor','k','MarkerSize',12);
for i = 1 : totalStatic
if i == 2 || i == 4
x_square = [static.x(i) – staticRadius(i), static.x(i) + staticRadius(i), static.x(i) + staticRadius(i), static.x(i) – staticRadius(i)];
y_square = [static.y(i) – staticRadius(i), static.y(i) – staticRadius(i), static.y(i) + staticRadius(i), static.y(i) + staticRadius(i)];
plt10 = fill(x_square, y_square, [0.5 0.5 0.5]);
elseif i == 3 || i == 5
x_tri = [static.x(i), static.x(i) – staticRadius(i) * sqrt(3) / 2, static.x(i) + staticRadius(i) * sqrt(3) / 2, static.x(i)];
y_tri = [static.y(i) + staticRadius(i), static.y(i) – staticRadius(i) / 2, static.y(i) – staticRadius(i) / 2, static.y(i) + staticRadius(i)];
plt10 = fill(x_tri, y_tri, [0.5 0.5 0.5]);
else
plt10 = fill(static.x(i) + staticRadius(i) * cos(alpha), static.y(i) + staticRadius(i) * sin(alpha), [0.5 0.5 0.5]);
end
end
for i = 1 : totalRobot
plt11(i) = fill(robotStart.x(i) + robotRadius(i) * cos(alpha), robotStart.y(i) + robotRadius(i) * sin(alpha), [0.5 0.7 0.8]);
plt4 = plot(robotGoal.x(i), robotGoal.y(i),'x','MarkerFaceColor','k','MarkerEdgeColor','k','MarkerSize',10,'LineWidth',2);
plt5 = line([robotStart.x(i) robotGoal.x(i)], [robotStart.y(i) robotGoal.y(i)],'Color','black','LineStyle','–');
end
for i = 1 : totalDynamic
plt12(i) = fill(dynamicStart.x(i) + dynamicRadius(i) * cos(alpha), dynamicStart.y(i) + dynamicRadius(i) * sin(alpha), [0.1 0.2 0.9]);
plt6 = plot(dynamicGoal.x(i), dynamicGoal.y(i),'x','MarkerFaceColor','b','MarkerEdgeColor','b','MarkerSize',10,'LineWidth',2);
plt7 = line([dynamicStart.x(i) dynamicGoal.x(i)], [dynamicStart.y(i) dynamicGoal.y(i)],'Color','blue','LineStyle','–');
end
legend([plt2 plt1 plt3], {'(6) Robots','(7) Static obstacles', '(3) Dynamic obstacles'},'FontSize',14,'Location','north');
axis equal;
axis([–5 (axisParameter+5) 0 (axisParameter)]);
pause(1);
% ===================================================================
saveas(gcf,'scenario\\scenario1.emf');

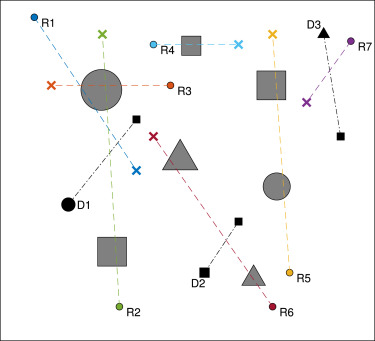
图2 场景2

% data of scenario 2
% ===================================================================
totalRobot = 12; % number of robot
robotRadius = ones(1, totalRobot); % radius of robot
robotStart.x = [8 13 29 34 39 50 60 60 60 66 97 97]; % start positions (x) of robots
robotStart.y = [31 11 78 31 89 63 31 84 94 63 42 86]; % start positions (y) of robots
robotGoal.x = [18 13 29 18 39 76 102 81 87 34 97 97]; % goal positions (x) of robots
robotGoal.y = [47 90 16 31 47 26 58 94 73 5 79 94]; % goal positions (y) of robots
totalStatic = 9; % number of static obstacles
staticRadius = [2 2 1 3 2 2 3 2 4]; % radius of static obstacles
static.x = [13 25 34 29 29 58 85 68 13]; % positions (x) of static obstacles
static.y = [40 31 31 45 65 50 47 88 70]; % positions (y) of static obstacles
totalDynamic = 5; % number of dynamic obstacles
dynamicRadius = 1.5 * ones(1, totalDynamic); % radius of dynamic obstacles
dynamicStart.x = [40 24 34 66 92]; % start positions (x) of dynamic obstacles
dynamicStart.y = [40 47 84 26 63]; % start positions (y) of dynamic obstacles
dynamicGoal.x = [60 34 45 76 100]; % goal positions (x) of dynamic obstacles
dynamicGoal.y = [15 68 63 52 65]; % goal positions (y) of dynamic obstacles
dynamicVelocity = rand(1,totalDynamic) + 0.2; % velocities of dynamic obstacles
axisParameter = 100; % visualization scale (100 x 100)
% ===================================================================
% initial visualization
% ===================================================================
figure
alpha = linspace(0, 2*pi, 100);
set(gcf, 'Position', [500, 20, 950, 950]);
ax = gca;
ax.Units = 'normalized';
ax.Position = [0.05 0 0.9 1];
plt1 = plot(–7,–7,'o','MarkerFaceColor',[0.5 0.5 0.5],'MarkerEdgeColor','k','MarkerSize',12);
hold on;
plt2 = plot(–8,–8,'o','MarkerFaceColor',[0.5 0.7 0.8],'MarkerEdgeColor','k','MarkerSize',12);
plt3 = plot(–9,–9,'o','MarkerFaceColor',[0.1 0.2 0.9],'MarkerEdgeColor','k','MarkerSize',12);
for i = 1 : totalStatic
if i == 2 || i == 5 || i == 7
x_square = [static.x(i) – staticRadius(i), static.x(i) + staticRadius(i), static.x(i) + staticRadius(i), static.x(i) – staticRadius(i)];
y_square = [static.y(i) – staticRadius(i), static.y(i) – staticRadius(i), static.y(i) + staticRadius(i), static.y(i) + staticRadius(i)];
plt10 = fill(x_square, y_square, [0.5 0.5 0.5]);
elseif i == 3 || i == 5 || i == 8
x_tri = [static.x(i), static.x(i) – staticRadius(i) * sqrt(3) / 2, static.x(i) + staticRadius(i) * sqrt(3) / 2, static.x(i)];
y_tri = [static.y(i) + staticRadius(i), static.y(i) – staticRadius(i) / 2, static.y(i) – staticRadius(i) / 2, static.y(i) + staticRadius(i)];
plt10 = fill(x_tri, y_tri, [0.5 0.5 0.5]);
else
plt10 = fill(static.x(i) + staticRadius(i) * cos(alpha), static.y(i) + staticRadius(i) * sin(alpha), [0.5 0.5 0.5]);
end
end
for i = 1 : totalRobot
plt11(i) = fill(robotStart.x(i) + robotRadius(i) * cos(alpha), robotStart.y(i) + robotRadius(i) * sin(alpha), [0.5 0.7 0.8]);
plt4 = plot(robotGoal.x(i), robotGoal.y(i),'x','MarkerFaceColor','k','MarkerEdgeColor','k','MarkerSize',10,'LineWidth',2);
plt5 = line([robotStart.x(i) robotGoal.x(i)], [robotStart.y(i) robotGoal.y(i)],'Color','black','LineStyle','–');
end
for i = 1 : totalDynamic
plt12(i) = fill(dynamicStart.x(i) + dynamicRadius(i) * cos(alpha), dynamicStart.y(i) + dynamicRadius(i) * sin(alpha), [0.1 0.2 0.9]);
plt6 = plot(dynamicGoal.x(i), dynamicGoal.y(i),'x','MarkerFaceColor','b','MarkerEdgeColor','b','MarkerSize',10,'LineWidth',2);
plt7 = line([dynamicStart.x(i) dynamicGoal.x(i)], [dynamicStart.y(i) dynamicGoal.y(i)],'Color','blue','LineStyle','–');
end
legend([plt2 plt1 plt3], {'(12) Robots', '(9) Static obstacles', '(5) Dynamic obstacles'},'FontSize',14,'Location','southeast');
axis equal;
axis([–5 (axisParameter+5) 0 (axisParameter)]);
pause(1);
% ===================================================================
saveas(gcf,'scenario\\scenario2.emf');

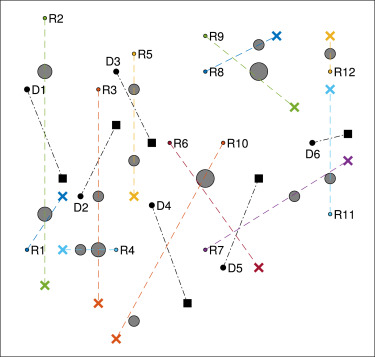
图3 场景3

% data of scenario 3
% ===================================================================
totalRobot = 20; % number of robot
robotRadius = ones(1, totalRobot); % radius of robot
robotStart.x = [5 5 25 25 10 85 40 60 45 72 60 105 145 145 145 100 100 50 100 120] ; % start positions (x) of robots
robotStart.y = [135 100 5 100 5 85 40 80 45 72 60 130 145 110 80 20 125 15 100 25]; % start positions (y) of robots
robotGoal.x = [25 25 5 75 15 40 70 80 5 120 90 120 145 145 145 125 125 75 130 140]; % goal positions (x) of robots
robotGoal.y = [135 125 25 125 85 125 140 80 70 72 30 110 120 90 30 60 125 15 80 25]; % goal positions (y) of robots
totalStatic = 13; % number of static obstacles
staticRadius = [5 3 5 4 3 3 3 3 4 4 5 5 3]; % radius of static obstacles
static.x = [12 100 43 55 30 110 50 145 145 145 145 115 107]; % positions (x) of static obstacles
static.y = [45 72 60 90 55 120 70 50 65 100 130 90 32]; % positions (y) of static obstacles
totalDynamic = 7; % number of dynamic obstacles
dynamicRadius = 1.5 * ones(1, totalDynamic); % radius of dynamic obstacles
dynamicStart.x = [15 50 30 60 17 100 75]; % start positions (x) of dynamic obstacles
dynamicStart.y = [145 140 80 30 5 60 55] ; % start positions (y) of dynamic obstacles
dynamicGoal.x = [15 70 60 63 25 135 60]; % goal positions (x) of dynamic obstacles
dynamicGoal.y = [100 70 75 5 15 40 40]; % goal positions (y) of dynamic obstacles
dynamicVelocity = rand(1,totalDynamic) + 0.2; % velocities of dynamic obstacles
axisParameter = 150; % visualization scale (150 x 150)
% ===================================================================
% Robots path's colors
% ===================================================================
Colors = jet(totalRobot);
% Colors = (Colors+[1 1 1])./2;
% ===================================================================
% initial visualization
% ===================================================================
figure
alpha = linspace(0, 2*pi, 150);
set(gcf, 'Position', [500, 20, 950, 950]);
ax = gca;
ax.Units = 'normalized';
ax.Position = [0.05 0 0.9 1];
plt1 = plot(–7,–7,'o','MarkerFaceColor',[0.5 0.5 0.5],'MarkerEdgeColor','k','MarkerSize',12);
hold on;
plt2 = plot(–8,–8,'o','MarkerFaceColor',[0.5 0.7 0.8],'MarkerEdgeColor','k','MarkerSize',12);
plt3 = plot(–9,–9,'o','MarkerFaceColor',[0.1 0.2 0.9],'MarkerEdgeColor','k','MarkerSize',12);
for i = 1 : totalStatic
if i == 2 || i == 7 || i == 10 || i == 13 || i == 17
x_square = [static.x(i) – staticRadius(i), static.x(i) + staticRadius(i), static.x(i) + staticRadius(i), static.x(i) – staticRadius(i)];
y_square = [static.y(i) – staticRadius(i), static.y(i) – staticRadius(i), static.y(i) + staticRadius(i), static.y(i) + staticRadius(i)];
plt10 = fill(x_square, y_square, [0.5 0.5 0.5]);
elseif i == 3 || i == 8 || i == 11 || i == 14 || i == 18
x_tri = [static.x(i), static.x(i) – staticRadius(i) * sqrt(3) / 2, static.x(i) + staticRadius(i) * sqrt(3) / 2, static.x(i)];
y_tri = [static.y(i) + staticRadius(i), static.y(i) – staticRadius(i) / 2, static.y(i) – staticRadius(i) / 2, static.y(i) + staticRadius(i)];
plt10 = fill(x_tri, y_tri, [0.5 0.5 0.5]);
else
plt10 = fill(static.x(i) + staticRadius(i) * cos(alpha), static.y(i) + staticRadius(i) * sin(alpha), [0.5 0.5 0.5]);
end
end
for i = 1 : totalRobot
plt11(i) = fill(robotStart.x(i) + robotRadius(i) * cos(alpha), robotStart.y(i) + robotRadius(i) * sin(alpha), [0.5 0.7 0.8]);
plt4 = plot(robotGoal.x(i), robotGoal.y(i),'x','MarkerFaceColor','k','MarkerEdgeColor','k','MarkerSize',10,'LineWidth',2);
plt5 = line([robotStart.x(i) robotGoal.x(i)], [robotStart.y(i) robotGoal.y(i)],'Color','black','LineStyle','–');
end
for i = 1 : totalDynamic
plt12(i) = fill(dynamicStart.x(i) + dynamicRadius(i) * cos(alpha), dynamicStart.y(i) + dynamicRadius(i) * sin(alpha), [0.1 0.2 0.9]);
plt6 = plot(dynamicGoal.x(i), dynamicGoal.y(i),'x','MarkerFaceColor','b','MarkerEdgeColor','b','MarkerSize',10,'LineWidth',2);
plt7 = line([dynamicStart.x(i) dynamicGoal.x(i)], [dynamicStart.y(i) dynamicGoal.y(i)],'Color','blue','LineStyle','–');
end
legend([plt2 plt1 plt3], {'(20) Robots', '(13) Static obstacles', '(7) Dynamic obstacles'},'FontSize',14,'Location','southeast');
axis equal;
axis([–5 (axisParameter+5) 0 (axisParameter)]);
pause(1);
% ===================================================================
saveas(gcf,'scenario\\scenario3.emf');

6.1 实验结果

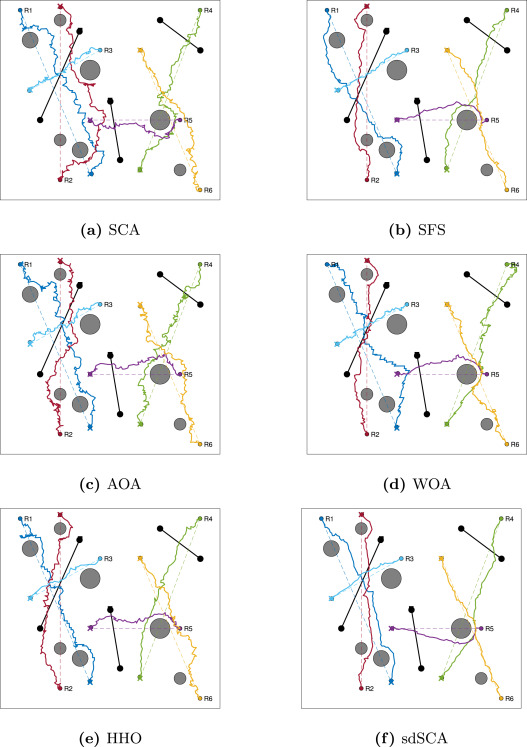
图9.场景1中算法获得的示例路径

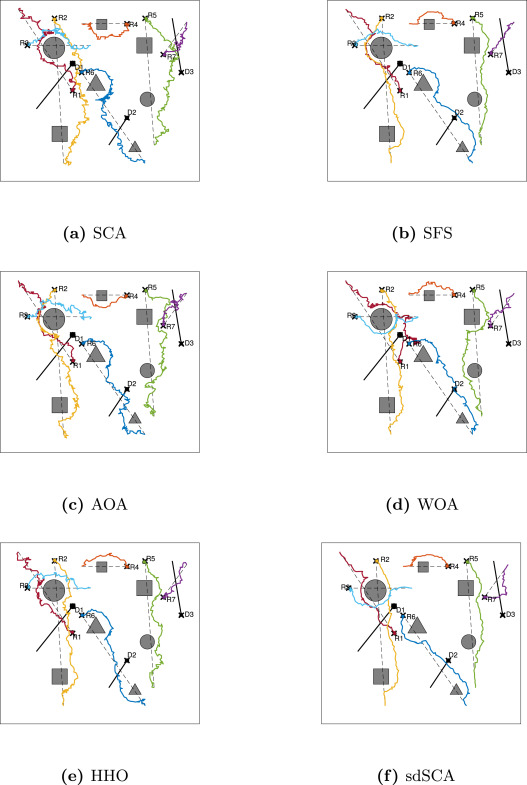
图10.场景2中算法获得的示例路径

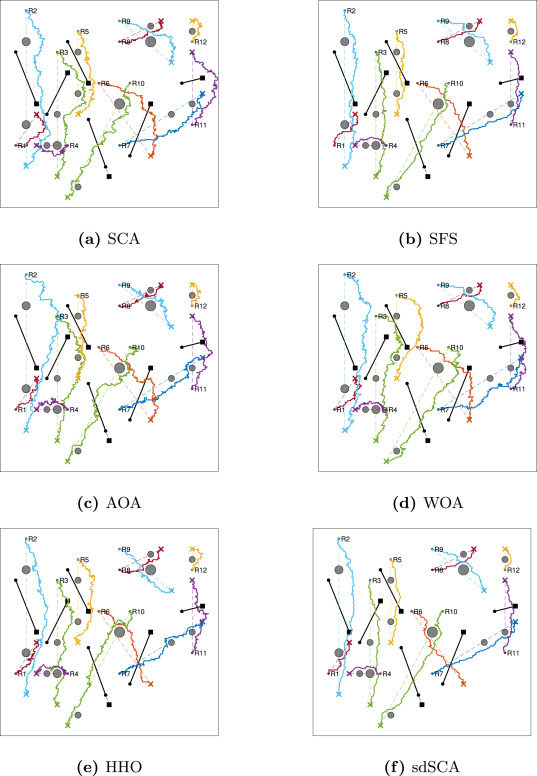
图11.场景3中算法获得的示例路径

【1】Albay Rustem, Yildirim Mustafa Yusuf. Multi-strategy and self-adaptive differential sine–cosine algorithm for multi-robot path planning[J]. Expert Systems with Applications, 2023, 232: 120849.

【2】Zhu, Lun, et al. “Self-adaptive differential evolution-based coati optimization algorithm for multi-robot path planning.” Robotica (2025): 1-38.