本文为个人学习总结,如有谬误欢迎指正。密码学博大精深,后续将继续记录其他知识点!
目录
前言
一、介绍
二、加密流程⚠️
扩展置换E
S盒替换
置换P
完整计算案例
三、安全性分析
存在互补密钥
密钥长度过短 (56位):
理论攻击方法:
四、变形:2-DES 与 3-DES
2-DES (Double DES):
中间相遇攻击
攻击复杂度分析
3-DES (Triple DES):
3DES能抵抗中间相遇攻击?
总结
前言
在信息安全领域,对称密码算法扮演着核心角色。其中,分组密码因其对固定长度数据块(分组)进行独立加解密的特性而被广泛应用。而DES(Data Encryption Standard)作为历史上最具影响力的分组密码之一,其精巧的Feistel结构设计至今仍是密码学教学的经典范例。
一、介绍
- 对称密码(加解密使用一个密钥)
- 分组密码
- Feistel结构(迭代16轮,加解密结构相同,只是密钥顺序相反)
参数:
明密文分组:
- 处理的数据块(明文/密文分组)固定为64位;按比特(左右分成32bit)
密钥分组:
-
初始密钥长度:64位。
-
有效密钥长度:56位(其中8位用于奇偶校验)。
-
每轮实际使用的子密钥长度:48位(由56位主密钥经过一系列置换和压缩生成)
迭代次数:
- 数据块经历16轮完全相同的处理流程,每一轮都使用不同的48位子密钥
二、加密流程⚠️
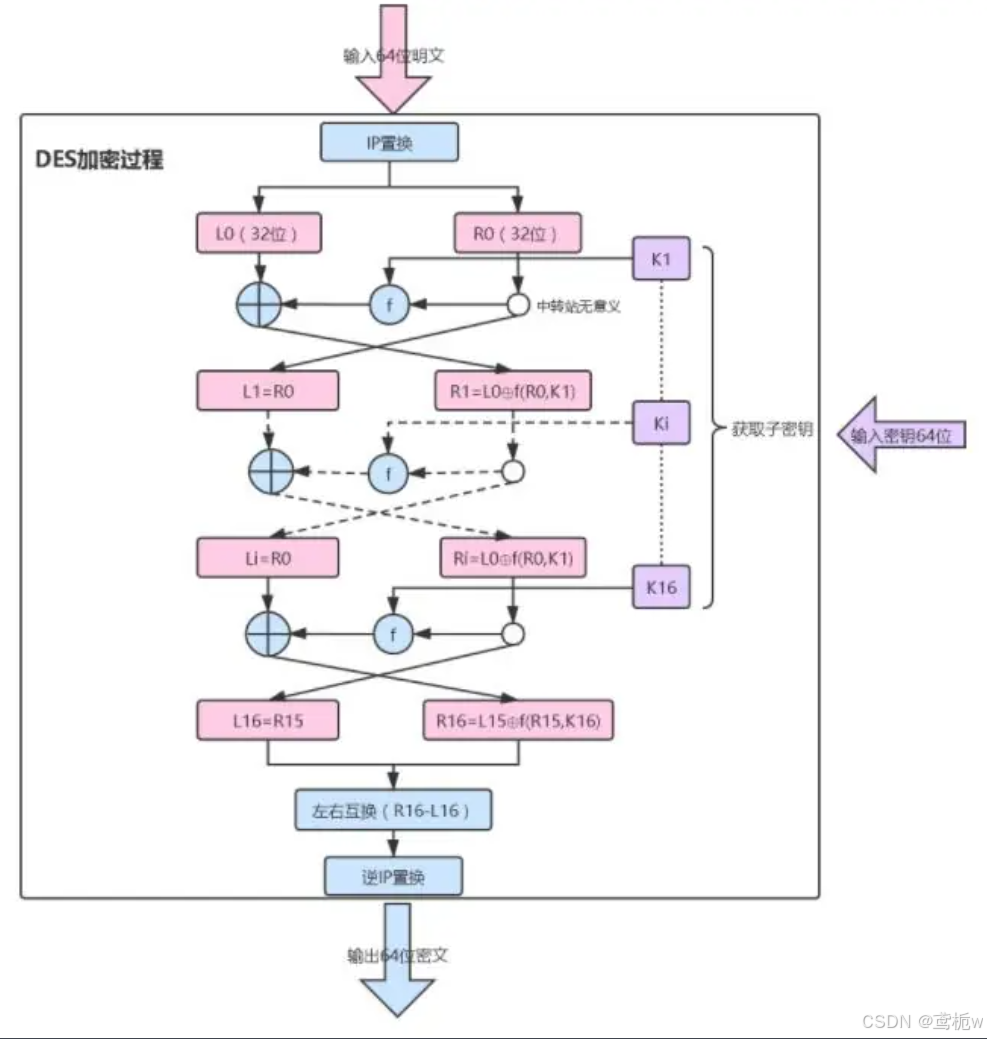
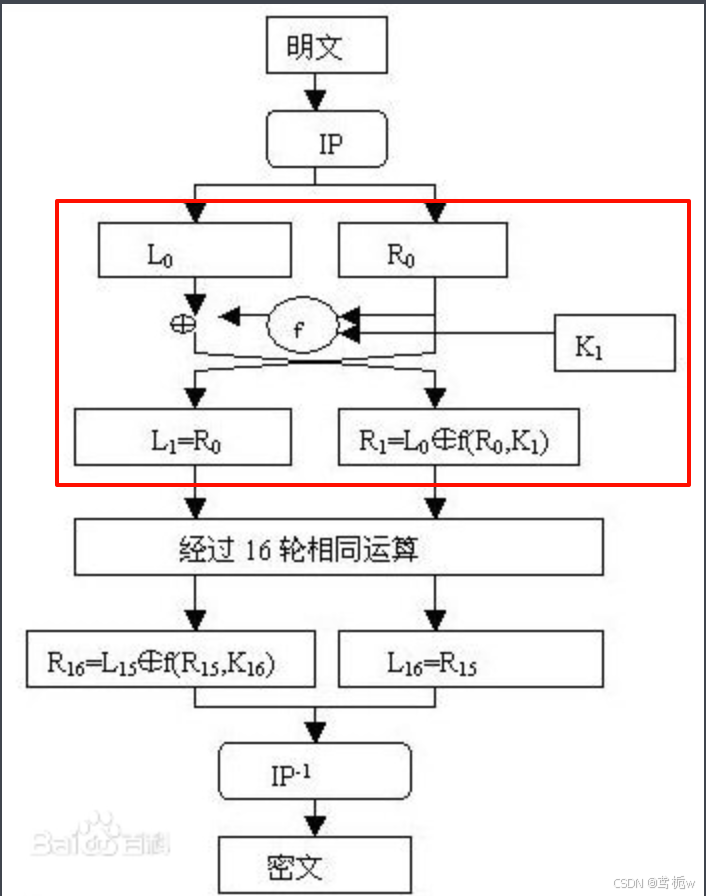
明文分组:
- 每组64bit
初始置换 (IP):
- 输入的64位明文首先通过一个固定的初始置换矩阵 (IP) 进行比特重排。
16轮Feistel迭代:
-
拆分:将置换后的64位数据分成左右两半:左半部分 (L₀, 32位) 和 右半部分 (R₀, 32位)。
-
轮函数 F 处理 (核心):
-
扩展置换 (E): 将32位的 Rᵢ₋₁ 扩展为48位(通过重复某些比特实现)。
-
子密钥混合 (XOR): 将扩展后的48位结果与当前轮的48位子密钥 Kᵢ 进行异或 (XOR) 运算。
-
S盒替换 (Substitution): 将48位结果分成8组6位数据,每组输入一个不同的6输入4输出S盒 (S-Box)。每个S盒执行关键的非线性替换,输出4位。此步将48位数据压缩回32位。
-
置换 (P): 将S盒输出的32位结果通过一个固定的置换矩阵 (P) 进行比特重排。输出即为轮函数 F(Rᵢ₋₁, Kᵢ) 的结果(32位)。
-
合并与交换:
-
新的左半部分:Lᵢ = Rᵢ₋₁
-
新的右半部分:Rᵢ = Lᵢ₋₁ XOR F(Rᵢ₋₁, Kᵢ)
-
-
重复:以上步骤重复执行16轮。
最终处理:
-
交换合并:16轮迭代后,交换最后得到的 L₁₆ 和 R₁₆(即输出 R₁₆ || L₁₆,共64位)。
-
逆初始置换 (IP⁻¹):将交换合并后的64位数据通过逆初始置换矩阵 (IP⁻¹) 进行比特重排。
-
输出:得到最终的64位密文分组。
关键点:DES的解密流程与加密流程完全一致,唯一区别是子密钥的使用顺序为 K₁₆, K₁₅, …, K₁。
扩展置换E
-
将32位数据划分为8个4位块
-
每个4位块扩展为6位:[b1 b2 b3 b4] → [b4 b1 b2 b3 b4 b1]
-
关键特性:首位和末位重复(实现输入比特的扩散)
扩展表
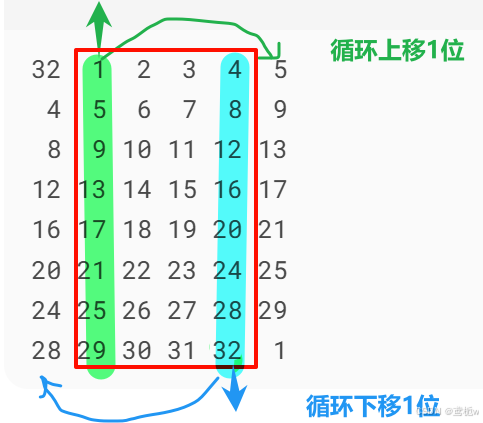

S盒替换
-
将48位输入分为8组6位数据
-
每组输入独立的S盒(S1-S8)
-
每个S盒是4×16的查找表(6位输入 → 4位输出)
S盒查找规则:
取6位输入:b1 b2 b3 b4 b5 b6
行号 = (b1 b6)₂ (0-3)
列号 = (b2 b3 b4 b5)₂ (0-15)
输出 = S盒[行号][列号](4位)
以S1为例:

输入6位: 101101 行号 = (11)₂ = 3 列号 = (0110)₂ = 6 查S1[3][6] = 7 → 二进制 0111
置换P
-
输出位i = 输入位P[i](按表位置映射)
-
例:输出第1位 = 输入第16位
-
输出第2位 = 输入第7位
-
…
-
输出第32位 = 输入第25位
置换表
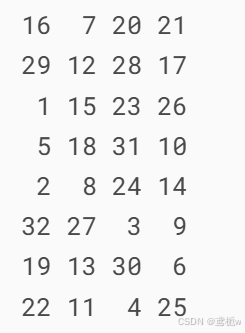
输入32位: 0001 0010 0011 0100 0101 0110 0111 1000 置换后: 位1 ← 位16 (0) 位2 ← 位7 (1) 位3 ← 位20 (0) … 位32 ← 位25 (1) 输出:1000 1110 0010 1101 0101 0010 1010 0101
完整计算案例
计算步骤:
E扩展:
输入32位:1100 1010 1111 0000 0011 0101 1001 0110
扩展48位:011000 010111 111100 000001 001101 010110 101001 101100
与子密钥异或:
扩展后:011000 010111 111100 000001 001101 010110 101001 101100
Kᵢ: 010110 101001 011010 110100 001011 110101 100110 111000
异或结果:001110 111110 100110 110101 000110 100011 001111 010100
S盒替换:
分组:001110 111110 100110 110101 000110 100011 001111 010100
S1(001110):行=00(0), 列=0111(7) → 13(1101)
S2(111110):行=10(2), 列=1111(15) → 0(0000)
…(其他S盒类似)
输出32位:1101 0000 1001 0110 1110 1011 0010 1000
P置换:
输入32位:1101 0000 1001 0110 1110 1011 0010 1000
置换后:1010 1110 0001 1100 0010 1101 1000 0110(最终F函数输出)
三、安全性分析
存在互补密钥
安全影响:可将穷举密钥搜索空间减少一半(攻击者只需尝试一半密钥即可验证两个可能结果)。虽然实际攻击价值有限,但它揭示了DES结构的内在数学性质。
这也是des的一个重要数学性质,称为互补特性或取反特性:
-
如果使用密钥 K 加密明文 P 得到密文 C。
-
那么使用密钥 K'(即 K 的逐位取反)加密明文 P'(即 P 的逐位取反),得到的密文将是 C'(即 C 的逐位取反)。
-
公式表示:DESₖ'(P') = (DESₖ(P))'
密钥长度过短 (56位):
-
密钥空间仅有 2⁵⁶ ≈ 7.2 × 10¹⁶ 种可能。
-
现代计算能力(如GPU、专用硬件)可在数小时甚至更短时间内完成穷举攻击(暴力破解)。1998年的DES挑战赛首次被公开破解即是明证。
理论攻击方法:
-
差分密码分析 (Differential Cryptanalysis):通过分析特定明文差分对对应密文差分的影响来恢复密钥。DES的S盒设计在一定程度上抵抗了这种当时未知的攻击。
-
线性密码分析 (Linear Cryptanalysis):寻找明文、密文和密钥比特之间的概率线性逼近关系来恢复密钥。比差分分析更有效,也是现代重要的分析手段。
四、变形:2-DES 与 3-DES
为克服DES密钥过短的问题,发展出多重DES方案
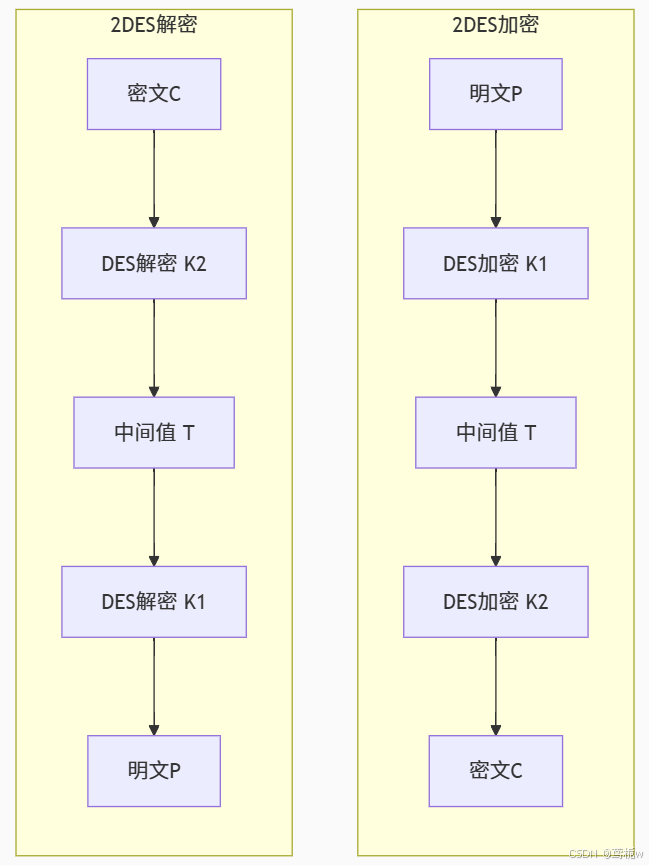
2-DES (Double DES):
使用两个密钥,2次加密
-
加密:C = E(K₂, E(K₁, P))
-
解密:P = D(K₁, D(K₂, C))
-
密钥长度:112位(2 × 56位)。
-
致命缺陷:易受中间相遇攻击 (Meet-in-the-Middle Attack)。攻击者通过预计算和存储 E(K₁, P) 与 D(K₂, C) 的中间结果进行匹配,可将有效攻击复杂度降至约 2⁵⁷,安全性仅略高于单DES,不推荐使用。
中间相遇攻击
C = E(K₂, E(K₁, P)) 可转化为:E(K₁, P) = D(K₂, C)
攻击者通过双向计算并匹配中间值,将攻击复杂度从理论上的2¹¹²大幅降至2⁵⁷。
攻击步骤(需1组已知明文-密文对(P, C))
1.正向计算(加密方向):
- 枚举所有2⁵⁶个可能的K₁
- 对每个K₁计算:T = E(K₁, P)
- 存储结果:建立(T, K₁)的查找表(空间复杂度2⁵⁶)
2.逆向计算(解密方向):
- 枚举所有2⁵⁶个可能的K₂
- 对每个K₂计算:S = D(K₂, C)
- 在查找表中搜索匹配的T值(满足T = S)
3.密钥验证:
- 对每个匹配的(K₁, K₂)候选对
- 用新明文-密文对验证是否正确
- 若验证成功,则获得正确密钥
攻击复杂度分析
| 理论穷举攻击 | 2¹¹² | 极小 | 112位 |
| 中间相遇攻击 | 2⁵⁷ | 2⁵⁶ | 仅57位 |
| 单DES攻击 | 2⁵⁵ | 极小 | 55位 |
空间代价:存储2⁵⁶条记录约需15,000 TB(56位密钥+64位中间值),现代分布式系统可实现。
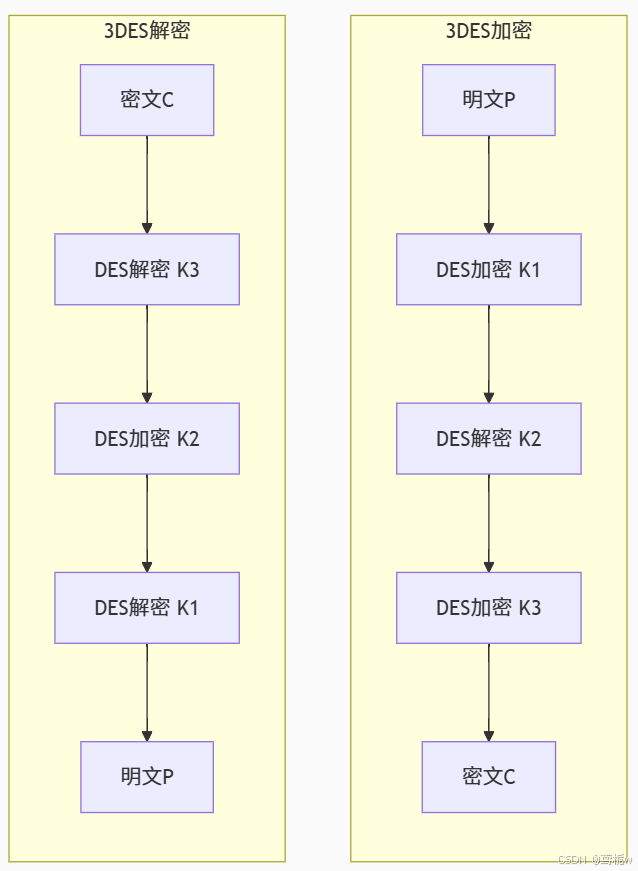
3-DES (Triple DES):
-
常用加密模式 (EDE):
-
C = E(K₃, D(K₂, E(K₁, P)))(加密)
-
P = D(K₁, E(K₂, D(K₃, C)))(解密)
-
-
密钥选项:
-
三密钥 (Keying Option 1):K₁, K₂, K₃ 独立(共168位)。安全性最高。
-
双密钥 (Keying Option 2):K₁ = K₃(共112位)。常用且安全。
-
-
优点:
-
充分利用现有DES硬件/软件实现。
-
密钥长度(112或168位)足以抵抗穷举攻击。
-
经过充分分析和标准化(如ANSI X9.52, NIST SP 800-67),安全性得到广泛认可。
-
-
缺点:速度比DES慢约3倍,比AES慢更多。
3DES能抵抗中间相遇攻击?
3DES的EDE结构(加密-解密-加密)通过三重操作阻断中间值匹配:
C = E(K₃, D(K₂, E(K₁, P)))
攻击者需同时破解三层密钥:
正向攻击需处理:D(K₂, E(K₁, P)) = D(K₃, C)
逆向攻击需处理:E(K₁, P) = E(K₂, D(K₃, C))
无法建立直接等式关系,攻击复杂度恢复至理论值:
- 双密钥3DES:2¹¹²
- 三密钥3DES:2¹⁶⁸
注:虽然存在三重DES的中间相遇攻击变种,但复杂度高达2¹¹²(双密钥)或2¹⁶⁸(三密钥),实际不可行。
总结
附上本文思维导图
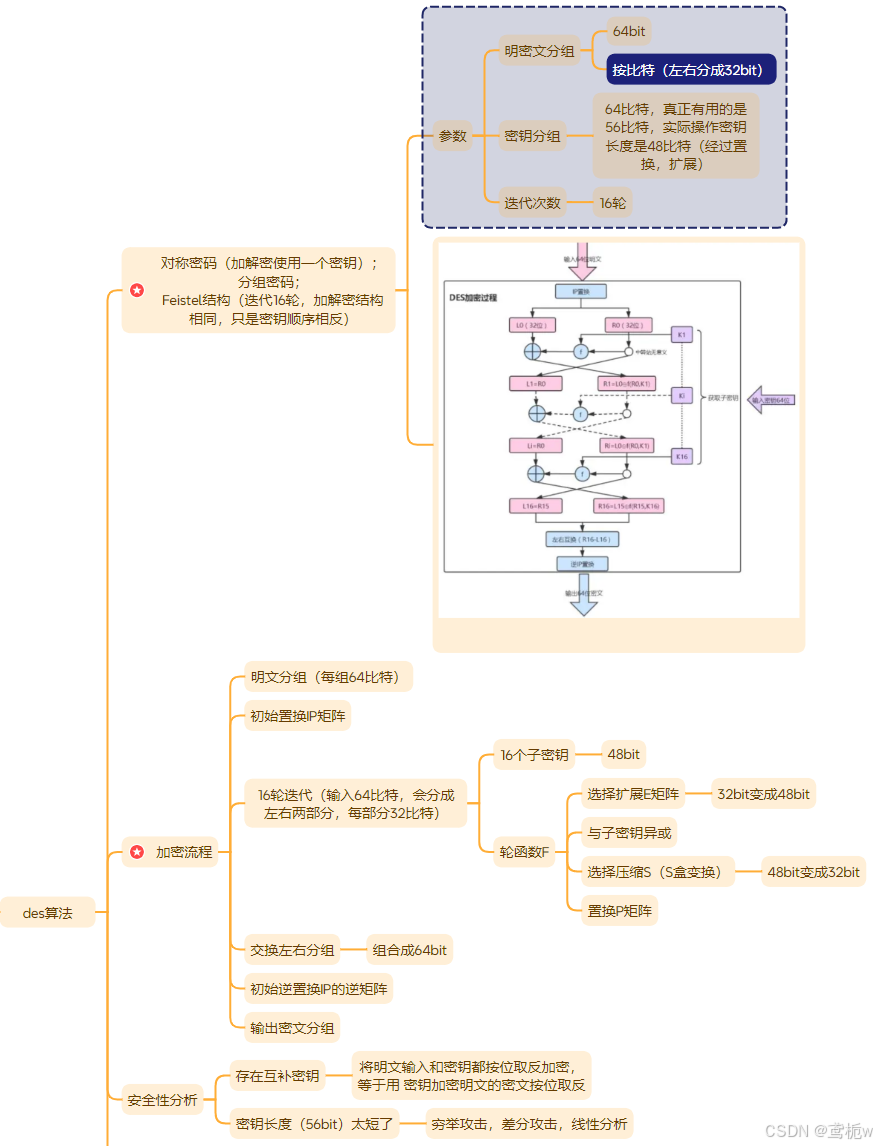
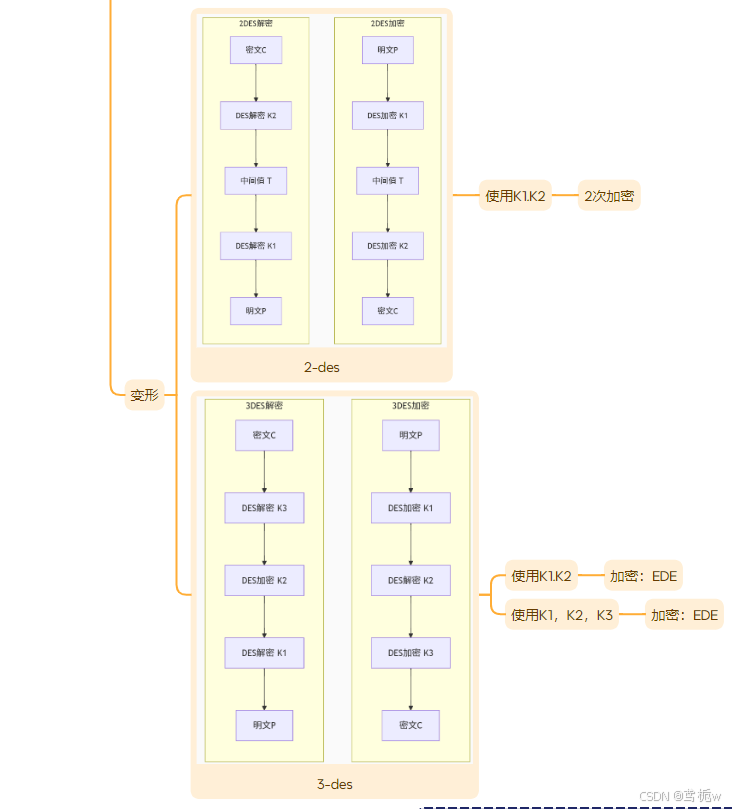
注:部分图片源自百度
 网硕互联帮助中心
网硕互联帮助中心



评论前必须登录!
注册