从冒泡到快速排序：探索经典排序算法的奥秘（二）

引入

哈喽大家好，我是野生的编程萌新，首先感谢大家的观看。数据结构的学习者大多有这样的想法：数据结构很重要，一定要学好，但数据结构比较抽象，有些算法理解起来很困难，学的很累。我想让大家知道的是：数据结构非常有趣，很多算法是智慧的结晶，我希望大家在学习数据结构的过程是一种愉悦的心情感受。因此我开创了《数据结构》专栏，在这里我将把数据结构内容以有趣易懂的方式展现给大家。

1.选择排序

1.1引入

假设你有一个杂乱无章的书架，上面放着一些书籍。你想要按照书名的字母顺序来整理这些书籍。你可以使用选择排序的方法来完成这个任务。首先，你站在书架前，从左到右依次查看每一本书的书名。你的目标是找到书名字母顺序最靠前的那本书。例如，如果你的书架上有以下几本书：

• 《Moby Dick》
• 《War and Peace》
• 《Don Quixote》
• 《Crime and Punishment》
• 《Anna Karenina》

你会依次查看这些书的书名，发现《Anna Karenina》是字母顺序最靠前的那本书。然后，你将这本书从原来的位置上取下来，放到书架的第一个位置上。接下来，你在剩下的书籍中找到书名字母顺序第二靠前的那本书。此时，你的书架看起来像这样：

• 《Anna Karenina》
• 《Moby Dick》
• 《War and Peace》
• 《Don Quixote》
• 《Crime and Punishment》

你会再次从左到右依次查看剩下的书籍的书名，发现《Crime and Punishment》是字母顺序第二靠前的那本书。然后，你将这本书从原来的位置上取下来，放到书架的第二个位置上。你继续重复上述步骤，直到所有书籍都被整理好。最终，你的书架上的书籍将按照书名字母顺序排列好。这个整理书架的过程实际上就是选择排序的一个实际应用。在每一步中，你都在未排序的书籍中找到最小（或最大）的书籍，并将其放到已排序部分的末尾。这与我们要讲的选择排序的工作原理非常相似。

选择排序的基本思想就是：通过n-1次关键字间的比较，从n-i+1个记录中选取到关键字最小的记录，并和第i（1≤ i  ≤n）个记录进行交换。

选择排序

1.2选择排序的实现

我们知道了选择排序是将选取到的最小值放到第i个位置，那这个思想能不能的搭配优化呢？当然是有的，我们在遍历时会选取最小值，那我们就顺手选取出最大值，将其放在待排序列的末尾，并同时缩小待排序序列的长度区间，我们先看实现再进行逐步分析：

void Selectsort(int* arr, int n)
{
int begin = 0;
int end = n – 1;
//一直在[begin,end]区间进行排序，
//标记最大值和最小值将其移动到begin/end处，再缩小[begin,end]区间
while (end >begin)
{
//先假设最大和最小值都是begin
int maxi = begin;
int mini = begin;
//从begin下一个元素开始遍历到end找出其中最大最小值
for (int i = begin+1; i <= end; i++)
{
if (arr[i] > arr[maxi])
{
maxi = i;
}
if (arr[i] < arr[mini])
{
mini = i;
}
}
if (maxi == begin)
{
maxi = mini;
}
swap(&arr[mini], &arr[begin]);
swap(&arr[maxi], &arr[end]);
begin++;
end–;
}
}

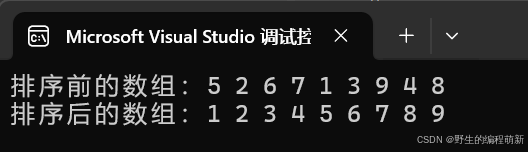
传统的选择排序在每一轮中只找一个最大或最小元素，而这种优化版本在一次遍历中同时找出最大值和最小值，并将它们放置在正确位置，从而将排序所需的迭代次数减少了一半。

1.3时间复杂度的分析

又到时间复杂度分析了，我们先让他跑一下10000个数据花费多久，然后再进行讨论：

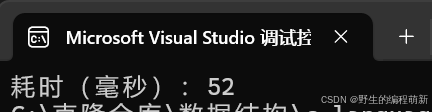
从这个运行时间我们就知道这个排序算法的时间复杂度不会低，我们开始计算这个算法的时间复杂度吧：

1.外层循环：假设待排序的序列长度为n，将会执行n/2次，每次迭代都会减少区间（begin++和                           end–），区间大小减少2.

2.内层循环：在每次外层循环迭代中，内层循环将遍历未排序部分的所有元素，以找到最大和最小                       元素的索引。因此，内层循环的执行次数将逐渐减少，第一次执行n-1次，第二次执                       行n-3次，以此类推。

所以选择排序的时间复杂度为：（n-2）*[(n-1)+(n-3)+(n-5)+…..+1]，化简后为O(n²)。即使待排序序列已经有序，仍需执行完所有的比较，所以选择排序的时间复杂度为O(n²)。

2.快速排序

2.1引入

终于到我们的王牌登场了，如果你将来工作时，你的老板让你写一个排序算法，而你会的算法中竟然没有快速排序，我建议你去偷偷的复制一份快速排序到你的电脑中，这样你至少不会被大家取笑。

快速排序是有英国计算机科学家托尼.霍尔(Tony Hoare)于1960年提出的，是计算机科学史上首个实现​​分治策略​​的高效排序算法。其核心思想通过基准值划分数组，将复杂问题分解为可递归解决的子问题，它以其高效性和广泛的应用在排序算法中占据了重要地位，奠定了现代算法设计的范式。

Tony Hoare是20世纪最伟大的计算机科学界之一，而这快速排序算法只是他众多贡献中的一个小发明而已（有时候真想这些这么牛的人拼了…）。更牛的是我们现在要讲的快速排序算法被列为20世纪十大算法之一，我们这些玩编程的还有什么理由不去学它呢？

快速排序其实就是前面我们认为最慢的冒泡排序的升级。他们都是属于交换类排序，他也是通过不断的比较和移动交换来实现排序的，只不过他的实现，增大了记录的比较和移动距离，将关键字较大的记录从前面直接移动到后面，关键字较小的记录直接从后面移动到前面，从而减少了总的比较次数和移动次数。

2.2快速排序的实现

快速排序的基本思想：通过一趟排序将待排序列分成独立的两部分，其中一部分的所有元素均比另一部分的所有元素要小，然后再按此方法对这两部分继续进行排序，以达到整个序列有序。我们先来看一下下面这段小视频来感受一下：

快排

知道了它的排序操作了，我们来实现一下：

2.2.1Hoare版本实现

快排有好多种实现版本，我们先来实现祖师爷的版本：

int _Quicksort(int* a,int left,int right)
{
int keyi = left;
left++;//从基准值的后一个元素开始遍历
//保证在正确的区间进行
while (left <= right)
{
while (left <= right && a[right] > a[keyi])
{
right–;
}
while (left <= right && a[left] < a[keyi])
{
left++;
}

if (left <= right)
{
swap(&a[left++], &a[right–]);
}
}
swap(&a[keyi], &a[right]);
return right;
}
void Quicksort(int* a, int left,int right)
{
//不在区间范围直接返回
if (left>=right)
{
return;
}
int keyi = _Quicksort(a, left, right);
Quicksort(a, left, keyi – 1);
Quicksort(a, keyi + 1, right);
}

在这里我们实现了两个函数，这两个函数的功能分别为：

1._Quicksort：执行单次分区操作的函数

2.Quicksort：快速排序的主控函数，负责递归调用

_Quicksort函数：

Quicksort函数：

2.2.2lomuto版本实现

lomuto版本的思想就是使用前后指针来实现：

int _QuickSort(int* a, int left, int right)
{
int keyi = left;
int prev = left, cur = prev + 1;
while (cur <= right)
{
if (a[cur] < a[keyi] && ++prev != cur)
{
Swap(&a[prev], &a[cur]);
}
cur++;
}
Swap(&a[keyi], &a[prev]);
return prev;
}

在这里只需要替换掉Hoare版本中的_Quicksort函数就行了，Lomuto版本是快速排序最直观易懂的实现方式之一，那么现在我们来详细讲讲其工作原理：

2.3快速排序的时间复杂度分析

老样子还是要走一下的，先跑一万个数据看一下：

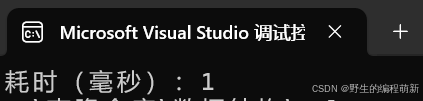
是不是非常离谱，王牌排序！现在我们进入正题：

快速排序是递归算法，总时间复杂度 = 单次分区时间 × 递归调用次数。

最好情况：

每次分区都能将数组均匀划分为左右两部分​，例如：子数组长度为 n，划分后左右子数组长度均为 n/2。

​深度：递归树的深度为 ​​log₂n​

每层总操作数：每层所有节点的分区操作总和为 n（因为每层划分的总元素数不变，仅子问                             题规模减半）。

总时间复杂度：T(n)=O(n)+O(n)+…+O(n)（一共 ​​log₂n​层）=O(n* ​​log₂n​)

最坏情况：

每次分区都极度不平衡，导致一侧子数组长度为 ​​0​​，另一侧为 ​​n-1​​。例如：输入数组 ​​已排序​​ 或 ​​逆序​​，且每次选择第一个元素作为基准值。

深度：递归树退化为链表，深度为 ​​n​​（每次仅减少1个元素）。

每层总操作数：第1层：操作量 n，第2层：操作量 n-1，第3层：操作量 n-2…..第n层：操                           作量 1

总时间复杂度：T(n)=O(n)+O(n-1)+….+O(1)=O(n(n+1)/2)=O(n²)