2025级大一ACM训练：二进制枚举

前言

对于一个包含n个元素的集合，每个元素有 “选” 和 “不选” 两种状态，总共有2^n种子集（包括空集）。用一个n位的二进制数来表示一种选取状态：

        二进制位为1：表示对应位置的元素被选中；

        二进制位为0：表示对应位置的元素未被选中。

异或运算：

        X ^ X = 0        X ^ 0 = X

林大OJ 643：teacher Li

注意：数组a,b定义成全局变量，这样存在静态区，会自动初始化为0，有助于我们的异或运算

#include <bits/stdc++.h>
using namespace std;

int n,cnt;
char a[35], b[35];

int main()
{
while(~scanf("%d",&n))
{
cnt++;
scanf("%s",a);
for(int i = 1; i <= 2 * n – 2; i++)
{
scanf("%s", b);
int len = strlen(b);
for(int j = 0; j < len; j++)
{
a[j] = a[j] ^ b[j];
}
}
printf("Scenario #%d\\n",cnt);
printf("%s\\n\\n",a);
}
return 0;
}

林大OJ 1172：Find different

#include <bits/stdc++.h>
using namespace std;

int n,x;
int main()
{
while(~scanf("%d",&n))
{
int ans = 0;
while(n–)
{
scanf("%d",&x);
ans = ans ^ x;
}
printf("%d\\n",ans);
}
return 0;
}

林大OJ 1205：和为K–二进制枚举

两个二进制数进行与运算，只有对应位置都是1才是1，有一个位置是0就是0，例如：010&110 = 1，010&101 = 0

枚举所有子集：i < (1<<N)

1<<N 等价于 2^N，表示长度为 N 的数组共有 2^N 个子集（包括空集）。

判断是否选中元素：i & (1<<j)

1<<j：生成一个 “只有第 j 位是 1，其余位都是 0” 的数（比如 j=0→1=001，j=1→2=010，j=2→4=100）；

i & (1<<j)：按位与运算，只有当 i 的第 j 位是 1 时，结果才 ≠ 0（表示选中），否则 = 0（不选）。

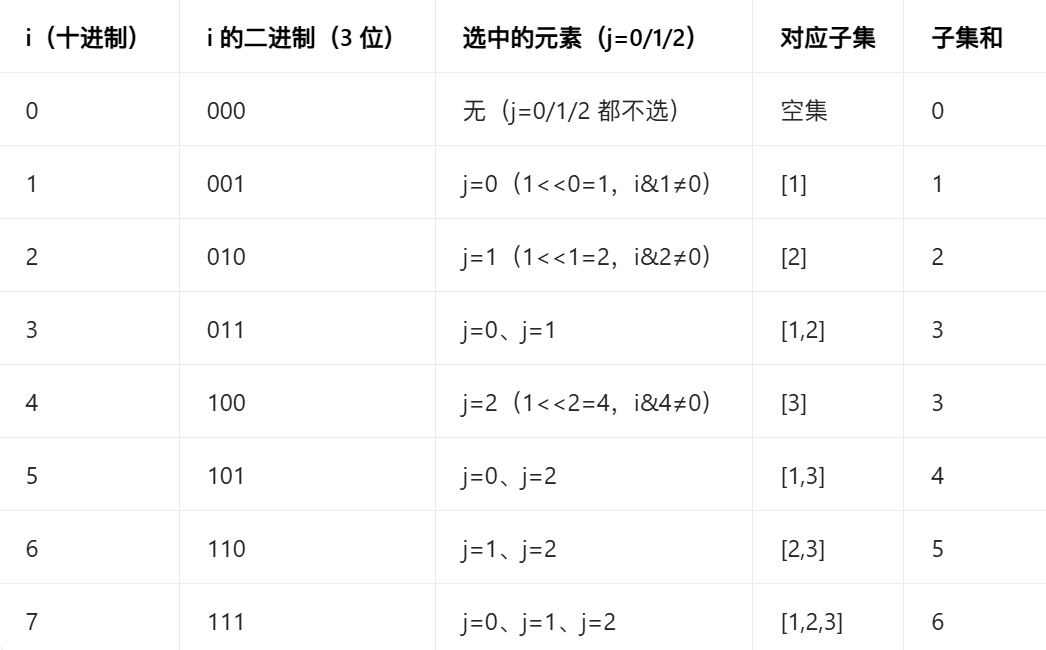
这块比较难理解，我们以n=3，k=5举例，假设那三个数是[1，2，3]，我们看下面这张表，这时     i < (1<<3)即 i<8, 共有八个子集。

#include <bits/stdc++.h>
using namespace std;

int a[25];

int main()
{
ios::sync_with_stdio(false);
int N, K;
while(cin>>N>>K)
{
for(int i = 0; i < N; i++)
cin>>a[i];

int f = 1;

for(int i = 0; i <(1<<N); i++)//遍历每一种子集的情况
{
int sum = 0;
for(int j = 0; j < N; j++)
{
if(i & (1<<j))//表示当1的第j位是1时，才选中
{
sum += a[j];
}
}
if(sum ==K)
{
cout<<"Yes"<<endl;
f = 0;
break;
}
}
if(f == 1)
cout<<"No"<<endl;
}
return 0;
}

林大OJ 1505：陈老师加油-二进制枚举

说明：第一层循环循环相当于枚举出所有的情况，第二层循环是看这个01串上的各位是0还是1，如果是0的话就当作加油站计数，如果为1就把当作路口计数，计数结束以后或者油不够了的话就退出判断，如果加油站数量和路口数量满足要求了而且油恰好用完的话，这此枚举到的这种情况就是符合要求的把计算进来。

把和为k那道题理解明白之后在做这个就会好很多哦

#include <bits/stdc++.h>
using namespace std;

int main()
{
ios::sync_with_stdio(false);
int T;
while(cin>>T)
{
int cnt = 0;
for(int i = 0; i<(1<<15); i++)//相当于一个15位的01串，如果是0，表示遇到加油站，是1表示遇到十字路口
{
int cross_road=0, gap_station=0, tmp = T;
for(int j = 0; j<15; j++)
{
if(i & (1<<j) && tmp >0)
{
tmp -=1;
cross_road++;
}
else if(tmp > 0)
{
tmp *= 2;
gap_station++;
}
}
if(gap_station==5 && cross_road == 10 &&tmp == 0)
cnt++;
}
cout<<cnt<<endl;
}
return 0;
}

林大OJ 1518：纸牌游戏-二进制-搜索

这道题和和为K–二进制枚举很相似！

#include <bits/stdc++.h>
using namespace std;

int main()
{
ios::sync_with_stdio(false);
int n, p;
int a[25];
while(cin>>n>>p)
{
int cnt = 0;
for(int i = 0; i <n; i++)
cin>>a[i];
for(int i = 1; i < (1<<n); i++)//不需要统计空集
{
int ans=0;
for(int j = 0; j < n; j++)
{
if(i & (1<<j))
{
ans+=a[j];
}
}
if(ans == p)
cnt++;
}
cout<<cnt<<endl;
}
return 0;
}

林大OJ 1641：权利指数

核心逻辑：二进制枚举所有子集 → 筛选获胜联盟 → 遍历联盟找关键加入者 → 统计权利指数；

关键技巧：用位运算判断成员是否在联盟中，用 “移除后票数和” 判断是否为关键加入者；

#include <bits/stdc++.h>
using namespace std;

int main()
{
ios::sync_with_stdio(false);
int T;
cin>>T;
while(T–)
{
int n;
cin>>n;
vector<int> votes(n); //存储每个小团体的票数
int total = 0;
for(int i = 0; i < n; i++)
{
cin>>votes[i];
total += votes[i];
}

double half_votes = total / 2.0;
vector<int> power(n, 0);

//空集一定不是获胜联盟
for(int i = 1; i < (1<<n); i++){
int sum = 0;
for(int j = 0; j < n; j++)
{
if(i & (1<<j)){sum +=votes[j];}
}

//判断是否为获胜联盟
if(sum <= half_votes)
continue;

for(int j = 0; j < n; j++){
if(i & (1<<j))
{
int sum_without_j = sum – votes[j];
if(sum_without_j <= half_votes)
power[j]++;
}
}
}
for(int i = 0; i < n; i++){
cout<<power[i];
if(i != n-1)
cout<<" ";
}
cout<<endl;
}
return 0;
}

林大OJ 1285：趣味解题

组合概率 = 做对题的 AC 概率乘积 × 做错题的 WA 概率乘积

一个组合是 “多个独立事件（每题的对 / 错）同时发生”，因此概率是各事件概率的乘积所有 “做对题数 = cnt=x” 的组合概率相加，就是最终答案。

#include <bits/stdc++.h>
using namespace std;

int main() {
ios::sync_with_stdio(false);
int T;
cin >> T;
while (T–) {
int n, x;
double a[15], b[15], c[15];
double ac[15], wa[15];
cin >> n;

for (int i = 0; i < n; i++) cin >> a[i];
for (int i = 0; i < n; i++) cin >> b[i];
for (int i = 0; i < n; i++) cin >> c[i];
cin >> x;

for (int i = 0; i < n; i++) {
wa[i] = (1 – a[i]) * (1 – b[i]) * (1 – c[i]); // 三人都做错的概率
ac[i] = 1 – wa[i];
}

double ans = 0.0; // 初始化结果为0（关键！）
// 枚举所有做题状态（i的二进制位表示每道题是否AC）
for (int i = 0; i < (1 << n); i++) {
int cnt = 0;
double p = 1.0;
for (int j = 0; j < n; j++) {
if (i & (1 << j)) { // 第j题做对
p *= ac[j];
cnt++;
} else { // 第j题做错
p *= wa[j];
}
}
//把每种组合的概率加在一起
if (cnt == x) {
ans += p;
}
}

printf("%.4lf\\n", ans);
}
return 0;
}