力扣解题-盛最多水的容器

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

示例 1：
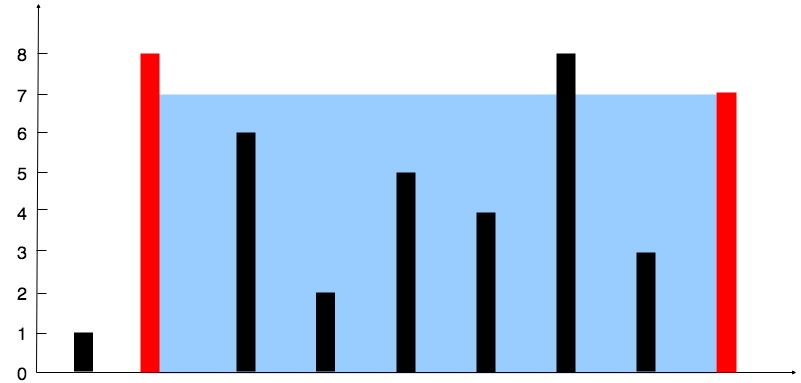
在这里插入图片描述

输入：[1,8,6,2,5,4,8,3,7]
输出：49
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：
输入：height = [1,1]
输出：1

提示：
n == height.length
2 <= n <= 105
0 <= height[i] <= 104

第一次解答（失败，超时）

解题思路

核心方法：暴力枚举所有垂线组合，遍历数组中每一对不同的垂线，计算每对垂线构成容器的盛水量，最终取所有结果的最大值，逻辑简单但时间效率极低。

具体步骤：

初始化最大盛水量max为0，用于记录遍历过程中找到的最大水量。

外层循环遍历数组的每个下标i（代表第一条垂线的位置），内层循环遍历i之后的所有下标j（代表第二条垂线的位置，j > i避免重复计算同一对垂线）。

对于每对(i, j)，计算容器的盛水量：盛水量 = 两条垂线的水平距离 × 两条垂线中较矮的高度，即(j – i) * Math.min(height[i], height[j])。

用当前计算的盛水量更新max（取max和当前值的较大者）。

两层循环结束后，返回max作为最大盛水量。

失败原因分析

该解法超时的核心原因是时间复杂度过高，无法适配题目数据规模：

时间复杂度为O(n²)：外层循环执行n次，内层循环平均执行n/2次，总计算次数约为n²/2。对于题目中n <= 10^5的限制，总计算次数会达到5×10^9级别，远超程序运行的时间阈值（通常OJ单题允许的计算次数约10^8），必然触发超时。

无任何优化策略：暴力枚举了所有可能的组合，未利用“盛水量由矮边决定”的核心特性进行剪枝，存在大量无意义的计算，完全无法满足大数据量的性能要求。

public int maxArea(int[] height) {
int max=0;
for(int i=0;i<height.length;i++){
for(int j=i+1;j<height.length;j++) {
max = Math.max(max, (j – i) * Math.min(height[i], height[j]));
}
}
return max;
}

第二次解答

解题思路

核心方法：双指针贪心策略 + 向中间收缩逼近最大值，利用“盛水量由矮边决定”的特性，从数组两端向中间移动指针，仅需一次遍历即可找到最大盛水量，时间复杂度优化至O(n)。

具体步骤：

初始化双指针：左指针left指向数组起始位置（下标0），右指针right指向数组末尾位置（下标height.length-1）；同时初始化最大盛水量max为0。

开启循环（终止条件：left >= right，即两指针相遇时停止）：
a. 计算当前双指针构成容器的盛水量：Math.min(height[left], height[right]) * (right – left)，并用该值更新max。
b. 贪心收缩指针：比较height[left]和height[right]的大小，移动较矮的那个指针：
– 若height[left] < height[right]：左指针left右移一位（left++）；
– 否则：右指针right左移一位（right–）。

循环结束后，max即为能容纳的最大水量，返回该值。

核心优化逻辑说明

移动较矮指针的合理性（贪心策略的核心）：

容器的盛水量由两指针的水平距离和两指针中较矮的高度共同决定，即水量 = 距离 × 矮边高度。
若移动较高的指针：水平距离会减小，而矮边高度不会增加（甚至可能不变/减小），盛水量必然不会增大；
若移动较矮的指针：水平距离减小，但有可能找到更高的边，从而让矮边高度提升，弥补距离减小的损失，最终可能得到更大的盛水量。
该策略确保每一步移动都朝着“可能增大盛水量”的方向，且仅需一次遍历，时间复杂度从O(n²)降至O(n)，完全适配10^5级别的数据规模。

执行耗时:5 ms,击败了32.91% 的Java用户
内存消耗:76 MB,击败了19.06% 的Java用户

public int maxArea(int[] height) {
int left =0;
int right = height.length–1;
int max = 0;
while (left<right){
max= Math.max(max,Math.min(height[left],height[right])*(right–left));
if(height[left]<height[right]){
left++;
}else{
right—;
}
}
return max;
}

总结

第一次解答的暴力枚举法因O(n²)的时间复杂度，在n=10^5时计算量超限，直接超时；其仅适用于极小数据量，无法满足题目要求。

第二次解答的双指针贪心策略是本题的最优解：利用“盛水量由矮边决定”的特性，通过移动较矮指针收缩范围，仅需O(n)时间复杂度完成遍历，高效找到最大盛水量。

本题的核心解题思路是放弃无意义的全量枚举，通过贪心策略缩小搜索范围，用“空间换时间”的反向思路（双指针仅占用常数空间），以最优的时间效率解决问题。

力扣解题-盛最多水的容器