day24 代码随想录算法训练营 回溯专题3

1 今日打卡

复原IP地址 93. 复原 IP 地址 – 力扣（LeetCode）

子集 78. 子集 – 力扣（LeetCode）

子集Ⅱ 90. 子集 II – 力扣（LeetCode）

2 复原IP地址

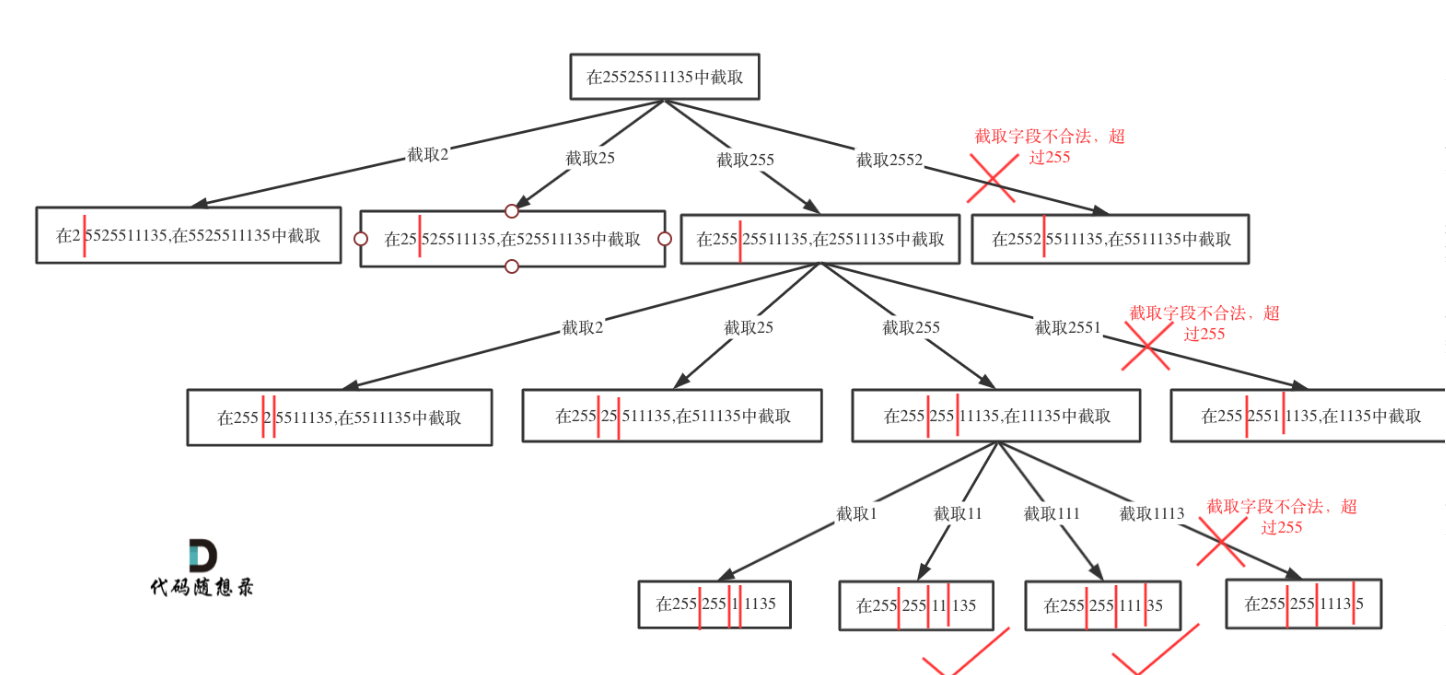
2.1 思路

startIndex：字符串当前分割的起始索引（避免重复分割字符） pointNum：已添加的点的数量（点的数量为 3 时，说明已分成 4 段，触发终止条件） 终止条件：点的数量pointNum == 3，此时只需验证最后一段是否合法，合法则拼接成 IP 地址加入结果集 单层递归逻辑：从startIndex开始，遍历字符串尝试分割出1~3 位的子串（IP 段最多 3 位），验证子串合法后，将其加入临时路径，递归处理下一段，递归结束后回溯重置状态（移除临时路径的最后一段、点的数量减 1） 合法性校验：单独封装isValid方法，判断分割出的子串是否为有效 IP 段

用 List<String>存储路径，而不是 StringBuilder，否则会很复杂。

在合法性校验中，需要加start > end返回flase的判断，否则会出现空指针异常。因为如果前面三段把字符串分割完了，再进入下一层递归的时候，start的值会比end还大，这个时候s.charAt(start)就会有空指针异常。

2.2 实现代码

class Solution {
// 结果集：存储所有合法的IP地址
List<String> res = new ArrayList<>();
// 路径集：存储回溯过程中分割出的合法IP段（最多3段，因为pointNum=3时处理最后一段）
List<String> path = new ArrayList<>();

/**
* 主方法：入口，初始化并调用回溯方法
* @param s 输入的数字字符串
* @return 所有合法的IP地址列表
*/
public List<String> restoreIpAddresses(String s) {
// 前置剪枝：IP地址总长度最小4位（0.0.0.0），最大12位（255.255.255.255），不符合直接返回空
if (s.length() < 4 || s.length() > 12) return res;
// 调用回溯方法，初始：分割起始索引0，已添加点数量0
backtracking(s, 0, 0);
return res;
}

/**
* 回溯核心方法
* @param s 输入的数字字符串
* @param startIndex 当前分割的起始索引（避免重复分割）
* @param pointNum 已添加的点的数量（点数量=3时，分成4段，触发终止）
*/
public void backtracking(String s, int startIndex, int pointNum) {
// 终止条件：已添加3个点，说明字符串已被分成前3段，只需处理最后一段
if(pointNum == 3) {
// 验证最后一段是否合法：起始索引startIndex 到 字符串末尾
if(isValid(s, startIndex, s.length() – 1)) {
// 拼接合法IP：路径集的3段 + 最后一段，用点分隔
String ip = path.get(0) + "." + path.get(1) + "." + path.get(2) + "." + s.substring(startIndex, s.length());
res.add(ip); // 加入结果集
}
return; // 终止递归，返回上一层
}

// 单层递归：遍历字符串，尝试分割1~3位的子串（i < startIndex + 3 限制最多3位）
for(int i = startIndex; i < s.length() && i < startIndex + 3; i++) {
// 验证当前分割的子串[startIndex, i]是否为有效IP段
if(isValid(s, startIndex, i)) {
// 合法则加入路径集：截取[startIndex, i]的子串
path.add(s.substring(startIndex, i + 1));
pointNum++; // 点的数量+1
// 递归处理下一段：下一段起始索引为i+1，点数量+1
backtracking(s, i + 1, pointNum);
// 回溯：重置状态，恢复到递归前的样子（核心！）
pointNum–; // 点的数量减1
path.remove(path.size() – 1); // 移除路径集最后一个添加的IP段
}
}
}

/**
* 校验方法：判断字符串s中[start, end]区间的子串是否为有效IP段
* @param s 输入的数字字符串
* @param start 子串起始索引
* @param end 子串结束索引
* @return 有效返回true，无效返回false
*/
public boolean isValid(String s, int start, int end) {
// 边界判断：起始索引大于结束索引，空段，直接无效
if(start > end) return false;
// 长度判断：IP段最多3位，超过则无效（循环已限制，此处做双重校验）
if(end – start >= 3) return false;
// 前导0判断：以0开头且长度大于1，无效（如01、012，单独0合法）
if(s.charAt(start) == '0' && start != end) {
return false;
}
// 数字判断：遍历子串，确保每一位都是数字（避免非数字字符，题目虽给数字串，此处做防御性校验）
int index = start;
while(index <= end) {
// 非0-9的字符，无效
if(s.charAt(index) > '9' || s.charAt(index) < '0') {
return false;
}
index++;
}
// 数值判断：截取子串转整数，判断是否<=255
String substr = s.substring(start, end + 1);
if(Integer.parseInt(substr) > 255) {
return false;
}
// 所有校验通过，是有效IP段
return true;
}
}

3 子集

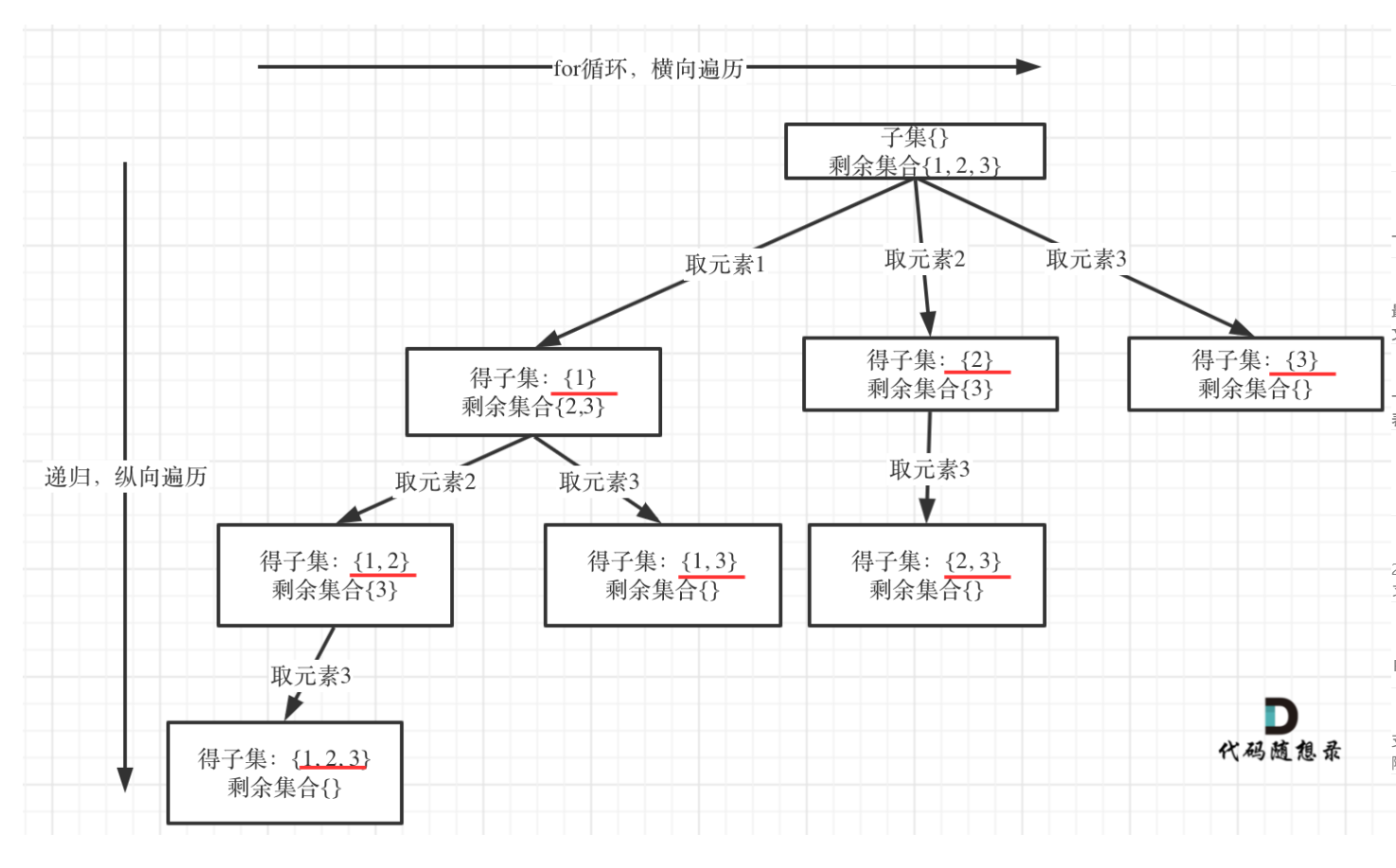
3.1 思路

子集的本质是从数组中选择任意数量的元素（包括 0 个），不考虑顺序且不重复选择，回溯法通过控制起始索引避免重复选择，通过进入递归时立即收集结果实现「所有节点都加入解集」，整体思路是构建一棵子集树，遍历树的所有节点并收集。 回溯法核心要素（子集问题专属） 1. 状态变量 仅需 **startIndex：当前选择元素的起始索引，用于控制元素选择的范围 **，避免重复选择（如选了 1 之后只能选 1 后面的元素，防止出现 [1,2] 和 [2,1] 这种重复子集）。 2. 结果收集时机（最核心的区别） 进入递归方法后，立即将当前路径加入结果集—— 因为子集树的每一个节点（包括空节点、中间节点、叶子节点）都是一个合法子集，这是子集问题与其他回溯问题的关键差异。 3. 终止条件（可省略，做防御性判断） 当startIndex >= nums.length时，说明数组已遍历完毕，无元素可再选择，直接返回即可。 4. 单层递归逻辑 从startIndex开始遍历数组，将当前元素加入路径→递归选择下一个元素（起始索引i+1）→递归结束后回溯重置状态（移除路径最后一个元素），尝试下一个元素的选择。

3.2 实现代码

class Solution {
// 结果集：存储所有合法的子集，每个子集是一个List<Integer>
List<List<Integer>> res = new ArrayList<>();
// 路径集：存储回溯过程中当前选择的元素组合（即当前子集）
List<Integer> path = new ArrayList<>();

/**
* 主方法：入口，初始化并调用回溯方法求解子集
* @param nums 输入的无重复整数数组
* @return 数组的所有子集
*/
public List<List<Integer>> subsets(int[] nums) {
// 调用回溯方法，初始起始索引为0（从数组第一个元素开始选择）
backtracking(nums, 0);
return res;
}

/**
* 回溯核心方法：构建子集树，收集所有节点的路径（子集）
* @param nums 输入的无重复整数数组
* @param startIndex 当前选择元素的起始索引（控制选择范围，避免重复）
*/
public void backtracking(int[] nums, int startIndex) {
// 核心步骤：进入递归立即收集当前路径 → 子集树的每个节点都是合法子集
// 注意：必须new ArrayList<>(path)，否则所有res元素都指向同一个path对象，最终结果会被覆盖
res.add(new ArrayList<>(path));

// 终止条件：起始索引超出数组长度，无元素可再选择，直接返回
// 注：此终止条件可省略，因为for循环会因i < nums.length自动终止，此处做防御性判断更健壮
if (startIndex >= nums.length) {
return;
}

// 单层递归逻辑：从startIndex开始遍历，选择当前元素并递归
for (int i = startIndex; i < nums.length; i++) {
path.add(nums[i]); // 选择当前元素nums[i]，加入路径集
backtracking(nums, i + 1); // 递归：选择下一个元素，起始索引为i+1（避免重复选择）
path.remove(path.size() – 1); // 回溯：移除路径集最后一个元素，恢复到递归前的状态
}
}
}

4 子集Ⅱ

4.1 思路

数组排序：先对nums进行升序排序，让相同元素相邻—— 这是去重的前提，只有相同元素挨在一起，才能方便地判断并跳过重复元素； 回溯构建子集：沿用普通子集的回溯逻辑（进入递归立即收集结果、控制startIndex避免重复选择）； 同层去重：在单层递归的循环中，判断当前元素是否与前一个元素相同，且前一个元素未被选择（同层），若是则跳过该元素，避免同层选择重复元素导致子集重复。

状态变量：仅需startIndex（当前选择元素的起始索引，控制选择范围，避免跨层重复选择）； 结果收集时机：进入递归立即收集当前路径（子集树的每个节点都是合法子集，与普通子集一致）； 终止条件：startIndex >= nums.length，无元素可选择时直接返回（防御性判断，可省略）； 单层递归逻辑：从startIndex遍历数组→跳过同层重复元素→选择当前元素→递归→回溯重置状态； 去重关键：if (i > startIndex && nums[i] == nums[i-1]) continue;—— 这行代码是本题的灵魂，专门拦截同层重复元素。

4.2 实现代码

class Solution {
// 结果集：存储所有不重复的子集，每个子集是一个List<Integer>
List<List<Integer>> res = new ArrayList<>();
// 路径集：存储回溯过程中当前选择的元素组合（当前子集）
List<Integer> path = new ArrayList<>();

/**
* 主方法：入口，排序数组+调用回溯方法求解不重复子集
* @param nums 输入的可能包含重复元素的整数数组
* @return 数组的所有不重复子集
*/
public List<List<Integer>> subsetsWithDup(int[] nums) {
// 核心步骤1：数组排序，让相同元素相邻 → 为后续同层去重做准备（去重的前提）
Arrays.sort(nums);
// 调用回溯方法，初始起始索引为0（从数组第一个元素开始选择）
backtracking(nums, 0);
return res;
}

/**
* 回溯核心方法：构建子集树，收集所有节点的路径，同时跳过同层重复元素去重
* @param nums 排序后的整数数组（相同元素相邻）
* @param startIndex 当前选择元素的起始索引（控制选择范围，避免跨层重复）
*/
public void backtracking(int[] nums, int startIndex) {
// 核心步骤：进入递归立即收集当前路径 → 子集树的每个节点都是合法子集
// 必须new ArrayList<>(path)：保存当前路径快照，避免引用覆盖（普通子集的核心坑）
res.add(new ArrayList<>(path));

// 终止条件：起始索引超出数组长度，无元素可再选择，直接返回
// 注：可省略，for循环会因i < nums.length自动终止，此处做防御性判断更健壮
if (startIndex >= nums.length) {
return;
}

// 单层递归逻辑：从startIndex开始遍历，选择元素并递归，同时跳过同层重复元素
for (int i = startIndex; i < nums.length; i++) {
// 核心步骤2：同层去重 → 跳过当前层的重复元素，避免生成重复子集
// 条件解读：
// 1. i > startIndex：表示当前元素不是当前层的第一个元素（同层后续元素）
// 2. nums[i] == nums[i-1]：表示当前元素与前一个元素相同
// 满足则跳过，不选择当前元素
if (i > startIndex && nums[i] == nums[i – 1]) {
continue;
}
path.add(nums[i]); // 选择当前元素nums[i]，加入路径集
backtracking(nums, i + 1); // 递归：选择下一个元素，起始索引为i+1（避免跨层重复）
path.remove(path.size() – 1); // 回溯：移除路径集最后一个元素，恢复递归前的状态
}
}
}