94. 二叉树的中序遍历

94. 二叉树的中序遍历

简单

给定一个二叉树的根节点 root ，返回 它的 中序 遍历 。

示例 1：

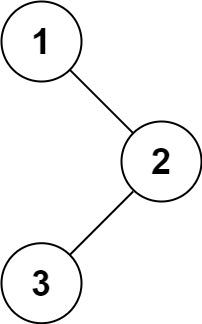
输入：root = [1,null,2,3]
输出：[1,3,2]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

提示：

• 树中节点数目在范围 [0, 100] 内
• -100 <= Node.val <= 100

进阶: 递归算法很简单，你可以通过迭代算法完成吗？

这是为您定制的 二叉树的中序遍历 (递归法 / DFS) 复习笔记。

欢迎正式进入 二叉树 (Binary Tree) 的世界！ 这份代码是二叉树遍历的 “母题”。虽然递归写法只有寥寥几行，但它是理解 DFS (深度优先搜索) 的基石。您注释里提到的“代码移到前面/后面就是前/后序”，一语道破了 DFS 的天机。

📝 核心笔记：二叉树的中序遍历 (Inorder Traversal)

1. 核心思想 (一句话总结)

“左 -> 中 -> 右：先一路走到最左下角，打印出来，退回一步打印中间，再去右边转转。”

• 前序 (Pre-order)：根 -> 左 -> 右 (先办事，再跑腿)
• 中序 (In-order)：左 -> 根 -> 右 (先跑到底，回来办事，再继续跑)
• 后序 (Post-order)：左 -> 右 -> 根 (最后办事)

2. 核心特性 (BST 的秘密)

中序遍历有一个 价值连城的特性，请务必刻在脑海里：

如果是 二叉搜索树 (BST)，中序遍历的结果是一个 升序数组。 很多验证 BST、找 BST 第 K 小元素的题目，本质上就是考中序遍历。

3. 算法流程 (递归视角)

🔍 代码回忆清单

// 题目：LC 94. Binary Tree Inorder Traversal
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> ans = new ArrayList<>();
dfs(ans, root);
return ans;
}

private void dfs(List<Integer> ans, TreeNode node) {
// 1. Base Case: 撞墙回头
if (node == null) {
return;
}

// 2. 递归去左边 (L)
dfs(ans, node.left);

// 3. 处理中间 (Root) – 中序的位置
ans.add(node.val);

// 4. 递归去右边 (R)
dfs(ans, node.right);
}
}

⚠️ 面试高频扩展 (Iterative / 迭代法)

面试官经常会问：“如果递归栈溢出怎么办？能不能用迭代（栈）来实现？” 这是为了考察你对 “系统调用栈” 的模拟能力。

核心逻辑：

// 迭代法模版 (一定要背下来)
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
Deque<TreeNode> stack = new ArrayDeque<>();

// 指针 cur 从 root 开始
TreeNode cur = root;

// 只要 cur 还有路走，或者栈里还有存货，就继续
while (cur != null || !stack.isEmpty()) {
// 1. 既然非空，就一路向左，把沿途的都压进去
if (cur != null) {
stack.push(cur);
cur = cur.left;
}
// 2. 走到头了 (cur == null)，开始弹栈
else {
cur = stack.pop(); // 弹出栈顶元素
res.add(cur.val); // 【中序】在这里记录值
cur = cur.right; // 转向右子树
}
}
return res;
}

🖼️ 数字演练

树结构：

1
/ \\
2 3

递归视角：

结果：[2, 1, 3]