洛谷 P11230：[CSP-J 2024 T4] 接龙 ← 图论+动态规划

【题目来源】 https://www.luogu.com.cn/problem/P11230 https://www.acwing.com/problem/content/6044/ 【题目描述】 在玩惯了成语接龙之后，小 J 和他的朋友们发明了一个新的接龙规则。 总共有 n 个人参与这个接龙游戏，第 i 个人会获得一个整数序列 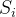作为他的词库。 一次游戏分为若干轮，每一轮规则如下： （1）n 个人中的某个人 p 带着他的词库 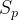进行接龙。若这不是游戏的第一轮，那么这一轮进行接龙的人不能与上一轮相同，但可以与上上轮或更往前的轮相同。 （2）接龙的人选择一个长度在 [2,k] 的 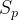的连续子序列 A 作为这一轮的接龙序列，其中 k 是给定的常数。若这是游戏的第一轮，那么 A 需要以元素 1 开头，否则 A 需要以上一轮的接龙序列的最后一个元素开头。– 序列 A 是序列 S 的连续子序列当且仅当可以通过删除 S 的开头和结尾的若干元素（可以不删除）得到 A。 为了强调合作，小 J 给了 n 个参与游戏的人 q 个任务，第 j 个任务需要这 n 个人进行一次游戏，在这次游戏里进行恰好 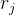轮接龙，且最后一轮的接龙序列的最后一个元素恰好为 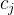。 为了保证任务的可行性，小 J 请来你判断这 q 个任务是否可以完成的，即是否存在一个可能的游戏过程满足任务条件。 【输入格式】 本题有多组测试数据。 输入的第一行包含一个正整数 T，表示数据组数。 接下来包含 T 组数据，每组数据的格式如下： 第一行包含三个整数 n,k,q，分别表示参与游戏的人数、接龙序列长度上限以及任务个数。 接下来 n 行： 第 i 行包含 (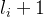) 个整数 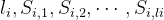，其中第一个整数 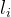表示序列 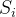的长度，接下来 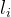个整数描述序列 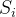。 接下来 q 行： 第 j 行包含两个整数 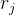,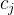，描述一个任务。 【输出格式】 对于每个任务：输出一行包含一个整数，若任务可以完成输出 1，否则输出 0。 【输入样例】 1 3 3 7 5 1 2 3 4 1 3 1 2 5 3 5 1 6 1 2 1 4 2 4 3 4 6 6 1 1 7 7 【输出样例】 1 0 1 0 1 0 0 【数据范围】 对于所有测试数据，保证： 1≤T≤5； 1≤n≤10^5，2≤k≤2×10^5，1≤q≤10^5； 1≤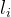≤2×10^5，1≤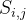≤2×10^5； 1≤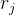≤10^2，1≤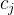≤2×10^5； 设 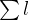为单组测试数据内所有 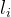的和，则 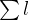≤2×10^5。 【算法分析】 本题是一个典型的图论可达性问题，结合动态规划思想解决特定条件下的路径查询。 如下代码实现了一个基于状态转移的路径查询系统，主要功能是判断特定条件下节点间的可达性。以下是核心解析： 一、数据结构与初始化 ‌1.全局变量定义‌ v[N]：存储每个节点的邻接表，v[i] 表示节点 i 的连接序列‌。 st[M][N]：状态矩阵，st[i][j] 记录在第 i 步能否到达节点 j，初始值为 -1‌。 常量 N=2e5+5 和 M=1e2+5 分别限制节点数和最大步数。 ‌2.输入处理‌ 读取测试用例数 T 后，循环处理每组数据‌。 对每个节点 i，先清空邻接表，再读入其连接序列（如输入 5 1 2 3 4 1 表示节点 i 有 5 个连接点）‌。 二、状态转移逻辑 ‌1.初始化状态‌ 设置 st[0][1]=0，表示第 0 步时节点 1 可达‌。 ‌2.动态填充状态矩阵‌ 双重循环遍历步数 i（1 到 100）和节点 j（1 到 n）。 变量 len 控制有效步数衰减：每次迭代 len=max(len-1,0)，若 len>0 则标记当前节点可达性‌。 关键条件：若前一步 st[i-1][t] 有效且非当前节点 j，则重置 len=k，实现步数续传‌。 三、查询处理 对每个查询 (x,y)，检查 st[x][y] 是否为非 -1 值，若不等于 -1，输出 1（表示任务可以完成）。否则，输出  0（表示任务不能完成）。 【算法代码】

#include <bits/stdc++.h>
using namespace std;

const int N=2e5+5;
const int M=1e2+5;
vector<int> v[N];
int st[M][N];
int T,n,k,q;

int main() {
cin>>T;
while(T–) {
memset(st,-1,sizeof st);
scanf("%d%d%d",&n,&k,&q);
for(int i=1; i<=n; i++) {
v[i].clear();
int len;
scanf("%d",&len);
for(int j=1; j<=len; j++) {
int t;
scanf("%d",&t);
v[i].push_back(t);
}
}

st[0][1]=0;
for(int i=1; i<=100; i++) {
for(int j=1; j<=n; j++) {
int len=0;
for(auto t:v[j]) {
len=max(len-1,0);
if(len) {
if(st[i][t]==-1) st[i][t]=j;
else if(st[i][t] && st[i][t]!=j) st[i][t]=0;
}
if(st[i-1][t]!=-1 && st[i-1][t]!=j) len=k;
}
}
}

while(q–) {
int x,y;
scanf("%d%d",&x,&y);
if(st[x][y]!=-1) cout<<1<<endl;
else cout<<0<<endl;
}
}

return 0;
}

/*
in:
1
3 3 7
5 1 2 3 4 1
3 1 2 5
3 5 1 6
1 2
1 4
2 4
3 4
6 6
1 1
7 7

out:
1
0
1
0
1
0
0
*/

【参考文献】 https://www.luogu.com.cn/problem/solution/P11230