【图论】最短路问题

单源最短路问题

单源最短路问题是指固定一个起点，求它到其他任意一点的最短路问题。

Dijkstra算法（迪克斯拉特算法）

首先要注意的是，这个算法仅仅用于图中没有负边的情况。

原理

Dijkstra本质逻辑其实是动态规划，我们要求任意点i到起点（假设为1）的距离，我们不妨用一个数组dist记录这一距离，即dist[i]为1->i的最短路距离，所以现在我们需要考虑的问题就是如何更新并求得dist，这一部分就是算法的重点。

我们将图的点分为两个集合，集合A为最短路径已经确定的点，集合B为最短路径尚未确定的点。

每一次我们从B中选取dist最小的点（设为x），将他转移到A中，同时我们利用x的dist来更新x的邻居（设为p）的dist，即

dist[p]=min(dist[p],dist[x]+e(x,p))//e(x,p)为边xp的权值

通过反复进行B->A操作，最终得到全部的dist，没看懂没关系，我们用图来演示一遍。

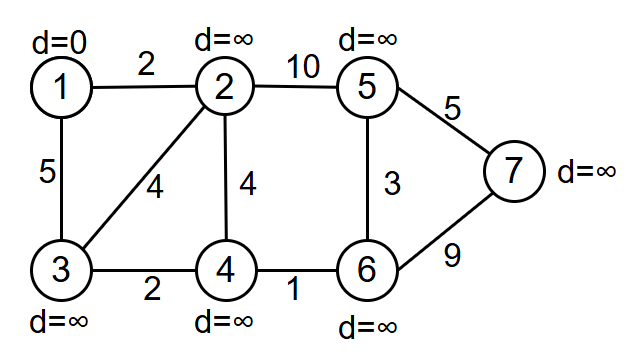
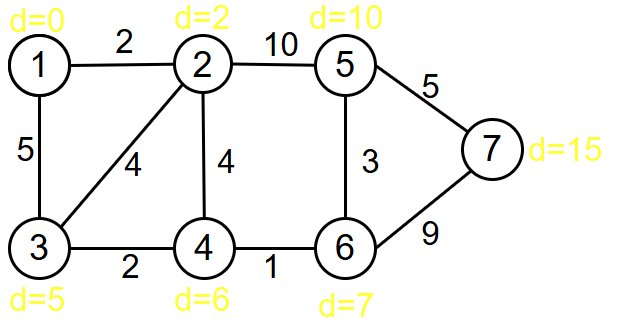
这是图的初始状态，dist简写为d，根据定义我们可得起点的d=0，而其他的dist我们全部设为一个极大的数，方便后续更新，此时我们选取1并入A，同时更新邻居的d值

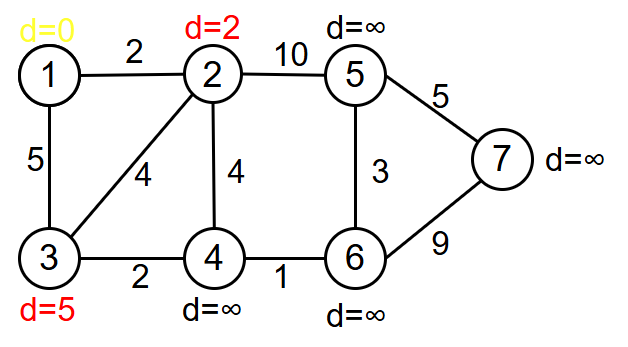
红色为这一次发生了更新的d，黄色为已经固定的d，也就是集合A中的元素。接下来我们在B中选择min进行更新，显然这次我们应该选择2，我们会进行如下更新

d[3]:5->5(d[2]+4>5)

d[4]:∞->d[2]+4=6

d[5]:∞->d[2]+10=12

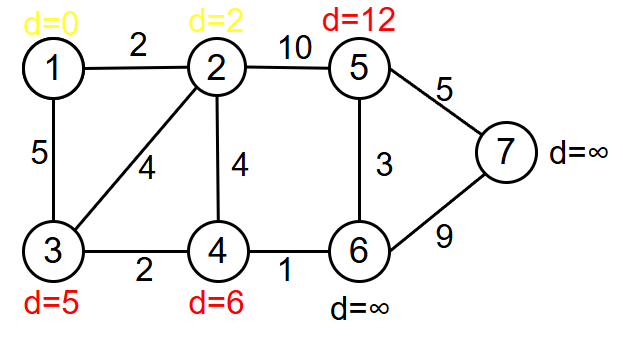
选择最小的d[3]

d[4]:6->6(d[3]+2>6)

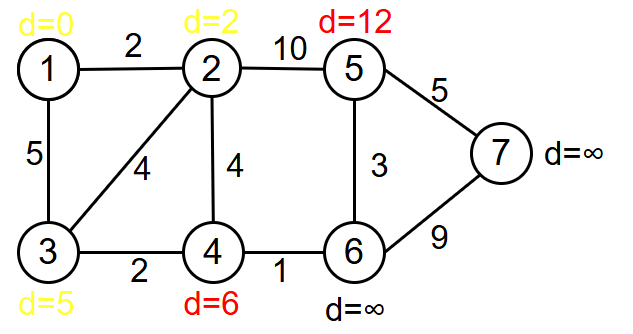
不断重复这一操作，最终使得全部d变成黄色，即全部并入集合A

朴素实现

const int INF=0x3f3f3f3f;
const int N=1e3+7;//上限
struct edge{
int to,w;
edge(int x,int y){to=x;w=y;}
};
vector<vector<edge>> g(N,vector<edge>());
//邻接表存储图，to为边的终点端，w为权值
bool vis[N];
int dist[N];
void dijkstra(int n,vector<vector<edge>>& g){
//n为图的点数,N>n
for(int i=1;i<=n;i++){
dist[i]=INF;
vis[i]=false;
}
dist[1]=0;
//初始化
while(true){
int v=-1;
for(int i=1;i<=n;i++){
if(vis[i]) continue;
if(v==-1||dist[i]<dist[v]) v=i;
}
if(v==-1) break;
//如果为-1代表全部都被标记，即B集合为空
vis[v]=true;
for(auto p:g[v])//更新操作
dist[p.to]=min(dist[p.to],dist[v]+p.w);
}
}

注意此处起点设为1，实际操作时我们可以按照要求修改起点。

最终实现复杂度为O(V²)

堆优化

可以发现，复杂度来源主要是最小dist的选取以及邻居的更新，邻居更新我们无法继续优化，但是最小dist的选取我们可以用最小堆进行优化。

最小堆我们选用STL中优先队列。

typedef pair<int,int> P;
const int INF=0x3f3f3f3f;
const int N=1e3+7;//上限
struct edge{
int to,w;
edge(int x,int y){to=x;w=y;}
};
vector<vector<edge>> g(N,vector<edge>());
//邻接表存储图，to为边的终点端，w为权值
bool vis[N];
int dist[N];
void dijkstra(int n,vector<vector<edge>>& g){
//n为图的点数,N>n
priority_queue< P,vector<P>,greater<P> > q;
//first是最短距离，sceond是点的编号
for(int i=1;i<=n;i++)
dist[i]=INF;
dist[1]=0;
q.push(P(0,1));
//初始化
while(!q.empty()){
P x=q.top();q.pop();
int v=x.second;
if(dist[v]<x.first) continue;
//如果x的距离大于dist[v]那就不能用它更新邻居
for(auto p:g[v]){
if(dist[p.to]>dist[v]+p.w){
dist[p.to]=dist[v]+p.w;
q.push(P(dist[p.to],p.to));
}
}
}
}

其实可以发现，我们在这里删除了vis数组，实际上，入队操作实现了这一作用，在更新过程中我们将发生更新的元素入队，也就是上文图中红色元素，而已经固定的黄色元素不会发生更新则被剔除，借此实现了vis数组的功能。

最终实现O(ElogV)。

Bellman-Ford算法（贝尔曼福特算法）

相比于迪克斯拉特算法，这一算法可以处理负边的情况。

原理

基本原理

这个原理特别简单，我们维护一个数组d，d[i]代表了从起点s到点i的最短路径，那么我们得到

d[i]=min{d[j]+e(j,i)}//e(j,i)为j到i的权值

如果是DAG（有向无环图）我们就可以按照拓扑序遍历。但如果有环，如果不是负环，这也并不影响算法运作，如果有负环这就是我们需要着重考虑的部分了。

负环：环上所有的边权和为负数。

如果有负环，我们将一条最短路径简化成三个点

起点——>负环——>终点

由于负环的权值为负，所以起点到终点的距离可以无限小，因为每走一次负环距离都会缩短（有点神奇不是吗），实现起来就是

起点——>负环环环环环环……..——>终点

负环处理原理

所以我们需要检测是否存在负环，有负环就无解（最短路可以无穷小）。

对于任意有V个顶点的图，起点到终点的最短路最多经过（v-1)条边，因为最短路不会同时经过同一顶点两次，除了一种情况，就是负环。因为对于负环来说，经过同一顶点的代价是负的。我们就可以借助这一特性来检测负环。

实现

struct edge{
int from,to,w;
};
vector<edge> g;//我们选择记录边
int V,E,s;//顶点数，边数，起点数
int d[MAXV];
bool check(){
for(int i=1;i<=V;i++) d[i]=0;//初始化为0，为了应对负边
for(int i=1;i<=V;i++){
for(int j=1;j<=E;j++){
edge e=g[j];
if(d[e.to]>d[e.from]+e.w){
d[e.to]=d[e.from]+e.w;
if(i==V) return false;
//如果第V次都更新了，就代表有负环，因为正常图最多更新V-1次
}
}
}
return true;
}
void Bellman(){
for(int i=1;i<=V;i++) d[i]=INF;
d[s]=0;
while(true){
bool update=false;
for(int i=1;i<=E;i++){
edge e=g[i];
if(d[e.from]!=INF&&d[e.to]>d[e.from]+e.w){
d[e.to]=d[e.from]+e.w;
update=true;
}
}
if(!update) break;
}
}

由于while最多循环（V-1）次所以实现为O(V²)

任意两点最短路问题

Floyd-Warshall算法（弗洛伊德-沃舍尔）

对于任意两点的问题，我们用Floyd算法来解决，本质是动态规划。

原理

我们定义状态  f[k][i][j]  ,表示为在只使用编号1-k的顶点当作中间节点的情况下，i到j的最短路。

而f[0][i][j]则代表e(i,j)，没有就设为无穷大。

所以我们就可以把只用1-k顶点的问题约束到只用1-k-1顶点的问题中

对于顶点k，我们有两种情况，经过k，不经过k，于是我们就可以得到状态转移方程

f[k][i][j] = min( f[k-1][i][j] , f[k-1][i][k] + f[k-1][k][j] )

实际操作中，由于第一维不会影响算法进行，我们可以去掉第一位减小空间开销。

而Floyd对于负环处理比较简单，只需要检测e(i,j)是否小于0即可，这里不再展示。

实现

struct edge{
int from,to,w;
};
int n,E;//点数，边数
int f[N][N];
void init(){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
f[N][N]=INF;
}
}
for(int i=1;i<=E;i++){
int u,v;cin>>u>>v;
cin>>f[u][v];
}
}
void Floyd(){
for(int k=1;k<=n;k++){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
f[i][j]=min(f[i][j],f[i][k]+f[k][j]);
}
}
}
}

最终实现O(n³)