网硕互联帮助中心双指针
引言
其实对于双指针它不太像一种前缀和与差分有固定的公式，它更像是一种思想，它不是我去给你说一个公式你就能掌握，而是像我们高中一样去刷题，掌握它的各种变式，所以这篇博客我将会举一些题目然后你去看题目，去掌握这种思想
第一种分类
顾名思义双指针就是有两个指针进行移动，其主要的分类为对撞指针和快慢指针 对撞指针就是两个指针相向移动 快慢指针就是两个指针同向移动只不过一个在前一个在后 一般来说我们都会有一个先移动的指针，一个后移动的指针
第二种分类
我们对于双指针问题还有一种分类方式就是根据序列的个数来分类 一个序列：类似快速排序 两个序列：类似归并排序
模板
for(int i = 0, j = 0; i < n; i++){//i j 的初始化与i的截止范围
while(j < i && check(i, j){//i 指针移动条件与截止范围
j++;
}
}
一般思路
一般我们会写一个复杂度为
O
(
n
2
)
O(n^2)
O(n2) 的两个指针再优化成复杂度为
O
(
n
)
O(n)
O(n) 的双指针
题目
1. 最长连续不重复子序列（AcWing 799）
AcWing 799 给定一个长度为
n
n
n 的整数序列，请找出最长的不包含重复的数的连续区间，输出它的长度
输入格式 第一行包含整数
n
n
n 第二行包含
n
n
n 个整数（均在
0
∼
10
5
0∼10^5
0∼105 范围内，表示整数序列
输出格式 共一行，包含一个整数，表示最长的不包含重复的数的连续区间的长度。
数据范围
1
≤
n
≤
10
5
1\\le n \\le 10^5
1≤n≤105
输入样例：
5
1 2 2 3 5
输出样例：
3
1.1 一般思路
我们定义一个计数器数组
c
o
u
n
t
[
]
count[]
count[]
c
o
u
n
t
[
a
[
i
]
]
count[a[i]]
count[a[i]] 表示
a
[
i
]
a[i]
a[i] 这个数字出现的次数
#include<bits/stdc++.h>
using namespace std;
const int n = 1010;
int a[N],count[N];
int main(){
int n;
cin >> n;
for(int i = 0; i < n; i++){
cin >>a[i];
count[a[i]]++;
}
}
c
o
u
n
t
[
]
count[]
count[] 用来统计数字出现次数 定义
i
,
j
i,j
i,j 指针指向数组的首位置 一开始我们向右移动
i
i
i 指针并统计
i
i
i 指向的的数字在
[
j
,
i
]
[j,i]
[j,i] 这个区间的出现次数，此时
c
o
u
n
t
[
a
[
i
]
]
+
+
count[a[i]]++
count[a[i]]++ 当某个数出现第二次时我们停止
i
i
i 指针，开始移动
j
j
j 指针，此时
c
o
u
n
t
[
a
[
j
]
]
−
−
count[a[j]]–
count[a[j]]−− 一直到指向与
i
i
i 停止时指向的元素，将将其在
[
j
,
i
]
[j,i]
[j,i] 区间出现的次数减为
1
1
1 我们继续移动
i
i
i 知道它停止 注意每次在
i
i
i 指针停止时我们将答案判断大小一次 题目代码
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int a[N], count[N];
int main(){
int n;
cin >> n;
for(int i = 0; i < n; i++)cin >> a[i];
int ans = 0;
for(int i = 0, j = 0; i < n; i++){
count[a[i]]++;
while(count[a[i]] > 1){
count[a[j]]—;
j++;
}
ans = max(ans, i – j + 1);
}
return 0;
}
1.2 图解
i = 0, j = 0 
i++ 
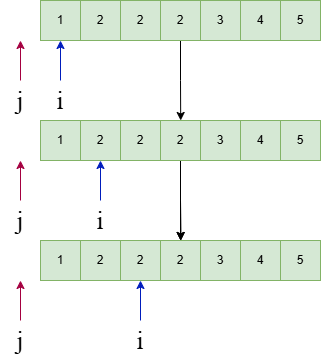j++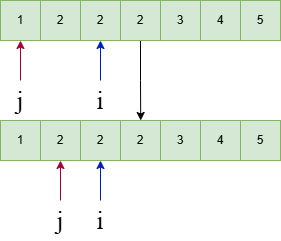 
i++后j++就是说当如果在一个相等的区间内
i
i
i 移动之后
j
j
j 也会紧接着移动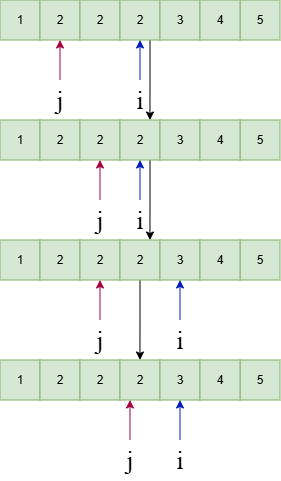i 
i++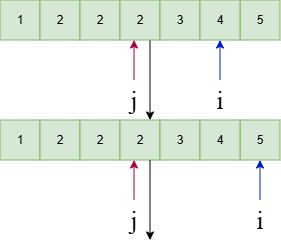 
2. 连续正整数和 (Luogu P1147)
Luogu P1147
给定一个正整数
M
M
M，求出所有的连续的正整数段（每一段至少有两个数），使得这些连续的正整数段中的全部数之和为
M
M
M。
例如，
1998
+
1999
+
2000
+
2001
+
2002
=
10000
1998+1999+2000+2001+2002=10000
1998+1999+2000+2001+2002=10000，所以从
1998
1998
1998 到
2002
2002
2002 的一个正整数段为
M
=
10000
M=10000
M=10000 的一个解。
输入格式
输入一行一个正整数，表示
M
M
M 的值（
10
≤
M
≤
2
×
10
6
10\\le M\\le 2\\times 10^6
10≤M≤2×106）。
输出格式
输出每行包含两个正整数，表示一个满足条件的连续正整数段的左右端点，两数之间用一个空格隔开。
输出按左端点大小升序排列。
输入
10000
输出
18 142
297 328
388 412
1998 2002
2.1 一般思路
定义
i
i
i 指针开始向右移动 定义
s
u
m
=
a
j
+
a
j
+
1
+
⋯
+
a
i
sum =a_j +a_{j+1}+\\dots+a_i
sum=aj+aj+1+⋯+ai 如果
s
u
m
=
m
sum=m
sum=m 我们就输出此时的
i
,
j
i,j
i,j 如果
s
u
m
<
m
sum < m
sum<m 我们就
i
i
i 指针右移动，此时
s
u
m
sum
sum 会增大 如果
s
u
m
>
m
sum > m
sum>m 我们就
j
j
j 指针右移动，此时
s
u
m
sum
sum 会减小 注意输出放在前面
#include<bits/stdc++.h>
using namespace std;
const int N = 2e6 + 10;
int a[N], count[N];
int main(){
int m;
cin >> m;
int sum = 0;
int i = 1, j = 1;
while(i < m / 2 ){
if(sum < m){
sum += i;
i++;
}
while(j < i && sum >= m){
if(sum == m) printf("%d %d\\n", j, i);
sum -= j;
j++;
}
}
}
3. 数组元素的目标和 (AcWing 800)
AcWing 800 给定两个升序排序的有序数组
A
A
A 和
B
B
B ，以及一个目标值
x
x
x 数组下标从
0
0
0 开始 请你求出满足
A
[
i
]
+
B
[
j
]
=
x
A[i]+B[j]=x
A[i]+B[j]=x 的数对
(
i
,
j
)
(i,j)
(i,j) 数据保证有唯一解。
输入格式 第一行包含三个整数
n
,
m
,
x
n,m,x
n,m,x，分别表示
A
A
A 的长度，
B
B
B 的长度以及目标值
x
x
x 第二行包含
n
n
n 个整数，表示数组
A
A
A 第三行包含
m
m
m 个整数，表示数组
B
B
B
输出格式 共一行，包含两个整数
i
i
i 和
j
j
j
数据范围 数组长度不超过
10
5
10^5
105 同一数组内元素各不相同。
1
≤
数组元素
≤
10
9
1≤数组元素≤10^9
1≤数组元素≤109
输入样例：
4 5 6
1 2 4 7
3 4 6 8 9
输出样例：
1 1
3. 1 一般思路
一般来说，我们对于这道题会考虑 将
i
i
i 指针指向在
a
[
]
a[ ]
a[] 数组里面第一个元素 将
j
j
j 指针指向在
b
[
]
b[ ]
b[]数组里面最后一个元素 如果
a
[
i
]
+
b
[
j
]
=
x
a[i] + b[j]=x
a[i]+b[j]=x 我们就输出 如果
a
[
i
]
+
b
[
j
]
<
x
a[i] + b[j]<x
a[i]+b[j]<x 我们就让
i
i
i 指针右移动 如果
a
[
i
]
+
b
[
j
]
>
x
a[i] + b[j]>x
a[i]+b[j]>x 我们就让
j
j
j 指针左移动
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int a[N],b[N];
int main(){
int n, m, x;
cin >> n >> m >> x;
for(int i = 0; i < n; i++) cin >> a[i];
for(int i = 0; i < m; i++) cin >> b[i];
int i = 0, j = m – 1;
while(i < n && j >= 0){
if(a[i] + b[j] == x) {
printf("%d %d", i, j);
i++;
j—;
break;
}
else if(a[i] + b[j] < x) i++;
else j—;
}
}
总结
一般我们是
i, j 初始化
while(i的范围 && j的范围){
if(条件){输出(可能会有移动)}
else if(i移动条件) i的移动;
else j的移动;
}
也可以是
for(i, j初始化; 快指针范围; 快指针移动){
if(慢指针的范围 && 慢指针移动的条件){
慢指针的移动;
}
if(输出条件){
输出
}
}
但是无论是怎样的格式，我们主要学的是这种思想
练习题
AcWing 2816. 判断子序列 代码
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int a[N], b[N];
int main(){
int n, m;
cin >> n >> m;
for(int i = 0; i < n; i++) cin >> a[i];
for(int i = 0; i < m; i++) cin >> b[i];
int i = 0, j = 0;
int s = 0;
while(i < n && j < m){
if(a[i] == b[j]){
i++;
j++;
s++;
}
else j++;
if(s == n){
printf("Yes");
return 0;
}
}
printf("No");
return 0;
}
评论前必须登录！
注册