三维前缀和与差分
By Zhang_HangWei
1. 三维前缀和
1.1 公式
s[x][y][z] = s[x–1][y][z] + s[x][y–1][z] + s[x][y][z–1] – s[x–1][y–1][z] – s[x–1][y][z–1] – s[x][y–1][z–1] + s[x–1][y–1][z–1] + a[x][y][z]
1.2 公式理解
s[x][y][z]
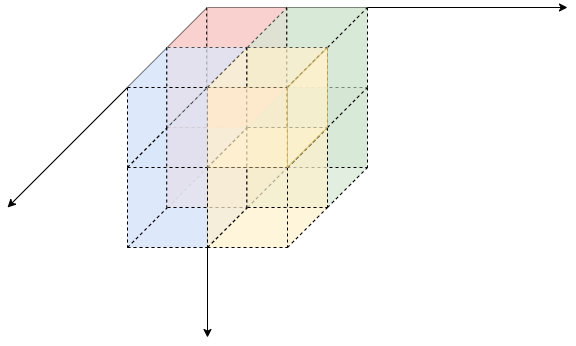
s[x-1][y][z]
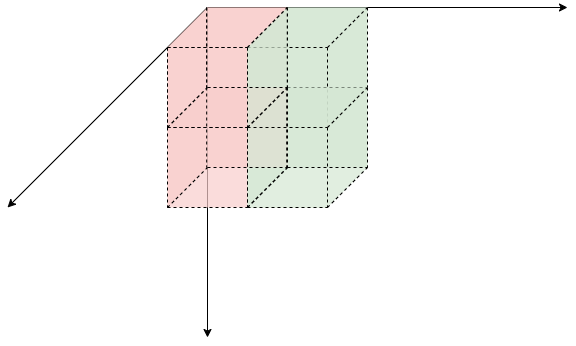
s[x][y-1][z]
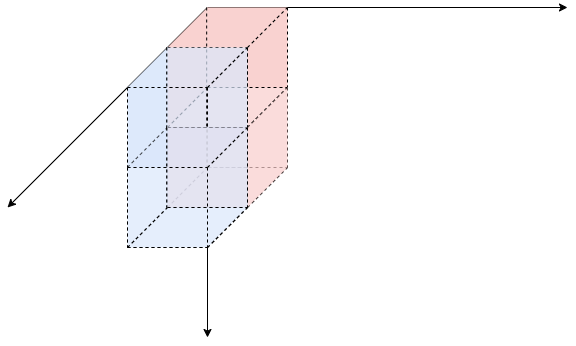
s[x][y][z-1]
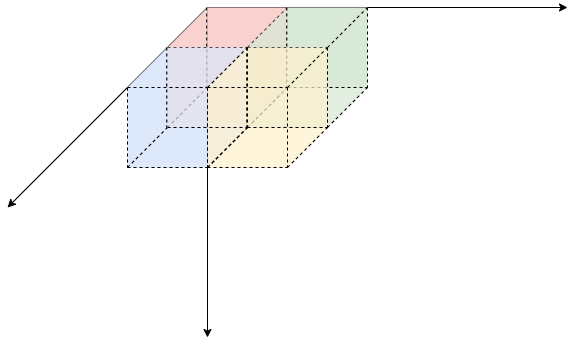
s[x-1][y-1][z]
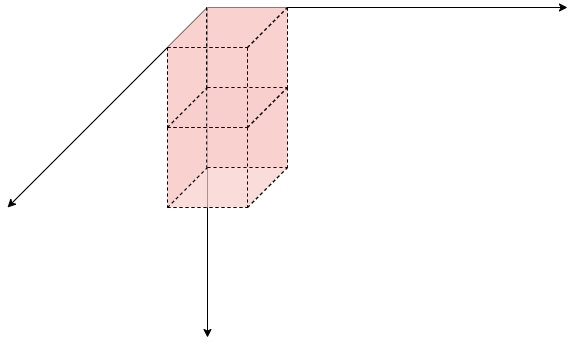
s[x-1][y][z-1]
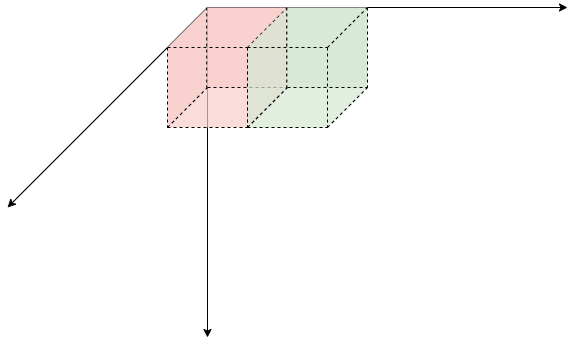
s[x][y-1][z-1]
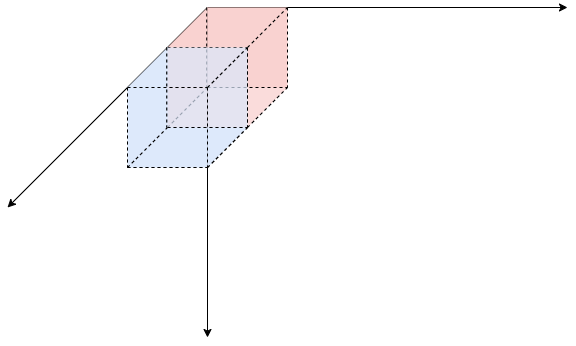
s[x-1][y-1][z-1]
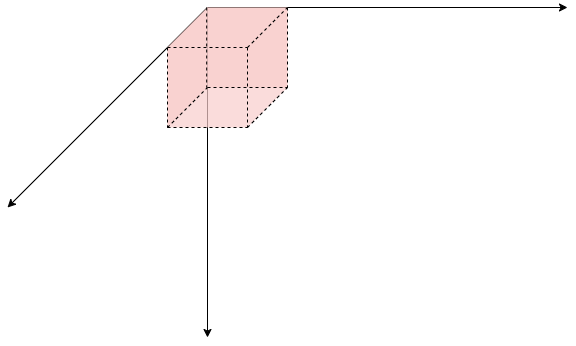
a[x][y][z]
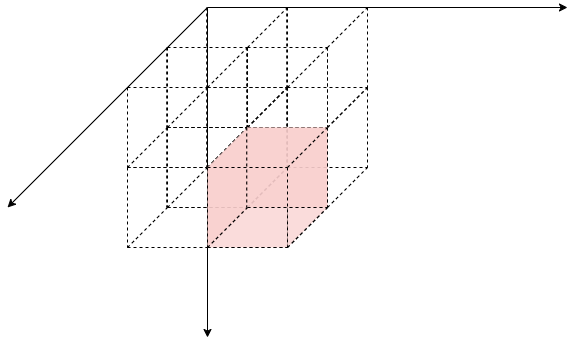
通过以上操作我们得到前缀和s[x][y][z]
1.3 应用:求子立方体和
我们计算整个红色立方体中蓝色立方体里的数字和(每个小立方体内存有一个数字)
毕竟是三维数组嘛!
蓝色立方体是红色立方体的子立方体
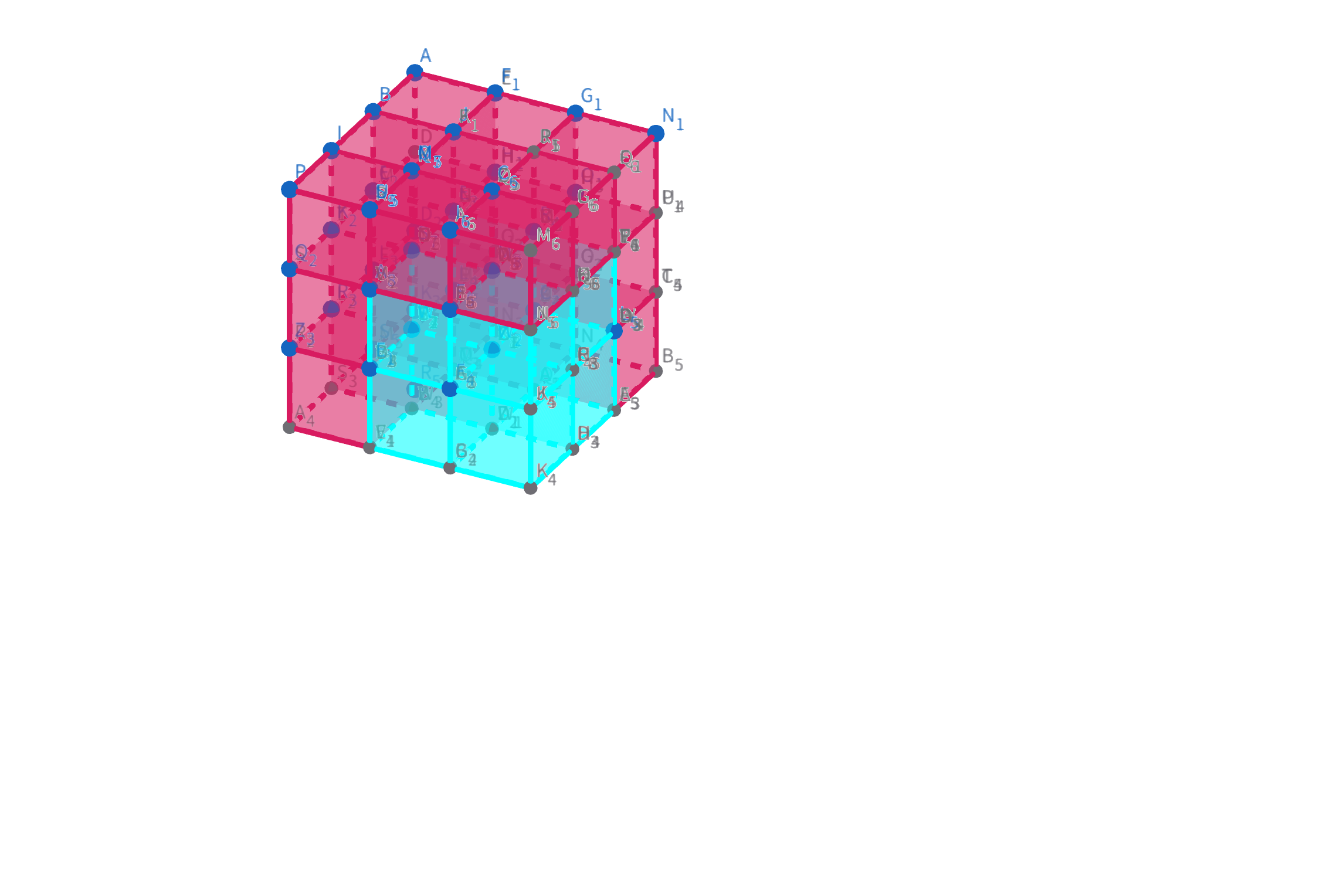
其中 (x1,y1,z1)(x_1,y_1,z_1)(x1,y1,z1) 与 (x2,y2,z2)(x_2,y_2,z_2)(x2,y2,z2) 为立方体的左上角与右下角
公式
sum = s[x2][y2][z2] – s[x2][y2][z1–1] – s[x2][y1–1][z2] – s[x1–1][y2][z2] + s[x1–1][y1–2][z2] + s[x1–1][y2][z1–1] + s[x2][y1–1][z1–1] – s[x1–1][y1–1][z1–1]
图示
s[x2][y2][z2]
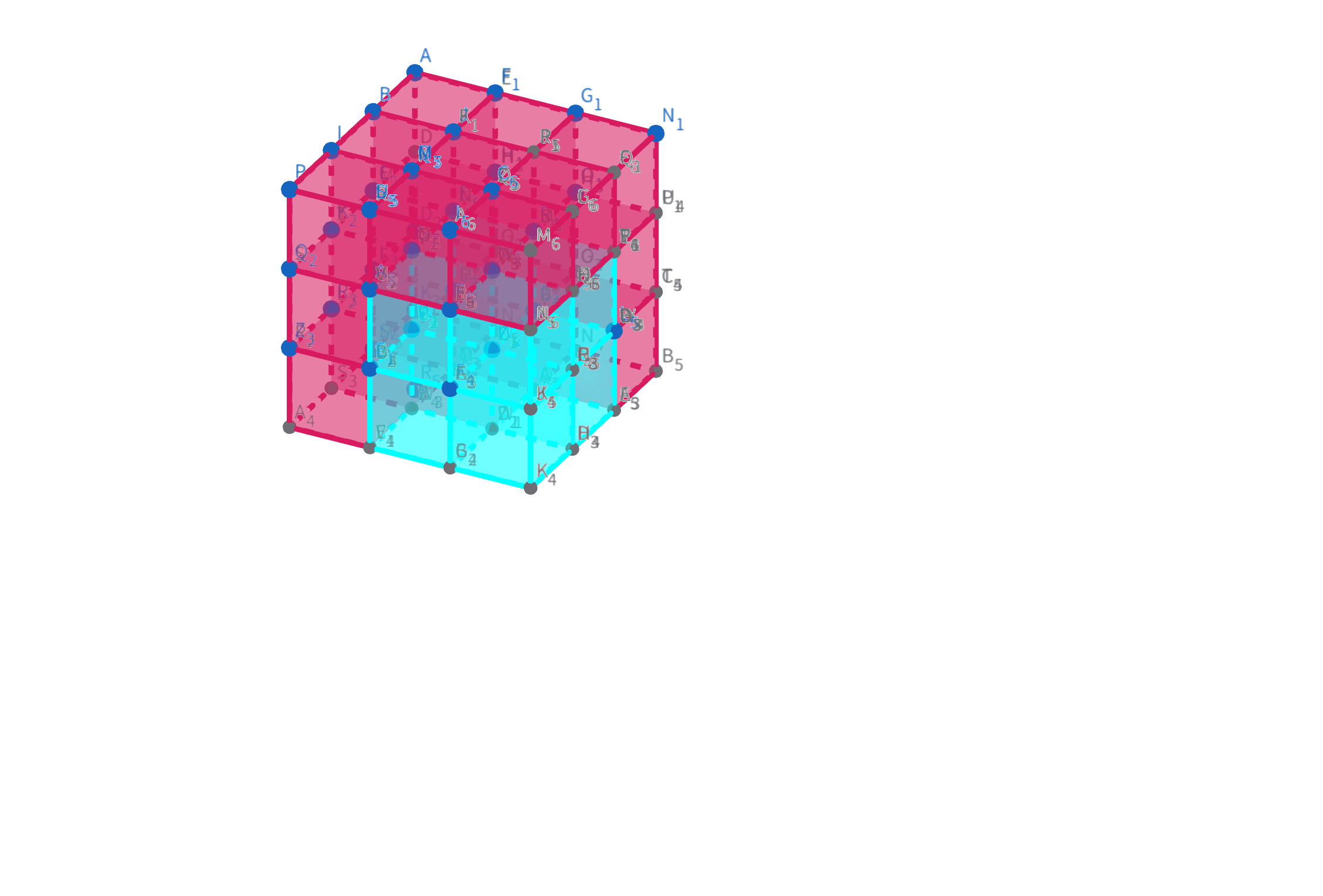
都是以 BBB 为原点向左建立 xxx 轴,向右建立 yyy 轴,向下建立 zzz 轴
s[x2][y2][z1-1]这是最上面一层
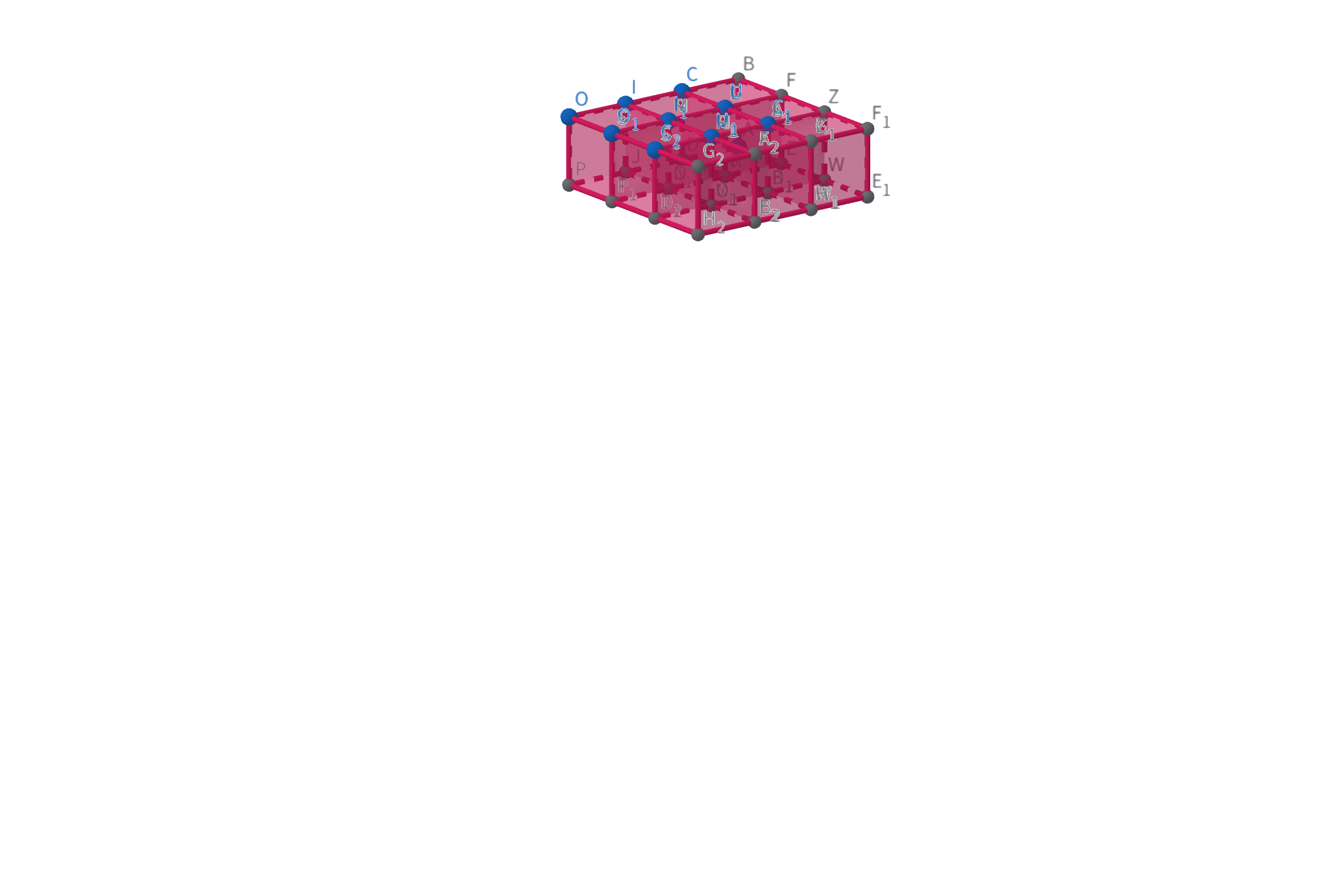
s[x2][y1-1][z2]这是 y−zy-zy−z 那一面

s[x1-1][y2][z2]这是 x−zx-zx−z 那一面

s[x1-1][y1-2][z2]这是zzz 轴上的

s[x1-1][y2][z1-1] y−zy-zy−z 面最上的

s[x2][y1-1][z1-1]

s[x1-1][y1-1][z1-1]蓝色立方体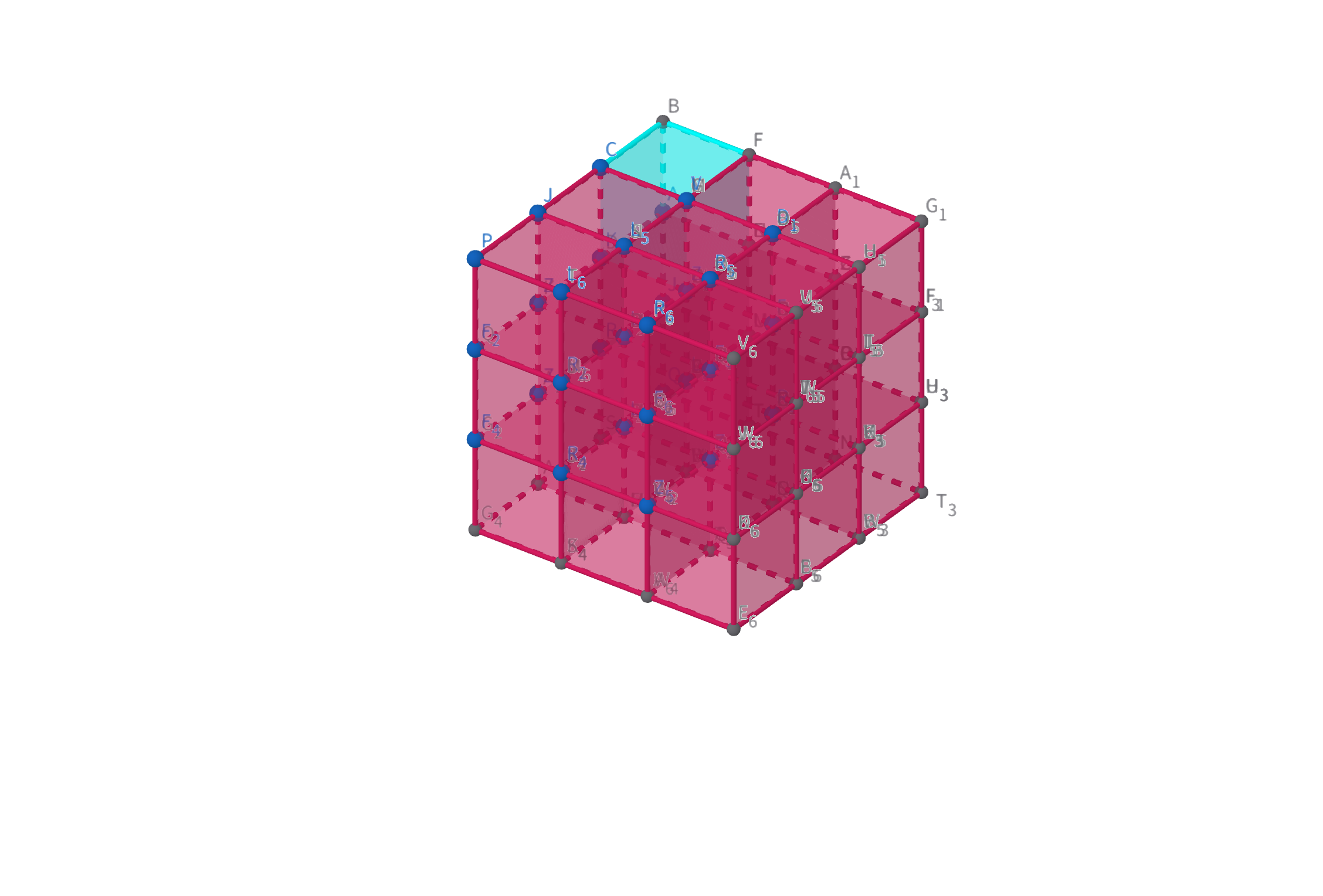
2. 三维差分
2.1 子立方体加数
这里对差分的介绍我们仍然是先介绍子立方体加数,特殊的子立方体加数的三维差分
首先我们对a[x][y][z]加上 CCC 就是对s[x][y][z]右下角的每个s[][][]数组加 CCC
这里我们对子立方体 (x1,y1,z1)(x_1,y_1,z_1)(x1,y1,z1), (x2,y2,z2)(x_2,y_2,z_2)(x2,y2,z2) 加上 CCC
蓝色部分加上 CCC
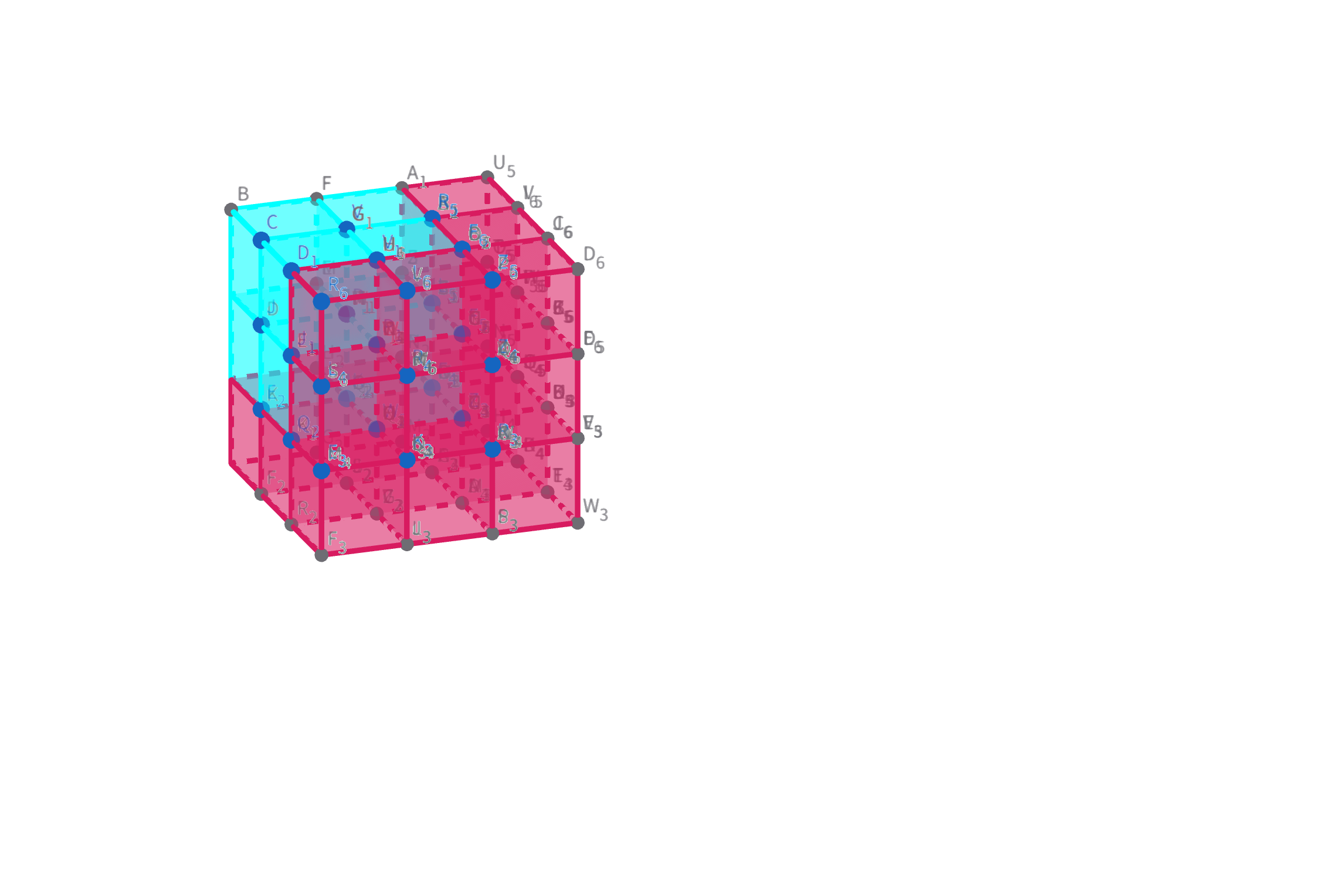
公式
a[x1][y1][z1] += c;
a[x1][y1][x2 + 1] -= c;
a[x1][y2 + 1][z1] -= c;
a[x2 + 1][y1][z1] -= c;
a[x1][y2 + 1][z2 + 1] += c;
a[x2 + 1][y1][z2 + 1] += c;
a[x2 + 1][y2 + 1][z1] += c;
a[x2 + 1][y2 + 1][z2 + 1] -= c;
2.2 差分
当 x1=x2,y1=y2,z1=z2x_1 = x_2,y_1 = y_2, z_1= z_2x1=x2,y1=y2,z1=z2 是用以上公式就是差分
 网硕互联帮助中心
网硕互联帮助中心





评论前必须登录!
注册