题目描述
Bessie 搬到了一个小农场,有时喜欢回去拜访她的一个好朋友。她不想太快到达她的旧家,因为她喜欢沿途的风景。她决定选择第二短的路径而不是最短的路径。她知道一定存在某条第二短路径。
乡村由 R(1≤R≤100,000) 条双向道路组成,每条道路连接 N(1≤N≤5000) 个交叉路口中的两个,这些交叉路口被方便地编号为 1 到 N。Bessie 从交叉路口 1 出发,她的朋友(目的地)在交叉路口 N。
第二短路径可以与任何最短路径共享道路,并且可以回溯,即多次使用相同的道路或交叉路口。第二短路径是长度比最短路径长的最短路径(即,如果存在两条或多条最短路径,第二短路径是长度比这些路径长但不比任何其他路径长的路径)。
输入格式
第 1 行:两个用空格分隔的整数:N 和 R。
第 2 行到第 R+1 行:每行包含三个用空格分隔的整数:A、B 和 D,描述连接交叉路口 A 和 B 的一条长度为 D(1≤D≤5000) 的道路。
输出格式
第 1 行:节点 1 和节点 N 之间第二短路径的长度。
显示翻译
题意翻译
输入输出样例
输入 #1复制运行
4 4
1 2 100
2 4 200
2 3 250
3 4 100
输出 #1复制运行
450
说明/提示
两条路径:1→2→4(长度 100+200=300)和 1→2→3→4(长度 100+250+100=450)。
(由 ChatGPT 4o 翻译)
1. 题目重述
题目名称:Roadblocks (USACO 06 NOV)
核心问题:给定一张N个点、R条边的双向图,求从起点1到终点N的严格次短路径长度。
定义:严格次短路径是指长度严格大于最短路径长度的所有路径中,长度最小的那一条。
-
数据范围:
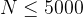 ,
,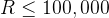 。
。 -
特殊说明:路径可以包含重复的节点或边(即允许走回头路)。
2. 题目分析
误区:K 短路算法?
一听到“第 K 短路”,很多人第一反应是 A* 算法。虽然 A* 可以解,但对于K=2且图比较简单的情况,A* 写起来太繁琐且容易出错。
正解:Dijkstra 状态拆分
普通的 Dijkstra 维护一个 dis[i] 表示起点到i的最短距离。
为了求次短路,我们只需要让每个节点多维护一个状态。
状态定义:
-
dis[i][0]:起点到i的最短路长度。
-
dis[i][1]:起点到i的严格次短路长度。
初始化:
-
dis[1][0]=0,其余全为
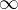 。
。
松弛操作(核心逻辑):
假设当前从点u拿出的距离是d,准备通过边权w更新邻居v,新距离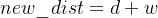 。
。
更新最短路:
如果 ![$new\\_dist < dis[v][0]$](https://www.wsisp.com/helps/wp-content/uploads/2026/01/20260127140916-6978c70cd28f3.png) :
:
-
原有的最短路
![$dis[v][0]$](https://www.wsisp.com/helps/wp-content/uploads/2026/01/20260127140916-6978c70ce0f4a.png) 沦为次短路,赋值给
沦为次短路,赋值给![$dis[v][1]$](https://www.wsisp.com/helps/wp-content/uploads/2026/01/20260127140916-6978c70ceec82.png) ,并加入队列。
,并加入队列。 -
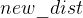 成为新的最短路,赋值给
成为新的最短路,赋值给![$dis[v][0]$](https://www.wsisp.com/helps/wp-content/uploads/2026/01/20260127140916-6978c70ce0f4a.png) ,并加入队列。
,并加入队列。
更新次短路:
如果![$new\\_dist > dis[v][0]$](https://www.wsisp.com/helps/wp-content/uploads/2026/01/20260127140917-6978c70d105ac.png) 且
且![$new\\_dist < dis[v][1]$](https://www.wsisp.com/helps/wp-content/uploads/2026/01/20260127140917-6978c70d1c38f.png) :
:
-
说明找到了一条比最短路长、但比旧次短路短的路径。
-
更新
![$dis[v][1] = new\\_dist$](https://www.wsisp.com/helps/wp-content/uploads/2026/01/20260127140917-6978c70d282b3.png) ,并加入队列。
,并加入队列。
等于最短路:
如果![$new\\_dist == dis[v][0]$](https://www.wsisp.com/helps/wp-content/uploads/2026/01/20260127140917-6978c70d3422f.png) :
:
-
题目要求严格次短,所以相等的路径对次短路没有贡献,直接忽略。
3. 完整代码
//严格次短路 邻接表+堆优化Dijkstra 时间复杂度:O(Rlog N)
#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>//对应min函数
using namespace std;
const int maxn=5010;
const int maxm=200010;
int dis[maxn][2];//dis[i][0]代表起点到i点的最短路 dis[i][1]代表次短路
int h[maxn];//存所有点的头指针
int vtex[maxm];//存第i条边终点下标
int nxt[maxm];//与第i条边同起点的下一条边的索引
int wt[maxm];//第i条边长度
int idx;//总边数
int n,r;
int vis[maxn];//记录每个点是否已经出队过
struct node{
int id;//点编号
int w;//点到起点距离(不管最短还是次短)
//优先队列默认最大堆,重载运算符修改为最小堆
friend bool operator <(node a,node b){
return a.w>b.w;
}
};
priority_queue<node> q;
void addedge(int u,int v,int w){
vtex[idx]=v;
nxt[idx]=h[u];
wt[idx]=w;
h[u]=idx++;
}
void dijkstra(){
dis[1][0]=0;//起点到自己的最短距离为0
node tmp;
tmp.id=1;
tmp.w=0;
q.push(tmp);//起点入队
while(!q.empty()){
tmp=q.top();//访问队首
q.pop();//队首出队
int nid=tmp.id;
//如果出队的tmp到起点的距离的距离大于tmp当前存储的到起点的次短路的距离 就跳过
//因为这个距离不可能用来更新tmp的邻接点
if(tmp.w>dis[tmp.id][1]) continue;
int p=h[nid];
while(p!=-1){//遍历tmp所有临接点
//如果邻接点到起点的最短路的距离大于经tmp去到起点的距离(情况1 发现比最短路更短的路径)
if(dis[vtex[p]][0]>tmp.w+wt[p]){
//就先把邻接点到起点的最短路的距离给到次短路
dis[vtex[p]][1]=dis[vtex[p]][0];
//然后再更新邻接点到起点的最短路的距离等于经tmp去到起点的距离
dis[vtex[p]][0]=tmp.w+wt[p];
//把最短距离和次短距离都入队
q.push({vtex[p],dis[vtex[p]][1]});
q.push({vtex[p],dis[vtex[p]][0]});
}
//如果邻接点到起点的最短路距离小于经tmp去到起点的距离 但是邻接点到起点的次短路距离大于经tmp去到起点的距离(情况2发现严格次短路径 (介于最短和次短之间))
else if(dis[vtex[p]][0]<tmp.w+wt[p] &&dis[vtex[p]][1]>tmp.w+wt[p]){
//就更新邻接点到起点的次短路距离等于经tmp去到起点的距离
dis[vtex[p]][1]=tmp.w+wt[p];
//然后入队
q.push({vtex[p],dis[vtex[p]][1]});
}
p=nxt[p];
}
}
}
int main(){
cin>>n>>r;//n个交叉路口 r条路
//初始化头指针数组为空
memset(h,-1,sizeof(h));
//初始化每个点到其他到起点的最短距离和次短距离都是无穷
memset(dis,0x3f,sizeof(dis));
//邻接表存图
for(int i=1;i<=r;i++){
int u,v,w;
cin>>u>>v>>w;
addedge(u,v,w);//双向道路 双向加边
addedge(v,u,w);
}
dijkstra();
//输出节点1和节点N之间第二短路径的长度
cout<<dis[n][1];
return 0;
}
4. 易错点总结
严格:题目中的定义决定了代码逻辑。如果是“非严格(允许相等)”,那么 new_dist > dis[v][0] 应该改为 new_dist>=dis[v][0] 或者在降级时逻辑会有变化。本题要求严格,所以相等的距离直接丢弃。
空间开销:由于是双向边,addedge 调用了两次,所以边的数组 (vtex, nxt, wt) 大小必须是 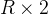 。只开100000会导致 RE。
。只开100000会导致 RE。
剪枝:if(d>dis[u][1]) continue; 这句非常重要。因为一个点可能会被多次入队,如果取出的距离比我们已经找到的次短路还长,它就不可能更新任何点的最短或次短路了。
 网硕互联帮助中心
网硕互联帮助中心


评论前必须登录!
注册