嵌入式开发学习———Linux环境下数据结构学习（五）

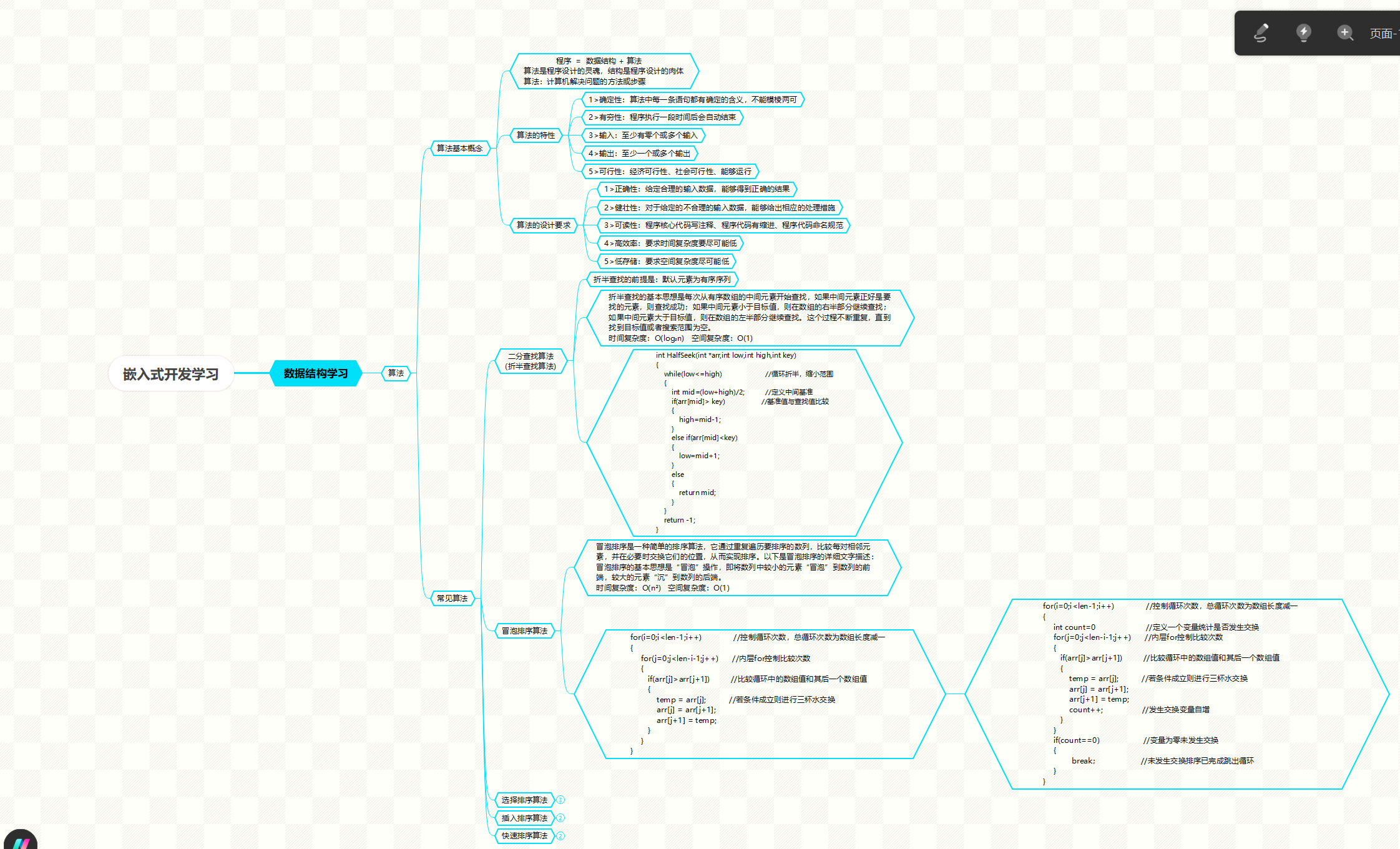
折半查找（二分查找）

适用于已排序的数组，通过不断缩小查找范围定位目标值。

int binarySearch(int arr[], int size, int target) {
int left = 0, right = size – 1;
while (left <= right) {
int mid = left + (right – left) / 2;
if (arr[mid] == target) return mid;
if (arr[mid] < target) left = mid + 1;
else right = mid – 1;
}
return -1; // 未找到
}

插入排序

将未排序元素逐个插入已排序部分的正确位置。

void insertionSort(int arr[], int size) {
for (int i = 1; i < size; i++) {
int key = arr[i], j = i – 1;
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j–;
}
arr[j + 1] = key;
}
}

快速排序

通过分治策略选取基准值，将数组分为左右两部分递归排序。

void swap(int *a, int *b) {
int temp = *a;
*a = *b;
*b = temp;
}

int partition(int arr[], int low, int high) {
int pivot = arr[high];
int i = low – 1;
for (int j = low; j < high; j++) {
if (arr[j] < pivot) {
i++;
swap(&arr[i], &arr[j]);
}
}
swap(&arr[i + 1], &arr[high]);
return i + 1;
}

void quickSort(int arr[], int low, int high) {
if (low < high) {
int pi = partition(arr, low, high);
quickSort(arr, low, pi – 1);
quickSort(arr, pi + 1, high);
}
}

关键点

• 折半查找要求数组有序，时间复杂度为 O(log n)。
• 插入排序适合小规模数据，时间复杂度为 O(n²)。
• 快速排序平均时间复杂度为 O(n log n)，需注意基准值选择。