2026-02-12:完成一个任务的最早时间。用go语言,给你一个二维整数数组 tasks,数组中每个元素 [s_i, t_i] 表示一个任务在时间点 s_i 开始,并需要 t_i 个时间单位才能结束。
请找出一个最小的时间点,使得在该时刻或之前至少有一个任务已经完成。
换句话说,求能首次出现任务完成的最早时间。
1 <= tasks.length <= 100。
tasks[i] = [si, ti]。
1 <= si, ti <= 100。
输入: tasks = [[1,6],[2,3]]。
输出: 5。
解释:
第一个任务从时间 t = 1 开始,并在 1 + 6 = 7 时完成。第二个任务在时间 t = 2 开始,并在 2 + 3 = 5 时完成。因此,最早完成的任务在时间 5。
题目来自力扣3683。
🔢 计算过程分步解析
初始化答案变量
程序首先将 ans 初始化为一个非常大的整数(math.MaxInt),确保任何任务的完成时间都会比这个初始值小,从而能被正确更新。
遍历任务数组
代码通过循环依次处理 tasks 中的每一个任务。对于当前任务 t,它包含两个元素:t[0] 是开始时间 s_i,t[1] 是持续时间 t_i。
计算单个任务的完成时间
对于每个任务,计算其完成时间:completionTime = t[0] + t[1]。
更新最早完成时间
将计算出的 completionTime 与当前记录的最小值 ans 进行比较。如果 completionTime 更小,则用这个更小的值更新 ans。这样,在遍历结束后,ans 保存的就是所有任务完成时间中的最小值。
返回结果
循环结束后,直接返回 ans 作为答案。
⏱️ 复杂度分析
-
时间复杂度:O(n)。
其中 n 是任务的数量(tasks.length)。算法只需要遍历任务数组一次,对每个任务执行常数时间(O(1))的操作(加法、比较),因此总时间复杂度与任务数量成线性关系。 -
空间复杂度:O(1)。
算法只使用了固定数量的额外变量(ans, 循环变量等),没有使用与输入数据规模(如任务数量 n)成正比的额外存储空间。
💎 总结
这个解决方案非常直接和高效。它抓住了问题的核心——任务的完成时间是其开始时间与持续时间之和,而最早完成时间就是所有完成时间中的最小值。通过一次遍历即可找到答案,无论在时间还是空间上都是最优的。
Go完整代码如下:
package main
import (
"fmt"
"math"
)
func earliestTime(tasks [][]int) int {
ans := math.MaxInt
for _, t := range tasks {
ans = min(ans, t[0]+t[1])
}
return ans
}
func main() {
tasks := [][]int{{1, 6}, {2, 3}}
result := earliestTime(tasks)
fmt.Println(result)
}
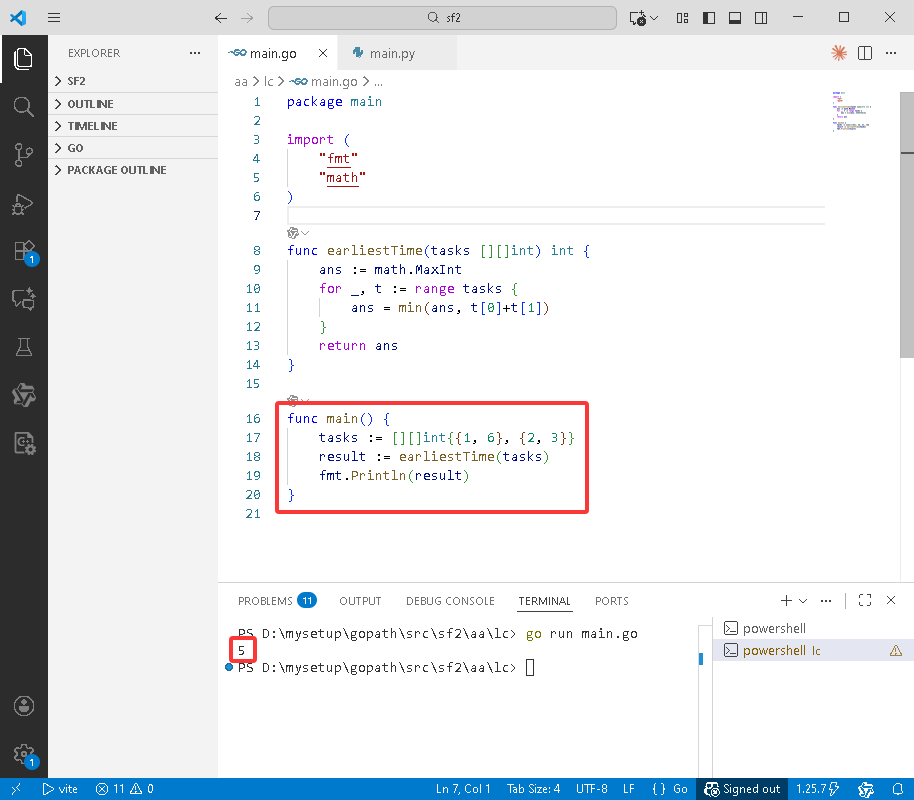
Python完整代码如下:
# -*-coding:utf-8-*-
from typing import List
def earliestTime(tasks: List[List[int]]) –> int:
ans = float('inf')
for t in tasks:
ans = min(ans, t[0] + t[1])
return ans
def main():
tasks = [[1, 6], [2, 3]]
result = earliestTime(tasks)
print(result)
if __name__ == "__main__":
main()
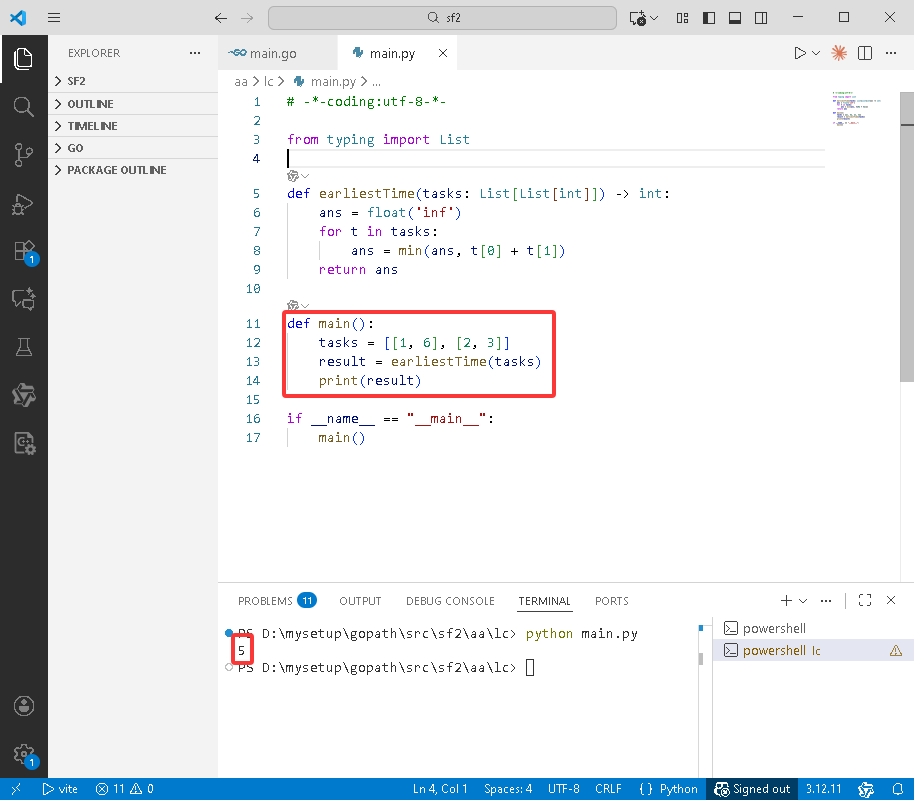
C++完整代码如下:
#include <iostream>
#include <vector>
#include <limits>
#include <algorithm>
using namespace std;
int earliestTime(vector<vector<int>>& tasks) {
int ans = numeric_limits<int>::max();
for (const auto& t : tasks) {
ans = min(ans, t[0] + t[1]);
}
return ans;
}
int main() {
vector<vector<int>> tasks = {{1, 6}, {2, 3}};
int result = earliestTime(tasks);
cout << result << endl;
return 0;
}
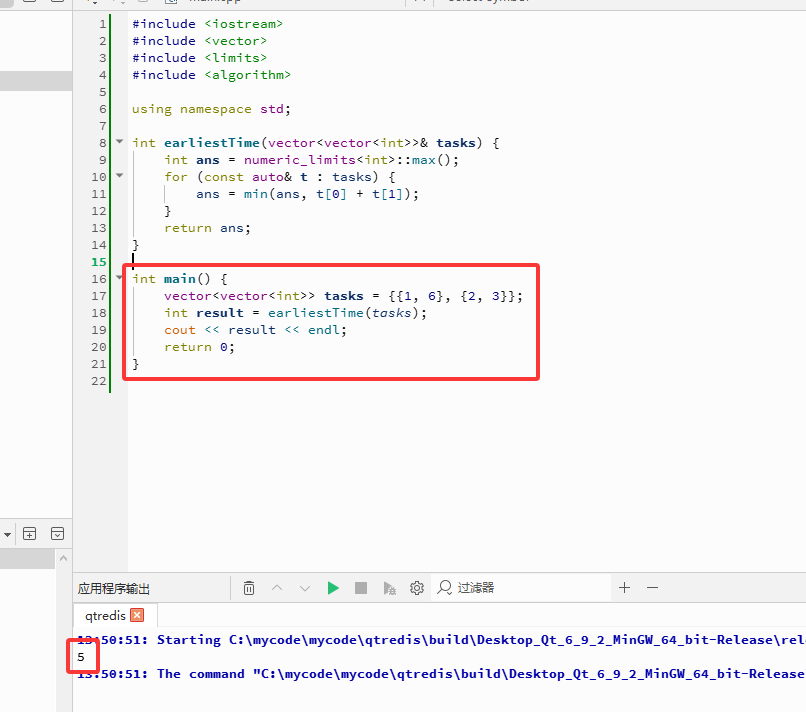
 网硕互联帮助中心
网硕互联帮助中心





评论前必须登录!
注册