数据结构:排序与算法

一、排序算法概述

排序算法是计算机科学中的基础算法，用于将一组数据按照特定顺序重新排列。排序算法的选择取决于数据规模、初始状态、稳定性要求及内存约束等因素。

二、五种排序算法的原理与性能分析

1. 冒泡排序（Bubble Sort）

· 工作原理：重复遍历待排序序列，依次比较相邻元素，若顺序错误则交换，直到没有元素需要交换为止

· 时间复杂度：

  · 最好情况：O(n)（已有序序列）

  · 最坏情况：O(n²)（完全逆序）

  · 平均情况：O(n²)

· 空间复杂度：O(1)（原地排序）

· 稳定性：稳定（相等元素不会交换位置）

· 适用场景：教学演示、小规模数据或近乎有序的数据

2. 选择排序（Selection Sort）

· 工作原理：每次从未排序部分选取最小（或最大）元素，与未排序部分的第一个元素交换，重复直到全部有序

· 时间复杂度：

  · 最好/最坏/平均情况均为 O(n²)

· 空间复杂度：O(1)

· 稳定性：不稳定（如序列[5, 8, 5, 2]中，第一个5与2交换后改变相对顺序）

· 特点：交换次数少，但比较次数固定为n(n-1)/2次

3. 插入排序（Insertion Sort）

· 工作原理：构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入

· 时间复杂度：

  · 最好情况：O(n)（已有序序列）

  · 最坏情况：O(n²)（完全逆序）

  · 平均情况：O(n²)

· 空间复杂度：O(1)

· 稳定性：稳定（元素从后向前比较，相等时不移动）

· 优势：对小规模或基本有序数据效率高

4. 希尔排序（Shell Sort）

· 工作原理：改进的插入排序，通过将原始列表分割为多个子序列（按增量序列）分别进行插入排序，逐步缩小增量直至为1

· 时间复杂度：

  · 依赖于增量序列的选择

  · 最坏情况：O(n²)（使用某些增量序列）

  · 平均情况：O(n log n) ~ O(n^(3/2))

· 空间复杂度：O(1)

· 稳定性：不稳定（跨越多个位置的元素移动可能破坏稳定性）

· 特点：首个突破O(n²)时间复杂度的排序算法

5. 快速排序（Quick Sort）

· 工作原理：分治策略

  1. 选取基准元素（pivot）

  2. 将序列分为两部分：小于基准和大于基准

  3. 递归地对两部分进行快速排序

· 时间复杂度：

  · 最好情况：O(n log n)（每次划分均衡）

  · 最坏情况：O(n²)（每次划分极不均衡）

  · 平均情况：O(n log n)

· 空间复杂度：O(log n)（递归调用栈深度）

· 稳定性：不稳定（元素交换可能破坏相对顺序）

· 优化策略：随机选择基准、三数取中法、小数组切换为插入排序

三、查找算法：折半查找

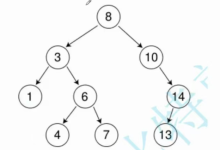
1. 折半查找（Binary Search）

· 前提条件：数据必须在有序数组中

· 工作原理：

  1. 确定查找范围的中间位置

  2. 比较中间元素与目标值

  3. 若相等则查找成功；若目标值小于中间元素，则在左半部分继续查找；否则在右半部分查找

  4. 重复上述步骤直至查找成功或范围为空

· 时间复杂度：O(log n)

· 空间复杂度：O(1)（迭代实现）或 O(log n)（递归实现）

· 稳定性：查找算法不涉及稳定性概念

· 特点：效率高但仅适用于有序静态数据

四、算法比较与选择建议

1. 时间复杂度对比

算法 最好情况 平均情况 最坏情况 空间复杂度

冒泡排序 O(n) O(n²) O(n²) O(1)

选择排序 O(n²) O(n²) O(n²) O(1)

插入排序 O(n) O(n²) O(n²) O(1)

希尔排序 O(n log n) 取决于增量序列 O(n²) O(1)

快速排序 O(n log n) O(n log n) O(n²) O(log n)

2. 稳定性分析

· 稳定排序：冒泡排序、插入排序

· 不稳定排序：选择排序、希尔排序、快速排序

3. 适用场景

· 小规模数据（n < 50）：插入排序简单高效

· 中等规模数据：希尔排序或快速排序

· 大规模数据：快速排序（需注意最坏情况优化）

· 数据基本有序：插入排序或冒泡排序

· 需要稳定排序：冒泡排序或插入排序

· 查找操作频繁：先排序（快速排序）后使用折半查找

五、C语言实现要点补充

1. 排序算法的实现技巧

· 冒泡排序可添加标志位优化，若某次遍历无交换则提前结束

· 快速排序应避免递归深度过大，可采用栈模拟递归

· 希尔排序的增量序列选择影响性能（常用：Hibbard序列、Sedgewick序列）

2. 折半查找的边界处理

· 注意整数溢出的风险：mid = (low + high) / 2 可改为 mid = low + (high – low) / 2

· 循环终止条件：low <= high

· 查找失败时返回适当标识（如-1）

3. 性能测试方法

· 使用不同规模数据测试（随机、有序、逆序）

· 记录实际运行时间对比理论复杂度

· 分析缓存局部性对算法性能的影响