KMP算法(Knuth-Morris-Pratt算法)是一种高效的字符串匹配算法,主要用于在一个主文本字符串中查找一个子串的出现位置。它的核心思想是利用已经部分匹配的信息,避免在匹配失败时重复比较之前已经匹配过的字符。
核心概念
部分匹配表(Partial Match Table):也称为“失败函数”或“next数组”,记录了子串中每个位置之前的子串的最长相同前缀和后缀的长度。这个表帮助算法在匹配失败时决定子串应该向右滑动多少位。
时间复杂度:KMP算法的时间复杂度是O(n + m),其中n是主文本字符串的长度,m是子串的长度。这比暴力匹配算法的O(n*m)要高效得多。
算法步骤
构建部分匹配表:
- 初始化一个数组next,长度为子串的长度。
- 遍历子串,对于每个位置i,计算从子串开始到i的子串的最长相同前缀和后缀的长度,存入next[i]。
匹配过程:
- 使用两个指针i和j,分别指向主文本和子串的当前比较位置。
- 如果字符匹配,两个指针都向前移动。
- 如果不匹配,根据next数组调整子串的指针j,主文本的指针i不回溯。
示例
假设主文本是"ABABDABACDABABCABAB",子串是"ABABCABAB":
应用场景
KMP算法广泛应用于文本编辑器、搜索引擎、生物信息学中的DNA序列匹配等领域,特别是在需要高效处理大量文本数据的场景中。
如果你对具体实现或代码示例感兴趣,可以告诉我,我可以进一步解释。
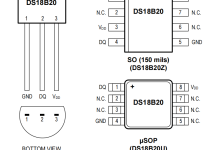
 网硕互联帮助中心
网硕互联帮助中心


评论前必须登录!
注册