目录
无监督学习
定义
聚类
简介
K-Means 算法
异常检测
简介
高斯正态分布
评估异常检测系统
异常检测 vs 监督学习
特征选择
主成分分析(PCA)
降维
关联规则学习
无监督学习
定义
在没有标准答案(标记)的情况下,从数据本身中发现内在的结构、模式和规律。
聚类
简介
-
目标:将数据分组,使得组内样本相似,组间样本不相似。
-
好比:你将一堆不同的水果混在一起,然后算法根据它们的形状、颜色、大小,自动分成“苹果堆”、“香蕉堆”、“橙子堆”。你事先并没有告诉算法“苹果”是什么。
-
关键术语:
-
样本/数据点:数据集中的每个个体(如每个客户、每篇文章)
-
特征/维度:描述样本的属性(如客户的年龄、收入)
-
簇/类:聚类后形成的分组
-
质心:一个簇的中心点(通常是该簇所有点的平均值)
-
-
经典算法:K-Means, DBSCAN, 层次聚类。
-
对比聚类(无监督)分类(有监督) 目标 发现数据的内在结构 学习特征与标签的映射关系 -
应用:
-
客户分群:根据购买行为将客户分成不同群体,进行精准营销。
-
社交网络分析:发现社区。
-
图像分割:将图片中相似的像素点聚成一类,从而区分出物体。
-
K-Means 算法
步骤
1.聚类的数量k需要预先指定
(一般情况下k越大代价函数就会越小,通过最小化代价函数来选择k就是让k最大,所以不合理)
1)肘部法则(Elbow Method)
- 尝试不同的k值(k=1,2,3,…)
- 对每个k,计算WCSS值
- 绘制k-WCSS曲线
- 寻找“肘点”——WCSS下降速度突然变缓的点
2)轮廓系数法
轮廓系数是衡量聚类质量的指标,衡量一个样本点与自己的聚类有多相似,与其他聚类有多不相似。通常通过比较不同 K 值下的轮廓系数,来找出最合适的 k 值
对于单个样本点 i:
a(i) = 点 i 到同簇其他点的平均距离(凝聚度)
b(i) = 点 i 到最近其他簇所有点的平均距离(分离度)
轮廓系数 s(i) = (b(i) – a(i)) / max(a(i), b(i))
3)根据聚类应用的业务来决定
2.初始化:随机选择 k 个点作为初始质心(聚类中心),(如果一个中心一开始没有分配到任何样本,那之后的结果都是0,没什么意义,所以刚开始就把它删掉或者重新初始化)
初始化位置不同会得到不同的结果,如
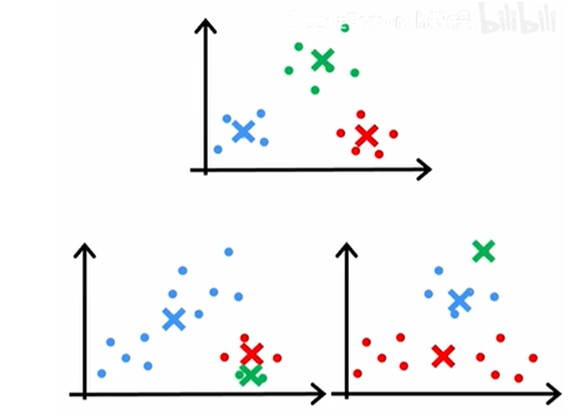
所以要进行多次初始化并运行得到不同的结果(50-100次),再选出代价函数最小的一个作为最 终结果(如上图,下边两个图的代价函数显然比第一个图大),以防止掉入局部最优陷阱。
3.分配:对每个数据点,计算到所有质心的距离,将其分配给最近的质心所在的簇
4.更新:重新计算每个簇的质心(取该簇所有点的平均值),更新质心的位置
5.重复步骤2-3,直到质心不再变化或达到最大迭代次数
优化目标
代价函数:失真函数
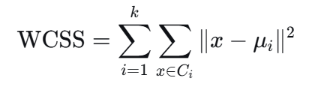
-
其中x表示样本点(也是样本点位置),Ci表示x所属的质心索引,μi表示质心Ci所在位置
-
WCSS:簇内平方和误差,意为所有样本点到其质心的距离平方之和
-
值越小,说明簇内点越集中,聚类效果越好
异常检测
简介
异常检测的任务是识别数据集中与大多数数据显著不同的样本。
异常点(离群点)的特点:
-
罕见性:出现频率低
-
差异性:与正常模式显著不同
-
影响性:可能表示重要信息(如欺诈、故障)
异常 vs 噪声
| 有意义的偏离模式 | 随机误差 |
| 可能包含重要信息 | 通常需要被过滤 |
| 是数据生成机制的一部分 | 测量或传输错误 |
高斯正态分布
单变量高斯:
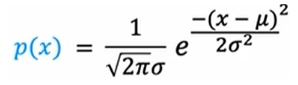
其中
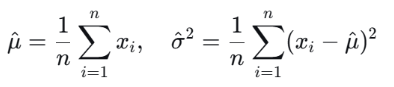
——————
多变量:
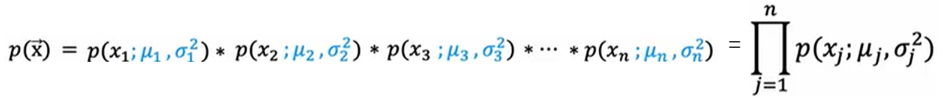
表示一个样本的概率等于它的所有的特征的概率的乘积
——————
1.选择n个特征
2.为训练集中的每种特征都分别拟合参数μ和σ^2,可向量化得到
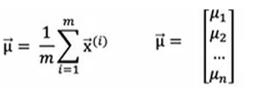
3.计算需要测试的样本的各个特征概率的乘积作为该样本的概率
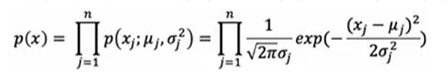
4.判断这个概率是否小于![]() ,来判断它是否异常
,来判断它是否异常
评估异常检测系统
将所有样本划分为训练集、交叉验证集和测试集,其中
-
训练集:大量的已知为正常的样本(不小心混入一两个异常样本也不影响最终的算法)
-
验证集:大部分的正常样本(人工赋予标签0)和少量的异常样本(人工赋予标签1)。
-
测试集:同验证集,人工赋予标签是为了知道对错,观察算法效果
在使用无标签训练集训练后,从带标签的验证集上评估并调整阈值或模型参数,最终在测试集上评估。
异常检测 vs 监督学习
| 标签需求 | 所有样本都要标签 | 通常只有正常样本标签,或完全无标签 |
| 数据分布 | 各类样本相对均衡 | 异常样本极少(<1%常见) |
| 异常类型 | 训练见过的异常类型 | 可能遇到全新类型的异常 |
异常检测是在正常样本上训练,学习正常数据的边界,将那些偏离正常的样本判为异常,所以即使是全新异常也能捕捉到。
而监督学习主要目的适用于分类,如果出现新异常是不能判别的。
特征选择
如果某个特征的分布并不近似于高斯分布,想办法做一些变换让它接近高斯分布,常用方法有对数变换(右偏/长尾分布),平方根变换(中度右偏)等
选择特征的标准:
正常数据中:特征值波动小(方差小) 异常数据中:特征值变化大
-
异常样本明显超出正常范围的特征
-
异常样本分布与正常明显不同的特征
高度相关(如相关系数>0.9)的特征只留一个,避免冗余特征
有时可以通过组合两个旧特征形成一个新特征来帮助异常检测识别,因为单个特征正常 ≠ 组合正常。
常用组合方法:
-
交互特征,新特征 = 特征A × 特征B
-
比值特征,新特征 = 特征A / (特征B + ε) ,ε防止除0
-
差值特征,新特征 = |特征A – 特征B|,衡量偏离程度
-
条件特征,
if 条件A成立 and 条件B成立:
新特征 = 1 # 异常模式
else:
新特征 = 0 # 正常模式
主成分分析(PCA)
从多个角度看数据,找到最重要的视角,用更少的维度描述数据
例如
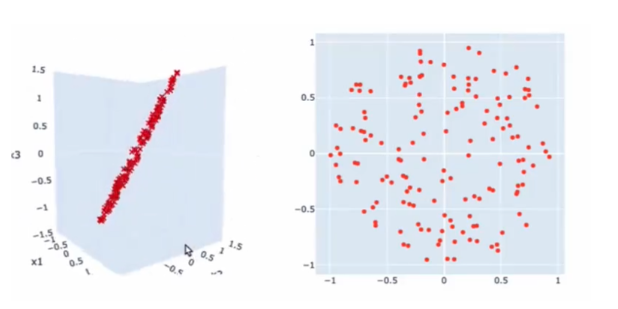
其原本是三维数据,但可以通过构建新的轴(主成分)z1,z2来使它降成二维可视化且不损失数据。
步骤
数据中心化,将特征归一化为零均值,并且如果不同特征的取值范围非常不同(1000米和2分钟),那还需要进行特征缩放
将数据投影到轴上时得到的方差最大的轴就是主成分,方差大就是点的投影比较分散,此时得到的信息比较多。
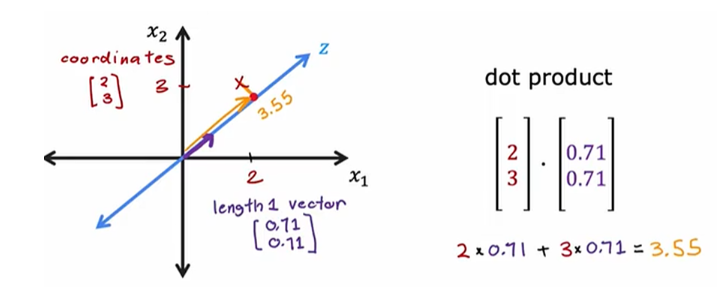
以这个为例,[2,3]是原来的坐标,[0.71,0.71]是主成分的方向向量,点积的结果就是该样本在新轴上的表示。
重构:知道PCA后的结果,反推原来的表示。比如上图那个,可以用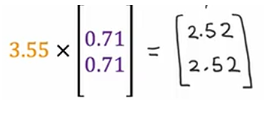
近似推回原来的。
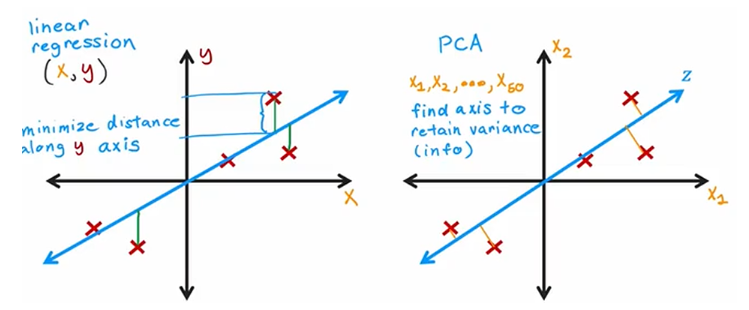
下图是线性回归与二合一PCA的区别,前者拟合函数使得预测值尽量接近真实y值(标签),衡量的是y轴方向(竖直方向);后者的两个轴是平等的,都是特征,没有标签,目的是让到主成分的垂直距离尽量小,这样在主成分那个方向上就会更分散,信息更多。
scikit-learn实现
# 导入所需库
import numpy as np
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
# 1. 加载数据(以鸢尾花数据集为例,可以替换为自己的数据集)
data = load_iris()
X = data.data # 特征数据,形状为(150, 4),即150个样本,4个特征
y = data.target # 标签(可选,用于可视化)
# 2. 数据标准化(特征缩放和中心化)
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X) # 标准化后,每个特征的均值为0,方差为1
# 3. 构建并训练PCA模型
# 方式1:指定保留的主成分数量(例如保留2个)
pca = PCA(n_components=2) # n_components可以是整数(指定数量)或浮点数(指定解释方差比例,如0.95表示保留95%方差)
X_pca = pca.fit_transform(X_scaled) # 拟合模型并对数据进行降维
# 方式2:指定解释方差比例(例如保留95%的方差)
# pca = PCA(n_components=0.95)
# X_pca = pca.fit_transform(X_scaled)
# 4. 分析PCA结果
print(f"原始数据形状:{X.shape}")
print(f"降维后数据形状:{X_pca.shape}")
print(f"各主成分的解释方差比例:{pca.explained_variance_ratio_}")
print(f"累计解释方差比例:{np.sum(pca.explained_variance_ratio_)}")
print(f"特征值(各主成分的方差):{pca.explained_variance_}")
# 5. 可视化降维后的数据(可选,仅当降维到2维时)
plt.figure(figsize=(8, 6))
for target, color, label in zip([0, 1, 2], ['r', 'g', 'b'], data.target_names):
plt.scatter(X_pca[y == target, 0], X_pca[y == target, 1], c=color, label=label)
plt.xlabel('第一主成分')
plt.ylabel('第二主成分')
plt.title('PCA降维后的鸢尾花数据')
plt.legend()
plt.show()
降维
-
目标:在尽可能保留信息的前提下,减少数据的特征数量。
-
好比:你有一份描述一个人的100个特征(身高、体重、发色、鞋码、星座…),但很多特征是冗余或不重要的。降维就是找出最重要的10个特征,仍然能很好地描述这个人。
-
经典算法:主成分分析(PCA), t-SNE, UMAP。
-
应用:
-
数据可视化:将高维数据降到2D或3D,便于我们人类观察和理解。
-
去除噪声和冗余:为后续的监督学习模型准备更干净、更有效的特征。
-
数据压缩。
-
关联规则学习
-
目标:发现数据中特征之间的关联关系。
-
经典算法:Apriori。
-
应用:
-
购物篮分析:经典的“啤酒和尿布”故事,发现顾客经常同时购买的商品,用于货架摆放或捆绑销售。
-
医疗诊断:发现某些症状和疾病之间的关联。
-
 网硕互联帮助中心
网硕互联帮助中心




评论前必须登录!
注册