P3819 松江 1843 路
题目描述
涞坊路是一条长
L
L
L 米的道路,道路上的坐标范围从
0
0
0 到
L
L
L,路上有
N
N
N 座房子,第
i
i
i 座房子建在坐标为
x
i
x_i
xi 的地方,其中住了
r
i
r_i
ri 人。
松江 1843 路公交车要在这条路上建一个公交站,市政府希望让最多的人得到方便,因此希望所有的每一个的居民,从家到车站的距离的总和最短。
公交站应该建在哪里呢?
输入格式
第一行输入
L
L
L、
N
N
N。
接下来
N
N
N 行,每行两个整数
x
i
x_i
xi 和
r
i
r_i
ri。
输出格式
一个整数,最小的每个人从家到车站的距离的总和。
输入输出样例 #1
输入 #1
100 3
20 3
50 2
70 1
输出 #1
110
输入输出样例 #2
输入 #2
100 2
0 1
100 10
输出 #2
100
输入输出样例 #3
输入 #3
10000000000 5
3282894320 391
4394338332 929
6932893249 181
7823822843 440
9322388365 623
输出 #3
5473201404068
说明/提示
样例解释 1
当建在坐标
40
40
40 的时候,所有人距离车站的距离总和为
∣
20
−
40
∣
×
3
+
∣
50
−
40
∣
×
2
+
∣
70
−
40
∣
×
1
=
110
|20-40| \\times 3+|50-40| \\times 2+|70-40| \\times 1=110
∣20−40∣×3+∣50−40∣×2+∣70−40∣×1=110。
数据范围和约定
对于 $10% $的数据,
1
≤
N
≤
50
1\\le N \\le 50
1≤N≤50,
R
i
=
1
R_i=1
Ri=1。
对于
30
%
30\\%
30% 的数据,
1
≤
N
≤
100
1 \\le N \\le 100
1≤N≤100,
R
i
≤
10
R_i \\le 10
Ri≤10,
1
≤
L
≤
1000
1 \\le L \\le 1000
1≤L≤1000。
对于
70
%
70\\%
70% 的数据,
1
≤
N
≤
1000
1 \\le N \\le 1000
1≤N≤1000,
R
i
≤
100
R_i \\le 100
Ri≤100,
1
≤
L
≤
10
6
1 \\le L \\le 10^6
1≤L≤106。
对于全部数据,
1
≤
L
≤
10
10
1 \\le L \\le 10^{10}
1≤L≤1010,
1
≤
N
≤
10
5
1 \\le N \\le 10^5
1≤N≤105,
0
≤
x
i
≤
L
0 \\le x_i \\le L
0≤xi≤L,
1
≤
r
i
≤
1000
1 \\le r_i \\le 1000
1≤ri≤1000。
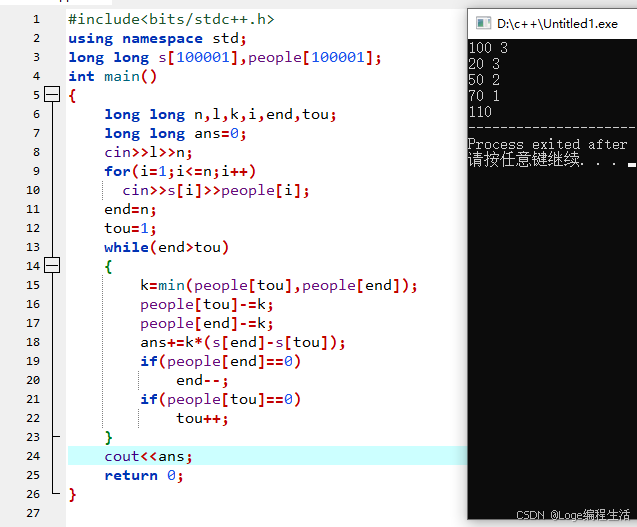
C++实现
#include<bits/stdc++.h>
using namespace std;
long long s[100001],people[100001];
int main()
{
long long n,l,k,i,end,tou;
long long ans=0;
cin>>l>>n;
for(i=1;i<=n;i++)
cin>>s[i]>>people[i];
end=n;
tou=1;
while(end>tou)
{
k=min(people[tou],people[end]);
people[tou]-=k;
people[end]-=k;
ans+=k*(s[end]–s[tou]);
if(people[end]==0)
end—;
if(people[tou]==0)
tou++;
}
cout<<ans;
return 0;
}
后续
接下来我会不断用C++来实现信奥比赛中的算法题、GESP考级编程题实现、白名单赛事考题实现,记录日常的编程生活、比赛心得,感兴趣的请关注,我后续将继续分享相关内容
 网硕互联帮助中心
网硕互联帮助中心



评论前必须登录!
注册