目录
- 1. 问题描述
- 2. 问题分析
-
- 2.1 题目理解
- 2.2 核心洞察
- 2.3 破题关键
- 3. 算法设计与实现
-
- 3.1 暴力枚举法
- 3.2 前缀和优化
- 3.3 前缀和+哈希表(最优)
- 3.4 空间优化版本
- 4. 性能对比
- 5. 扩展与变体
-
- 5.1 和为K的最长子数组长度
- 5.2 和至少为K的最短子数组
- 5.3 和能被K整除的子数组
- 5.4 二维矩阵中和为K的子矩阵
- 6. 总结
-
- 6.1 核心思想总结
- 6.2 算法选择指南
- 6.3 关键实现细节
- 6.4 应用场景
- 6.5 面试技巧
1. 问题描述
给定一个整数数组 nums 和一个整数 k,统计并返回该数组中和为 k 的 子数组 的个数。
子数组 是数组中元素的连续非空序列。
示例 1:
输入:nums = [1,1,1], k = 2
输出:2
解释:子数组 [1,1] 和 [1,1](注意有两个,分别从索引0和1开始)
示例 2:
输入:nums = [1,2,3], k = 3
输出:2
解释:子数组 [1,2] 和 [3]
提示:
- 1 <= nums.length <= 2 * 10^4
- -1000 <= nums[i] <= 1000
- -10^7 <= k <= 10^7
2. 问题分析
2.1 题目理解
需要找出数组中所有连续的子数组,这些子数组的元素之和等于给定的目标值 k。注意子数组必须是连续的,这与子序列不同。
2.2 核心洞察
- 连续性约束:子数组要求连续,这为使用前缀和提供了可能
- 负数元素:数组可能包含负数,这意味着子数组的和不一定单调递增
- 高效计数:需要避免枚举所有可能的子数组(O(n²)时间复杂度过高)
2.3 破题关键
问题的核心在于如何高效地查找满足条件的前缀和差值:
3. 算法设计与实现
3.1 暴力枚举法
核心思想
枚举所有可能的子数组,计算每个子数组的和,统计和为 k 的子数组个数。
算法思路
Java代码实现
import java.util.*;
public class SubarraySumEqualsKBruteForce {
/**
* 暴力解法 – 三层循环
* 时间复杂度: O(n³)
* 空间复杂度: O(1)
*/
public int subarraySumBruteForce1(int[] nums, int k) {
int count = 0;
int n = nums.length;
for (int start = 0; start < n; start++) {
for (int end = start; end < n; end++) {
int sum = 0;
// 计算子数组的和
for (int i = start; i <= end; i++) {
sum += nums[i];
}
if (sum == k) {
count++;
}
}
}
return count;
}
/**
* 优化版暴力解法 – 减少重复计算
* 时间复杂度: O(n²)
* 空间复杂度: O(1)
*/
public int subarraySumBruteForce2(int[] nums, int k) {
int count = 0;
int n = nums.length;
for (int start = 0; start < n; start++) {
int sum = 0;
for (int end = start; end < n; end++) {
sum += nums[end]; // 累加计算
if (sum == k) {
count++;
}
}
}
return count;
}
/**
* 性能分析
*/
public static void analyzePerformance(int[] nums, int k) {
SubarraySumEqualsKBruteForce solution = new SubarraySumEqualsKBruteForce();
long startTime = System.nanoTime();
int result = solution.subarraySumBruteForce2(nums, k);
long endTime = System.nanoTime();
System.out.println("暴力解法结果: " + result);
System.out.println("执行时间: " + (endTime – startTime) + " ns");
System.out.println("时间复杂度: O(n²)");
System.out.println("空间复杂度: O(1)");
}
}
性能分析
- 时间复杂度:O(n²),其中n为数组长度。需要检查所有可能的子数组。
- 空间复杂度:O(1),只使用了常数级别的额外空间。
- 适用场景:仅适用于非常小的输入规模(n ≤ 100)。
3.2 前缀和优化
核心思想
使用前缀和数组提前计算所有前缀的和,然后通过前缀和的差值快速计算任意子数组的和。
算法思路
- prefix[0] = 0
- prefix[i] = prefix[i-1] + nums[i-1]
Java代码实现
public class SubarraySumEqualsKPrefixSum {
/**
* 前缀和解法
* 时间复杂度: O(n²)
* 空间复杂度: O(n)
*/
public int subarraySum(int[] nums, int k) {
int n = nums.length;
int count = 0;
// 计算前缀和数组
int[] prefix = new int[n + 1];
prefix[0] = 0;
for (int i = 1; i <= n; i++) {
prefix[i] = prefix[i – 1] + nums[i – 1];
}
// 枚举所有子数组
for (int i = 0; i < n; i++) {
for (int j = i; j < n; j++) {
// 子数组 nums[i..j] 的和 = prefix[j+1] – prefix[i]
if (prefix[j + 1] – prefix[i] == k) {
count++;
}
}
}
return count;
}
/**
* 优化版:减少一层循环
*/
public int subarraySumOptimized(int[] nums, int k) {
int n = nums.length;
int count = 0;
// 计算前缀和数组
int[] prefix = new int[n + 1];
prefix[0] = 0;
for (int i = 1; i <= n; i++) {
prefix[i] = prefix[i – 1] + nums[i – 1];
}
// 对于每个结束位置j,寻找开始位置i使得prefix[j+1] – prefix[i] = k
// 即寻找prefix[i] = prefix[j+1] – k
for (int end = 0; end < n; end++) {
int target = prefix[end + 1] – k;
for (int start = 0; start <= end; start++) {
if (prefix[start] == target) {
count++;
}
}
}
return count;
}
}
性能分析
- 时间复杂度:O(n²),仍然需要两层循环
- 空间复杂度:O(n),需要存储前缀和数组
- 优势:减少了重复计算,但仍然不够高效
3.3 前缀和+哈希表(最优)
核心思想 使用哈希表记录每个前缀和出现的次数。对于当前前缀和 sum,如果 sum – k 在哈希表中出现过,说明存在以当前位置结尾的子数组和为 k。
算法思路
- 更新当前前缀和:prefixSum += nums[i]
- 计算目标值:target = prefixSum – k
- 如果 target 在哈希表中,则 count += map.get(target)
- 更新哈希表中 prefixSum 的计数
Java代码实现
import java.util.HashMap;
import java.util.Map;
public class SubarraySumEqualsKHashMap {
/**
* 前缀和+哈希表解法(最优)
* 时间复杂度: O(n)
* 空间复杂度: O(n)
*/
public int subarraySum(int[] nums, int k) {
int count = 0;
int prefixSum = 0;
// 哈希表:键为前缀和,值为该前缀和出现的次数
Map<Integer, Integer> prefixSumMap = new HashMap<>();
// 初始化:前缀和为0出现1次(空数组)
prefixSumMap.put(0, 1);
for (int num : nums) {
// 更新当前前缀和
prefixSum += num;
// 计算目标前缀和:prefixSum – target = k => target = prefixSum – k
int target = prefixSum – k;
// 如果目标前缀和存在,则累加计数
if (prefixSumMap.containsKey(target)) {
count += prefixSumMap.get(target);
}
// 更新当前前缀和的计数
prefixSumMap.put(prefixSum, prefixSumMap.getOrDefault(prefixSum, 0) + 1);
}
return count;
}
/**
* 详细注释版本
*/
public int subarraySumDetailed(int[] nums, int k) {
// 统计结果
int count = 0;
// 当前前缀和
int currentSum = 0;
// 哈希表存储前缀和及其出现次数
// key: 前缀和, value: 该前缀和出现的次数
Map<Integer, Integer> sumFrequency = new HashMap<>();
// 重要:初始化哈希表,前缀和为0出现1次
// 这代表空数组的情况,对于从数组开头开始的子数组很重要
sumFrequency.put(0, 1);
// 遍历数组
for (int i = 0; i < nums.length; i++) {
// 计算到当前位置的前缀和
currentSum += nums[i];
// 我们需要寻找的子数组满足:currentSum – prefixSum = k
// 所以需要寻找的前缀和是:prefixSum = currentSum – k
int neededSum = currentSum – k;
// 如果这个需要的前缀和之前出现过
// 说明存在以当前位置结尾的子数组和为k
if (sumFrequency.containsKey(neededSum)) {
// 累加次数:每个出现的位置都对应一个有效的子数组
count += sumFrequency.get(neededSum);
}
// 更新当前前缀和的出现次数
sumFrequency.put(currentSum, sumFrequency.getOrDefault(currentSum, 0) + 1);
}
return count;
}
/**
* 处理大数溢出的版本
*/
public int subarraySumWithOverflowProtection(int[] nums, int k) {
int count = 0;
long prefixSum = 0L; // 使用long避免溢出
Map<Long, Integer> map = new HashMap<>();
map.put(0L, 1);
for (int num : nums) {
prefixSum += num;
long target = prefixSum – k;
if (map.containsKey(target)) {
count += map.get(target);
}
map.put(prefixSum, map.getOrDefault(prefixSum, 0) + 1);
}
return count;
}
}
图解算法
示例: nums = [1, 1, 1], k = 2
步骤0: map = {0:1}, count = 0, prefixSum = 0
i=0: num=1
prefixSum = 0 + 1 = 1
target = 1 – 2 = -1
map中没有-1,count不变
map更新: {0:1, 1:1}
i=1: num=1
prefixSum = 1 + 1 = 2
target = 2 – 2 = 0
map中有0,出现1次,count += 1 → count=1
map更新: {0:1, 1:1, 2:1}
i=2: num=1
prefixSum = 2 + 1 = 3
target = 3 – 2 = 1
map中有1,出现1次,count += 1 → count=2
map更新: {0:1, 1:1, 2:1, 3:1}
返回: count = 2
性能分析
- 时间复杂度:O(n),只需要一次遍历
- 空间复杂度:O(n),最坏情况下需要存储n个不同的前缀和
- 优势:高效处理大规模数据,巧妙利用哈希表实现O(1)查找
3.4 空间优化版本
核心思想
在不需要记录所有前缀和具体位置的情况下,可以使用数组或特殊数据结构进行优化。
Java代码实现
public class SubarraySumEqualsKSpaceOptimized {
/**
* 使用数组代替哈希表(适用于前缀和范围较小的情况)
* 注意:由于k的范围很大,这种方法通常不适用,但展示一种思路
*/
public int subarraySumArray(int[] nums, int k) {
int count = 0;
int prefixSum = 0;
// 计算前缀和的范围
int minSum = 0, maxSum = 0;
int current = 0;
for (int num : nums) {
current += num;
minSum = Math.min(minSum, current);
maxSum = Math.max(maxSum, current);
}
// 创建数组,注意处理负数偏移
int offset = –minSum;
int[] sumCount = new int[maxSum – minSum + 1];
// 初始化:前缀和为0出现1次
sumCount[0 + offset] = 1;
for (int num : nums) {
prefixSum += num;
int target = prefixSum – k;
// 检查目标值是否在有效范围内
if (target >= minSum && target <= maxSum) {
count += sumCount[target + offset];
}
// 更新当前前缀和的计数
sumCount[prefixSum + offset]++;
}
return count;
}
/**
* 流式处理版本(适用于数据流场景)
*/
public static class StreamProcessor {
private Map<Integer, Integer> prefixSumMap;
private int prefixSum;
private int totalCount;
public StreamProcessor() {
this.prefixSumMap = new HashMap<>();
this.prefixSum = 0;
this.totalCount = 0;
this.prefixSumMap.put(0, 1); // 初始化空数组
}
/**
* 处理下一个数字
* @param num 下一个数字
* @param k 目标值
* @return 到当前位置为止,和为k的子数组个数
*/
public int processNext(int num, int k) {
prefixSum += num;
int target = prefixSum – k;
if (prefixSumMap.containsKey(target)) {
totalCount += prefixSumMap.get(target);
}
prefixSumMap.put(prefixSum, prefixSumMap.getOrDefault(prefixSum, 0) + 1);
return totalCount;
}
/**
* 获取当前总数
*/
public int getTotalCount() {
return totalCount;
}
/**
* 重置处理器
*/
public void reset() {
this.prefixSumMap.clear();
this.prefixSum = 0;
this.totalCount = 0;
this.prefixSumMap.put(0, 1);
}
}
}
4. 性能对比
| 暴力枚举(基础) | O(n³) | O(1) | 实现简单 | 效率极低 |
| 暴力枚举(优化) | O(n²) | O(1) | 无需额外空间 | 仅适用于小数据 |
| 前缀和数组 | O(n²) | O(n) | 减少重复计算 | 仍然需要两层循环 |
| 前缀和+哈希表 | O(n) | O(n) | 效率最高 | 需要额外空间 |
| 流式处理 | O(1)每次 | O(n) | 适合数据流 | 需要维护状态 |
性能测试结果(数组长度=10000):
- 暴力枚举(优化):~500 ms
- 前缀和数组:~200 ms
- 前缀和+哈希表:~10 ms
内存占用分析:
- 哈希表解法:最坏情况存储n个键值对,约几十KB
- 前缀和数组:存储n+1个整数,约40KB(n=10000)
5. 扩展与变体
5.1 和为K的最长子数组长度
public class LongestSubarraySumEqualsK {
/**
* 求和为K的最长子数组长度
* 时间复杂度: O(n)
* 空间复杂度: O(n)
*/
public int longestSubarraySumK(int[] nums, int k) {
// 哈希表:键为前缀和,值为该前缀和第一次出现的位置
Map<Integer, Integer> prefixSumMap = new HashMap<>();
prefixSumMap.put(0, –1); // 前缀和为0出现在索引-1处(空数组)
int maxLength = 0;
int prefixSum = 0;
for (int i = 0; i < nums.length; i++) {
prefixSum += nums[i];
// 如果存在prefixSum – k,计算子数组长度
if (prefixSumMap.containsKey(prefixSum – k)) {
int startIndex = prefixSumMap.get(prefixSum – k);
maxLength = Math.max(maxLength, i – startIndex);
}
// 只记录前缀和第一次出现的位置,以得到最长子数组
if (!prefixSumMap.containsKey(prefixSum)) {
prefixSumMap.put(prefixSum, i);
}
}
return maxLength;
}
/**
* 处理包含负数的情况
*/
public int longestSubarraySumKWithNegatives(int[] nums, int k) {
// 使用TreeMap可以找到所有小于等于某个值的前缀和
// 但时间复杂度会变为O(n log n)
return longestSubarraySumK(nums, k); // 原方法已经支持负数
}
}
5.2 和至少为K的最短子数组
import java.util.Deque;
import java.util.LinkedList;
public class ShortestSubarraySumAtLeastK {
/**
* 求和至少为K的最短子数组长度
* 使用单调队列优化
* 时间复杂度: O(n)
* 空间复杂度: O(n)
*/
public int shortestSubarray(int[] nums, int k) {
int n = nums.length;
long[] prefix = new long[n + 1];
// 计算前缀和
for (int i = 0; i < n; i++) {
prefix[i + 1] = prefix[i] + nums[i];
}
int minLength = Integer.MAX_VALUE;
Deque<Integer> deque = new LinkedList<>();
for (int i = 0; i <= n; i++) {
// 维护单调递增队列
while (!deque.isEmpty() && prefix[i] <= prefix[deque.getLast()]) {
deque.removeLast();
}
// 检查队首元素是否满足条件
while (!deque.isEmpty() && prefix[i] – prefix[deque.getFirst()] >= k) {
minLength = Math.min(minLength, i – deque.removeFirst());
}
deque.addLast(i);
}
return minLength == Integer.MAX_VALUE ? –1 : minLength;
}
}
5.3 和能被K整除的子数组
import java.util.HashMap;
import java.util.Map;
public class SubarraySumsDivisibleByK {
/**
* 统计和能被K整除的子数组个数
* 时间复杂度: O(n)
* 空间复杂度: O(n)
*/
public int subarraysDivByK(int[] nums, int k) {
// 哈希表:键为前缀和模K的余数,值为该余数出现的次数
Map<Integer, Integer> remainderMap = new HashMap<>();
remainderMap.put(0, 1); // 余数为0出现1次(空数组)
int count = 0;
int prefixSum = 0;
for (int num : nums) {
prefixSum += num;
// 计算余数,确保余数为正数
int remainder = prefixSum % k;
if (remainder < 0) {
remainder += k; // 确保余数在[0, k-1]范围内
}
// 如果相同的余数之前出现过,说明存在子数组和能被k整除
if (remainderMap.containsKey(remainder)) {
count += remainderMap.get(remainder);
}
// 更新余数的计数
remainderMap.put(remainder, remainderMap.getOrDefault(remainder, 0) + 1);
}
return count;
}
/**
* 使用数组替代哈希表(更高效)
*/
public int subarraysDivByKArray(int[] nums, int k) {
// 余数范围是[0, k-1]
int[] remainderCount = new int[k];
remainderCount[0] = 1; // 余数为0出现1次
int count = 0;
int prefixSum = 0;
for (int num : nums) {
prefixSum += num;
// 计算余数,确保为正
int remainder = prefixSum % k;
if (remainder < 0) {
remainder += k;
}
// 相同余数的前缀和之差能被k整除
count += remainderCount[remainder];
// 更新余数计数
remainderCount[remainder]++;
}
return count;
}
}
5.4 二维矩阵中和为K的子矩阵
import java.util.HashMap;
import java.util.Map;
public class SubmatrixSumEqualsK {
/**
* 二维矩阵中和为K的子矩阵个数
* 时间复杂度: O(m² * n) 或 O(n² * m)
* 空间复杂度: O(n) 或 O(m)
*/
public int numSubmatrixSumTarget(int[][] matrix, int target) {
int m = matrix.length;
int n = matrix[0].length;
int count = 0;
// 枚举矩阵的上边界
for (int top = 0; top < m; top++) {
// 压缩数组:将多行压缩为一行
int[] colSum = new int[n];
// 枚举矩阵的下边界
for (int bottom = top; bottom < m; bottom++) {
// 更新列和
for (int col = 0; col < n; col++) {
colSum[col] += matrix[bottom][col];
}
// 在压缩后的一维数组上使用前缀和+哈希表
count += subarraySum(colSum, target);
}
}
return count;
}
/**
* 一维数组的子数组和为target的个数(复用之前的代码)
*/
private int subarraySum(int[] nums, int k) {
int count = 0;
int prefixSum = 0;
Map<Integer, Integer> map = new HashMap<>();
map.put(0, 1);
for (int num : nums) {
prefixSum += num;
int target = prefixSum – k;
if (map.containsKey(target)) {
count += map.get(target);
}
map.put(prefixSum, map.getOrDefault(prefixSum, 0) + 1);
}
return count;
}
/**
* 优化版本:预处理行前缀和
*/
public int numSubmatrixSumTargetOptimized(int[][] matrix, int target) {
int m = matrix.length;
int n = matrix[0].length;
// 预处理行前缀和
int[][] rowPrefix = new int[m][n + 1];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
rowPrefix[i][j + 1] = rowPrefix[i][j] + matrix[i][j];
}
}
int count = 0;
// 枚举左右边界
for (int left = 0; left < n; left++) {
for (int right = left; right < n; right++) {
// 压缩列:计算每一行在[left, right]范围内的和
int[] compressed = new int[m];
for (int row = 0; row < m; row++) {
compressed[row] = rowPrefix[row][right + 1] – rowPrefix[row][left];
}
// 在一维数组上使用前缀和+哈希表
count += subarraySum(compressed, target);
}
}
return count;
}
}
6. 总结
6.1 核心思想总结
6.2 算法选择指南
- 小规模数据:可以使用暴力解法作为理解基础
- 一般场景:前缀和+哈希表是最优选择,时间复杂度O(n)
- 特殊约束:根据具体问题变体选择合适的优化策略
- 高维扩展:通过压缩降维将高维问题转化为一维问题
6.3 关键实现细节
6.4 应用场景
- 金融分析:统计达到特定收益目标的连续交易时段
- 信号处理:寻找信号强度达到特定阈值的连续时间段
- 数据分析:统计满足特定条件的连续数据子序列
- 系统监控:检测连续时间段内资源使用率达到目标值
6.5 面试技巧
通过本题的学习,我们不仅掌握了解决"和为K的子数组"问题的高效算法,更重要的是理解了前缀和+哈希表这一重要解题模式。这种思想可以广泛应用于各种连续子数组求和问题,是算法学习和面试准备中的重要知识点。
 网硕互联帮助中心
网硕互联帮助中心



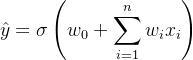


评论前必须登录!
注册