力扣每日一刷Day 8

Practice Day eight:Leetcode T1584

上一次，我们使用了Prim算法解决了最小生成树的问题，事实上Kruskal算法也是解决最小生成树的一个有效方法。我们可不能厚此薄彼，只讲解Prim算法而对Kruskal算法置之不理。

现在，我们先来讲解Kruskal算法的基本原理:

1 获取所有节点连成边的数值，如果数值为0，直接终止程序，输出结果。否则，进入下一步操作。

2 以从大到小，好吧，其实从小到大也行，总之，给他们排序

3 选取其中最小的边

4 判断这条边被实装后，是否会形成多个连通分量，用人话说，就是是否会成环

5 成环：那就滚蛋，我们要最小生成树，成环显然不符合我们的标准。

不成环：你过关。实装这条边。

6 判断此时所有节点是否已然被链接。若已然完全链接，终止程序。若未链接全部节点，则循环步骤3，4，5，6

完成对Kruskal算法的初步了解后，我们来看看题目要求：得到最小生成树。

没什么好说的，就用Kruksal算法。

但是题目这个图，比较有意思的是，他是以坐标的形式给出位置的，并不是直接把一个连通图的权重告诉你。

我想说的是，这样一来，我们的操作空间就变大了。为什么这么说？因为我们获得了一个新的信息：角度。

若是单纯给出一个无向链接图给你，你只能知道各个节点之间的权重，你只有这个信息。

但是以坐标形式给出，你就可以获知：节点之间的权重、权重间的夹角

来思考一下，这个夹角，他确实可以帮助我们简化代码吗？

更多时候，增加一个影响因素，他往往会让事情变得更复杂，这里也不列外。

但是，可以让我们的程序更加快速！哈哈哈哈！

来看看这是怎么一回事吧！

虽然Kruskal算法的核心是以边为基础展开的，所以，我们可以很轻易的知道，当边越多，越复杂的时候，算法实现时间会变得很长。对于这类图，我们管他叫稠密图。

对于稠密图，我们更喜欢用Prim算法进行解决。因为Prim算法是以点为基础的，边的多与寡，实际对算法的实现的时间影响并不大。

事实上，Kruskal更适合解决边更少的稀疏图，他在稀疏图上解决问题的时间远比Prim算法好得多。区分稠密图和稀疏图的临界条件，就是边的数目接近n^2/2。

这时你可能察觉出问题所在了：题目只给了坐标，左边两两相连可是有n（n-1）/2条边，这毫无疑问是稠密图，Kruskal算法完全不适用于这个题目。

没有Prim大人的力量，我们该如何战胜稠密图？！

作者淡然一笑，一把抓住稠密图，顷刻炼化！

我就是非得要用Kruskal，为什么非要算法适应题目？我完全可以改造题目，让他变得适应算法！

这时候就需要用到强大的几何武器了！

在一个平面三角形中：

古语有曰：大角对大边。

简而言之，就是角越大，边就越大。这个可以通过余弦定理严格证明。反正你高中学过了，对吧？

构成一个三角形，我们需要三个顶点，怎么排列都可以。

我们知道，若想连同三个点，实际上我们只需选择三条边中的其中两条即可。

若是需要最小生成树，则肯定不能选其中最大的这条边。

这样，我们就通过几何关系，减少了可以选择的边，稠密图，渐渐变成了稀疏图。

很明了了，我们可以通过【角度】来选择边。

怎么应用他？这好像很麻烦欸？夹角是相对而言的，也就是说，如果我要使用夹角这个信息，我不能孤立的使用它，我们必须有两条边才能使用他。

就算知道了边长，我们仍需通过三角形的余弦定理才能知道角度，md，这不是没事找事吗，我要知道长度了，还要什么角度。

所以角度的应用方式不是这样的，我们如果能找到一个特殊的角度，让他和边对应起来，那该有多好。边，实际上又是坐标的二级产物，而题目又是以坐标的形式给出，要求我们计算的是曼哈顿距离，而不是实际意义上的边长，那我们为什么不直接以曼哈顿距离的形式来等效处理这个边长呢？毕竟边长的大小实际上与曼哈顿距离（实际应描述为横向距离和纵向距离）是一 一对应的。

答案已经很明显了！聪明的你已经想到，这个角度，他就是45°，只有他，才可以很轻易的把横纵坐标给简单联系起来，因为这是一个可以通过数值简单二分类的模型，若横向距离与纵向距离相等，那就是45°，若不等，就不是45°，完全不需要进行别的处理。

先借力扣官方的图用一下

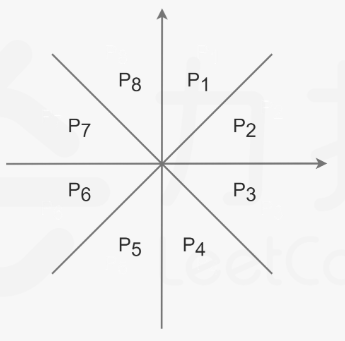
再结合我们前面的理论，我们可以得知，45°对应的角一定不会是最大角，也就是，这个角所对边一定不是最大边，这就强迫我们必须要在简单计算就知道了，不再过多描述。

可以看到，整个平面，被我们分为了八个部分。现在，我们就可以分区域进行处理了。

1 以选中的节点作为原点，实现这个非常简单，只需要把两个节点的坐标相减即可，这相当于平移坐标系，现在，我们管这个处于原点坐标叫做a

2 我们先以P1区为例，我们再随便取一个坐标，也许没这么幸运，一下就取到了P1区，我管他叫b

3 我们如何判定，b他确实在P1区间里面呢？再进一步，这个P1区到底是怎么划分的呢？我们知道，P1区不过是a点的引申，所以对于区域划分的问题，我们需要从a点入手。

4 我们知道，对于45°，其斜率为K=1，也就是说，对于恰好处于点a的45°方向的点（注意，这里描述的不是处于P1区域的点），应该满足Xz-Xa>0  这是为了保证b在a的右半区间         

Yz-Xz=Ya-Xa    这是因为处于a的P1区域的点，应该满足方程式Y-X=C(C是一个常数，表示对以原点出发的45°的校正数值，毕竟不管怎么说，我们的45°仍然以真正的原点及其坐标系为标准）

5 那么，很清晰了，若是点b处于P1区域，就应该满足Xb-Xa>0，以及Yb-Xb>C

6 在完成区域的判别之后，我们就需要进行最短边的判断。我们知道，对于处于P1区域的点而言，曼哈顿距离可以被表示为D=（Xz-Xa）+（Yz-Ya）=（Xz+Yz）-（Xa+Ya），有意思的是，Xa+Ya在此处实际上是个定值，在处理的过程中，会改变的只有Xz+Yz。也就是说：（Xz+Yz）越大，曼哈顿距离就越大

7 那么，对于曼哈顿距离的判断，就简化为了对所选节点（Xz+Yz）值的判断，这个值可不会因为参考系的改变而改变，减少了我们大量的存储工作与存储空间，并且这个是每一个节点独有的值

8 记录处于P1区域的所有值，通过二叉搜索树（BIT），选出其中的最小值，放入队列，保留他。

9 那么剩下的P2，P3，P4也是同样的操作，记录下本区间的最小值。为什么不把左侧也一起计算了，为什么只计算右侧？因为这样就会造成重复。来想一想吧！我们是需要对所有节点都进行这个操作的！这意味着什么？！

10 意味着，处于最左侧的节点一定会被选中！只要他被选中，就意味着除了他之外的节点就一定会与他产生联系，因为我们的计算流程就是这么设计的，由于这是一个无向图，描述为a与b连接，与描述为b与a连接，实际上地位是等价的，a的右侧，实际上就是b的左侧，只不过主体不同，描述方式不同而已：我的边，就是你的边

11 所以，我们只需要计算一侧，就足以计算所有节点之间的联系了，如果全方位进行计算，就会浪费计算资源，没有这个必要

12 一个节点，最多引申出八条边与其他节点连接，因为每个区域，只有一条最短边。这当然不是什么二级结论，这只是我们由区域划分而得出来的数字。

13 欸，有人可能会说：你怎么证明这八条边肯定能连接所有节点？其实你可以这样想：其实，这就是每个节点自发的找离自己最近的节点。虽然这有违Kruskal算法的思想，反而与Prim算法的思想更接近，但实际上，筛查的时候我们利用的是Kruskal算法，所以他是当之无愧的Kruskal算法。

13 我们完成了对边的减少后 ，这完全就是一个稀疏图了。把这些筛选后的边扔进队列中，然后为他们排序。

14 取出最小边，判断它是否成环，这一点，我们可以使用并查集来实现，只需要判断其是否属于同一个父节点就可以了。

15 成环：舍弃，选取下一条边长继续工作

 不成环：选取他，将其放入图中，然后记录边长

16 循环以上步骤14与步骤15。

17 当无边可选时，程序终止

流程已然大致梳理了一遍，下面，就是程序的构建了。

并查集（Disjoint-Set）

比较抱歉的是，我并没有在前几天的每日一练中发布有关并查集的内容，所以，在此处卡住的小伙伴们可以先去B站查询相关内容，几分钟就可以搞定。

简单来说，并查集就是查询每一个节点归属的一种树状结构。

学习了并查集后，我们来构建一个并查集，来帮助我们判断所选节点是否成环。

1 并查集有四个要素：节点个数、每个节点的秩（树的高度）、父节点、子节点

2 为了更快一些，也许我们的元素并不是只查询这么一次，我们希望后续的查询中能快一些。想想看吧，这个结构树是怎么构成的？比较坏的情况是一级一级向上查询，那我希望在这次一查询后，以后就不要这样这么慢的查询了，所以我直接把这一级节点挂到父节点上面，这样，我在下次查询后，只需要再向上查一级，我就知道本节点是从属于这个父节点。人们给这种操作取了一个动人的名字，路径压缩。

3 上面说的是已经连接好的情况，如果，是新连接的呢？这就意味着，合并。合并也是有讲究的，哪两个节点合并？以什么形式合并？

4 第一，合并通常是父节点之间进行合并，如果你想把一个节点合并到另一个节点上，请务必找到这两个节点的父节点，然后再合并父节点

5 第二，就合并的方式而言， 通常有两种，不过他们统称为“按秩合并”，第一种是按树高合并，也就是哪棵树更高，矮的那棵树的父节点就连接到高的那颗树的父节点上。不过这会产生一些幻觉。因为涉及到路径压缩的话，进行路径压缩后，树的实际高度可能会变矮，导致会出现两棵树等高，或者高一些的树合并到矮一些的树上面，不过无伤大雅，这个法子还是很好用的，并不会因为些许幻觉产生不稳定性。

6 为了解决这个幻觉，我们有第二种办法，按节点个数合并，谁节点更多，谁就做爸爸，因为儿子的个数不会因路径压缩而发生改变。

以下是代码实现：

class DisjointSetUnion {
private:
vector<int> f, rank;
int n;

public:
DisjointSetUnion(int _n) {
n = _n;
rank.resize(n, 1);
f.resize(n);
for (int i = 0; i < n; i++) {
f[i] = i;
}
}

int find(int j) {
return f[j] == j ? j : f[j] = find(f[j]);
}

int unionSet(int j, int k) {
int fj = find(j), fk = find(k);
if (fj == fk) {
return false;
}
if (rank[fj] < rank[fk]) {
swap(fj, fk);
}
rank[fj] += rank[fk];
f[fj] = fj;
return true;
}
};

其中，

find（）函数就是路径压缩，以迭代的方式完成。

unionSet（）函数就是检查是否成环，以及按秩合并。

接着，我们来构建二叉索引树（Binary Indexed Tree）的类，又名树状数组，没学过的小伙伴可以看看这个视频https://www.bilibili.com/video/BV1pE41197Qj/?spm_id_from=333.1387.homepage.video_card.click&vd_source=f8b81fa5a70ab21de75192e5c7ec720chttps://www.bilibili.com/video/BV1pE41197Qj/?spm_id_from=333.1387.homepage.video_card.click&vd_source=f8b81fa5a70ab21de75192e5c7ec720c

好吧，我承认有些操之过急。构建他的原因是：快速找到分隔的四块P1，2，3，4中，每个区域的最小边

1 首先，构成树状数组的要素有三个：

①用于记录数值的数组：这里是记录每个节点本身的特征值，这里的特征值是一个统称。先给这个数组命个名吧，既然他叫树状数组，那我们就管他叫tree。对于tree而言，实际上，它记录了两种信息。看看他的形态tree[pos]=val

我们发现，它可以在两个地方记录信息：数组索引pos，存储的值val。

这分别用于干什么呢？

对于数组索引pos，用来划定区域，也就是我们的P1，2，3，4

而存储的值val，则是用来判断最短边

我们仍旧用P1进行举例。

我们来看看pos是怎么来的，又是怎么运作，才拥有了划分区域的能力

回想以下划分区域的条件：Xb-Xa>0，以及Yb-Xb>C=Ya-Xa

首先，我们需要确保取到的点，好吧，其实我们需要取两个点。如何确保你在以其中一个点为基准点时，另一个点一定会在其右侧，也就是Xb-Xa>0？很简单，【排序】。只要按照X值的大小排序，我们先取X值最小的点作为基准点，那么即便另外一个点是随便取的，依然可以Xb-Xa>0。

对于排序，实现方法是构建一个可以同时存储x，y值的对象，你可能会想到每日一练8的键值对，但这里我们使用结构体更合适一些，因为我们还有别的信息需要存储，比如——索引。所以键值对是不合适的。

struct Pos {
int id, x, y;
}；

我们有诸多节点，显然一个结构体是不够的，所以我们需要一个存放结构体的容器。

vector<Pos> pos

有了这个，我们就可以进行排序的操作了

我们知道，C++的std::sort函数默认使用“<"运算符来比较两个元素的大小，对于自定义结构体Pos而言，当我们重载了运算符"<"后，sort就会调用这个重载版本来决定元素的排列顺序。

对于Pos而言，我们关注的是他的X值，因为我们要保证所选节点在基准节点右侧。但情况实际上还有另一种情况，也是唯一的一种情况：所选两点X值相同。这显然也需要一种排序方式，因为他是真实存在的情况，我们无法忽略他。所以，我们也要为他来涉及一个比较方式，简单起见，仍旧比较Ya<Yb即可。我们在结构体中补充一条运算符重载函数，以便sort函数可以调用他。

struct Pos {
int id, x, y;
bool operator<(const Pos& a) const { return x == a.x ? y < a.y : x < a.x; }
};

这里需要注意的是，三目运算符“  ？：”形成的是一个整体，并不是直接return x；而是通过大小的比较返回一个bool值。

然后进行排序

sort(pos.begin(), pos.end());

现在，数组pos以X值从小到大的形式排列好了。

完成了第一个条件的判定后，就需要进行第二个条件的判断，涉及到节点的特征值Yb-Xb

对于这样的计算，我们可以复用结构体Pos，计算每一个节点的特征值，对此，我们同样需要一个容器来存储这些计算的值。由于这是一个整数定值，我们把类型设为int

vector<int> a(n);

然后遍历vector<Pos> pos中的所有元素，将计算值记录到vector<int> a(n)中

for (int i = 0; i < n; i++) {
a[i] = pos[i].y – pos[i].x;
}

有时会出现一些节点Y-X相同的情况，这意味着这些节点都处于基准节点的同一个区域内，比如都处于基准元素的P1区域内。

这个现象除了告诉我们他们处于同一个区域，还告诉我们他会让程序检索时间变长，这是我们不愿看到的，比较好的办法是让每一个特征值Y-X变得独特，成为索引一样的存在，但我们又不希望改变数组a，因为数组a的索引代表他是不同节点产生的特征值。

所以我们另设一个数组b，专门用于存放没有重复的特征值Y-X，让其成为分界线一样的存在，通过检索b的索引，我们就能知道坐标处于哪一个区域。由于我们不知道重复值的个数，先暂且设容器大小为n

vector<int> b(n)；

当然，合理起见，我们应该与a一同处理，也就是在上一条程序的for循环加上数组b的处理

for (int i = 0; i < n; i++) {
a[i] = pos[i].y – pos[i].x;
b[i] = pos[i].y – pos[i].x;
}

然后，对数组b进行上述操作，让每个特征值独立，并使之可以成为被合理检索的存在。

为了可以轻易检索他，我们先把数组b进行排序，这样，我们就可以通过下标的形式进行区域划分。同时，这也是为了适配去重时erase函数的使用，因为erase函数只能删去特定区域的数字。

sort(b.begin(), b.end());

然后进行去重。

b.erase(unique(b.begin(), b.end()), b.end());

首先是利用unique函数把数组b所有重复的元素移到队列末尾，然后返回一个指向第一个重复元素的迭代器。之后，erase函数大手发力，抹除两个迭代器之间的重复元素。现在，数组b有了一个好听的名字——【映射表】。当然，你喜欢管他叫，【字典】，也是可以被接受的。

说了这么多，不要忘记初心，我们是要解释pos这个数组tree的索引是怎么来的

为了把索引名称和数组名pos区分，我们把计算用的索引名称叫poss

int poss = lower_bound(b.begin(), b.end(), a[i]) – b.begin() + 1;

通过lower_bound函数，他会返回一个在数组b中与数组a数值相等时的迭代器，当然，我们需要把他处理为数组索引，迭代器当然不能成为索引。但数组b是一个vector数组，他的内容是连续存储的，那么迭代器之间相减，得到一个差值，这就是数组b此时的索引了。但这还不够，因为二叉索引树的标号是从【1】开始的，而数组b是从【0】开始的，不进行标号对齐的话，会出现

lowbit（0）无意义的问题，所以，我们需要为数组b的索引

                                   lower_bound(b.begin(), b.end(), a[i]) – b.begin() 

进行加1的处理，以便对齐二叉索引树的标号。

这就是pos的来源了，如何使用它，我们后面会继续讲解

接下来讲解的是数组tree中存储的val，这又是怎么来的

文章有些太长了，我们重温一下上面的内容

在完成区域的判别之后，我们就需要进行最短边的判断。我们知道，对于处于P1区域的点而言，曼哈顿距离可以被表示为D=（Xz-Xa）+（Yz-Ya）=（Xz+Yz）-（Xa+Ya），有意思的是，Xa+Ya在此处实际上是个定值，在处理的过程中，会改变的只有Xz+Yz。也就是说：（Xz+Yz）越大，曼哈顿距离就越大

pos这个索引，事实上就完成了区块的划分，所以，tree存储的值应该是处于P1区块的节点的曼哈顿距离的魔改值（Xz+Yz），对于这个值的使用，我们后面会进行讲解

②用于记录索引的数组：通过相同的编号来记录索引。事实上，这个数组有两个索引，我们需要分清楚一些。我们设这个数组为idRec。对于这个idRec，进行查找时，有idRec[pos] = id。其中pos的来源，在①中已经解释过。现在，我们来解释“id”存储了什么值。

id，就是当前数组tree所使用的poss索引，在数组pos中的编号

                               pos[i]——>a[i]——>b[?]——>poss——>tree[poss]

也就是说，id=i，保留这个信息，是为了之后得胜最小边时，计算曼哈顿距离的依据

③构造BIT实例花费的数组大小：我们把这个传入的东西叫做n。

对于n，应该与数组tree含有的元素个数一致，这样，才能精确构建数组tree的大小，避免不必要的浪费，也是为了防止存储空间不足而越界。所以有

int num = b.size();

这里的num与n不是一个东西，由于构建的数组往往从0开始，所以实际上数组tree和数组idRec都要比实际存储元素总量大一位，以符合二叉索引树的应用规则，[0]号数组不存储东西，只是用来加塞。也就是说，n=num+1

对于num而言，这个值越大，说明P1区域划分的越精细，但同时也意味着搜索效率的降低。

拥有所有构建二叉索引树的要素之后，我们就开始构建二叉索引树

BIT(int _n) {
n = _n;
tree.resize(n, INT_MAX);
idRec.resize(n, -1);
}

我们在初始化时，应该把数组tree的每一个元素设置为最大，给予一个初始的比较值，因为我们的tree总是存储最小的（Xz+Yz），所以初始值，我们要设为无穷大，虽然无法在计算机实现无穷大，不过我们可以用int整形可以表达的最大值来表示无穷。

对于数组idRec而言，为什么要把初始元素设置为-1，这并没有什么特殊的，只是因为正数和零都需要被使用为编号索引，所以我们只能在负数中随机选择一个数，表示此时尚未存在该区域的tree被关联。

 此时二叉索引树初始化完成，接下来，我们来实现二叉索引树的功能。

哈哈，首先，是二叉索引树最关键的搜查组件，lowbit（）

int lowbit(int k) { return k & (-k); }

位与运算符&首先会把十进制的k转化为二进制，然后-k变成k取补码，也就是k按位取反，然后加一。接着&运算符就会比对k与-k之间的数字，若同一位次都是1，则取1，否则取0。这样，我们就可以得到二进制的k最右侧的1了。

这样设计的目的是什么？

来看看树状数组的形状，这里，我们借用一下B站up主鹤翔万里的图，以下是链接

https://www.bilibili.com/video/BV1pE41197Qj/?spm_id_from=333.1007.top_right_bar_window_history.content.click&vd_source=f8b81fa5a70ab21de75192e5c7ec720chttps://www.bilibili.com/video/BV1pE41197Qj/?spm_id_from=333.1007.top_right_bar_window_history.content.click&vd_source=f8b81fa5a70ab21de75192e5c7ec720c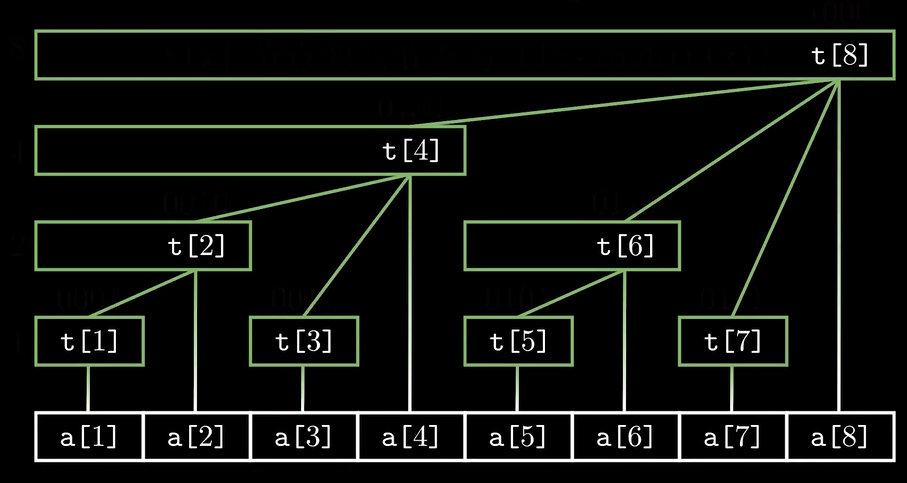

对于最底下的白色数组而言(注意这里的数组a不是我们编写的，只是图片的一个范例），他记录的是我们处理过后的数组b[  ]，也就是在P1区域某个范围内的最小值。现在，我们希望在之后可以更加快速的检索由数组b生成的poss对应的最小值，所以，我们构建了另外一个数组 t [ ]来存放某一区间（这里的区间指的是由poss生成的索引区间，因为poss的生成是有序的，所以区间也是有序的）内的最小值，在我们的代码里，数组tree[  ]等效于上面的数组 t [  ]。

我们来举例理解他吧：t[2]存储的是a[1]~a[2]里比较小的那个值，t[4]存储的是a[1]~a[4]中最小的那个值，t[8]存储的是a[1]~a[8]里最小的那个值。

这种可以通过父区间快速查找我们设定的规则（本题是最小值，当然，你可以自己DIY存储各种数据的树状数组）的树状结构，就是我们的树状数组了。

也就是说，只要查询对应的父节点，就可以获悉其管理的子节点的核心信息。在查询之前，树状数组是已经经过一次比对，才被被构建出来的，树状数组实质上只是为了方便后续查询的结构。

树状数组的核心思想是用父节点管理若干子节点的信息，而 lowbit 就是用来确定父节点与子节点的管辖关系的关键。

①lowbit可以帮助我们获得数组  t [  ]目前管理的元素个数，以及计算被管理元素的索引

例如：

• lowbit(8) = 8 → t[8] 管理 a[1]~a[8]（长度 8）
• lowbit(4) = 4 → t[4] 管理 a[1]~a[4]（长度 4）
• lowbit(6) = 2 → t[6] 管理 a[5]~a[6]（长度 2）
• lowbit(3) = 1 → t[3] 管理 a[3]（长度 1）

②lowbit可以作为步长进行迁越，找到父节点，或子节点

• 子节点 → 父节点：子节点的下标 i 加上 lowbit(i)，会跳转到父节点（管理更大区间）。
• 父节点 → 子节点：父节点的下标 i 减去 lowbit(i)，会跳转到子节点（管理更小、更细分的区间）。

• 示例：修改 a[3]（二进制 0011）

• lowbit(3) = 1（二进制 0001），因此：
  • 第一步：更新 t[3]（管理 a[3]）→ i = 3
  • 第二步：i += lowbit(3) → 3 + 1 = 4 → 更新 t[4]（管理 a[1]~a[4]，包含 a[3]）
  • 第三步：i += lowbit(4) → 4 + 4 = 8 → 更新 t[8]（管理 a[1]~a[8]，包含 a[3]）
  • 第四步：i += lowbit(8) → 8 + 8 = 16（超出数组长度 n=8，停止）

现在，理解了基本原理后，我们来构建update组件，与query组件混合使用。

update用于为树状数组tree插入数据，也就是上面树状数组的图片中的数组 t [  ]。

①tree是数组b的映射，以 int poss = lower_bound(b.begin(), b.end(), a[i]) – b.begin() + 1;的方式

②但我们仍需从数组a下手，因为数组a的索引与数组pos的索引是一一对应的，数组tree只是存储中间量的工具，我们仍然得通过准确的节点pos[i]来计算曼哈顿距离。

③tree存储的值val是特征值X+Y，也就是我们需要传入pos节点本身的x，y信息

这样一来，update就需要传入三个数据：poss、i、对应的真实节点pos[i].x与pos[i].y的信息

他的原型设置为

void update(int poss, int val, int id)

反正要记录特征值，一不做二不休，直接在传入参数的时候就计算

update(poss, pos[i].x + pos[i].y, i)

然后开始构建内部逻辑

由于一开始，tree所有元素被初始化为无穷大，所以，当我们按pos[i]插入时，他一定是整个数组tree中最小的值，则数组必然会更新。

在往后的操作中，也是需要比对数值，如果新插入的数值比原来的大，就不管他，跳过，不更新，如果插入的数值更小，就按步长往下走，更新沿途所有节点的值，直到节点小于0。

往下走的原因是，我们希望可以这么设计。因为这样可以节省更新节点的时间。可以得知，数组tree最后一个元素，必然是整个数组最小的元素，这一点，可以由上面的树状数组图很轻易的获知。

所以假设我们从X值大到小，也就是从最末尾的编号开始更新，他就会从父节点开始更新，不需要遍历所有子节点。在后续的流程中也是一样的道理。这样一来，遍历修改值的次数明显比从X值从小到大的次数要小，节省了不少时间。

那么，我们的步长就设置为自减，而不是我们常用的自增。

然后记录我们当前最小值的节点poss身份证编号i,存储到idRec，接着poss向下遍历，直至poss<=0,退出循环，因为我们的编号是从1开始的。

void update(int poss, int val, int id) {
while (pos > 0) {
if (tree[poss] > val) {
tree[poss] = val;
idRec[poss] = id;
}
poss -= lowbit(poss);
}

由于最顶层的数组一定是最小值，我们也只关心最小值，往下是如何实现的，其实我们并不需要对其过多关注

现在，我们需要另一个组件query用于查询特定区域最小的数值。因为update只提供插入功能，没有提供查询功能。

对于查询功能，我们需要传入当前poss值，找到当前区域最小的边长。值得一提的是，树状数组中的元素并不会最终都链接到同一个父结点上，一个树状数组最终可以有多个父节点。

幸运的是，我们可以通过poss这个索引可以通过自增作为桥梁，来跨进不同父节点所属的树，进行最小值查询。这时候，就符合二叉索引树的逻辑，自下向上，自左往右的搜索不同的树，利用lowbit步长跨越的功能，我们也能很快的检索到树状数组中的最小值。

既然是检索最小值，那么我们就应该存在返回最小值的功能，不过由于我们存储的是特征值val，到时我们要判断是否成环还要用到每个节点自身的独立性，否则，我们就可以直接使用tree存储的值来计算曼哈顿距离。所以此处，我们返回原始节点的索引。

这里涉及到一个问题，就是最小值能否是由不同的点计算出相同的答案？答案是不可能。因为进入树的节点都是经过Y-X的筛选的，不可能在Y-X比基准节点小的情况下，Y+X的值与基准节点计算的相同。

然后我们就需要考虑检索不到值的情况了。对于检索不到值的情况，我们也应有返回值，为了与节点编号有所区分，我们把无返回值设为-1。

为了可以找到最小值，且存在比对的对象，我们设用于比较的值minval初始时是无穷大。

int query(int pos) {
int minval = INT_MAX;
int j = -1;
while (pos < n) {
if (minval > tree[pos]) {
minval = tree[pos];
j = idRec[pos];
}
pos += lowbit(pos);
}
return j;
}

现在，我们已经完成了对二叉索引树的全部构建，来一张全家福吧。

class BIT {
public:
vector<int> tree, idRec;
int n;

BIT(int _n) {
n = _n;
tree.resize(n, INT_MAX);
idRec.resize(n, -1);
}

int lowbit(int k) { return k & (-k); }

void update(int pos, int val, int id) {
while (pos > 0) {
if (tree[pos] > val) {
tree[pos] = val;
idRec[pos] = id;
}
pos -= lowbit(pos);
}
}

int query(int pos) {
int minval = INT_MAX;
int j = -1;
while (pos < n) {
if (minval > tree[pos]) {
minval = tree[pos];
j = idRec[pos];
}
pos += lowbit(pos);
}
return j;
}
};

二叉索引树只是完成了对区域最小边的选择，我们需要一个另外一个组件，来利用二叉索引树构建边。

是的，到这里笔者已经写了12000字的思路了 ，才刚到边的构建。哈哈，不过寥寥一百多行的代码，居然有这么多门道。庞杂的思路被浓缩成精简的代码，真是让人着迷。

为了编写构造边的组件，我们需要另设一个函数，就管他叫build吧。

在进行build之前，我们需要知道保留的边的信息：

第一：构建他最主要的目的是知道边的长度

第二：我们不希望它成环，所以我们希望记录边的同时，可以同步记录构成它的两个节点的编号

第三：我们知道，后面会有容器存储边的信息，而且需要选取最小值。但存储了这么多信息的个体，需要一个主导元素来供给比较，这个主导元素就是曼哈顿长度。

基于上述要求，构建结构体是一个不错的选择，接着，为了满足比较的需求，我们需要重载运算符来供给后面的排序需要。

struct Edge {
int len, i, j;
Edge(int len, int i, int j) : len(len), i(i), j(j) {
}
bool operator<(const Edge& a) const {
return len < a.len;
}
};

这里需要注意的是，重载运算符前后都有一个const。

前面的const，是为了保证传入的参数不被修改

后面的const，是为了保证this指针所指的对象参数不被修改

既然完成了对边的构建，我们就需要有一个容器来存储生成的边

vector<Edge> edges;

对于build，既然它是构建边的函数，那他就应该包括我们构建二叉搜索树的所有操作，因为这本就是为他服务的。

我们整理一下思路吧：

①对所有节点pos按照X值由小到大排序

②设立两个数组a与b

③对b进行去重

④以b的大小为BIT构建实例

⑤进入循环，由编号从大到小为BIT更新最小值

⑥使用query搜查最小值

⑦若是搜查到最小值就计算曼哈顿距离，将其塞入数组edges中，供给Kruskal算法备选

⑧无论是否存在最小边，都以当前循环的编号使用update塞入新节点进BIT

⑨进入下一轮循环，重复⑤~⑧，直至所有元素被处理完成。

这里我们总是只考虑区域P1，所以这个函数应该还被别的函数所使用，这里我们只传入参数n来让下述操作正确构造数组即可，其他参数由调用build的函数来提供。

为什么要这么做？

因为在build函数中无论什么情况，都只有n，以及每个节点的pos[i].x与pos[i].y是不变的，且n是一个参数，不会影响程序运行速度。但若是每次n都传入pos的话，麻烦就大了。因为pos实际上是我们对传入的vector<vector<int>>& points的一种改造，如果每次使用pos，都要传入一次points数组进行赋值的话，程序就会变的奇慢无比。所以我们希望只对pos赋值一次就够了，后面就可以尽情的使用它，而不是每调用一次build就构造一次pos。

void build(int n) {
sort(pos.begin(), pos.end());
vector<int> a(n), b(n);
for (int i = 0; i < n; i++) {
a[i] = pos[i].y – pos[i].x;
b[i] = pos[i].y – pos[i].x;
}
sort(b.begin(), b.end());
b.erase(unique(b.begin(), b.end()), b.end());
int num = b.size();
BIT bit(num + 1);
for (int i = n – 1; i >= 0; i–) {
int poss = lower_bound(b.begin(), b.end(), a[i]) – b.begin() + 1;
int j = bit.query(poss);
if (j != -1) {
int dis = abs(pos[i].x – pos[j].x) + abs(pos[i].y – pos[j].y);
edges.emplace_back(dis, pos[i].id, pos[j].id);
}
bit.update(poss, pos[i].x + pos[i].y, i);
}
}

 需要注意的是，曼哈顿距离是一个绝对值，所以需要用到abs（）函数取绝对值

接下来，就只剩下最后一个组件了

由于我们以上操作，都默认是在P1区域进行的，而我们需要生成P1，P2，P3，P4四个区域的边，显然，我们需要一个函数来为我们达成这个目的，使之复用上面的build函数来完成四个区域所有边的生成，就叫它MST吧

我们以上操作，都是基于题目传入的数组和节点个数实现的。为了达成边生成的目的，这些信息也必不可少，所以除了传入的points数组之外，我们需要获取数组个数的参数

void MST(vector<vector<int>>& points, int n)

他没有返回值，因为他只是调用build函数生成边而已

首先，我们需要为build函数提供它需要的pos节点信息

pos.resize(n);
for (int i = 0; i < n; i++) {
pos[i].x = points[i][0];
pos[i].y = points[i][1];
pos[i].id = i;
}

构造对pos数组进行重构，使之大小为n，然后利用传入的二维数组赋值，将其表示为x，y，并赋予这些节点独特编号，以便我们使用并查集时可以探查是否成环，以及使用BIT时有检索的目标。

然后依次构建P1，P2，P3，P4区域的边

P1：直接调用build函数即可，因为我们默认就是设定P1为示例区域

build(n);

P2：既然build的默认处理方式是P1，那我们就把P2也化成P1区域的模样就好了，我们只需要对坐标进行一些变化，比如说：翻转

现在，X与Y都是正数，且P1区域是黏在Y轴上的，而P2是黏在X轴上的，且条件也是X与Y都是正数。

聪明的你已经想到了，我只需要交换X与Y的地位，就可以令P2区域像P1区域一样处理了

for (int i = 0; i < n; i++) {
swap(pos[i].x, pos[i].y);
}
build(n);

P3：我们知道，P3与P2在原来的坐标轴中是以X轴对称的，现在X与Y数值交换

本来应该是旋转X轴的操作，现在应该变成旋转Y轴，此时Y轴由pos[i].x表示，旋转它，即让其变为负的

for (int i = 0; i < n; i++) {
pos[i].x = -pos[i].x;
}
build(n);

P4：由于现在P3等效于P1，那么P4就等效为P2.想想以P1为基准时，对P2怎么操作的吧：交换X和Y的值。那么现在我们也要对P4进行同等操作，让他变成P1的形状。

build(n);
for (int i = 0; i < n; i++) {
swap(pos[i].x, pos[i].y);
}
build(n);

以下是完整的MST函数实现

void MST(vector<vector<int>>& points, int n) {
pos.resize(n);
for (int i = 0; i < n; i++) {
pos[i].x = points[i][0];
pos[i].y = points[i][1];
pos[i].id = i;
}
build(n);
for (int i = 0; i < n; i++) {
swap(pos[i].x, pos[i].y);
}
build(n);
for (int i = 0; i < n; i++) {
pos[i].x = -pos[i].x;
}
build(n);
for (int i = 0; i < n; i++) {
swap(pos[i].x, pos[i].y);
}
build(n);
}

我已经什么都不缺了

来构建题目的调用函数吧，他已经给了基本格式了

int minCostConnectPoints(vector<vector<int>>& points)

现在，我们需要按流程调用我们上面所有的组件

①获取元素个数n，这应该在调用函数之外进行，因为所有函数都用到了它，他必须是个全局变量

②生成所有可用的边，调用MST函数

③初始化并查集，调用DisjointSetUnion类的构造函数

④我们需要一个返回值，初始成本ret为0，然后一个用于计数的实例num，用于记录此时插入的节点个数，方便后续判断是否所有节点已经插入，然后可以终止程序。注意，num被初始化为1，因为每选用一条边，意味着纳入一个节点。虽然有时候选取的边链接的节点并不处于我们之前的父节点里面，形成两棵树，但它最后总是会成为一个整体的，所以初始为1是很合理的。

⑤把MST函数所有生成的边从小到大排序

⑥遍历整个edges，即存储最小边的数组

⑦利用并查集判断其是否成环，成环，并查集返回false，进行下一次循环

⑧不成环，累加当前边的长度ret，num计数加一

⑨判断num是否等于n，即是否所有点都已经加入，若是，终止程序，返回成本ret

⑩若所有节点仍未加入树中，循环⑥~⑨，直至程序终止，返回成本ret

这就是所有了

写的最长的一次，前面所有文章的字数加起来翻一倍都没有这一篇长。

最后，附上力扣官方的完整题解

作者：力扣官方题解

链接：https://leetcode.cn/problems/min-cost-to-connect-all-points/solutions/565801/lian-jie-suo-you-dian-de-zui-xiao-fei-yo-kcx7/

来源：力扣（LeetCode）

著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

class DisjointSetUnion {
private:
vector<int> f, rank;
int n;

public:
DisjointSetUnion(int _n) {
n = _n;
rank.resize(n, 1);
f.resize(n);
for (int i = 0; i < n; i++) {
f[i] = i;
}
}

int find(int x) {
return f[x] == x ? x : f[x] = find(f[x]);
}

int unionSet(int x, int y) {
int fx = find(x), fy = find(y);
if (fx == fy) {
return false;
}
if (rank[fx] < rank[fy]) {
swap(fx, fy);
}
rank[fx] += rank[fy];
f[fy] = fx;
return true;
}
};

class BIT {
public:
vector<int> tree, idRec;
int n;

BIT(int _n) {
n = _n;
tree.resize(n, INT_MAX);
idRec.resize(n, -1);
}

int lowbit(int k) {
return k & (-k);
}

void update(int pos, int val, int id) {
while (pos > 0) {
if (tree[pos] > val) {
tree[pos] = val;
idRec[pos] = id;
}
pos -= lowbit(pos);
}
}

int query(int pos) {
int minval = INT_MAX;
int j = -1;
while (pos < n) {
if (minval > tree[pos]) {
minval = tree[pos];
j = idRec[pos];
}
pos += lowbit(pos);
}
return j;
}
};

struct Edge {
int len, x, y;
Edge(int len, int x, int y) : len(len), x(x), y(y) {
}
bool operator<(const Edge& a) const {
return len < a.len;
}
};

struct Pos {
int id, x, y;
bool operator<(const Pos& a) const {
return x == a.x ? y < a.y : x < a.x;
}
};

class Solution {
public:
vector<Edge> edges;
vector<Pos> pos;

void build(int n) {
sort(pos.begin(), pos.end());
vector<int> a(n), b(n);
for (int i = 0; i < n; i++) {
a[i] = pos[i].y – pos[i].x;
b[i] = pos[i].y – pos[i].x;
}
sort(b.begin(), b.end());
b.erase(unique(b.begin(), b.end()), b.end());
int num = b.size();
BIT bit(num + 1);
for (int i = n – 1; i >= 0; i–) {
int poss = lower_bound(b.begin(), b.end(), a[i]) – b.begin() + 1;
int j = bit.query(poss);
if (j != -1) {
int dis = abs(pos[i].x – pos[j].x) + abs(pos[i].y – pos[j].y);
edges.emplace_back(dis, pos[i].id, pos[j].id);
}
bit.update(poss, pos[i].x + pos[i].y, i);
}
}

void solve(vector<vector<int>>& points, int n) {
pos.resize(n);
for (int i = 0; i < n; i++) {
pos[i].x = points[i][0];
pos[i].y = points[i][1];
pos[i].id = i;
}
build(n);
for (int i = 0; i < n; i++) {
swap(pos[i].x, pos[i].y);
}
build(n);
for (int i = 0; i < n; i++) {
pos[i].x = -pos[i].x;
}
build(n);
for (int i = 0; i < n; i++) {
swap(pos[i].x, pos[i].y);
}
build(n);
}

int minCostConnectPoints(vector<vector<int>>& points) {
int n = points.size();
solve(points, n);

DisjointSetUnion dsu(n);
sort(edges.begin(), edges.end());
int ret = 0, num = 1;
for (auto& [len, x, y] : edges) {
if (dsu.unionSet(x, y)) {
ret += len;
num++;
if (num == n) {
break;
}
}
}
return ret;
}
};

感谢各位阅读到此处，我们不日相见。