一文全面入门强化学习：从基础概念、策略梯度、REINFORCE、RLOO、TRPO到PPO、GRPO算法

前言

本文对RL入门做一个串联，中间会穿插着各种关键结论和优化以及对应的细节文章，细节可以去对应的文章观看。

从RL基础理论 -> 策略梯度 -> REINFORCE -> RLOO/TRPO -> PPO -> GRPO

RL理论基础

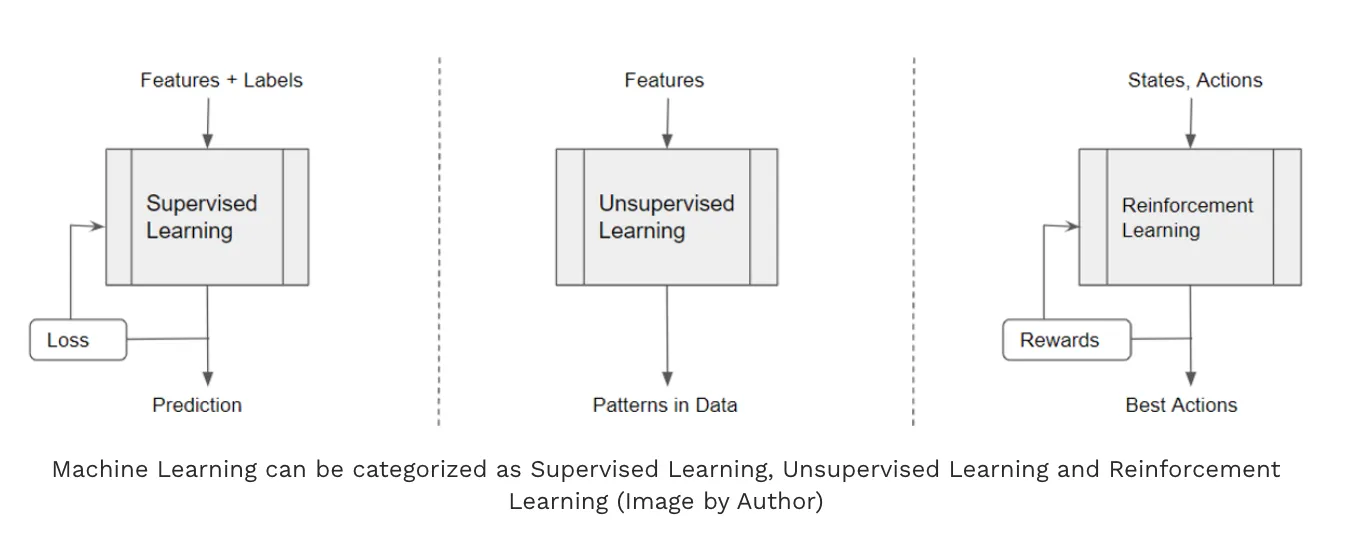
这些概念是要搞清楚的：

• 代理（Agent）
• 环境（Environment）
• 状态（state）
• 动作（action）
• 策略（policy）
• 轨迹（trajectory）
• 奖励（reward） 和 回报（Return）
• 状态价值函数（Value function）和 动作价值函数（Q-function）
• Value-based/Policy-based

细节请看：https://zhuanlan.zhihu.com/p/1929929237504198470

策略梯度

首先要明确RL的目标是什么， 目标就是去优化策略（$\pi$），使得回报（Return）的期望最大：

$$J(\theta )={\mathbb{E}}_{\tau \sim {\pi }_{\theta }}\left[R(\tau )\right]$$

这个期望是在整个轨迹$\tau$上，轨迹$\tau$指代一系列状态和动作，一个时间的序列：

$$\tau =(s_0,a_0,s_1,a_1,\dots )$$

策略梯度最终推导为：
$${\nabla }_{\theta }J(\theta )={\mathbb{E}}_{\tau \sim {\pi }_{\theta }}\left[\sum _{t=0}^{\infty }{\nabla }_{\theta }\log {\pi }_{\theta }(a_t|s_t)R(\tau )\right]$$

细节看：
https://zhuanlan.zhihu.com/p/1932820715456931793

REINFORCE

利用蒙特卡罗方法，多次采样来近似期望，策略梯度可以近似的写成：

$${\nabla }_{\theta }J(\theta )\approx \frac{1}{N}\sum _{i=1}^N\sum _{t=0}^{T_i-1}{\nabla }_{\theta }\log {\pi }_{\theta }\left(a_t^{(i)}\mid s_t^{(i)}\right)R\left({\tau }^{(i)}\right)$$

其中：

• $T_i$ 是第 $i$ 条轨迹 ${\tau }^{(i)}$ 的长度（因实际轨迹有限，求和到 $T_i-1$）；
• $a_t^{(i)}$ 和 $s_t^{(i)}$ 是第 $i$ 条轨迹中 $t$ 时刻的动作与状态；
• $R\left({\tau }^{(i)}\right)$ 是第 $i$ 条轨迹的总奖励。

通过两个方法来降低训练方差大的问题：

把Q函数和Advantage引入，则策略梯度可以写为：

$$\hat{g}=\frac{1}{N}\sum _{i=1}^N\sum _{t=0}^{T_i-1}{\nabla }_{\theta }\log {\pi }_{\theta }\left(a_t^{(i)}\mid s_t^{(i)}\right)\left(Q_{\pi }(s_t^{(i)},a_t^{(i)})-V_{\pi }(s_t^{(i)})\right)$$

其中Q-V则为advantage：
$$A_{\pi }(s,a)=Q_{\pi }(s,a)-V_{\pi }(s)$$

详细看：
https://zhuanlan.zhihu.com/p/1932820715456931793

RLOO

提出了基于REINFORCE的RLOO强化学习算法（REINFORCE Leave-One-Out)

相比于REINFORCE，RLOO核心实现细节在于，它采用批次中其他样本的平均奖励来计算基线，而不是对批次中的所有奖励取平均值。

对于RLOO基线，给定 $K$ 个采样轨迹或动作 $a_1,\dots ,a_K$，对于给定的提示 $s$，每个提示的基线为：

$$b(s,a_k)=\frac{1}{K-1}\sum _{\begin{array}{c}i=1,i\ne k\end{array}}^{K}r(s,a_i)$$

从而带来每个提示的优势：

$$A(s,a_k)=r(s,a_k)-b(s,a_k)$$

等效地，这可以表示为：

$$A(s,a_k)=\frac{K}{K-1}\left(r(s,a_k)-\frac{1}{K}\sum _{i=1}^{K}r(s,a_i)\right)$$

在RLOO中主要针对response-level的reward

详细看：
https://zhuanlan.zhihu.com/p/1932821169993675011

TRPO

策略梯度基本原理是利用梯度上升法朝着最大预期收益的方向优化。

然而，不合理的学习步长，会导致梯度上升法中的错误步骤可能导致次优操作，进而导致糟糕的状态。这反过来又会导致策略更新不佳和样本数据收集不佳。如此循环往复，最终可能导致策略性能崩溃，训练过程彻底失败。

需要了解：

通过KL散度限制以及重要性采样才优化。

最终的TRPO的优化等式为：
$$\begin{array}{rl}& \underset{\theta }{\mathrm{maximize}}{\mathbb{E}}_{s\sim {\rho }_{{\theta }_{\text{old}}}}{\mathbb{E}}_{a\sim {\pi }_{{\theta }_{\text{old}}}(a|s)}\left[\frac{{\pi }_{\theta }(a|s)}{{\pi }_{{\theta }_{\text{old}}}(a|s)}{A}_{{\theta }_{\text{old}}}(s,a)\right]\\ & \text{subject to}{\mathbb{E}}_{s\sim {\rho }_{{\theta }_{\text{old}}}}\left[D_{\text{KL}}({\pi }_{{\theta }_{\text{old}}}(\cdot |s)\Vert {\pi }_{\theta }(\cdot |s))\right]\le \delta \end{array}$$

详细看：
https://zhuanlan.zhihu.com/p/1934627686388588878

PPO

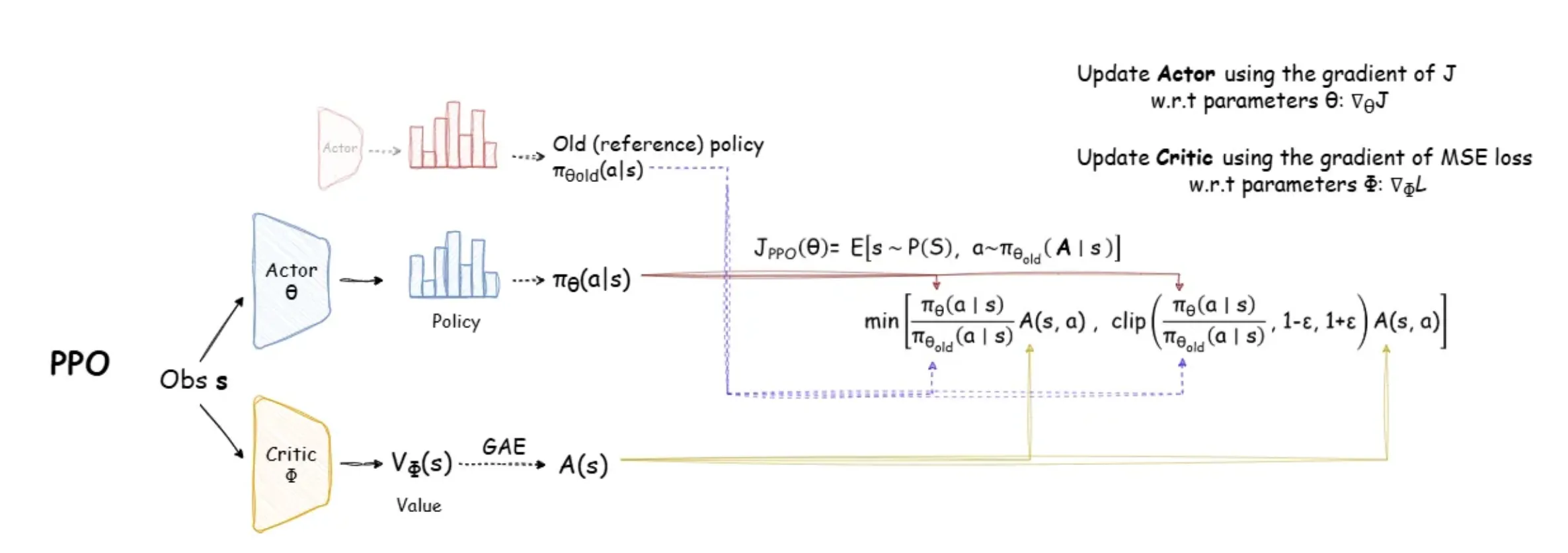
PPO基于GRPO继续优化。PPO方法实现要简单得多，且性能与TRPO相当。

有两种形式，其中效果更好的是Clip优化，
它依赖于目标函数中的专门Clip裁剪操作，以消除新策略远离旧策略的动机。

$$L_{ppo-clip}(\theta )={\hat{\mathbb{E}}}_t\left[\min (r_t(\theta ){\hat{A}}_t,\text{clip}(r_t(\theta ),1-ϵ,1+ϵ){\hat{A}}_t)\right]$$

其中$r_t(\theta )$为重要性采样部分：
$$r_t(\theta )=\frac{{\pi }_{\theta }(a_t|s_t)}{{\pi }_{{\theta }_{\text{old}}}(a_t|s_t)}$$

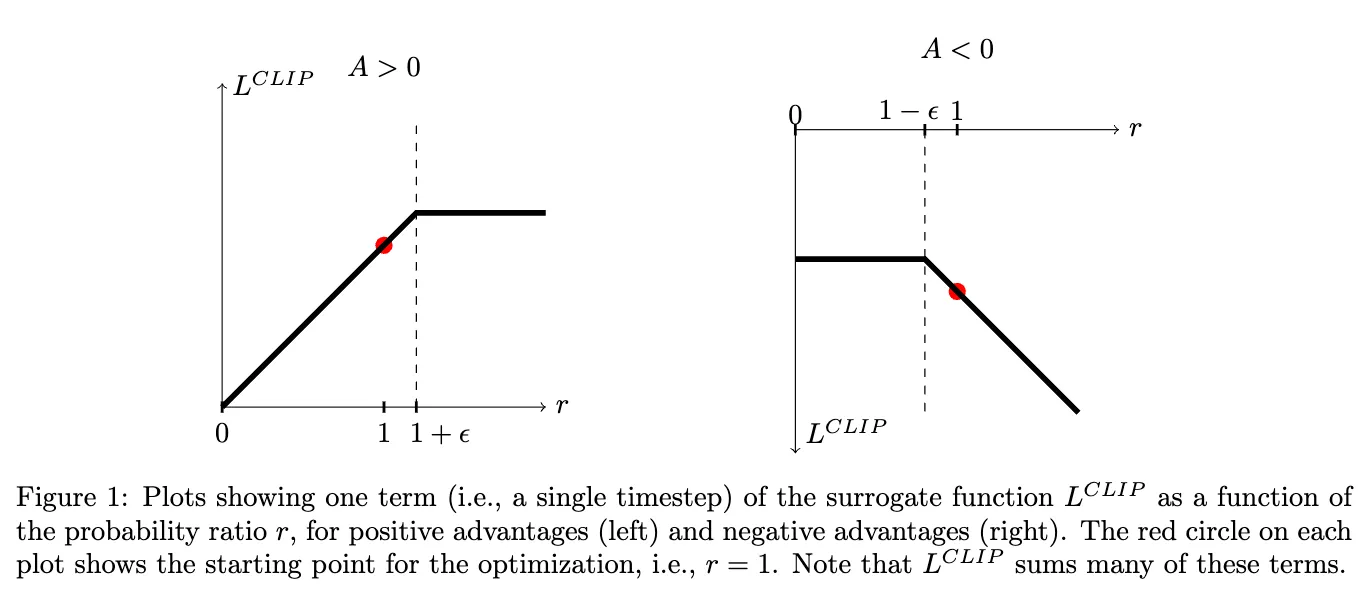
其中Advantage的估计采用了GAE方法进行估计，通过reward model的reward分数以及Value Model估计的期望回报计算残差进行估计。详细的GAE方法可见：https://zhuanlan.zhihu.com/p/1934626865701720143

PPO的公式和代码解读可以看：
https://zhuanlan.zhihu.com/p/1937882242291598044

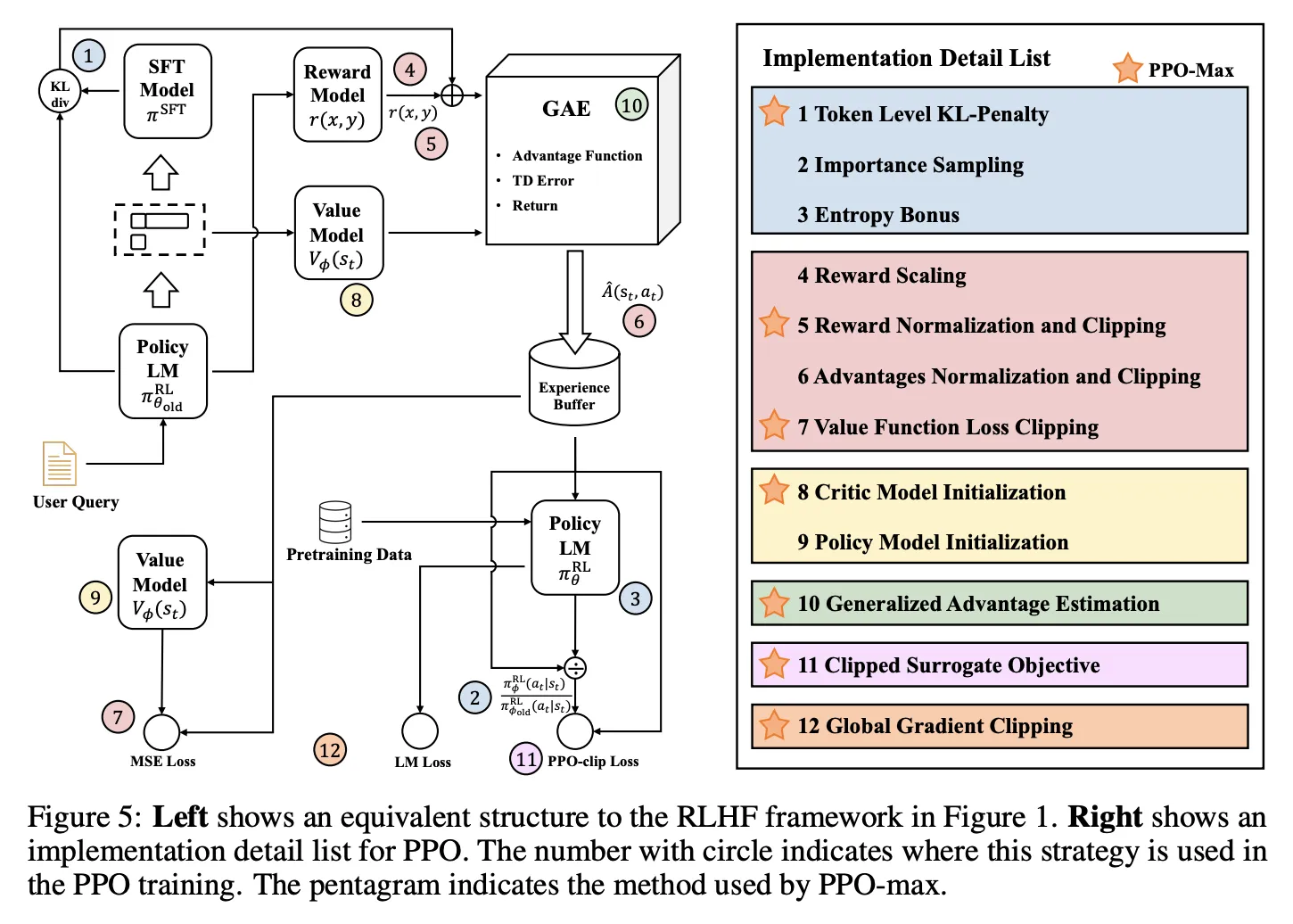
PPO训练的稳定技巧（参考：https://zhuanlan.zhihu.com/p/1937885098239325591）：

GRPO

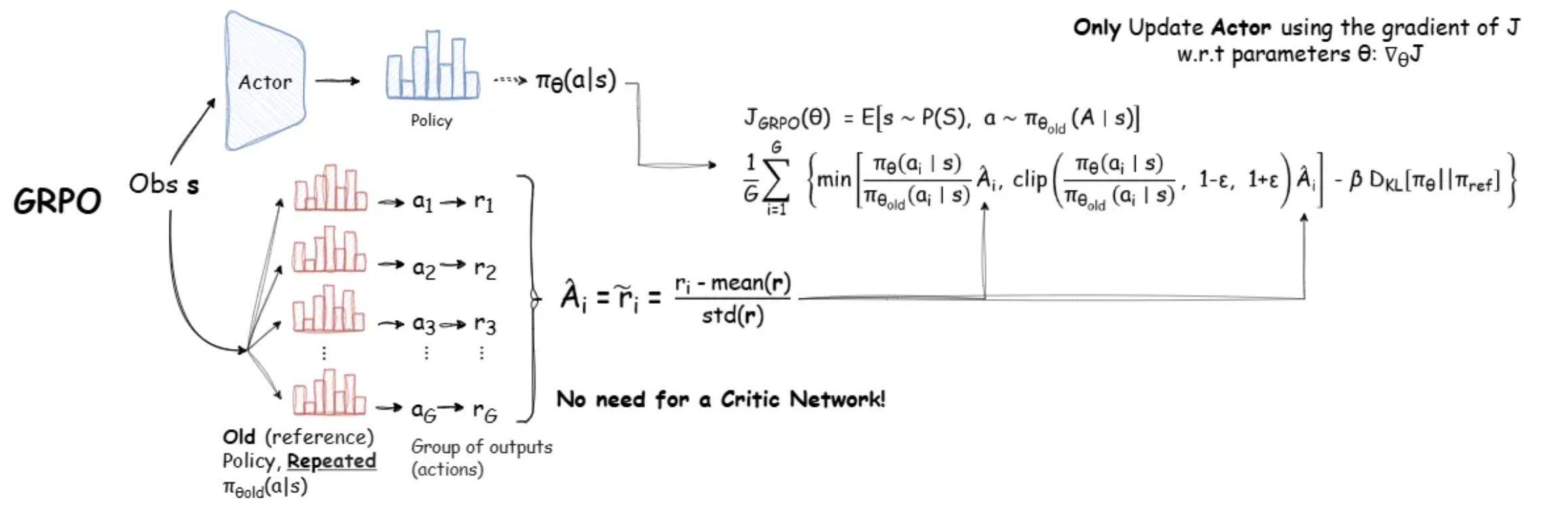
采样多个输出的平均reward作为baseline，而不用单独的Value Model去预测baseline，节省了Value Model，从而显著的减少了训练资源的使用。

作为基线，用于回答相同问题。对于每个问题 $q$，从旧策略${\pi }_{{\theta }_{\text{old}}}$ 中采样一组输出 $ {o_1, o_2, \\cdots, o_G}$，然后通过最大化以下目标来优化策略模型：

$$\begin{array}{rl}{\mathcal{J}}_{\text{GRPO}}(\theta )& =\mathbb{E}\left[q\sim P(Q),\{o_i{\}}_{i=1}^G\sim {\pi }_{{\theta }_{\text{old}}}(O|q)\right]\\ & \frac{1}{G}\sum _{i=1}^G\frac{1}{|o_i|}\sum _{t=1}^{|o_i|}\left\{\min \left[\frac{{\pi }_{\theta }(o_{i,t}|q,o_{i,<t})}{{\pi }_{{\theta }_{\text{old}}}(o_{i,t}|q,o_{i,<t})}{\hat{A}}_{i,t},\text{clip}\left(\frac{{\pi }_{\theta }(o_{i,t}|q,o_{i,<t})}{{\pi }_{{\theta }_{\text{old}}}(o_{i,t}|q,o_{i,<t})},1-\epsilon ,1+\epsilon \right){\hat{A}}_{i,t}\right]-\beta {\mathbb{D}}_{\text{KL}}\left[{\pi }_{\theta }\Vert {\pi }_{\text{ref}}\right]\right\}\end{array}$$

其中 $ \\varepsilon $ 和 $ \\beta $ 是超参数，$ \\hat{A}_{i,t} $ 是仅基于每组内部输出的相对奖励计算的优势。

GRPO使用无偏估计来估计 KL 散度：
$${\mathbb{D}}_{KL}\left[{\pi }_{\theta }\Vert {\pi }_{\text{ref}}\right]=\frac{{\pi }_{\text{ref}}(o_{i,t}\mid q,o_{i,<t})}{{\pi }_{\theta }(o_{i,t}\mid q,o_{i,<t})}-\log \frac{{\pi }_{\text{ref}}(o_{i,t}\mid q,o_{i,<t})}{{\pi }_{\theta }(o_{i,t}\mid q,o_{i,<t})}-1,$$

这个值一定为正。

解读参考： https://zhuanlan.zhihu.com/p/1938204409831069009