相控阵天线（3）——平面相控阵天线原理

1.平面阵列概念

        平面阵列是线性阵列的自然延伸。平面阵列具有很多配置，取决于单元的间隔和所定义“网格”的分布。例子包括矩形的、圆形边界矩形的、圆形边界六边形的、圆形的、同轴圆形的网格，如图1所示。

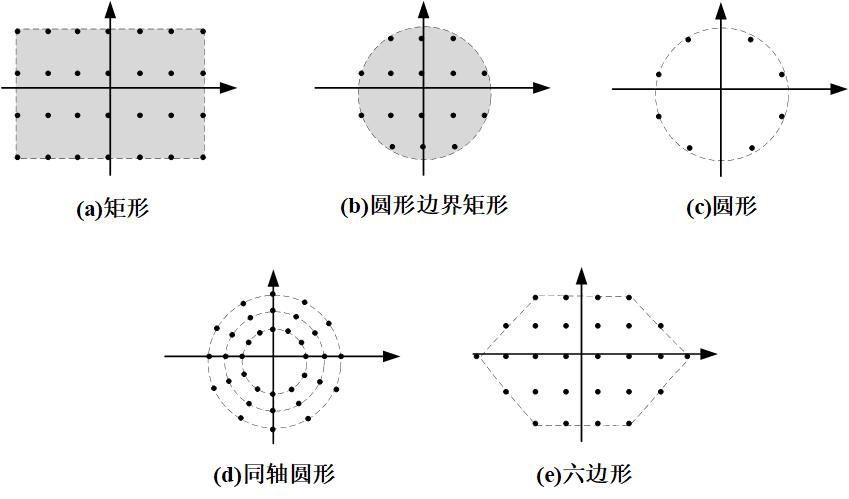
图1  平面网格阵列

2.矩形网格阵列

      平面阵列可以在仰角和方位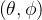上扫描，图2所示为矩形网格阵列。沿着x方向和y方向的单元间隔各自表示为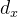、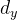。通过《相控阵天线（1）——天线参数及一维线性阵列天线原理_相控阵的天线增益-CSDN博客》中对一维线性阵列天线的理论分析，可推导任意平面天线在远场观测点处总的电场表达为：

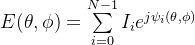（1）

       假设平面阵列由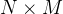个天线单元组成，每个单元在x-y平面上按矩形网格排列，坐标为 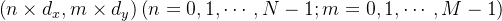，如图2所示。设第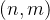个单元的激励电流为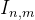，相邻单元之间相位延迟为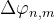，则远场观测点处的电场可线性分解为它的x、y分量。可以得到单元沿着x、y方向分布的电场分量为：

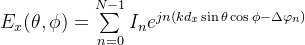（2）

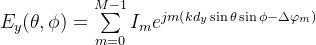（3）

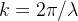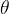其中，为波数，为仰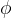角， 为方位角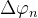，为相邻单元之间在x方向上的相位延迟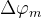，为相邻单元之间在y方向上的相位延迟。则远场观测点处的总电场表示为各单元电场的矢量叠加：

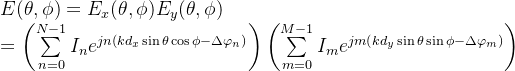（4）

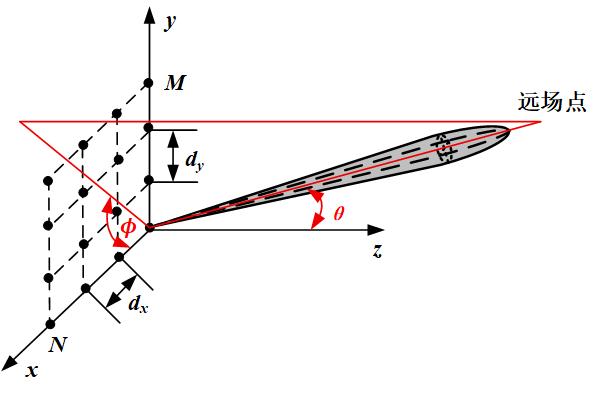
图2  平面矩形阵列示意图

       矩形阵列的单程强度方向图等于各自方向图的乘积。根据《相控阵天线（1）——天线参数及一维线性阵列天线原理_相控阵的天线增益-CSDN博客》中公式（15）可知，对于均衡的激励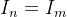，可得：

（5）

3.矩形网格阵列相控阵天线方向图特性分析

       辐射方向图的最大值、零点、副瓣、栅瓣在x轴、y轴上的计算和线性阵列的情况是相似的。另外，栅瓣控制的同样条件是可以应用的。注意，角度是对称的。以下结合《相控阵天线（2）一维线性阵列特性-CSDN博客》的内容，对平面相控阵天线方向图特性进行分析。

①波束调向

       当式（5）中, 时，函数取得最大值1，此时可得到天线方向图的最大值，能量集中的最强波瓣，即主瓣，此时相位延迟∆φn,m需满足：

（6）

②波束宽度

      将波数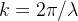以及式（6）中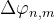与波束指向之间的关系代入原式（5）中，可得：

（7）

波束指向为天线阵面法线方向时的宽度，这时，即，为各阵元等幅同相馈电情况。由式(4)可得方向性函数为

（8）

      通常情况下，波束很窄，、很小，，，在 x 、y方向，上式变为：

（9）

（10）

上式近似为辛克(sinc)函数，当取(即A = 1.39)时，得到天线波瓣的半功率点位置，在 x 方向，半功率波束宽度近似为：

（11）

       y 方向半功率波束宽度公式类似： 

（12）

表明增大阵列规模或减小扫描角可压缩波束宽度，提高方向性。

③旁瓣与栅瓣

       理想情况下，平面相控阵可在、范围内扫描，但实际受很多因素限制。当扫描角增大时，等效单元间距在波前方向的投影增大，易激发栅瓣。通常要求扫描范围内且，限制最大扫描角约为 60°~70°。