论文翻译与解读——雷达阵列信号处理中的最大似然方法

雷达阵列信号处理中的最大似然方法

A. L. Swindlehurst and P. Stoica, “Maximum likelihood methods in radar array signal processing,” in Proceedings of the IEEE, vol. 86, no. 2, pp. 421-441, Feb. 1998, doi: 10.1109/5.659495.

本文探讨了在雷达目标信号被传感器阵列观测时，如何在未知二阶统计特性的干扰环境中，使用鲁棒且计算高效的最大似然算法来估计目标参数。文章提出了两种数据模型：一种使用目标到达方向和信号幅度作为参数，另一种是使用通用目标"空间特征"的简化非结构化模型。通过引入扩展不变性原理，展示了如何将从简单模型获得的较不精确的最大似然估计进行改进，以渐近地达到使用结构化模型所能获得的性能。

引言

在主动雷达系统中，主要目标是在噪声、地杂波和电子对抗措施（如干扰）存在的情况下检测目标并估计其参数。对于机载雷达应用，感兴趣的参数包括目标信号幅度（与其雷达截面积相关）、到达方向（DOA）、距离和多普勒频率。即使只有单个目标存在，由于需要搜索的参数空间体积巨大，这个检测和估计问题也相当艰巨。因此，计算的简便性和效率至关重要。

标准解决方案涉及使用经典的时空滤波器，可以是数据无关的（如延迟求和波束形成器）或"自适应"的（如使用线性约束、最大信号干扰噪声比准则等）。最大似然（ML）方法在这个问题上没有被广泛考虑，主要是因为它们被认为计算过于复杂，而且在接受所需的建模假设方面存在一些阻力。最近的工作表明，对于高斯干扰中具有未知空间协方差的单个目标源，ML解可以通过对目标DOA和多普勒进行二维搜索，然后进行广义似然比检验（GLRT）来获得。

雷达数据模型

结构化阵列模型

假设一个$m$元天线阵列使用某组发射权重发射一系列脉冲。在给定的相干处理间隔（CPI）期间，存在于特定距离单元中的目标可以建模为产生以下基带向量信号（经过脉冲压缩和解调后）：

$$\text{target signal}=b_0\mathbf{a}({\theta }_0)e^{j{\omega }_{0}t},t=1,\cdots ,N$$

其中$b_0$是信号的复振幅，${\omega }_0$是由阵列平台和目标之间的相对运动引起的多普勒频移，$\mathbf{a}(\theta )$是阵列对从方位角${\theta }_0$到达的平面波的响应。向量$\mathbf{a}(\theta )$被假定为缩放，使得其第一个元素对所有$\theta$都为1。

假设在任何给定的距离单元中最多存在一个目标，阵列在时间$t$的采样向量输出或"快照"可以写成：

$$\mathbf{x}(t)=b_0\mathbf{a}({\theta }_0)e^{j{\omega }_{0}t}+\mathbf{e}(t)\in {\mathbb{C}}^m,t=1,\cdots ,N$$

其中如果没有目标存在则$b_0$取为零，$\mathbf{e}(t)$表示由于杂波、接收机噪声和干扰引起的干扰。由于$\mathbf{e}(t)$依赖于如此多的物理变量，为其推导确定性模型是有问题的，通常也是不实际的。首先，我们选择将$\mathbf{e}(t)$建模为在CPI的$N$个样本上的平稳、时间白性高斯随机过程，具有零均值和未知空间协方差$\mathbf{Q}$。

非结构化阵列模型

在上面的讨论中，我们已经明确地用${\theta }_0$来表示阵列响应。当然，要估计${\theta }_0$，向量值函数$\mathbf{a}(\theta )$必须对所有感兴趣的$\theta$都是已知的。函数$\mathbf{a}(\theta )$可以通过阵列的实验或分析校准获得，但这种校准程序永远不会完全准确，这是由于天线元件的增益和相位响应误差、互耦、量化和插值误差，以及由于天气、环境等变化导致的接收机电子特性漂移。根据实际阵列响应与其模型的差异程度，检测和估计性能可能会显著下降。出于这个原因，我们在非结构化阵列模型下开发了目标检测的GLRT，该模型本质上不依赖于阵列校准数据的可用性。考虑以下数据模型，其中信号幅度和阵列响应已合并为单个非结构化向量项：

$$\mathbf{x}(t)={\mathbf{\alpha }}_0{e}^{j{\omega }_{0}t}+\mathbf{e}(t),t=1,\cdots ,N$$

向量${\mathbf{\alpha }}_0$被称为目标的"空间特征"，在这个模型中取代了$b_0\mathbf{a}({\theta }_0)$，简单地被视为一组未知的复常数。

扩展不变性原理

假设为了估计上述雷达参数，我们有一个损失函数（例如，ML准则），可以用$\mathbf{\eta }$或$\tilde{\mathbf{\eta }}$参数化。将得到的准则分别表示为$V_N(\mathbf{\eta })$和${\tilde{V}}_N(\tilde{\mathbf{\eta }})$。如果存在一个（可逆的）映射$\mathbf{\eta }=g(\tilde{\mathbf{\eta }})\in D_{\eta },\forall \tilde{\mathbf{\eta }}\in D_{\tilde{\eta }}$，使得准则相等，经典的估计理论不变性原理可以被调用来证明最小化$V_N(\mathbf{\eta })$和${\tilde{V}}_N(\tilde{\mathbf{\eta }})$的等价性。

扩展不变性原理（EXIP）通过以下定理给出：

定理1：定义
$$\hat{\mathbf{\eta }}=\arg \underset{\mathbf{\eta }}{\min }{V}_N(\mathbf{\eta })$$
$$\widehat{\tilde{\mathbf{\eta }}}=\arg \underset{\tilde{\mathbf{\eta }}}{\min }{\tilde{V}}_N(\tilde{\mathbf{\eta }})$$

并假设存在满足$\tilde{\mathbf{\eta }}=f(\mathbf{\eta })\in D_{\tilde{\eta }},\forall \mathbf{\eta }\in D_{\eta }$的函数$f$。假设$f$在其输入参数的整个定义域上是一对一的且定义良好。如果${\lim }_{N\to \infty }\widehat{\tilde{\mathbf{\eta }}}={\lim }_{N\to \infty }f(\hat{\mathbf{\eta }})$，则

$$\hat{\mathbf{\eta }}=\arg \underset{\mathbf{\eta }}{\min }[\widehat{\tilde{\mathbf{\eta }}}-f(\mathbf{\eta }){]}^T\mathbf{W}[\widehat{\tilde{\mathbf{\eta }}}-f(\mathbf{\eta })]$$

渐近地（对于大$N$）等价于估计$\hat{\mathbf{\eta }}$，其中

$$\mathbf{W}=\mathcal{E}{\left\{\frac{\partial {\tilde{V}}_N(\widehat{\tilde{\mathbf{\eta }}})}{\partial \widehat{\tilde{\mathbf{\eta }}}\partial {\widehat{\tilde{\mathbf{\eta }}}}^T}\right\}}_{\widehat{\tilde{\mathbf{\eta }}}=\tilde{\mathbf{\eta }}}$$

最大似然估计

结构化模型

完全参数化模型的$N$个数据样本的负对数似然函数在乘法和加法常数内容易表示为：

$$V_N(\mathbf{\eta })=\log |\mathbf{Q}|+\text{Tr}\{{\mathbf{Q}}^{-1}\mathbf{C}(b,\theta ,\omega )\}$$

其中
$$\mathbf{C}(b,\theta ,\omega )=\frac{1}{N}\sum _{t=1}^N[\mathbf{x}(t)-b\mathbf{a}(\theta )e^{j\omega t}][\mathbf{x}(t)-b\mathbf{a}(\theta )e^{j\omega t}{]}^{\ast }$$

关于$\mathbf{Q}$和$b$的最小化可以显式执行。使用标准矩阵微积分结果，关于$\mathbf{Q}$的准则梯度容易表示为：

$$\frac{\partial V_N(\mathbf{\eta })}{\partial \mathbf{Q}}={\mathbf{Q}}^{-1}-{\mathbf{Q}}^{-1}\mathbf{C}(b,\theta ,\omega ){\mathbf{Q}}^{-1}$$

从中可以清楚地看出，$\mathbf{Q}$的ML估计由下式给出：
$${\hat{\mathbf{Q}}}_s=\mathbf{C}(b,\theta ,\omega )$$

当将此代入准则时，集中准则为：
$$V_N(b,\theta ,\omega )=\log |\mathbf{C}(b,\theta ,\omega )|+m$$

可以进一步关于$b$集中，得到：
$${\hat{b}}_s=\frac{{\mathbf{a}}^{\ast }({\hat{\theta }}_s){\hat{\mathbf{R}}}_s^{-1}\mathbf{y}({\hat{\omega }}_s)}{{\mathbf{a}}^{\ast }({\hat{\theta }}_s){\hat{\mathbf{R}}}_s^{-1}\mathbf{a}({\hat{\theta }}_s)}$$

$${\hat{\theta }}_s,{\hat{\omega }}_s=\arg \underset{\theta ,\omega }{\max }\frac{|{\mathbf{a}}^{\ast }(\theta ){\hat{\mathbf{R}}}^{-1}\mathbf{y}(\omega ){|}^2}{[1-{\mathbf{y}}^{\ast }(\omega ){\hat{\mathbf{R}}}^{-1}\mathbf{y}(\omega )][{\mathbf{a}}^{\ast }(\theta ){\hat{\mathbf{R}}}^{-1}\mathbf{a}(\theta )]}$$

其中
$$\mathbf{y}(\omega )=\frac{1}{N}\sum _{t=1}^N\mathbf{x}(t)e^{-j\omega t}$$
$${\hat{\mathbf{R}}}_s=\hat{\mathbf{R}}-\mathbf{y}(\omega ){\mathbf{y}}^{\ast }(\omega )$$
$$\hat{\mathbf{R}}=\frac{1}{N}\sum _{t=1}^N\mathbf{x}(t){\mathbf{x}}^{\ast }(t)$$

非结构化模型

非结构化模型的ML解可以类似地推导。$\tilde{\mathbf{\eta }}$的负对数似然函数具有与结构化情况相同的形式，但用$\mathbf{\alpha }$替换$b\mathbf{a}(\theta )$。关于$\mathbf{\alpha }$的最小化给出：

$${\hat{\mathbf{\alpha }}}_u=\mathbf{y}(\omega )$$

其中下标$u$用于明确表示使用非结构化模型获得的估计。将此代入准则并简化后，$\omega$的解简单地为：

$${\hat{\omega }}_u=\arg \underset{\omega }{\max }{\mathbf{y}}^{\ast }(\omega ){\hat{\mathbf{R}}}^{-1}\mathbf{y}(\omega )$$

因此，非结构化ML估计$\omega$由下式给出：
$${\hat{\omega }}_u=\arg \underset{\omega }{\max }{\mathbf{y}}^{\ast }(\omega ){\hat{\mathbf{R}}}^{-1}\mathbf{y}(\omega )$$

使用EXIP进行参数估计

根据定理4，给定从非结构化模型获得的${\hat{\mathbf{Q}}}_u$、${\hat{\mathbf{\alpha }}}_u$和${\hat{\omega }}_u$，雷达目标参数的渐近（在$N$中）有效估计可以如下找到：

$${\hat{\mathbf{Q}}}_e={\hat{\mathbf{Q}}}_u$$
$${\hat{\omega }}_e={\hat{\omega }}_u$$

$${\hat{b}}_e,{\hat{\theta }}_e=\arg \underset{b,\theta }{\min }{\left[\left(\begin{array}{c}({\hat{\mathbf{\alpha }}}_u{)}_r\\ ({\hat{\mathbf{\alpha }}}_u{)}_i\end{array}\right)-\mathbf{A}(\theta )\left(\begin{array}{c}{b}_r\\ b_i\end{array}\right)\right]}^T\cdot {\mathbf{W}}_Q\left[\left(\begin{array}{c}({\hat{\mathbf{\alpha }}}_u{)}_r\\ ({\hat{\mathbf{\alpha }}}_u{)}_i\end{array}\right)-\mathbf{A}(\theta )\left(\begin{array}{c}{b}_r\\ b_i\end{array}\right)\right]$$

其中
$${\mathbf{W}}_Q=2N\left[\begin{array}{cc}\text{Re}\{{\hat{\mathbf{Q}}}_u^{-1}\}& -\text{Im}\{{\hat{\mathbf{Q}}}_u^{-1}\}\\ \text{Im}\{{\hat{\mathbf{Q}}}_u^{-1}\}& \text{Re}\{{\hat{\mathbf{Q}}}_u^{-1}\}\end{array}\right]$$

$$\mathbf{A}(\theta )=\left[\begin{array}{cc}\text{Re}\{\mathbf{a}(\theta )\}& -\text{Im}\{\mathbf{a}(\theta )\}\\ \text{Im}\{\mathbf{a}(\theta )\}& \text{Re}\{\mathbf{a}(\theta )\}\end{array}\right]$$

可以显式求解${\hat{b}}_e$，得到仅依赖于$\theta$的准则：

$${\hat{b}}_e=\frac{{\mathbf{a}}^{\ast }({\hat{\theta }}_e){\hat{\mathbf{Q}}}_u^{-1}{\hat{\mathbf{\alpha }}}_u}{{\mathbf{a}}^{\ast }({\hat{\theta }}_e){\hat{\mathbf{Q}}}_u^{-1}\mathbf{a}({\hat{\theta }}_e)}$$

$${\hat{\theta }}_e=\arg \underset{\theta }{\max }\frac{|{\mathbf{a}}^{\ast }(\theta ){\hat{\mathbf{Q}}}_u^{-1}{\hat{\mathbf{\alpha }}}_u{|}^2}{{\mathbf{a}}^{\ast }(\theta ){\hat{\mathbf{Q}}}_u^{-1}\mathbf{a}(\theta )}$$

检测

在本节中，我们讨论在确定给定数据集中是否存在目标时出现的二元假设检验问题。特别是，需要决定以下两个假设中哪一个对$\mathbf{x}(t),t=1,\cdots ,N$有效：

$$H_0:\mathbf{x}(t)=\mathbf{e}(t)$$
$$H_1:\mathbf{x}(t)=b_0\mathbf{a}({\theta }_0)e^{j{\omega }_{0}t}+\mathbf{e}(t)$$

结构化模型的GLRT

如果$p_{H_0}$和$p_{H_1}$表示对应于两个假设的数据概率密度，结构化ML模型的GLRT可以表述为：

$$\lambda =\frac{p_{H_1}(\mathbf{x}(1),\cdots ,\mathbf{x}(N)|{\hat{b}}_s,{\hat{\theta }}_s,{\hat{\omega }}_s,{\hat{\mathbf{Q}}}_s)}{p_{H_0}(\mathbf{x}(1),\cdots ,\mathbf{x}(N)|{\hat{\mathbf{Q}}}_s)}\underset{H_0}{\stackrel{H_1}{\gtrless }}{\lambda }_T$$

其中${\hat{b}}_s,{\hat{\theta }}_s,{\hat{\omega }}_s,{\hat{\mathbf{Q}}}_s$是结构化ML估计，${\lambda }_T$是某个阈值。由于$H_0$和$H_1$下的数据都是高斯的，通常取两边的对数，此时GLRT形式为：

$$\lambda =2\log {\lambda }^{\prime }=2N(\log |\hat{\mathbf{R}}|-\log |\mathbf{C}({\hat{b}}_s,{\hat{\theta }}_s,{\hat{\omega }}_s)|)\underset{H_0}{\stackrel{H_1}{\gtrless }}2\log {\lambda }_T={\lambda }_T^{\prime }$$

非结构化模型的GLRT

对于非结构化模型，两个竞争假设是：
$$H_0:\mathbf{x}(t)=\mathbf{e}(t)$$
$$H_1^u:\mathbf{x}(t)={\mathbf{\alpha }}_0{e}^{j{\omega }_{0}t}+\mathbf{e}(t)$$

得到的GLRT在形式上类似于结构化情况，用${\hat{\mathbf{\alpha }}}_u$替换${\hat{b}}_s,{\hat{\theta }}_s$：

$${\lambda }_u=2N(\log |\hat{\mathbf{R}}|-\log |\mathbf{C}({\hat{\mathbf{\alpha }}}_u,{\hat{\omega }}_u)|)\underset{H_0}{\stackrel{H_1}{\gtrless }}{\lambda }_{T_u}$$

从前面的推导可知：
$$\log |\mathbf{C}({\hat{\mathbf{\alpha }}}_u,{\hat{\omega }}_u)|=\log (1-z_R({\hat{\omega }}_u))+\log |\hat{\mathbf{R}}|$$

因此问题是确定${\lambda }_{T_u}$使得：
$${\lambda }_u=-2N\log (1-z_R({\hat{\omega }}_u))>{\lambda }_{T_u}$$

在$H_0$下以给定的PFA $P_f$发生。由于对数是单调的，不等式等价于条件：
$$2N{z}_R({\hat{\omega }}_u)>2N(1-\exp (-{\lambda }_{T_u}/2N))$$

对于大$N$可以进一步近似为：
$$2N{z}_R({\hat{\omega }}_u)>{\lambda }_{T_u}$$

仿真结果

渐近性验证

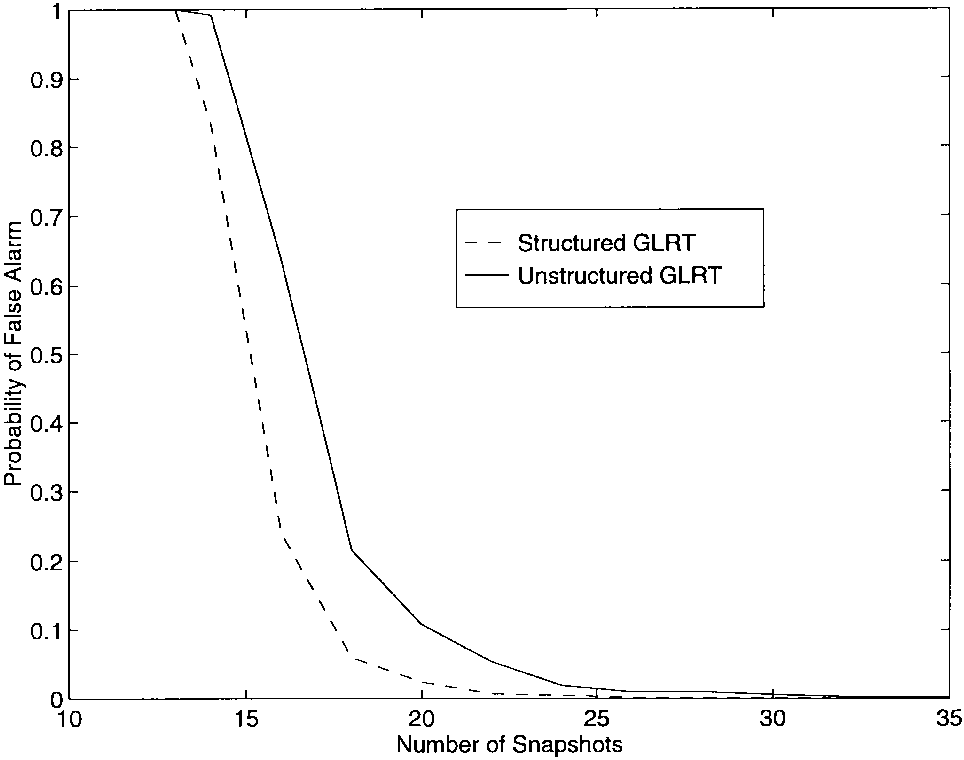
图1显示了在没有信号存在时，结构化和非结构化GLRT的PFA与从阵列获取的快照数的关系。结果基于每个$N$值的1000次试验。虽然两个测试都随着$N$的增加接近低PFA值，但结构化GLRT的"阈值"似乎比非结构化GLRT小几个（两到三个）快照。

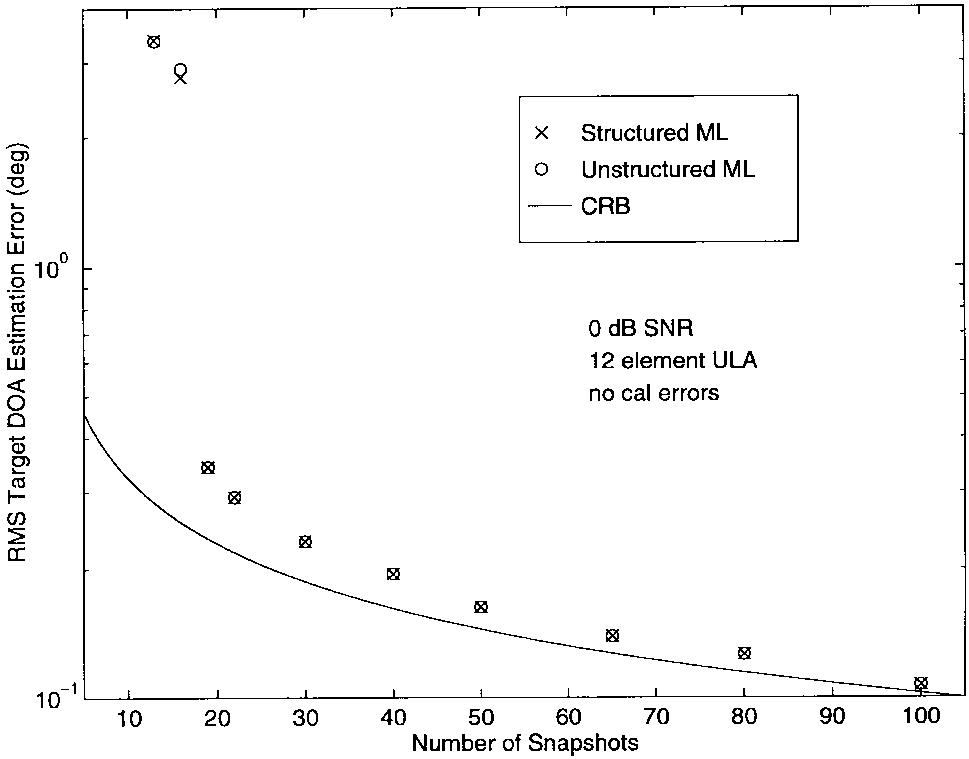
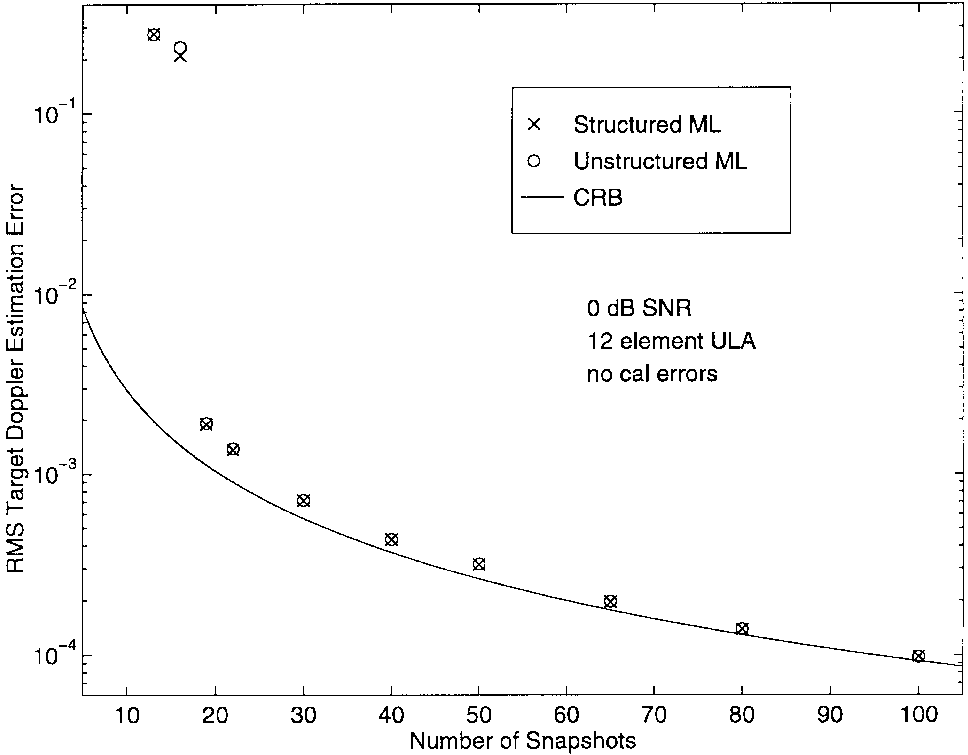
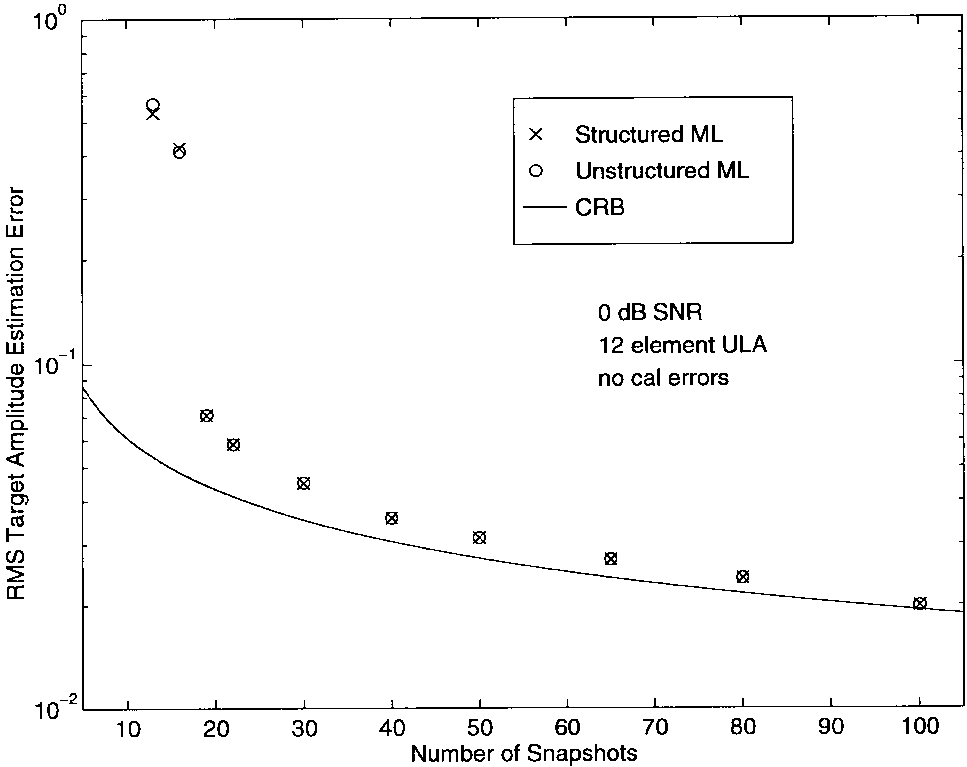
图2-4分别显示了DOA、多普勒和幅度估计的均方根（rms）误差与$N$的关系，针对0-dB SNR和理想阵列（无校准误差）的情况。从图中可以清楚地看出，对于所有$N$值，SML和UML估计的质量基本上没有差异。因此，至少对于这些情况，两种方法的渐近等价性在数据很少的情况下就很明显。

鲁棒检测

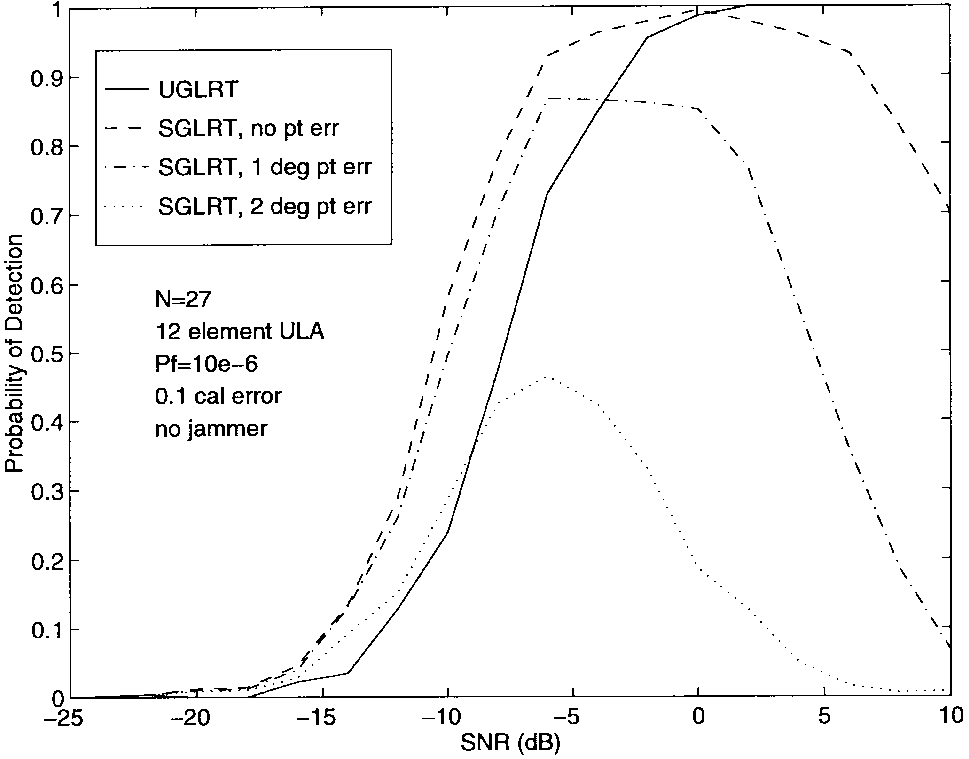
图5比较了在各种SNR下SGLRT和UGLRT的检测概率（每个SNR 500次试验），针对校准误差为0.1的阵列情况。SGLRT的三条曲线显示了其在"指向"误差为0°、1°和2°时的性能。图5表明SGLRT对${\theta }_t={\theta }_0$的假设非常敏感。当然，UGLRT不会遇到这种困难，因为它不使用DOA信息。

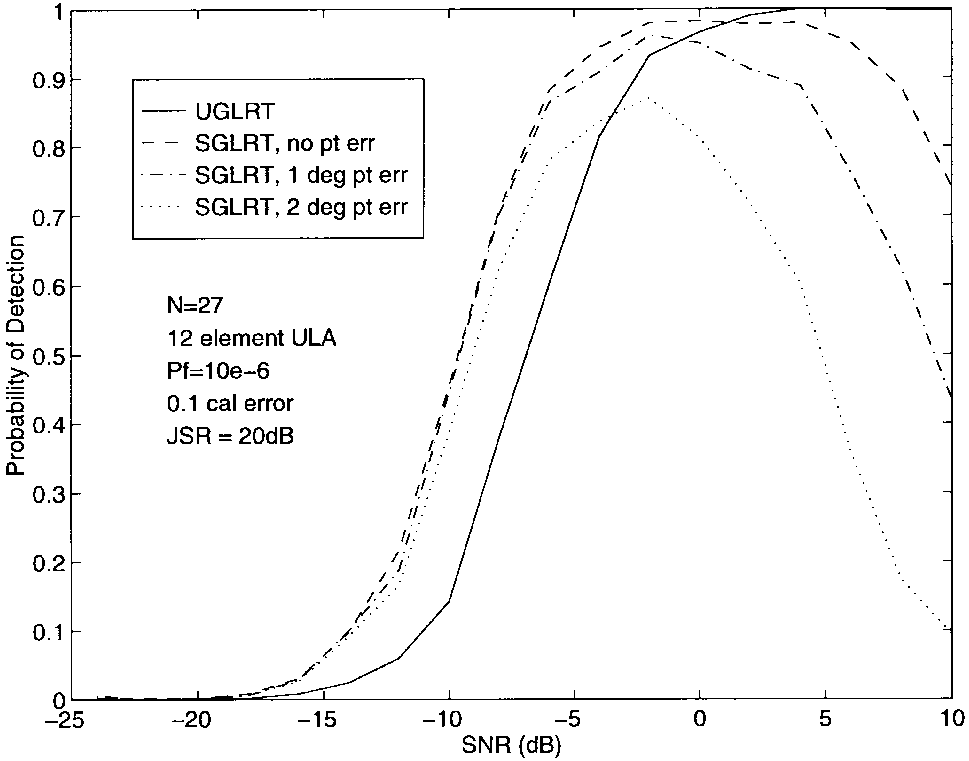
在数据中添加了强干扰器后重复了上述实验，结果绘制在图6中。干扰器位于5°的DOA，干扰信号比（JSR）固定为20 dB。干扰器的存在导致低SNR时检测概率略有降低，但似乎在较高SNR时提高了SGLRT的性能。然而，这种改进只是人为的，因为干扰器的随机贡献推动了检测准则的峰值超过阈值。

鲁棒估计

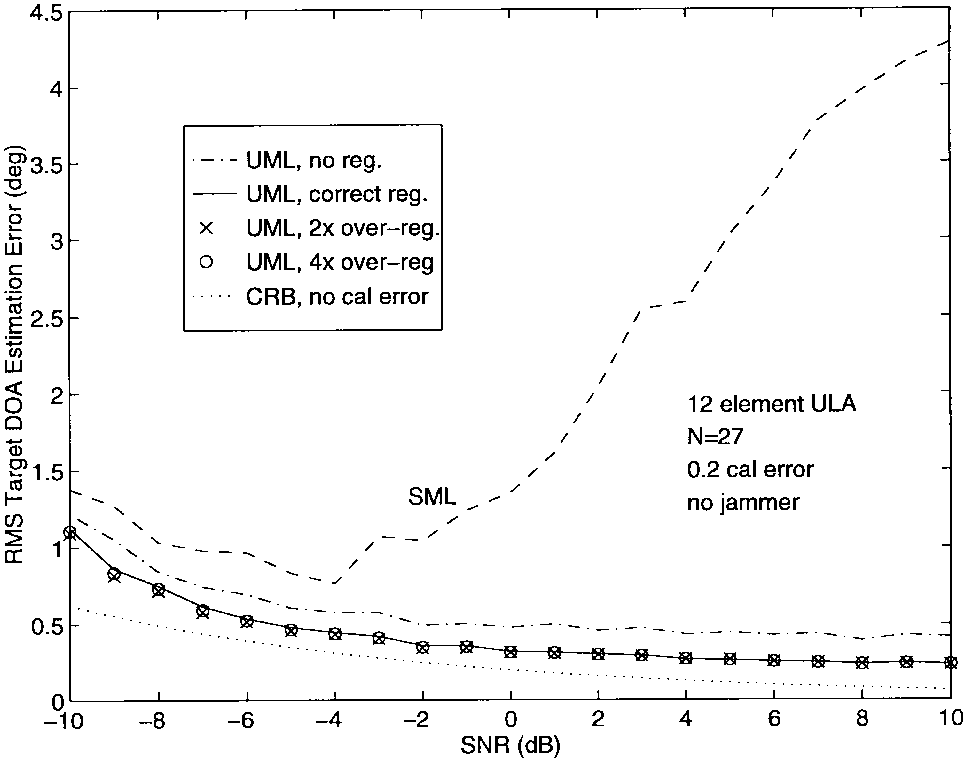
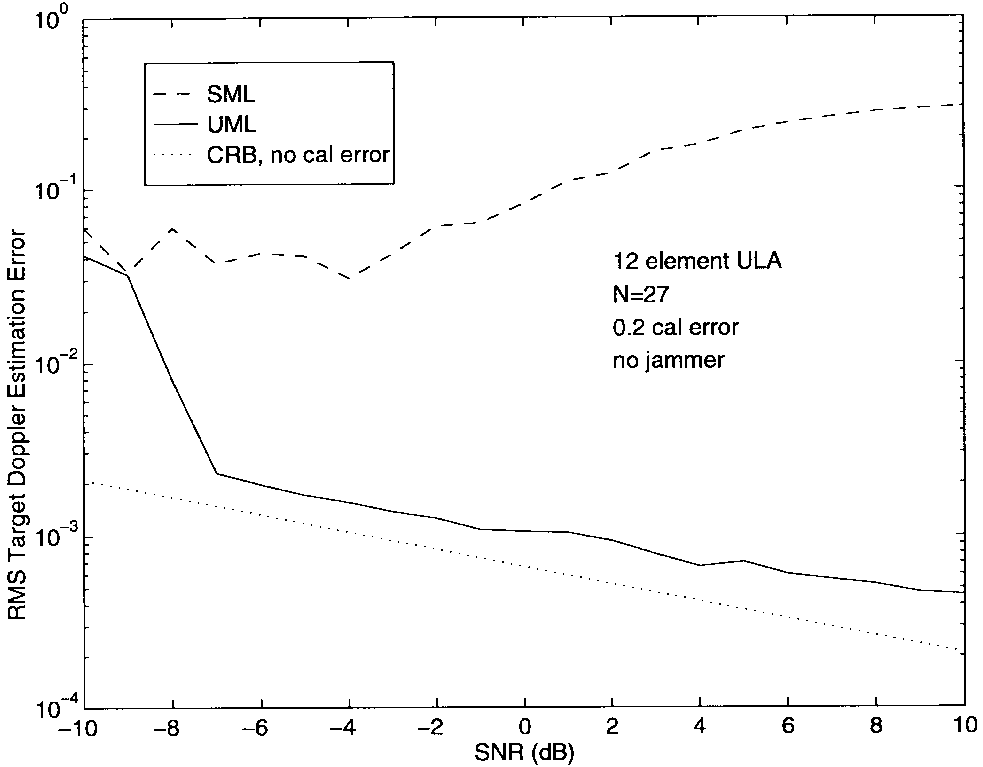
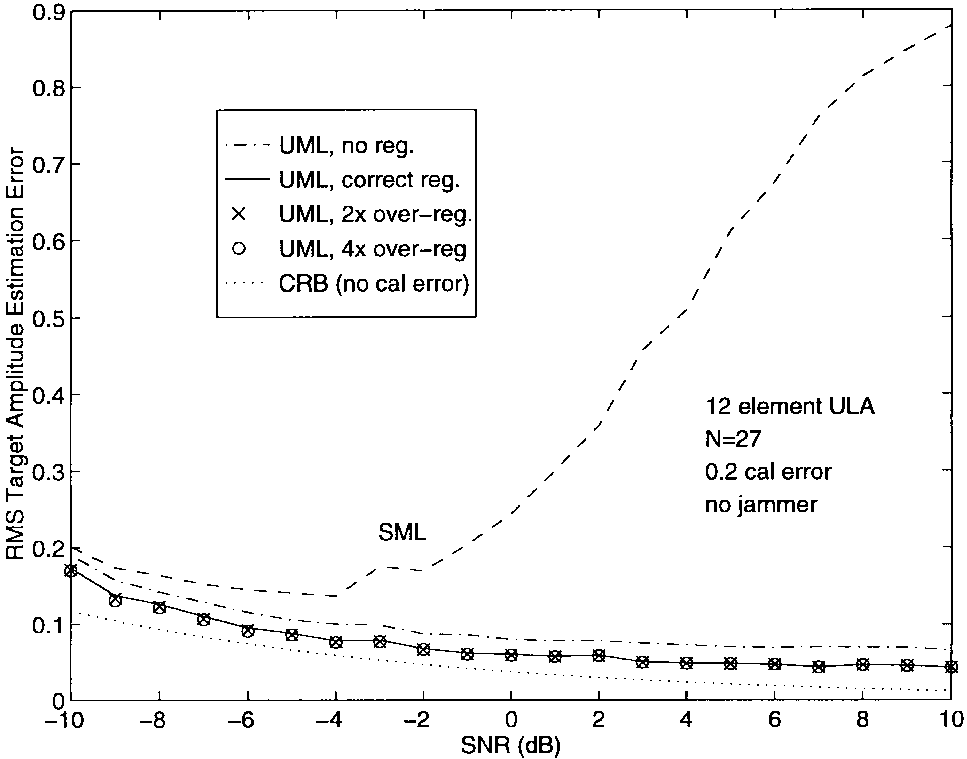
图7-9显示了在没有干扰器存在时，目标DOA、多普勒和幅度估计的rms误差与SNR的关系。图中的虚线表示使用标准加权的UML性能。实线给出了正确加权的结果。图上的符号"x"和"o"对应于正则化UML的结果，分别实现了${\sigma }_a$被高估2倍和4倍的情况。可以看出，正则化提供的性能改进对该参数的确切知识非常不敏感。

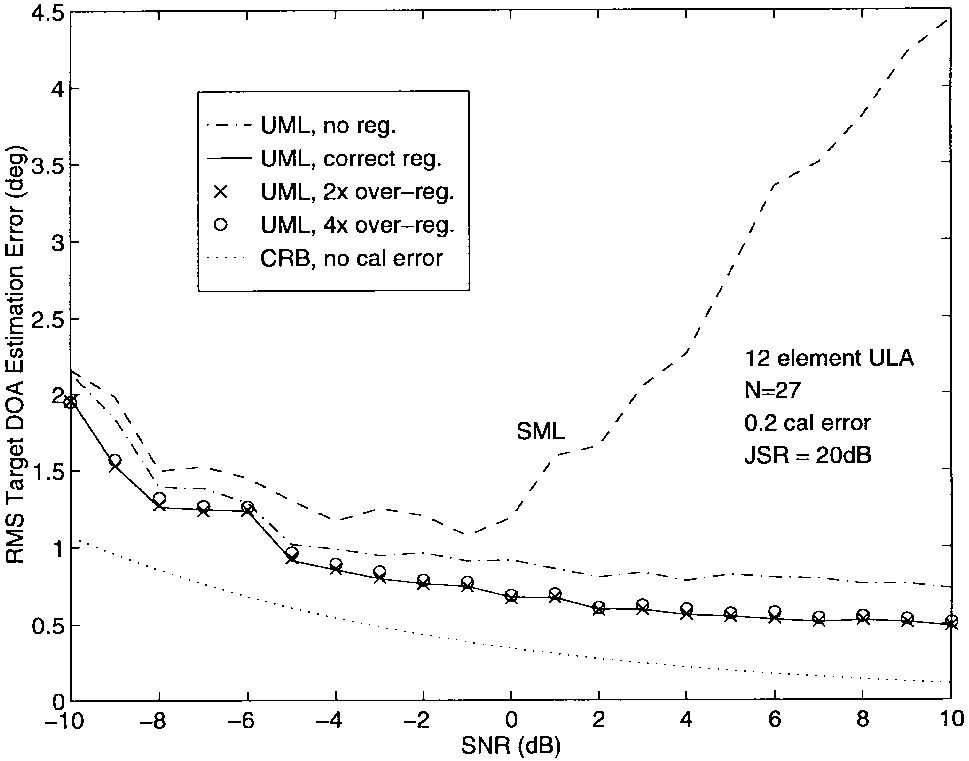
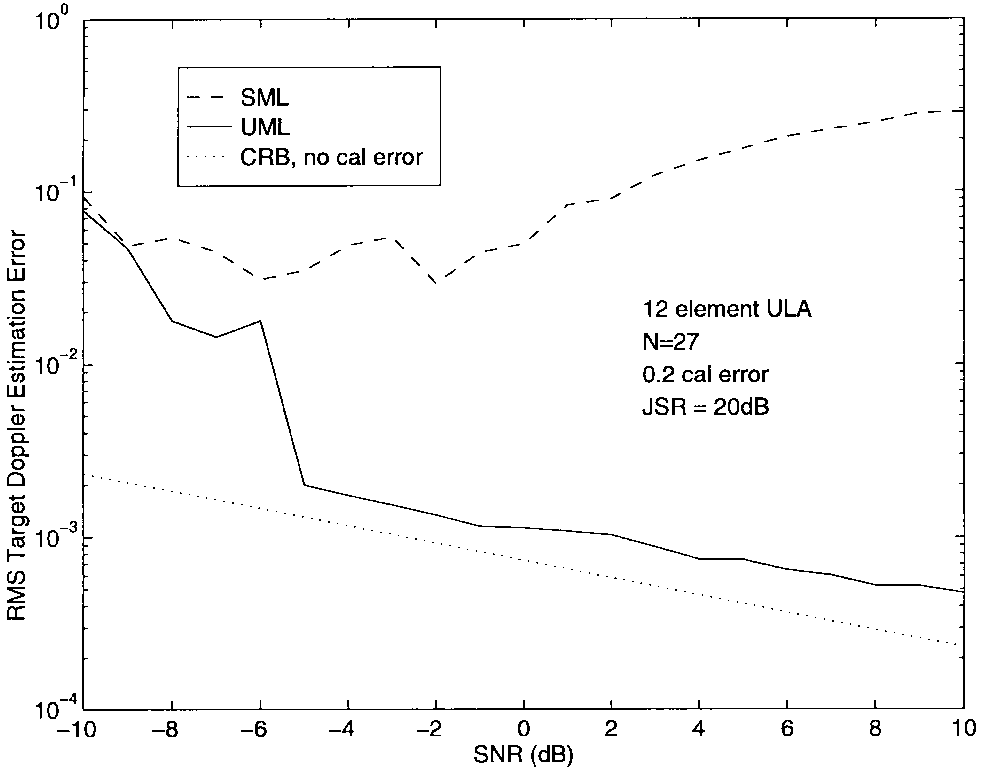
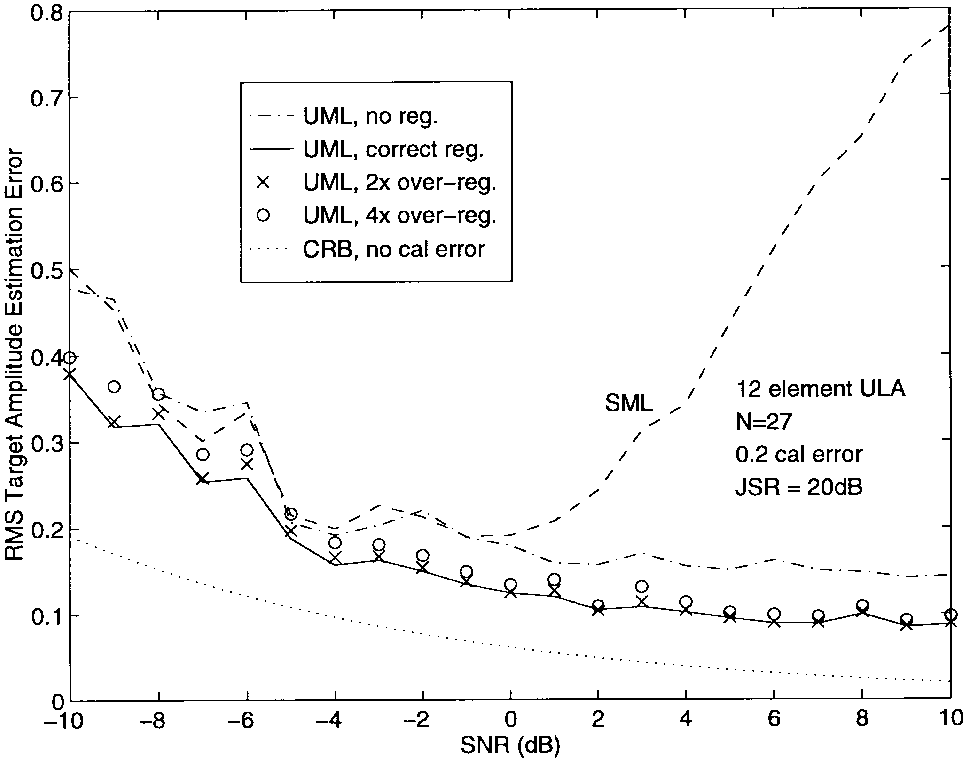
图10-12显示了当5°处存在干扰器且JSR = 20 dB时的结果。无论有无正则化，UML方法都比SML在高SNR时精确几倍。校准误差的存在降低了真实$\theta$和$\omega$处的2-D SML准则的峰值，并产生了远离它们的局部最大值。UML技术不会遇到这个问题，因为在高SNR时，它能够准确估计$\omega$而不受阵列扰动的影响。有了$\omega$的准确估计，DOA参数的误差相应减少。

结论

本文提出了几种用于雷达问题中检测和估计的技术，其中目标被具有未知空间协方差的噪声中的天线阵列观测。引入了两种数据模型：一种使用结构化模型，将目标信号幅度和DOA作为参数，另一种是阵列响应的更简单的非结构化模型。为每种情况推导了ML解并建立了相应的CRB。使用EXIP展示了如何处理更简单的非结构化解以估计具有与更复杂的结构化算法相同渐近精度的目标参数。

观察到EXIP方法的几个优点。首先，可以使用两个1-D搜索而不是一个2-D搜索获得目标参数的统计有效估计。由于估计通常通过在网格上评估给定准则来确定，这可以提供大量的计算节省。此外，如果使用均匀线性阵列，可以消除其中一个1-D搜索以进一步减少计算负担。其次，使用非结构化模型的两步方法为在目标DOA估计中考虑阵列校准误差提供了一种简单有效的方法。由此产生的DOA估计可以显著更准确，对此类误差的敏感性大大降低。最后，使用阵列响应的非结构化模型允许开发不依赖于阵列校准数据的准确性或可用性的似然比检测测试，也不依赖于目标DOA的先验信息。因此，在这些信息不精确已知的情况下，该测试是鲁棒的。我们的仿真表明，当阵列完美校准时，使用更简单的两步算法而不是直接结构化方法几乎没有退化。当存在校准或指向误差时，更简单的算法提供了更好的性能。

总之，使用非结构化阵列模型与EXIP相结合为将ML方法应用于雷达信号处理问题提供了一个非常简单的程序。所提出的估计和检测算法的计算简单性和鲁棒性使它们值得在实际雷达应用中认真考虑。

附录

附录A：结构化ML估计器的性质

A. 一致性

首先建立结构化ML算法的一致性。首先，我们有：

$$\underset{N\to \infty }{\lim }\mathbf{y}(\omega )=\underset{N\to \infty }{\lim }\frac{1}{N}\sum _{t=1}^N\left[b_0\mathbf{a}({\theta }_0)e^{j({\omega }_0-\omega )t}+\mathbf{e}(t)e^{-j\omega t}\right]$$

$$=\underset{N\to \infty }{\lim }\frac{1}{N}\sum _{t=1}^N{b}_0\mathbf{a}({\theta }_0)e^{j({\omega }_0-\omega )t}+\underset{N\to \infty }{\lim }\frac{1}{N}\sum _{t=1}^N\mathbf{e}(t)e^{-j\omega t}$$

如果我们令$\delta (\omega )$表示Kronecker delta函数，第一项的极限简单地为$b_0\mathbf{a}({\theta }_0)\delta ({\omega }_0-\omega )$，因为：

$$\underset{N\to \infty }{\lim }\frac{1}{N}\sum _{t=1}^N{e}^{j({\omega }_0-\omega )t}=\{\begin{array}{ll}1& \text{如果 }\omega ={\omega }_0\\ 0& \text{否则}\end{array}$$

根据大数定律，第二项以概率1一致收敛到零，因为$\mathbf{e}(t)$是零均值的。因此：

$$\underset{N\to \infty }{\lim }\mathbf{y}(\omega )=\{\begin{array}{ll}{b}_0\mathbf{a}({\theta }_0)& \text{如果 }\omega ={\omega }_0\\ 0& \text{否则}\end{array}\text{w.p.1}$$

令$\hat{\mathbf{R}}={\lim }_{N\to \infty }\hat{\mathbf{R}}$，则在$(16)$中的ML准则渐近地由下式给出：

$$V_N(\theta ,\omega )=\frac{|b_0{|}^2|{\mathbf{a}}^{\ast }(\theta ){\mathbf{R}}^{-1}\mathbf{a}({\theta }_0){|}^2}{[1-|b_0{|}^2{\mathbf{a}}^{\ast }({\theta }_0){\mathbf{R}}^{-1}\mathbf{a}({\theta }_0)]{\mathbf{a}}^{\ast }(\theta ){\mathbf{R}}^{-1}\mathbf{a}(\theta )}$$

概率为1。在$\omega \ne {\omega }_0$时，极限ML准则为零。柯西-施瓦茨不等式可以用来获得极限ML准则的以下上界：

$$\underset{N\to \infty }{\lim }{V}_N(\theta ,{\omega }_0)=\frac{|b_0{|}^2|{\mathbf{a}}^{\ast }(\theta ){\mathbf{R}}^{-1}\mathbf{a}({\theta }_0){|}^2}{c{\mathbf{a}}^{\ast }(\theta ){\mathbf{R}}^{-1}\mathbf{a}(\theta )}\le \frac{|b_0{|}^2{\mathbf{a}}^{\ast }({\theta }_0){\mathbf{R}}^{-1}\mathbf{a}({\theta }_0)}{c}$$

其中$c=1-|b_0{|}^2{\mathbf{a}}^{\ast }({\theta }_0){\mathbf{R}}^{-1}\mathbf{a}({\theta }_0)$。当且仅当${\mathbf{R}}^{-1/2}\mathbf{a}(\theta )=\kappa {\mathbf{R}}^{-1/2}\mathbf{a}({\theta }_0)$时等式成立，这进而只有当$\mathbf{a}(\theta )=\kappa \mathbf{a}({\theta }_0)$时才可能，因为我们隐含地假设了一个"无歧义"的阵列。

虽然极限ML准则在真实参数值处具有全局最大值，但由于准则在$\omega$中的不连续性，建立一致性是复杂的。使用类似于文献中引理1和定理1的论证可以解决这个问题。已经证明，只要$V_N(\theta ,\omega )$可以写成两个分量$V_N^{(1)}(\theta ,\omega )$和$V_N^{(2)}(\theta ,\omega )$的和，满足以下条件，就可以实现一致性：

B. Cramér-Rao界

由于结构化ML估计是一致的，它们将是统计有效的，其渐近方差将由CRB给出。在结构化模型下，观测$\mathbf{x}(1),\cdots ,\mathbf{x}(N)$是独立的圆形高斯随机变量，均值为：

$$\mathcal{E}\{\mathbf{x}(t)\}=b_0\mathbf{a}({\theta }_0)e^{j{\omega }_{0}t}$$

和协方差$\mathbf{Q}$，其中为简洁起见我们省略了下标$0$。在这种情况下，$N$个观测的FIM的元素$(i,j)$可以表示为：

$$[{\mathbf{J}}_N{]}_{ij}=N\cdot \text{tr}\left\{{\mathbf{Q}}^{-1}\frac{\partial \mathbf{Q}}{\partial {\eta }_i}{\mathbf{Q}}^{-1}\frac{\partial \mathbf{Q}}{\partial {\eta }_j}\right\}+2\text{Re}\left\{\sum _{t=1}^N\frac{\partial {\mu }^{\ast }(t)}{\partial {\eta }_i}{\mathbf{Q}}^{-1}\frac{\partial \mu (t)}{\partial {\eta }_j}\right\}$$

由于$\mathbf{Q}$和$\{b,\theta ,\omega \}$依赖于$\mathbf{\eta }$的不同元素，很明显${\mathbf{J}}_N$将相对于信号和噪声参数是块对角的。特别地，$(103)$的第一项只对噪声块给出非零结果，而第二项只对信号块非零。由于我们只关心信号参数的CRB，我们只需要考虑第二项：

$${\mathbf{J}}_N^{(s)}=2\text{Re}\left\{\sum _{t,s=1}^N\frac{\partial {\mu }^{\ast }(t)}{\partial {\mathbf{\eta }}_s}{\mathbf{Q}}^{-1}\frac{\partial \mu (s)}{\partial {\mathbf{\eta }}_s^T}\right\}{e}^{j({\omega }_0-\omega )(s-t)}$$

所需的偏导数如下：

$$\frac{\partial \mu (t)}{\partial \text{Re}\{b\}}=\mathbf{a}(\theta )e^{j\omega t}$$

$$\frac{\partial \mu (t)}{\partial \text{Im}\{b\}}=j\mathbf{a}(\theta )e^{j\omega t}$$

$$\frac{\partial \mu (t)}{\partial \theta }=jb\dot{\mathbf{a}}(\theta )e^{j\omega t}$$

$$\frac{\partial \mu (t)}{\partial \omega }=jtb\mathbf{a}(\theta )e^{j\omega t}$$

其中$\dot{\mathbf{a}}(\theta )=\frac{\partial \mathbf{a}(\theta )}{\partial \theta }$。

将这些代入$(104)$得到CRB表达式。为了找到ML多普勒和DOA估计的方差，我们使用分块对称矩阵逆的以下公式：

$${\left[\begin{array}{cc}\mathbf{A}& {\mathbf{B}}^T\\ \mathbf{B}& \mathbf{C}\end{array}\right]}^{-1}=\left[\begin{array}{cc}(\mathbf{A}-{\mathbf{B}}^T{\mathbf{C}}^{-1}\mathbf{B}{)}^{-1}& -{\mathbf{A}}^{-1}{\mathbf{B}}^T\mathbf{D}\\ -{\mathbf{D}}^T\mathbf{B}{\mathbf{A}}^{-1}& \mathbf{D}\end{array}\right]$$

其中$\mathbf{D}=(\mathbf{C}-\mathbf{B}{\mathbf{A}}^{-1}{\mathbf{B}}^T{)}^{-1}$是${\mathbf{J}}_N^{-1}$的下$2\times 2$块。为方便起见，定义：

$${\mathbf{Q}}_r=\text{Re}\{\mathbf{Q}\}$$
$${\mathbf{Q}}_i=\text{Im}\{\mathbf{Q}\}$$
$${\mathbf{\alpha }}_r=\text{Re}\{b_0\mathbf{a}({\theta }_0)\}$$
$${\mathbf{\alpha }}_i=\text{Im}\{b_0\mathbf{a}({\theta }_0)\}$$
$${\delta }_N=[{\gamma }_N-{\beta }_N^2]{\mathbf{\alpha }}_0^{\ast }{\mathbf{Q}}^{-1}{\mathbf{\alpha }}_0$$

${\beta }_N$、${\gamma }_N$由$(21)$和$(22)$定义。

估计方差因此由下式给出：

$$\mathcal{E}\{({\hat{\theta }}_s-{\theta }_0{)}^2\}=\frac{{\mathbf{a}}^{\ast }{\mathbf{Q}}^{-1}\mathbf{a}}{2N|b{|}^2[({\mathbf{a}}^{\ast }{\mathbf{Q}}^{-1}\mathbf{a})({\dot{\mathbf{a}}}^{\ast }{\mathbf{Q}}^{-1}\dot{\mathbf{a}})-|{\mathbf{a}}^{\ast }{\mathbf{Q}}^{-1}\dot{\mathbf{a}}{|}^2]}$$

$$\mathcal{E}\{({\hat{\omega }}_s-{\omega }_0{)}^2\}=\frac{1}{2N|b{|}^2({\gamma }_N-{\beta }_N^2){\mathbf{a}}^{\ast }{\mathbf{Q}}^{-1}\mathbf{a}}\approx \frac{6}{N^3|b{|}^2{\mathbf{a}}^{\ast }{\mathbf{Q}}^{-1}\mathbf{a}}$$

附录B：非结构化ML估计器的性质

A. 一致性

非结构化ML算法的一致性以类似于结构化情况的方式建立。按照$(96)$–$(98)$，我们有：

$$\underset{N\to \infty }{\lim }\mathbf{y}(\omega )=\{\begin{array}{ll}{\mathbf{\alpha }}_0& \text{如果 }\omega ={\omega }_0\\ 0& \text{否则}\end{array}$$

因此：

$$\underset{N\to \infty }{\lim }{\mathbf{y}}^{\ast }(\omega ){\hat{\mathbf{R}}}^{-1}\mathbf{y}(\omega )=\{\begin{array}{ll}{\mathbf{\alpha }}_0^{\ast }{\mathbf{R}}^{-1}{\mathbf{\alpha }}_0& \text{如果 }\omega ={\omega }_0\\ 0& \text{否则}\end{array}$$

将准则分成两项：

$${\mathbf{y}}^{\ast }(\omega ){\hat{\mathbf{R}}}^{-1}\mathbf{y}(\omega )=\frac{1}{N^2}\sum _{t,s=1}^N{\mathbf{\alpha }}_0^{\ast }{\mathbf{R}}^{-1}{\mathbf{\alpha }}_0{e}^{-j({\omega }_0-\omega )(t-s)}+\frac{1}{N^2}\sum _{t,s=1}^N[{\mathbf{\alpha }}_0^{\ast }{\mathbf{R}}^{-1}\mathbf{e}(t)e^{-j\omega s}+{\mathbf{e}}^{\ast }(s){\mathbf{R}}^{-1}{\mathbf{\alpha }}_0{e}^{j\omega t}+{\mathbf{e}}^{\ast }(s){\mathbf{R}}^{-1}\mathbf{e}(t)]e^{-j\omega (t-s)}$$

我们再次有两个满足一致性条件的函数。因此，${\lim }_{N\to \infty }{\hat{\omega }}_u={\omega }_0$，此外：

$$\underset{N\to \infty }{\lim }{\hat{\mathbf{\alpha }}}_u=\underset{N\to \infty }{\lim }\mathbf{y}({\hat{\omega }}_u)={\mathbf{\alpha }}_0$$

${\hat{\mathbf{Q}}}_u$的一致性通过将${\hat{\mathbf{\alpha }}}_u,{\hat{\omega }}_u$代入$(25)$得到。

B. Cramér-Rao界

非结构化模型下的数据$\mathbf{x}(1),\cdots ,\mathbf{x}(N)$是独立的圆形高斯随机变量，均值为${\mu }_u(t)={\mathbf{\alpha }}_0{e}^{j{\omega }_{0}t}$和协方差$\mathbf{Q}$。与结构化情况一样，非结构化CRB相对于信号$\{{\mathbf{\alpha }}_r,{\mathbf{\alpha }}_i,\omega \}$和噪声$(\mathbf{Q})$参数是块对角的。FIM的计算与$(104)$完全相同，用$\tilde{\mathbf{\eta }}$替换$\mathbf{\eta }$，所需的偏导数由下式给出：

$$\frac{\partial \mu (t)}{\partial {\mathbf{\alpha }}_r}=\mathbf{I}{e}^{j\omega t}$$

$$\frac{\partial \mu (t)}{\partial {\mathbf{\alpha }}_i}=j\mathbf{I}{e}^{j\omega t}$$

$$\frac{\partial \mu (t)}{\partial \omega }=jt\mathbf{\alpha }{e}^{j\omega t}$$

将$(117)$–$(119)$代入$(104)$得到FIM表达式。可以通过求逆$(120)$获得CRB的显式表达式。为此，我们使用$(112)$和矩阵求逆引理。

附录C：定理4的证明

通过将一般EXIP结果应用于结构化和非结构化ML雷达目标参数估计器的准则来证明该定理。特别地，将定义一个满足$(7)$的函数$f$，该函数关联SML和UML参数，并将显示$(9)$的WLS最小化简化为$(47)$–$(50)$、$(53)$和$(54)$。因此，定理1表明分别由$(47)$、$(48)$、$(53)$和$(54)$获得的$b$和$\theta$的估计渐近地与结构化ML算法获得的估计一样准确，因此在统计上是有效的。

关联$D_{\eta }$和$D_{\tilde{\eta }}$元素的函数$f$由下式隐式定义：

$${\mathbf{Q}}_s=\mathbf{Q}$$
$${\omega }_s=\omega$$
$$\text{Re}\{b_0\mathbf{a}({\theta }_0)\}=\text{Re}\{\mathbf{\alpha }\}=\mathbf{A}(\theta )\left(\begin{array}{c}{b}_r\\ b_i\end{array}\right)$$
$$\text{Im}\{b_0\mathbf{a}({\theta }_0)\}=\text{Im}\{\mathbf{\alpha }\}$$

其中：

$$\mathbf{A}(\theta )=\left[\begin{array}{cc}\text{Re}\{\mathbf{a}(\theta )\}& -\text{Im}\{\mathbf{a}(\theta )\}\\ \text{Im}\{\mathbf{a}(\theta )\}& \text{Re}\{\mathbf{a}(\theta )\}\end{array}\right]$$

这些方程连同在附录A和B中建立的两个算法的一致性，满足定理1的条件$(7)$和$(8)$。

由于在这个问题中使用了ML准则，$(10)$中的最优加权被视为等于FIM，在这种情况下是针对非结构化模型评估的。在附录B中显示，非结构化模型的FIM相对于信号$\{{\mathbf{\alpha }}_r,{\mathbf{\alpha }}_i,\omega \}$和噪声参数是块对角的，因此$(9)$的准则将由两项组成，一项仅涉及$\omega$，另一项仅涉及$\mathbf{Q}$的元素。因此，这两项可以分别最小化。由于$\mathbf{Q}$的参数化在结构化和非结构化模型下相同，涉及$\mathbf{Q}$的项可以通过简单地设置${\hat{\mathbf{Q}}}_e={\hat{\mathbf{Q}}}_u$使其为零。这建立了$(47)$。

涉及$\tilde{\mathbf{\eta }}$的剩余项通过将$(129)$和$(130)$代入$(9)$找到：

J=[(α^urα^uiω^u)−(A(θ)00A(θ)00)(brbiω)]TWQ~[(α^urα^uiω^u)−(A(θ)00A(θ)00)(brbiω)]J = \\left[\\begin{pmatrix} \\hat{\\boldsymbol{\\alpha}}_{ur} \\\\ \\hat{\\boldsymbol{\\alpha}}_{ui} \\\\ \\hat{\\omega}_u \\end{pmatrix} – \\begin{pmatrix} \\mathbf{A}(\\theta) & 0 \\\\ 0 & \\mathbf{A}(\\theta) \\\\ 0 & 0 \\end{pmatrix}\\begin{pmatrix} b_r \\\\ b_i \\\\ \\omega \\end{pmatrix}\\right]^T \\mathbf{W}_{\\tilde{Q}} \\left[\\begin{pmatrix} \\hat{\\boldsymbol{\\alpha}}_{ur} \\\\ \\hat{\\boldsymbol{\\alpha}}_{ui} \\\\ \\hat{\\omega}_u \\end{pmatrix} – \\begin{pmatrix} \\mathbf{A}(\\theta) & 0 \\\\ 0 & \\mathbf{A}(\\theta) \\\\ 0 & 0 \\end{pmatrix}\\begin{pmatrix} b_r \\\\ b_i \\\\ \\omega \\end{pmatrix}\\right]J=​​α^ur​α^ui​ω^u​​​−​A(θ)00​0A(θ)0​​​br​bi​ω​​​TWQ~​​​​α^ur​α^ui​ω^u​​​−​A(θ)00​0A(θ)0​​​br​bi​ω​​​

其中加权由在$\widehat{\tilde{\mathbf{\eta }}}$处评估的FIM给出。如果我们关于$\omega$最小化$(131)$，简单的计算得出${\hat{\omega }}_e={\hat{\omega }}_u$，这也验证了$(48)$。${\hat{\omega }}_e={\hat{\omega }}_u$的事实也证明了$(131)$等于$(49)$。方程$(50)$通过将$(53)$代入$(50)$获得。因此，定理4中的所有陈述都得到验证，证明完成。