声明:本学习笔记使用基于TeXmacs的专业编辑工具和octave环境实现,理论推导非原创,只是笔记和移植!内容完全是前几年学习B站大神DR_CAN的相关视频课程做的笔记整理,我只是将学习过程使用格式化编辑工具做了笔记,并将源代码进行整理注释移植到了octave(语法和matlab基本通用)调试运行,并寻找了网上其它文章有水印的图片补充理解,如果相关作者认为侵权,我立马删除。
因为网站无法实现专业编辑工具呈现效果,部分内容不得不使用截图,不然格式会乱。
原视频链接:https://space.bilibili.com/230105574
MPC(Model Predictive Control)模型预测控制
背景知识:状态空间方程(State Space), 反馈控制器设计(Feedback Control)、观测器
定义 1. 最优控制(Optimal Control)
研究动机(Motivation):在约束条件(物理限制,如方向盘转动极限)下达到最优(综合最优分析,思辨Critical Thinking)的系统表现Get the best performace within certain limitation,
数学模型(Mathmatical Model):
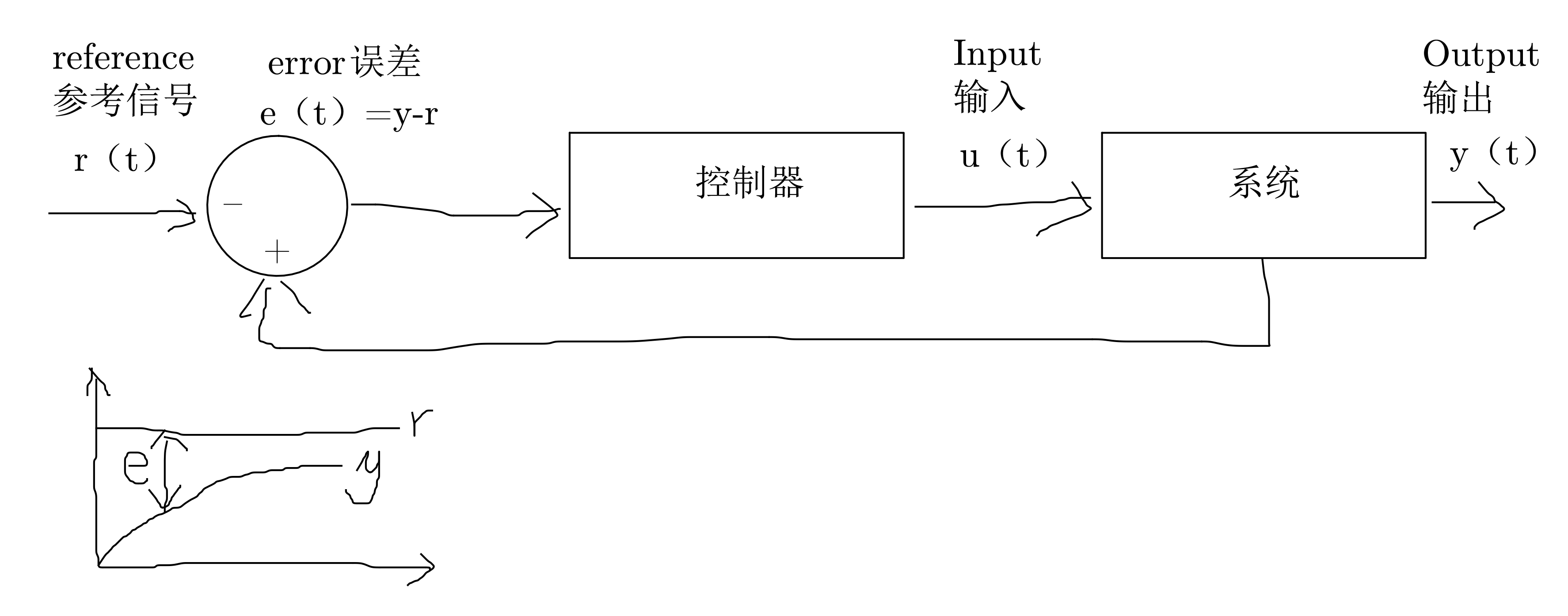
1.单输入单输出SISO(Single Input Single Output)
![]() ,引申学习泛函分析的内积空间
,引申学习泛函分析的内积空间
![]()

siso的状态空间方程类似于mimo,只是输入输出是1×1的标量,但状态向量的维度 n 可以大于1,因为系统内部可能包含多个相互关联的状态变量。
2.多输入多输出MIMO(Multiple Input Multiple Output)
![]()
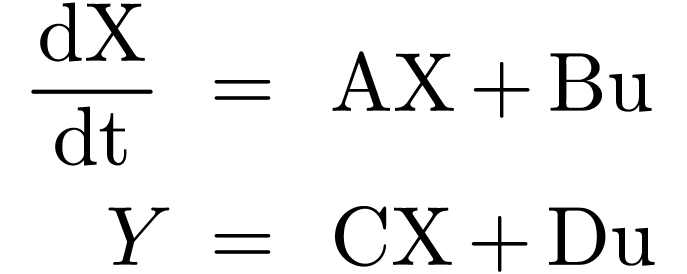
| 符号 | 名称 | 维度 | 作用 |
| A | 系统矩阵、状态矩阵、动态矩阵 | n×n | 描述系统状态变量之间关系 |
| B | 输入矩阵、控制矩阵 | n×p | 外部系统如何影响系统状态 |
| C | 输出矩阵、观测矩阵 | m×n | 系统状态如何影响输出 |
| D | 直接传递矩阵 | m×p | 表示输入如何直接作用于输出,可能为0 |
| X | 系统状态向量 | n×1 | 包含了足以完全表征系统运动状态的最小个数变量 |
| Y | 系统输出向量 | m×1 | 系统在t时刻输出 |
| u | 输入向量 | p×1 | 作用于系统上的外部输入或控制信号 |
A:系统矩阵、状态矩阵,描述系统状态变量之间关系
B:输入矩阵、控制矩阵,外部系统如何影响系统状态
C:输出矩阵、观测矩阵,系统状态如何影响输出
D:直接传递矩阵,表示输入如何直接作用于输出,可能为0
X:系统状态向量,包含了足以完全表征系统运动状态的最小个数变量
Y:系统输出向量,系统在t时刻输出
u:输入矩阵
代价函数(Q、R是调节权重系数的对角矩阵):
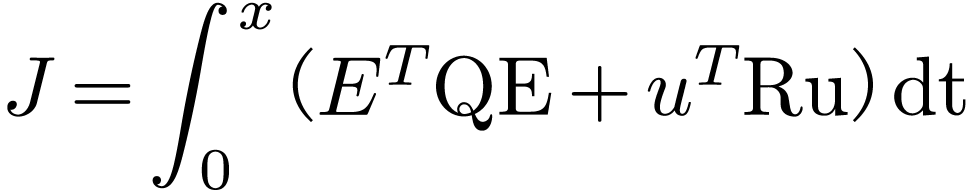
以二维系统为例:
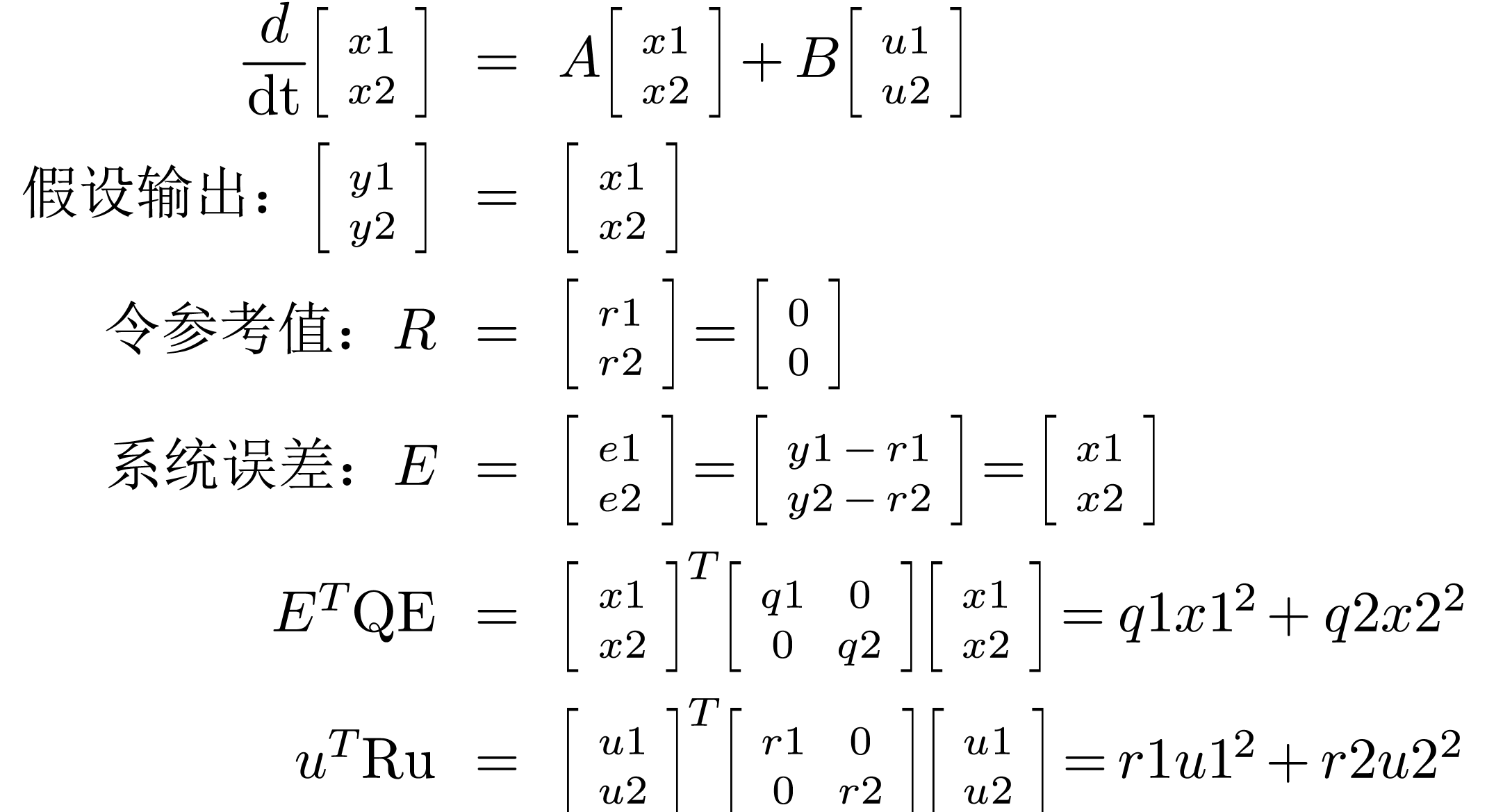
q1、q2、r1、r2:最优化系统的权重系数
定义 2. MPC基本概念(concept)
通过模型来预测系统在某一未来时间段内的表现来进行优化控制,因为多用于数位控制,所以采用离散型状态空间表达
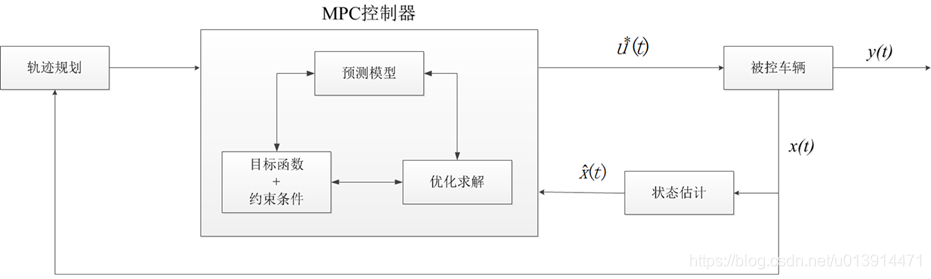

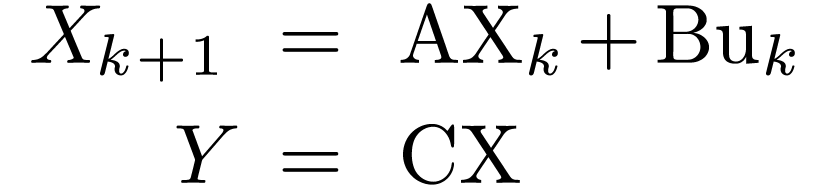
代价函数(离散型用加和,Q、R、F是调节权重系数的对角矩阵,F矩阵涉及求解李亚普诺夫函数,为了保证系统稳定性,待扩展学习):
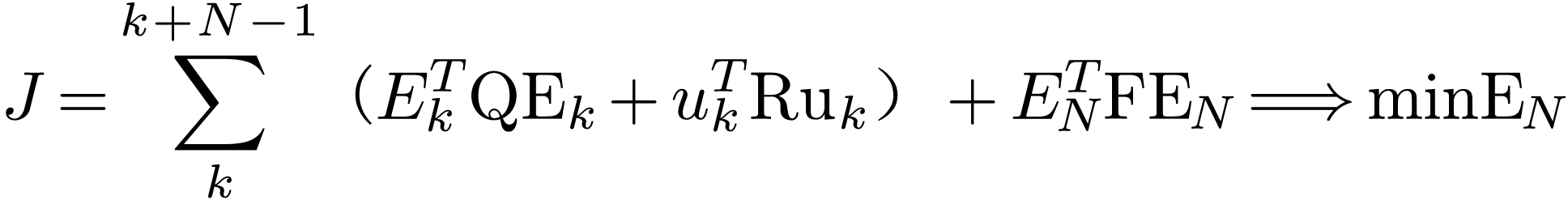
![]() :预测区间最终N时刻误差代价函数,过程最优+终值最优
:预测区间最终N时刻误差代价函数,过程最优+终值最优
还需要考虑系统约束(Constrains)
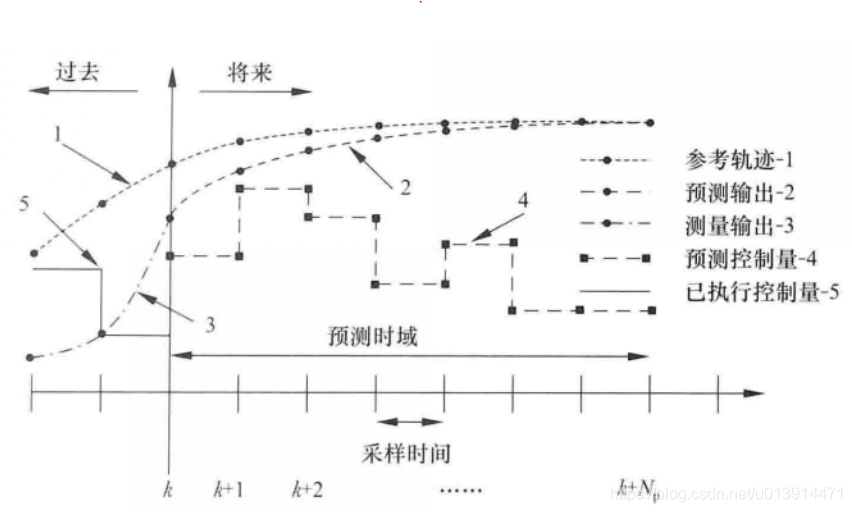
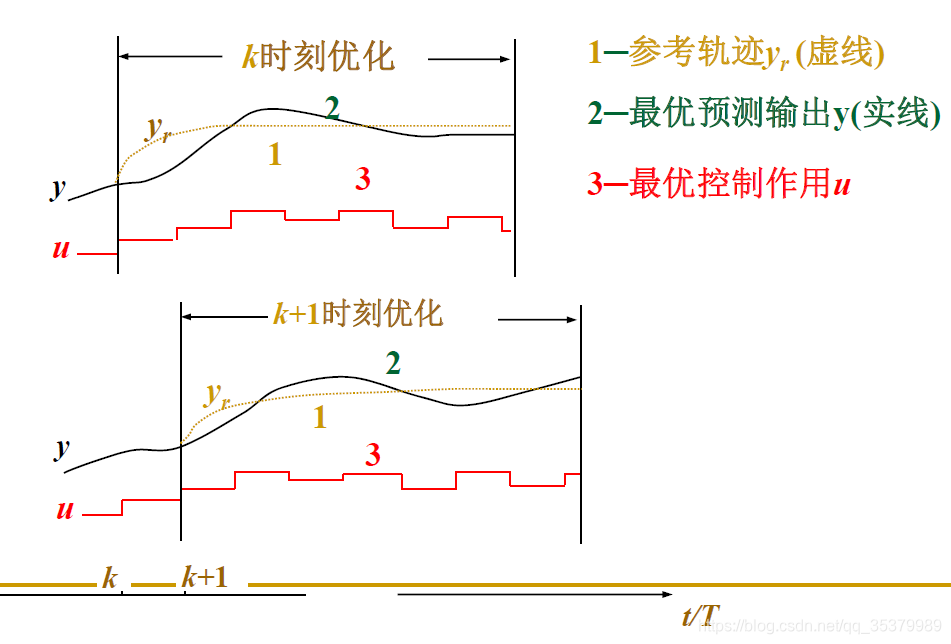
工作步骤分3步:
step 1:在k时刻,估计(有些无法直接测量,设计观测器)/测量读取当前系统状态
step 2:在k时刻,基于![]() ,
,![]() 来进行最优化控制(二次规划)
来进行最优化控制(二次规划)
step 3:滚动优化(Horizon Control),在k时刻只取![]() ,对抗扰动和实际环境误差,看N步走1步,后续取点越多只为保证k时刻值越优,每一步都要进行最优化求解,所以对硬件性能要求高
,对抗扰动和实际环境误差,看N步走1步,后续取点越多只为保证k时刻值越优,每一步都要进行最优化求解,所以对硬件性能要求高
定义 3. 二次规划(Quadratic Programing)


加权最小二乘法(Weighted Least Squares, WLS)是一种数学优化技术,它在普通最小二乘法(Least Squares, LS)的基础上引入了权重,以调整不同样本误差对损失函数的贡献率。这种方法在数据存在异方差性(即误差项的方差不同)时特别有用,可以通过加权使得模型更加准确地反映数据的实际特性。
加权最小二乘法主要适用于线性模型或可以转化为线性模型的非线性模型。对于某些复杂的非线性模型,可能需要采用其他优化方法。
对于MPC,需要把模型转化成一般形式,然后使用工具求解。
最小二乘求解工具:matlab,python
推论 4. MPC转二次规划求解推导

N:预测区间(Predictive Horizon)
为了简化推导,假设输出Y=X,参考R=0,E=Y-R=X-0=X
代价函数(离散型用加和,Q、R、F是调节权重系数的对角矩阵,逐项对应x和u的向量中每一项权重系数):

前半部分是误差加权和,后半部分是输入加权和
![]() 在预测区间终端的误差
在预测区间终端的误差
现在有x和u两个变量,但是二次型求解只有一个变量,控制器需要的是控制量u,需要把x转化成u
根据状态空间方程:

整理可得(下面的0指0矩阵):

其中![]()
![]() ,也是一个多状态向量
,也是一个多状态向量

Tips:
矩阵的转置分配律可以表述为:
(A+B)的转置等于A的转置与B的转置的和,即:(A + B)^T = A^T + B^T
矩阵的转置的转置等于原矩阵,即:(AT)T = A。
矩阵与其转置的乘积是一个对称矩阵,即:A^T * A 的结果是一个对称矩阵(当A为方阵时)。
矩阵乘积的转置满足(AB)^T = B^T * A^T,这个性质在处理矩阵乘法时非常有用。
(ABC)^T =C^T * B^T * A^T
例 5. 单输入二阶系统

假设N=3

%% 清屏
clear all; %释放内存,不受之前定义的变量或函数影响
close all; %关闭当前打开的所有图形窗口
clc; %清理命令窗口,以便查看最新的命令输出或结果
%% 加载 optim package,若使用matlab,则注释掉此行
pkg load optim;

function [E , H]=MPC_Matrices(A,B,Q,R,F,N)
n=size(A,1); % A 是 n × n 矩阵, 得到行数 n
disp(n);
p=size(B,2); % B 是 n × p 矩阵, 得到列数 p
disp(p);
% 定义M 和 C
M=[eye(n);zeros(N*n,n)]; % 初始化 M 矩阵. M 矩阵是 (N+1)n × n的,
% 上面是 n × n 个 "I"单位矩阵
% 下面是 N*n × n 的零矩阵,上下行堆叠
disp(M);
C=zeros((N+1)*n,N*p); % 初始化 C 矩阵, 这一步令它有 (N+1)n x NP 个 0
disp(C);
% 更新M和C
tmp=eye(n); %定义一个n x n 的 I 单位矩阵
disp(tmp);
for i=1:N % 循环,i 从 1到 N
rows =i*n+(1:n); %定义当前行数,从i x n开始,共n行
C(rows,:)=[tmp*B,C(rows-n, 1:end-p)]; %将c矩阵填满
tmp= A*tmp; %每一次将tmp左乘一次A
M(rows,:)=tmp; %将M矩阵写满
end
disp(M);
disp(C);
% 定义Q_bar和R_bar
% 克罗内克积是张量积的特殊形式,
% 如果A是m×n的矩阵,而B是p×q的矩阵,克罗内克积则是mp×nq的分块矩阵
Q_bar = kron(eye(N),Q);
disp(Q_bar);
% 创建分块对角矩阵,即主对角线上由多个子矩阵组成,而其余位置都是零的矩阵
Q_bar = blkdiag(Q_bar,F);
disp(Q_bar);
R_bar = kron(eye(N),R);
disp(R_bar);
% 计算G, E, H
% G: n x n
G=M'*Q_bar*M;
disp(G);
% E: NP x n
E=C'*Q_bar*M;
disp(E);
% NP x NP
H=C'*Q_bar*C+R_bar;
disp(H);
end
quadprog
二次规划,quadprog 仅适用于基于求解器的方法。
x = quadprog(H,f) 返回使 1/2*x'*H*x + f'*x 最小的向量 x。要使问题具有有限最小值,输入 H 必须为正定矩阵。如果 H 是正定矩阵,则解 x = H\\(-f)。
function u_k= Prediction(x_k,E,H,N,p)
U_k = zeros(N*p,1); % NP x 1
U_k = quadprog(H,E*x_k); %求解二次规划问题
u_k = U_k(1:p,1); % 取第一个结果
end
假设:

%% 第一步,定义状态空间矩阵
%% 定义状态矩阵 A, n x n 矩阵
A = [1 0.1; -1 2];
n= size (A,1); %获取矩阵A的第一维的大小,即矩阵A的行数
disp(A);
disp(n);
%% 定义输入矩阵 B, n x p 矩阵
B = [ 0.2 1; 0.5 2];
p = size(B,2); %获取矩阵B的第二维的大小,即矩阵B的列数
disp(B);
disp(p);
%% 定义Q矩阵,n x n 矩阵,x1和x2的权重
Q=[100 0;0 1];
disp(Q);
%% 定义F矩阵,n x n 矩阵,终项x1和x2的权重
F=[100 0;0 1];
disp(F);
%% 定义R矩阵,p x p 矩阵,u1和u2的消耗权重
R=[1 0 ;0 .1];
disp(R);
%% 定义step数量k,预测100次
k_steps=100;
%% 定义矩阵 X_K, n x k 矩 阵
X_K = zeros(n,k_steps); % 创建一个n * k_steps的全零矩阵
disp(X_K);
%% 每一列都是某一时刻的系统状态
%% 初始状态变量值, n x 1 向量
X_K(:,1) =[20;-20]; % 对所有行的第1列赋值向量
disp(X_K);
%% 定义输入矩阵 U_K, p x k 矩阵
U_K=zeros(p,k_steps); % 创建一个p * k_steps的全零矩阵
disp(U_K);
%% 定义预测区间K
N=5;
%% Call MPC_Matrices 函数 求得 E,H矩阵
[E,H]=MPC_Matrices(A,B,Q,R,F,N);
disp([E,H]);
%% 计算每一步的状态变量的值,把100次的输入输出记下来准备绘图
for k = 1 : k_steps
%% 求得U_K(:,k),得到每个预测的第一个输入,写到k列
U_K(:,k) = Prediction(X_K(:,k),E,H,N,p);
%% 根据状态方程计算第k+1步时状态变量的值
X_K(:,k+1)=(A*X_K(:,k)+B*U_K(:,k));
end
disp(U_K);
disp(X_K);
%% 绘制状态变量和输入的变化
figure;
%subplot (2, 1, 1);
hold on; %启用保持当前图形状态,允许在同一坐标系上绘制新的图形。
for i =1 :size (X_K,1)
plot (X_K(i,:));
end
legend("x1","x2") %添加图例,以便区分图形中的不同数据系列
title('system state');
xlabel('k');
ylabel('X_K');
drawnow; % 强制更新图形
hold off; %关闭保持当前图形状态,接下来的绘图命令将清除当前图形并绘制新的图形。

figure;
%subplot (2, 1, 2);
hold on;
for i =1 : size (U_K,1)
plot (U_K(i,:));
end
legend("u1","u2");
title('system input');
xlabel('k');
ylabel('U_K');
drawnow; % 强制更新图形
hold off;

 网硕互联帮助中心
网硕互联帮助中心



评论前必须登录!
注册