大模型MoE架构深度解析

大模型MoE架构深度解析：从稀疏激活到系统协同的工程实现

引言：稀疏激活的本质与数学定义

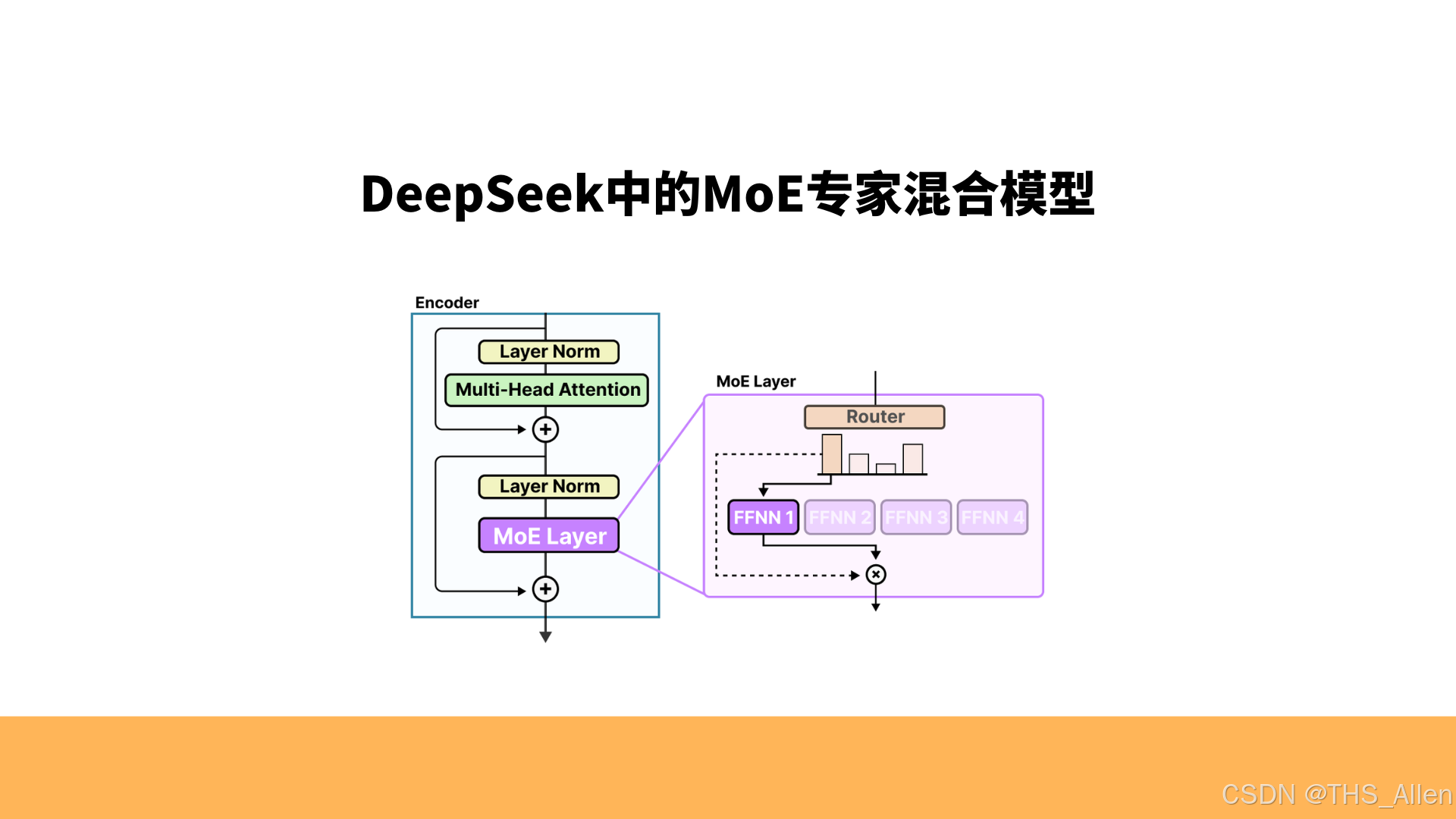
混合专家模型（Mixture-of-Experts, MoE）并非全新概念，但直至大模型时代，其“超大规模稀疏激活”的特性才真正释放出工程价值。MoE的核心矛盾在于：如何在维持计算开销基本不变的前提下，无限扩展模型参数量。其数学本质是一种条件计算范式——对于每个输入，仅激活模型总参数的一个极稀疏子集。

定义标准Transformer层为函数FFN(x)，MoE层则将其扩展为：

MoE(x) = ∑_{i=1}^N G(x)_i · E_i(x)

其中N为专家总数，E_i为第i个专家（通常为FFN），G(x)为门控网络的输出概率分布。计算瓶颈在于G(x)必须为稀疏向量，否则上式退化为参数倍增的密集模型。TopK稀疏化是工业界标准解法：

G(x) = Softmax(TopK(W_g · x, k))

TopK函数将非TopK位置的logits置为-∞，经Softmax后对应概率为0。这一定义直接决定MoE的计算效率：当N=64, k=2时，单次前向的计算量仅为密集模型的2/64=3.125%。

然而，这一定义的简洁性背后隐藏着三重深层挑战：路由决策的可学习性、专家负载的分布均衡、分布式系统的通信模式。本文将从门控网络的具体实现出发，逐层深入至系统级优化，完整呈现MoE的技术全貌。

一、门控网络与动态路由的实现粒度

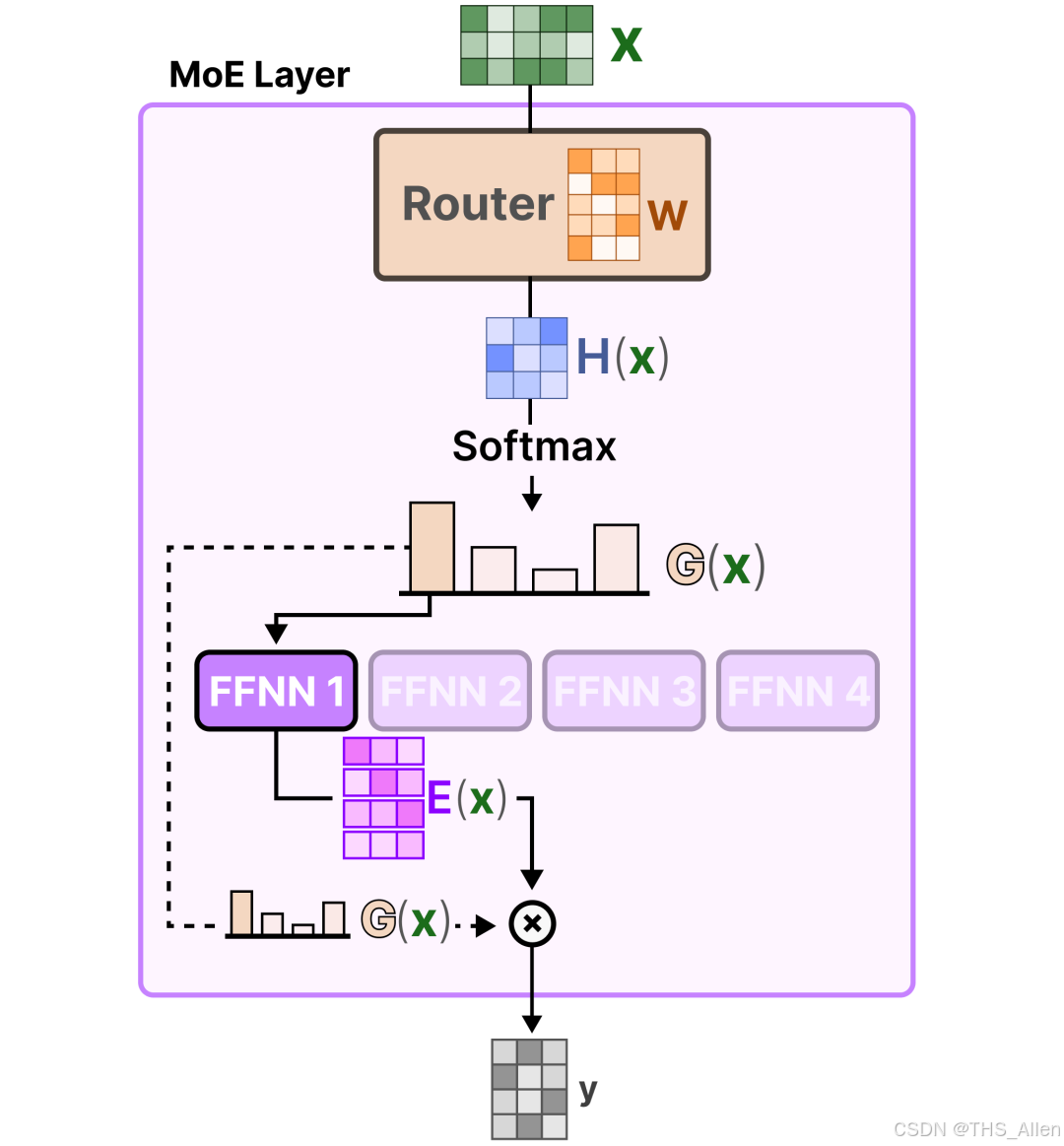
1.1 门控的数学形式与梯度传播

在代码层面，门控网络是一个独立的线性层，其输入为hidden_dim维向量，输出为num_experts维logits。以Qwen3-14B的MoE实现为例，其伪代码已给出标准范式：

class MoEGating(nn.Module):
def __init__(self, hidden_dim, num_experts, top_k=2):
super().__init__()
self.router = nn.Linear(hidden_dim, num_experts, bias=