从零开始用自定义 Triton 内核编写 FlashAttention-2

本文实现 FlashAttention-2 的前向传播，具体包括：为 Q、K、V 设计分块策略；流式处理 K 和 V 块而非物化完整注意力矩阵；实现在线 softmax 算法保证数值稳定性；支持因果和非因果两种注意力模式；用 Triton autotuner 自动调优内核配置；最后用 PyTorch 验证正确性。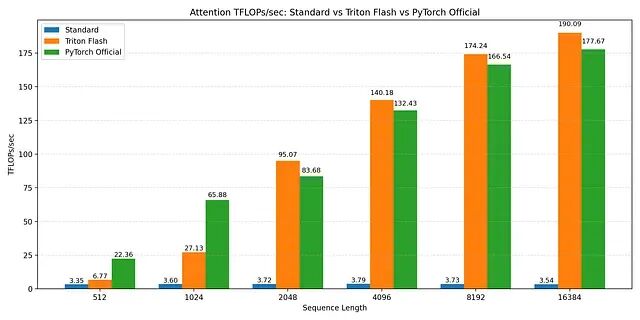

FlashAttention vs. standard attention vs torch2.2 (spda flashattn) TFLOP/s benchmarks

标准注意力为什么是内存受限的

标准注意力的瓶颈不在浮点运算量而在内存带宽。普通注意力计算 S = QKᵀ 之后，要把完整的 N × N 矩阵写入 HBM再读回来算 softmax 并存储然后再读一次乘以 V，每个元素被访问 2-4 次每次都走 HBM。

序列长度 16K 时，这个矩阵包含 16,384² ≈ 2.56 亿个元素。

反复在 HBM 和计算单元之间搬运这几亿个值，而HBM 是 GPU 上容量最大的内存也是最慢的。A100 上从 HBM 读数据比从片上 SRAM 读大约慢 15 倍。大张量和模型权重都放在这里，所以写内核的首要目标就是减少 HBM 流量把高频访问的数据留在寄存器或共享内存里。

核心方案——让注意力具备 IO 感知能力

FlashAttention 的核心思想是让注意力变得 IO 感知。所谓 IO 感知就是真正理解并利用一个这个定义：片上 SRAM 比 HBM 快几个数量级。NVIDIA A100 有 40-80GB HBM（也就是那个让你频繁遭遇 CUDA OOM 的全局内存）带宽 1.5-2.0 TB/s；每个 SM 有 192KB SRAM，共 108 个 SM，带宽估计 19TB/s 左右。

GPU 硬件有个黄金法则：

把数据搬到内存层次的上层然后留在那里。除非万不得已别回 HBM。

标准注意力完全无视这条规则，把 HBM 读写当成零成本操作。FlashAttention 计算的结果和标准缩放点积注意力完全一样：

S = QKᵀ ∈ ℝᴺˣᴺ，P = softmax(S) ∈ ℝᴺˣᴺ，O = PV ∈ ℝᴺˣᵈ

区别在于计算的调度方式。FlashAttention 不在 HBM 里存储那个巨大的 N × N 注意力矩阵然后再读回来算 softmax而是重新组织计算：分块处理序列从全局内存流式读取 K 和 V 块，用在线 softmax 增量计算每个块的部分结果，逐步构建输出矩阵 O反向传播时还可以选择重算而非存储。

具体操作是这样的：拿一块查询 Q_block，然后分块迭代 K 和 V 序列，边迭代边做在线 softmax 同时追踪必要的统计量，累积输出块并在片上归一化，只把最终结果写回 HBM。

这样注意力的内存复杂度就从 O(N²) 降到了 O(N)。

最难的部分——Softmax

分块矩阵乘法不难，而分块 softmax 才是麻烦事。注意力中 token i 对其他 token 的关注程度，是对该行所有注意力分数做 softmax 得到的：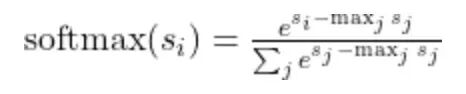

普通注意力里这很简单，因为一个 token 的全部注意力分数已经物化在内存中，一步就能算完最大值、归一化、softmax。

而FlashAttention 里情况不一样，键和值是分块流式进来的内核迭代 K 和 V 时只能看到部分分数块，永远看不到完整的分数集，就没法一步算完 softmax。

解决方案是在线 softmax 公式。不一步算完，而是维护三个逐查询的状态：运行最大值 mᵢ（保证数值稳定），运行归一化项 lᵢ，运行输出累加器 Oᵢ。每来一个新的注意力分数块，就更新这些值，最后恢复的结果和对整个序列做完整 softmax 一模一样。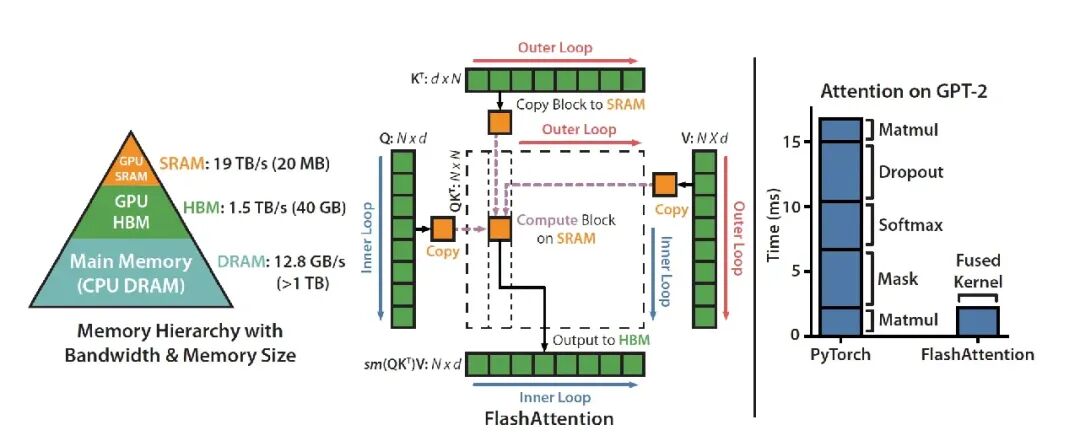

完整代码分解

从高层看，实现结构如下：

for each (batch, head):
for each Q_block:
initialize m_i, l_i, O_block
for each K/V block:
compute partial scores
update online softmax state
accumulate output
write O_block to memory

所有逻辑融合在内核里，中间状态全部驻留在片上快速内存。下面逐步讲解这个结构如何映射到 Triton 程序和 GPU 执行。

Host 包装器和内核启动

Python 包装器负责准备输入并启动 Triton 内核，做三件事：验证和提取输入张量的形状与步幅，构建内核执行网格，启动前向注意力内核。包装器本身不含注意力逻辑，只定义工作如何在 GPU 上调度。

# Host wrapper that prepares our inputs and parameters and runs the triton kernel
class TritonFlashAttention(torch.autograd.Function):
@staticmethod
def flash_attention(Q, K, V, causal):
assert Q.is_cuda
assert K.is_cuda
assert V.is_cuda

B, H, Lq, D = Q.shape
B, H, Lk, D = K.shape
B, H, Lk, D = V.shape

# create the output buffer
O = torch.empty_like(Q)

# we set block_sizes manually for now. We will autotune this later
[#BLOCK](#BLOCK)_SIZE_Q = 128
[#BLOCK](#BLOCK)_SIZE_KV = 32

stage = 3 if causal else 1

grid = lambda x: (triton.cdiv(Lq, x["BLOCK_SIZE_Q"]),
B * H, 1)
M = torch.empty((B, H, Lq), device=Q.device, dtype=torch.float32)

scaling_factor = 1 / math.sqrt(D)
fwd_flash_attn_kernel[grid](Q, K, V, O, M, scaling_factor,
Q.stride(0), Q.stride(1), Q.stride(2), Q.stride(3),
K.stride(0), K.stride(1), K.stride(2), K.stride(3),
V.stride(0), V.stride(1), V.stride(2), V.stride(3),
O.stride(0), O.stride(1), O.stride(2), O.stride(3),
B, NUM_HEADS=H, SEQ_LEN=Lq, HEAD_DIM=D, STAGE=stage,)
[#ctx](#ctx).save_for_backward

return O

程序网格和并行化策略

host 包装器里定义了一个 2D 执行网格，决定 GPU 如何分配工作，也就是并行启动多少个 Triton 程序实例。

grid=lambdax: (triton.cdiv(Lq, x["BLOCK_SIZE_Q"]), B*H, 1)

第一维 program_id(0) 标识程序实例处理的查询序列块，第二维 program_id(1) 标识对应的 (batch, head) 对。

维度 0 把查询序列分成 BLOCK_SIZE_Q 大小的块，Lq 是查询序列长度，每个程序实例负责计算输出矩阵的一个水平"条带"。维度 1 跨所有 batch 和 head 并行，每个程序实例对应一个 (batch, head) 对。给每个注意力头分配独立程序可以最大化占用率。内核内部用 tl.program_id 配合手动步幅算术（qb_stride、qh_stride）把每个 worker 指向它的内存切片。

每个程序实例负责计算：

Q[batch, head, q_block : q_block+BLOCK_SIZE_Q]

这种网格设计提供了序列维度并行、batch 和 head 并行，而且程序间不需要同步。每个程序在紧凑独立的工作集上运行，tl.program_id 结合显式步幅算术把每个实例映射到对应内存切片。

内核分解

前向传播分成两个内核。fwd_flash_attn_kernel 协调执行，加载查询块、处理因果逻辑、写输出。_attn_fwd_inner 实现核心 FlashAttention-2 计算，流式处理 K/V 块并执行在线 softmax 更新。每个 Triton 程序实例计算一个查询块 × 一个注意力头 × 一个 batch 元素。

这种分解把控制逻辑和流式计算分开内核更容易理解和优化。

前向内核

这个内核本身不直接实现注意力算法，负责的是把 GPU 程序实例映射到输入张量的对应块，协调流式注意力计算，处理因果逻辑，把最终输出写回内存。

@triton.jit
def fwd_flash_attn_kernel(q_ptr, k_ptr, v_ptr, o_ptr, m_ptr, scale,
qb_stride, qh_stride, qn_stride, qd_stride,
kb_stride, kh_stride, kn_stride, kd_stride,
vb_stride, vh_stride, vn_stride, vd_stride,
ob_stride, oh_stride, on_stride, od_stride,
BATCH_SIZE, NUM_HEADS:tl.constexpr, SEQ_LEN:tl.constexpr, HEAD_DIM:tl.constexpr,
BLOCK_SIZE_Q:tl.constexpr, BLOCK_SIZE_KV:tl.constexpr, STAGE:tl.constexpr):

# get the id of this program instance
block_index_q = tl.program_id(0) # Which chunk of sequence this program is responsible for
index_batch_head = tl.program_id(1) # what batch-head to process. zooms out

# get exact batch
index_batch = index_batch_head // NUM_HEADS

# get exact head
index_head = index_batch_head % NUM_HEADS

# create offsets to get the index of sequences we are going to process
qkv_offset = index_batch * qb_stride + index_head * qh_stride # i.e move from the first to the correct batch then move to the correct head within that batch
qkv_offset_K = index_batch * kb_stride + index_head * kh_stride
qkv_offset_V = index_batch * vb_stride + index_head * vh_stride
qkv_offset_O = index_batch * ob_stride + index_head * oh_stride

off_q = block_index_q * BLOCK_SIZE_Q + tl.arange(0, BLOCK_SIZE_Q) # same as off_q (in this head what q block do we need to read )
off_kv = tl.arange(0, BLOCK_SIZE_KV)
off_head = tl.arange(0, HEAD_DIM)

# create blocks of pointers to get the address of where the index lives
Q_block_ptr = q_ptr + qkv_offset + off_q[:, None] * qn_stride + off_head[None, :] * qd_stride
O_block_ptr = o_ptr + qkv_offset_O + off_q[:, None] * on_stride + off_head[None, :] * od_stride

m_i = tl.zeros((BLOCK_SIZE_Q,), dtype= tl.float32) – float("inf")

l_i = tl.zeros((BLOCK_SIZE_Q,), dtype=tl.float32) + 1.0
O_block = tl.zeros((BLOCK_SIZE_Q, HEAD_DIM), dtype=tl.float32)
Q_block = tl.load(Q_block_ptr) # add a mask

# stage 1: Blocks before the diagonal
# stage 2: diagonal block itself
# stage 3: for non-causal no masking is needed. For causal mask all the blocks here.

# runs if causal is True i.e we mask out the future tokens from contributing
# this if statement executes for non-causal attention (no masking) or for the blocks to the left of the diagonal in the causal attention
# Stage = 3 if causal else 1
if STAGE == 1 or STAGE == 3:
O_block, l_i, m_i = _attn_fwd_inner(
O_block,
l_i,
m_i,
Q_block,
block_index_q,
scale,
BLOCK_SIZE_Q,
BLOCK_SIZE_KV,
4 – STAGE,
off_kv,
off_q,
off_head,
kn_stride,
kd_stride,
vd_stride,
vn_stride,
k_ptr,
v_ptr,
qkv_offset_K,
qkv_offset_V,
SEQ_LEN,
HEAD_DIM
)

# this executes for blocks to the right of the diagonal in the causal attention
if STAGE == 3:
O_block, l_i, m_i = _attn_fwd_inner(
O_block,
l_i,
m_i,
Q_block,
block_index_q,
scale,
BLOCK_SIZE_Q,
BLOCK_SIZE_KV,
2,
off_kv,
off_q,
off_head,
kn_stride,
kd_stride,
vd_stride,
vn_stride,
k_ptr,
v_ptr,
qkv_offset_K,
qkv_offset_V,
SEQ_LEN,
HEAD_DIM
)

m_i += tl.math.log(l_i)
O_block = O_block / l_i[:, None]
m_ptrs = m_ptr + index_batch_head * SEQ_LEN + off_q
tl.store(m_ptrs, m_i)
tl.store(O_block_ptr, O_block.to(tl.float16))

网格映射

回顾 Python 包装器里的网格：

grid = (
ceil_div(Lq, BLOCK_SIZE_Q),
B * H
)

这个 2D 网格映射提供序列维度并行和 batch/head 并行。

内核内部：

block_index_q =tl.program_id(0)
index_batch_head =tl.program_id(1)

解码第二维：

index_batch=index_batch_head//NUM_HEADS
index_head =index_batch_head%NUM_HEADS

这几个变量唯一标识当前程序实例负责哪个 batch 元素、哪个注意力头、哪个查询块。

指针算术和张量布局

PyTorch 或 numpy 里用多维语法索引张量，比如 Q[batch, head, seq_pos, dim]。而Triton 内核里没有多维张量，只有指向输入第一个元素的裸指针 q_ptr必须用指针算术手动重构索引。

查询张量 Q 形状是 [BATCH, HEADS, SEQ_LEN, HEAD_DIM]，硬件层面是扁平一维数组存储。沿每个维度移动用步幅：qb_stride 跳一个 batch，qh_stride 跳一个 head，qn_stride 跳一个 token，qd_stride 跳一个特征。

选择 batch 和 head

每个程序实例先选定自己负责的 batch 和 head 切片：

qkv_offset=index_batch*qb_stride+index_head*qh_stride

这个偏移之后，指针指向 Q[batch, head, 0, :]。K、V、O 同理，用各自的步幅。然后构建当前块的索引范围：

off_q =block_index_q*BLOCK_SIZE_Q+tl.arange(0, BLOCK_SIZE_Q)
off_head=tl.arange(0, HEAD_DIM)

用这些偏移加广播，构建指向查询块的指针：

Q_block_ptr=q_ptr+qkv_offset \\
+off_q[:, None] *qn_stride \\
+off_head[None, :] *qd_stride

输出 O_block_ptr 也类似：

O_block_ptr=o_ptr+qkv_offset_O \\
+off_q[:, None] *on_stride \\
+off_head[None, :] *od_stride

完全用指针算术重现了 4D 索引 Q[batch, head, q_positions, head_dim]。

这种显式指针构建很关键，确保只加载每个程序实例需要的 Q 块并送到 SRAM，避免碰不相关的内存，实现合并访问，最大化缓存复用。

初始化每块状态

加载查询块后，内核初始化在线 softmax 所需的每块状态并分派流式计算。流式逻辑和因果阶段的细节在 _attn_fwd_inner 里，后面分析。先理解这个每块状态为什么存在、代表什么。

为了在迭代 K 和 V 块时正确增量计算 softmax，需要追踪三个量：运行最大值 m_i、运行 softmax 分母 l_i、未归一化加权和 O_block。

这三个变量构成在线 softmax 算法的状态。FlashAttention 分块处理键值，内核永远无法一次访问所有注意力分数。要得到和完整 softmax 一样的结果，必须维护数值稳定用的运行最大值 m_i、运行归一化因子 l_i、累积加权输出 O_block。这些状态共同作用，精确重建 softmax(QKᵀ) @ V，不需要物化注意力矩阵。

运行最大值 m_i 和运行归一化器

Softmax 涉及指数运算，FP16/BF16 下容易数值不稳定。为了把指数保持在合理范围，每个查询行追踪一个运行最大值 m_i。处理新的 K 和 V 块时，这个运行最大值可能增大。一旦增大，之前用旧最大值计算的累积贡献就不在同一尺度上了。

纠正办法是用一个因子重新缩放累积的分母：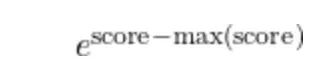

the numerator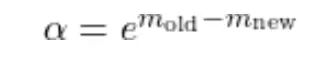

the scaling factor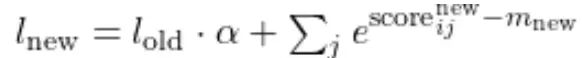

the normalizing denominator

这种重新缩放确保分母里所有项都相对同一个最大值。流式处理键值块时反复应用这个更新就能恢复精确的 softmax 归一化因子，不需要物化完整的注意力分数集。

内核里是这样写：

alpha=exp(m_old-m_new)
l_i=l_i*alpha+l_ij

累积输出 O_block

注意力输出定义为：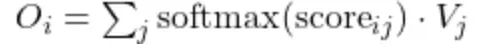

Final attention output

标准实现里可以直接算，因为完整的 softmax 归一化系数事先就知道。FlashAttention 里键值分块流式进来，最终归一化因子要等所有 K 和 V 块处理完才能确定。

所以只能累积一个未归一化的加权和，最后再归一化。

每次迭代，计算相对于当前运行最大值的块级 softmax 概率：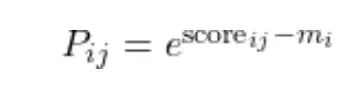

维护一个未归一化输出累加器：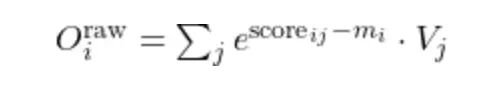

unnormalized softmax output

处理新 K/V 块时运行最大值可能变，之前累积的输出必须重新缩放以匹配新最大值。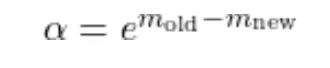

逐块更新输出累加器：

O_block=O_block*alpha[:, None]
O_block=P_block@V_block+O_block

所有 K/V 块处理完后，把累积的未归一化输出除以累积的 softmax 分母 li 得到最终注意力输出：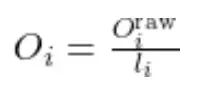

final normalization

结果和标准 softmax 注意力完全一样，但永远不会在内存里物化完整注意力矩阵或 softmax 概率。

每个程序实例为每个查询块初始化这三个状态一次：

m_i=tl.zeros((BLOCK_SIZE_Q,), dtype=tl.float32) -inf
l_i=tl.zeros((BLOCK_SIZE_Q,), dtype=tl.float32) +1
O_block=tl.zeros((BLOCK_SIZE_Q, HEAD_DIM), dtype=tl.float32)

流式注意力内核 _attn_fwd_inner

_attn_fwd_inner 实现 FlashAttention-2 算法核心，由 fwd_flash_attn_kernel 调用，一次处理一个查询块。

@triton.jit
def _attn_fwd_inner(O_block, l_i,m_i, Q_block, block_index_q,
scale: tl.constexpr,
BLOCK_SIZE_Q: tl.constexpr,
BLOCK_SIZE_KV: tl.constexpr,
STAGE: tl.constexpr,
off_kv: tl.constexpr,
off_q: tl.constexpr,
off_head: tl.constexpr,
kn_stride: tl.constexpr,
kd_stride: tl.constexpr,
vd_stride: tl.constexpr,
vn_stride: tl.constexpr,
k_ptr,
v_ptr,
qkv_offset_K: tl.constexpr,
qkv_offset_V: tl.constexpr,
SEQ_LEN:tl.constexpr,
HEAD_DIM: tl.constexpr):

其中 Q_block 形状 [BLOCK_SIZE_Q, HEAD_DIM]，O_block 是累积输出，m_i 是每查询行的运行最大值，l_i 是运行 softmax 归一化。

因果块范围选择

FA 内核支持因果（只看过去和当前 token）和非因果注意力（双向，可以看未来）。用一个阶段机制实现：

if STAGE == 1:
lo, hi = 0, block_index_q * BLOCK_SIZE_Q
elif STAGE == 2:
lo, hi = block_index_q * BLOCK_SIZE_Q, (block_index_q + 1) * BLOCK_SIZE_Q
else:
lo, hi = 0, SEQ_LEN

这个逻辑决定当前内核处理哪些 K/V 块。Stage 1 是对角线左侧的块，K 和 V 范围仅限于此。Stage 2 是对角线块本身。Stage 3 是非因果逻辑，K 和 V 关注所有 Q。这样避免计算因果注意力中肯定会被 mask 掉的分数，减少不必要的 masking 工作。

K 和 V 块的流式循环

查询虽然分区到各程序实例，但每个查询块必须关注所有键值——这是全注意力的定义决定的。完整 K 和 V 矩阵从不一次性加载到 SRAM，而是以 BLOCK_SIZE_KV 大小的块流式处理：

forstart_kvinrange(lo, hi, BLOCK_SIZE_KV):

加载 BLOCK_SIZE_KV 个键值，计算部分注意力分数，更新在线 softmax 状态，丢弃该块，处理下一个。内存复杂度维持 O(N)。

每个程序实例只加载一个查询块，对应序列中一小部分 token。但这些 token 要正确计算注意力输出，必须关注序列里所有键值。这是自注意力定义决定的：每个查询都要和每个键比较。FlashAttention 没改这个算法要求，只改计算调度方式。键值逐块流式进来，累积到输出，立刻丢弃，内存占用小，结果精确。一些新的注意力变体（局部注意力、稀疏注意力、滑动窗口注意力）不会关注所有 token。

为 K 和 V 构建块指针

和 Q_block 一样，计算当前块的 token 索引：

kv_positions=start_kv+off_kv

然后构建指针：

K_block_ptr = (
k_ptr + qkv_offset_K
+ off_head[:, None] * kd_stride
+ kv_positions[None, :] * kn_stride
)

V_block_ptr = (
v_ptr + qkv_offset_V
+ kv_positions[:, None] * vn_stride
+ off_head[None, :] * vd_stride
)

得到形状 [HEAD_DIM, BLOCK_SIZE_KV] 的 K 和 V 指针。边界 mask 逻辑防止最后一个块越界访问：

mask_k = kv_positions[None, :] < SEQ_LEN
mask_v = kv_positions[:, None] < SEQ_LEN

从 HBM 加载 K 和 V 到片上 SRAM：

K_block = tl.load(K_block_ptr, mask=mask_k, other=0.0)
V_block = tl.load(V_block_ptr, mask=mask_v, other=0.0)

部分分数计算和在线更新

计算分块点积：

QK_block=tl.dot(Q_block, K_block)

应用缩放和 mask（如果是因果的），更新运行最大值：

mask = off_q[:, None] >= (start_kv + off_kv[None, :])
QK_block = QK_block * scale + tl.where(mask, 0, -1e6)
m_ij = tl.maximum(m_i, tl.max(QK_block, 1))
QK_block -= m_ij[:, None]
m_ij = tl.maximum(m_i, tl.max(QK_block, 1) * scale)
QK_block = QK_block * scale – m_ij[:, None]

更新在线 softmax 状态：

P_block = exp(QK_block)
l_ij = sum(P_block, axis=1)
alpha = exp(m_i – m_ij)
l_i = l_i * alpha + l_ij

更新输出累加器：

O_block = O_block * alpha[:, None]
O_block = dot(P_block, V_block, O_block)

用当前迭代找到的新最大值更新运行最大值：

m_i=m_ij

更新后的状态返回给外层内核 fwd_flash_attn_kernel。

最终归一化和写回

所有 K/V 块处理完后，前向内核完成输出：

O_block=O_block/l_i[:, None]

用累积的分母因子归一化注意力输出。当前查询块的注意力输出就算完了。

性能和基准测试

前向传播实现完毕并验证后，可以看看性能和标准注意力实现比较一下。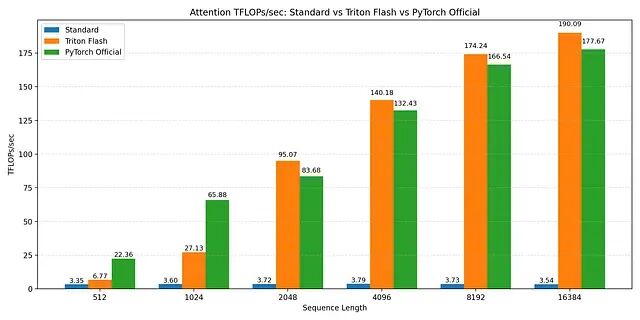

FlashAttention vs. standard attention vs torch2.2 (spda flashattn) TFLOP/s benchmarks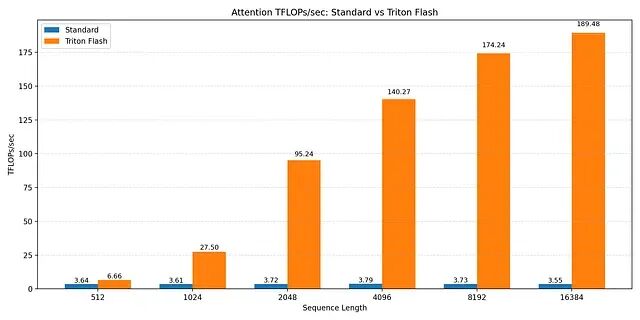

所有序列长度上标准注意力在 3-4 TFLOPs/sec 左右就到顶了。理论计算量虽然按 O(N²) 增长，但标准注意力被 HBM 流量主导。GPU 大部分时间在搬运 N × N 注意力矩阵，不是在做有用计算。序列变长并不能提高计算单元利用率，只是内存压力变大。

Triton FlashAttention 内核则随序列长度增加激进扩展。512 token 时性能一般，超过 2K token 后吞吐量快速上升。16K token 时维持在约 190 TFLOPs/sec。这正是 FlashAttention 设计要达到的效果：阻止注意力矩阵物化，中间数据驻留 SRAM，内存加载得以摊销。序列越长，内核越趋向计算受限，GPU 接近有效峰值吞吐量——和标准注意力恰好相反，标准注意力序列越长越内存受限。

第二张图在 Nvidia A100 上通过 sdpa API 比较了 Triton FlashAttention 和 PyTorch 官方 FlashAttention 实现。序列较短时 PyTorch 实现有竞争力，序列长度 ≥4k 后，自定义 Triton 内核追平并略微超过 PyTorch 性能。16k token 时，两者都收敛到约 180-190 TFLOPs/sec。

所有结果在同一 GPU（Nvidia A100 SXM）相同条件下获得。吞吐量以 TFLOPs/sec 报告，由缩放点积注意力的理论 FLOP 数除以实测内核运行时间得出。序列长度变化，batch 大小、头数、头维度固定。

这些基准验证了三件事：标准注意力从根本上内存受限；FlashAttention 把瓶颈从内存转到计算；Triton 提供了足够的数据移动和 GPU 内存底层控制，能达到接近最优性能。

关键是性能增益随序列长度增长。这正是 FlashAttention 在实践中最重要的地方。

总结

现代 GPU 上性能由内存行为主导，不是 FLOPs；内核融合和 SRAM 驻留比数学技巧更重要；在线 softmax 是 IO 感知注意力的关键；Triton 暴露了足够的硬件细节来写可读又快的内核；仔细分块加自动调优，自定义内核能和厂商实现打平。

FlashAttention 不是因为改了算法才更快，是因为它尊重 GPU 实际的工作方式。

本文只实现了前向传播。扩展到完整的训练级 FlashAttention（反向传播、dropout、各种 mask 变体）留待后续工作。

本文源代码：

https://avoid.overfit.cn/post/0ae6fbc34b7f4c1788f6399a7a1fc431

by Katherine Oluwadarasimi Olowookere