目录
Microsoft Word – 123518_fixed.docx
摘要
参考文献及链接
1. 引言
2. 双梳光谱仪的灵敏度
2.1 双梳光谱仪的配置
2.2 加性噪声的影响:探测器噪声、散粒噪声、激光相对强度噪声(RIN)和探测器动态范围
2.2.1 滤波和探测器数量的缩放规律
2.2.2 定量值与现有验证结果的对比
2.3 对痕量气体的灵敏度
2.4 光梳之间残余相位噪声导致的乘性噪声
2.5 与可调谐激光光谱仪和光栅光谱仪的对比
2.6 总结
3. 推导过程
3.1 系统响应
3.2 加性白噪声源的贡献
3.3 对已知气体的灵敏度
3.4 光梳间残余相位噪声导致的乘性噪声
致谢
内森・R・纽伯里 *、伊恩・科丁顿、威廉・斯旺美国国家标准与技术研究院,美国科罗拉多州博尔德市百老汇大街 325 号,邮编 80305*电子邮箱:nnewbury@boulder.nist.gov
摘要
相干双梳光谱法能够对样品响应的幅度和相位进行高分辨率、高精度的测量。本文探讨了由加性白噪声和乘性噪声导致的可实现信噪比(SNR),以及痕量气体检测的相应灵敏度极限。研究表明,在某些情况下,通过可调谐滤波器对整个光谱进行顺序采集,或通过探测器阵列进行并行采集,可显著提高信噪比。本文提出一个实用的品质因数作为性能指标,其等于信噪比(经采集时间平方根归一化后)与分辨频率元素数量的乘积。对于基于单探测器和光纤激光器的系统,该品质因数为10^6 – 10^7 Hz^(1/2)。
本研究为美国政府工作成果,不受版权限制。
OCIS 代码:(300.6320)外差光谱法;(300.6300)傅里叶变换光谱法
参考文献及链接
1. 引言
已有多项研究证明相干双梳光谱法 [1-8] 能够提供宽带光谱数据,且通常具有极高的频率精度和分辨率。在本文所考虑的配置中(参考文献 [6-8] 已充分验证),一束光梳的输出穿过样品后,与另一束 “本地振荡器”(LO)光梳源相结合,可利用光梳源固有的频率分辨率和精度,测量样品的完整复响应(即相位和幅度)。在时域中,该方法类似于时域光谱法 [7] 或色散傅里叶变换光谱法(FTS)[9-12];在频域中,其类似于大规模并行激光外差光谱仪,每对光梳齿都会在特定射频频率下产生外差信号 [13]。尽管该技术能够以高频率精度和分辨率提供复响应(相位和幅度),但可实现的信噪比(SNR)受限于常规因素,即探测器噪声、散粒噪声、激光技术噪声和探测动态范围。低信噪比无疑会削弱该方法的诸多优势,例如,寻找宽光谱线的线心时,其统计极限由信噪比决定,可能会超出光梳固有的精度。本文推导了缩放定律和定量信噪比表达式,并研究了该技术的灵敏度。这些表达式可用于系统设计、系统性能评估以及与更传统方法的对比。
本文推导了三个主要方程。首先,给出了由探测器噪声、散粒噪声、额外激光相对强度噪声(RIN)和探测器动态范围导致的极限信噪比,并指出了对整个光谱进行顺序或并行采集的潜在优势,同时与可调谐激光光谱仪进行了对比。其次,给出了痕量气体检测的相应灵敏度极限。第三,分析了由乘性噪声(尤其是光梳之间的残余载波相位噪声)导致的信噪比限制。研究表明,在适当的工作参数下,通过有源锁相 [6-8] 或有源监测 [4] 来抵消光梳之间的相对相位和定时抖动,该乘性噪声可忽略不计。推导过程简洁明了,最终的缩放定律与传统傅里叶变换光谱法 [14-16] 和激光光谱法 [17,18] 中的相关表达式密切相关。因此,本文在第 2 节中呈现并讨论基本结果,第 3 节再给出详细推导过程。
2. 双梳光谱仪的灵敏度
2.1 双梳光谱仪的配置
相干双梳光谱法可视为穿过样品的源光梳与重复频率不同的本地振荡器(LO)光梳之间的大规模并行多外差测量。源光梳和本地振荡器光梳的每对光梳齿都会形成各自的射频拍频信号,从而将光学响应下变频至射频域。在时域中,该方法本质上是傅里叶光谱法,涉及采集源光梳脉冲Es(t)和本地振荡器光梳脉冲\\(E_{LO}(t)\\)之间的干涉图(或互相关);连续脉冲对之间的重叠具有等于脉冲周期差的有效时间步长,因此本地振荡器脉冲会缓慢扫过信号脉冲。在这种情况下,无样品时的数字化电压为Vref(t)=S(t)⊗Es(t)(作为有效时间t的函数),其中⊗表示卷积,
![]() 为采样函数(参考文献 [19] 中的方程(12)给出了更精确的S(t)表达式,可保留多外差频域图像)。当存在时域响应为H(t)的样品时,数字化电压为V(t)=S(t)⊗Es(t)⊗H(t)。目标是分离出样品响应,这在频域中可通过以下比值轻松实现:
为采样函数(参考文献 [19] 中的方程(12)给出了更精确的S(t)表达式,可保留多外差频域图像)。当存在时域响应为H(t)的样品时,数字化电压为V(t)=S(t)⊗Es(t)⊗H(t)。目标是分离出样品响应,这在频域中可通过以下比值轻松实现:
\\begin{equation} \\tilde{H}(\\nu) = \\frac{\\tilde{V}(\\nu)}{\\tilde{V}_{ref}(\\nu)} = \\tilde{H}_0(\\nu) + \\sigma_H \\tag{1} \\end{equation}
其中,波浪号表示傅里叶变换,v为光频,$\\tilde{H}_0\\left(\\nu\\right)$为真实样品响应,σH为不可避免的附加噪声(本文后续将围绕该噪声展开讨论)。对于弱吸收样品,$\\tilde{H}_0(\\nu) \\equiv 1 + 4\\pi^2 i c^{-1} \\nu \\chi(\\nu) L \\approx 1 – \\alpha(\\nu) L/2 + i \\Delta k(\\nu) L$,其中$\\chi$为线性极化率,L为样品长度,α(v)为衰减系数,Δk(v)为相移。
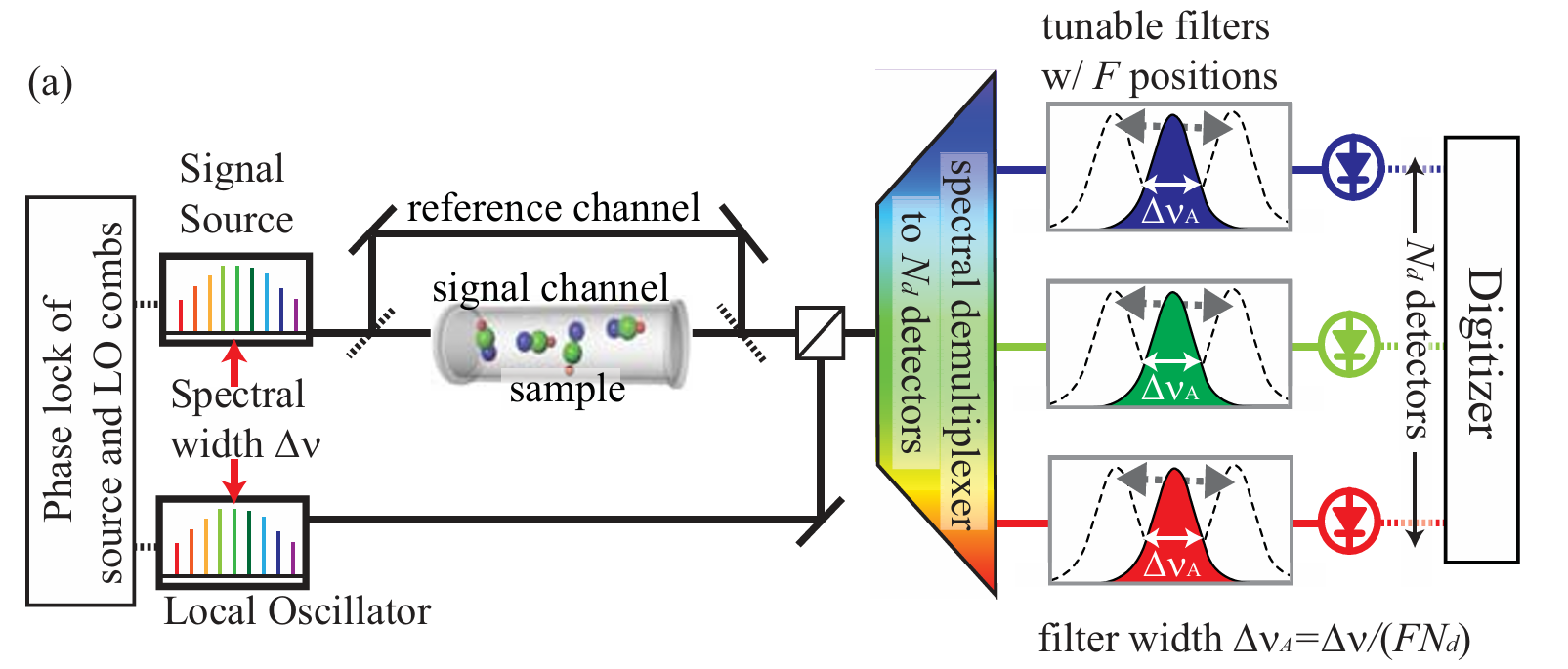
图 1. (a)双梳光谱仪布局示意图,包括顺序或并行数据采集的可能性。图中,信号和参考采用时分复用 [7,8],但参考也可在单独的干涉仪 [6] 中采集,或通过空样品池顺序采集。
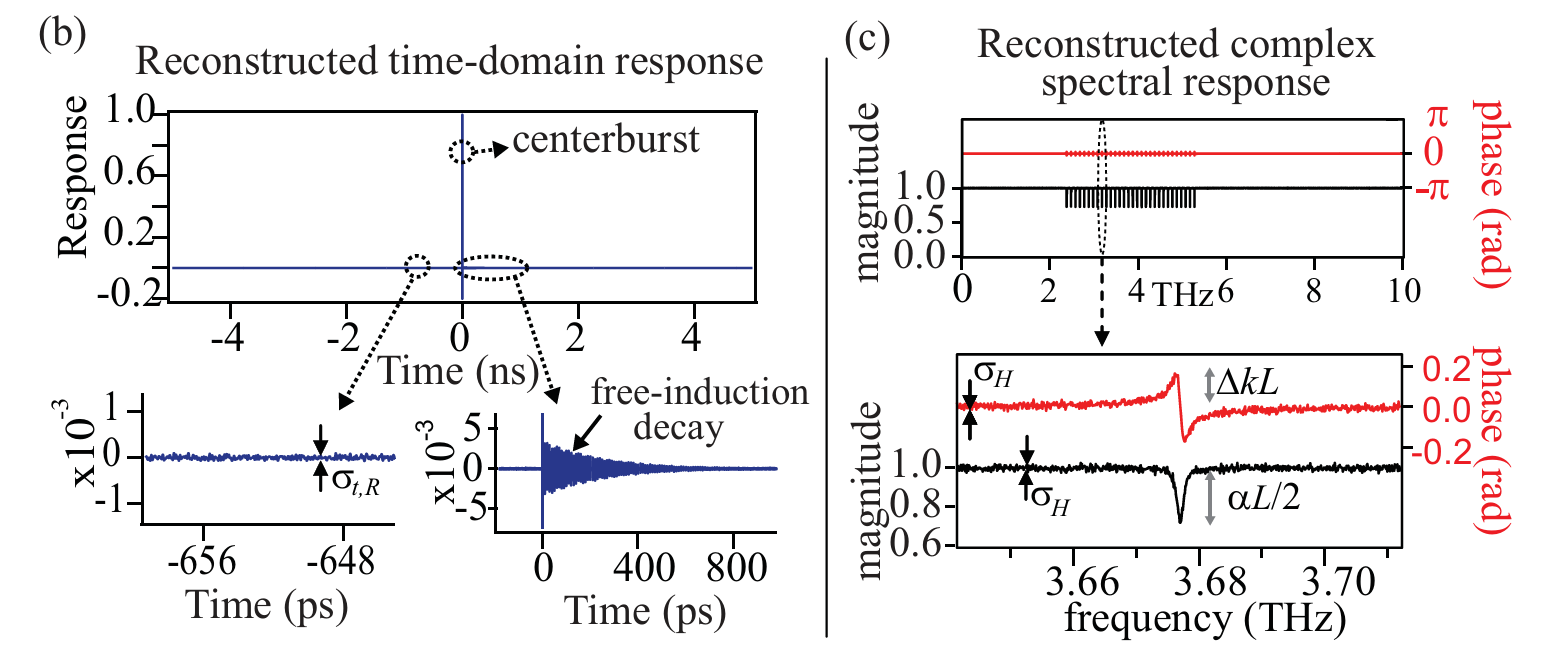 图 1. (b)模拟时域信号与有效下变频时间(非实验室时间)的关系。(c)在 10 太赫兹带宽、100 兆赫兹分辨率下(M=100,000个分辨元素)对应的频域样品响应。为便于说明,假设样品具有 20 条等间距、宽度为 2 吉赫兹的洛伦兹跃迁线,频域信噪比为$\\sigma_H^{−1}=100$。在时域中,相应信号为单边干涉图,包含两个分量:中心脉冲和尾随的自由感应衰减信号。在频域中,每条跃迁线的幅度和相位都得到了高分辨率的分辨。
图 1. (b)模拟时域信号与有效下变频时间(非实验室时间)的关系。(c)在 10 太赫兹带宽、100 兆赫兹分辨率下(M=100,000个分辨元素)对应的频域样品响应。为便于说明,假设样品具有 20 条等间距、宽度为 2 吉赫兹的洛伦兹跃迁线,频域信噪比为$\\sigma_H^{−1}=100$。在时域中,相应信号为单边干涉图,包含两个分量:中心脉冲和尾随的自由感应衰减信号。在频域中,每条跃迁线的幅度和相位都得到了高分辨率的分辨。
本文考虑图 1 所示的通用配置,其设计基于以下考量:尽管傅里叶光谱法可显著降低探测器噪声的影响(费尔盖特优势),但会放大额外源噪声和动态范围限制的影响 [9,10,14,16]。通过将测量光谱(Δv)分解为可顺序或并行采集的子带,可减轻这些噪声项的影响。并行采集通过固定滤波器实现,该滤波器将$N_d$个光谱滤波后的子带多路复用到$N_d$个探测器阵列;顺序采集通过每个探测器前的可调谐光学带通滤波器实现,该滤波器可扫描F个不同的滤波带。总体而言,总光谱带宽被划分为F×$N_d$个子带,每个子带的滤波带宽为$\\Delta \\nu_A = \\Delta \\nu / \\left( F N_d \\right)$。每个子带的测量时间为T/F(T为总采集时间)。在每个子带内,根据方程(1)计算响应。光梳的稳定性使得能够将这些子带的全带宽特征相干拼接,同时保留频率分辨率和精度。除了可能提高信噪比外,这种光谱分解还允许光梳重复频率差Δfr更大(同时仍满足奈奎斯特约束)。由于该频率差Δfr恰好是下变频射频外差拍频信号之间的间隔,因此Δfr越大,对光梳相对线宽的要求就越低。滤波还有助于归一化光梳光谱中的强光谱变化 [8]。然而,需权衡的是,光谱分解也会放大乘性噪声(见第 2.4 节),且可能增加时间开销。
本文的分析基于以下假设:
2.2 加性噪声的影响:探测器噪声、散粒噪声、激光相对强度噪声(RIN)和探测器动态范围
在噪声方面,本文考虑探测器噪声、散粒噪声和额外相对强度噪声(RIN)。探测器噪声由等效噪声功率(NEP)表征,包括直至信号数字化的所有加性噪声项(如暗电流、约翰逊噪声、放大器噪声系数等)。等效噪声功率(NEP)会因波长波段和探测器类型的不同而显著变化。本文假设外差信号的频率足够高,远离任何 “1/f” 探测噪声,因此等效噪声功率(NEP)为白噪声。散粒噪声可通过光电探测器处的光梳功率轻松计算。激光相对强度噪声(RIN)可能包含来自脉冲间变化的低频分量,以及来自激光器或后续任何光放大过程中发射的附加放大自发辐射(ASE)的全频率分量。低频分量可能导致乘性噪声,但本文假设干涉图更新率(等于Δfr)快于该低频噪声,因此忽略该分量。或者,可通过有源反馈实验抑制该相对强度噪声(RIN)分量,或通过单独测量抵消。因此,本文仅考虑由附加放大自发辐射(ASE)导致的白噪声、宽带相对强度噪声(RIN),并假设放大自发辐射(ASE)与光梳输出具有相同的均匀光谱形状。最后,本文还考虑了由数字化仪、放大器或最终由光电探测器本身设定的探测动态范围限制。
通过仅考虑上述白噪声、宽带噪声源,本文本质上假设源光梳和本地振荡器(LO)光梳是 “理想” 的(除附加放大自发辐射(ASE)的影响外)。然而,光梳之间仍会存在残余定时和载波相位噪声,可能导致乘性噪声。在第 2.4 节和第 3.4 节中,本文将考虑由载波相位抖动导致的乘性噪声(其可能主导定时抖动的影响)。研究表明,只要光学滤波器带宽足够大,且通过有源反馈或监测充分抑制相位抖动,乘性噪声可忽略不计。
方程(1)中$\\tilde{H}\\left(\\nu\\right)$的测量结果给出了覆盖带宽Δv、包含M个分辨光谱元素的一组复数值点。仅考虑宽带噪声贡献时,光谱中每个光谱元素的幅度或相位(以弧度为单位)的平均不确定度为:\\begin{equation} \\sigma_H = \\frac{M\\sqrt{\\varepsilon}}{0.8\\sqrt{T}} \\left\\{ a_{NEP} \\frac{F}{P_c^2} + a_{shot} \\frac{1}{N_d P_c} + \\left( a_{RIN} + a_{range} \\right) \\frac{1}{N_{\\text{d}}^2 F} \\right\\}^{1/2}, \\tag{2} \\end{equation}
其中变量定义如表 1 所示(方程(2)的推导过程见第 3.2 节)。信噪比(SNR)即为1/σ$_H$。求和项中的前两项分别为探测器噪声和散粒噪声,最后一项反映了由激光相对强度噪声(RIN)或探测动态范围设定的脉冲测量限制。ε考虑了所需分辨率与光梳重复频率设定的分辨率之间的不匹配,可视为时域中的占空比修正。在傅里叶变换光谱法(FTS)中,理论上不存在该修正项(因为扫描长度将与所需分辨率匹配,尽管如此,由于反射镜的反转时间,传统傅里叶变换光谱法(FTS)仍会有类似项)。值得注意的是,重复频率差的调制 [2] 原则上可降低该占空比因子。
表 1. 变量定义
| 源光梳功率(瓦) | Pc | 光谱宽度(赫兹) | Δv |
| 源光梳与本地振荡器(LO)光梳功率比 | γ | 光梳重复频率(赫兹) | fr |
| 本地振荡器(LO)光梳功率(瓦) | γPc | 光谱分辨率(赫兹) | νres |
| 探测器噪声(瓦 / 赫兹1/2) | NEP | 分辨元素数量 | M=Δv/νres |
| 探测动态范围 | D | 占空比 | ε≡νres/fr |
| 激光相对强度噪声(RIN) | RIN | 滤波器位置数量(顺序采集程度) | F |
| 探测器效率 | η | 探测器数量(并行采集程度) | Nd |
| 平衡探测因子 | b | – | – |
系数:
\\begin{align*} a_{NEP} &= \\gamma^{-1} NEP^2 \\\\ a_{shot} &= 4 c_\\gamma \\eta^{-1} h\\nu \\\\ a_{RIN} &= 2 c_{\\gamma^2} b RIN \\\\ a_{range} &= 8 D^{-2} f_r^{-1} \\end{align*}
注:a 相关常数为cγ=(1+γ)/(2γ)和cγ2=(1+γ^2)/(2γ),γ与传统傅里叶变换光谱法(FTS)中的调制效率密切相关。b 具体而言,源光梳或本地振荡器(LO)光梳的重复频率为frS或frL。c 动态范围可与有效位数N相关联,即$D = \\sqrt{3}\\ 2^N$[16]。对于N=12,D≈7000。d 相对强度噪声(RIN)为单边噪声,通常以分贝每赫兹(dBc/Hz)表示。e 探测可采用平衡探测(b=1)或非平衡探测(b=2)。
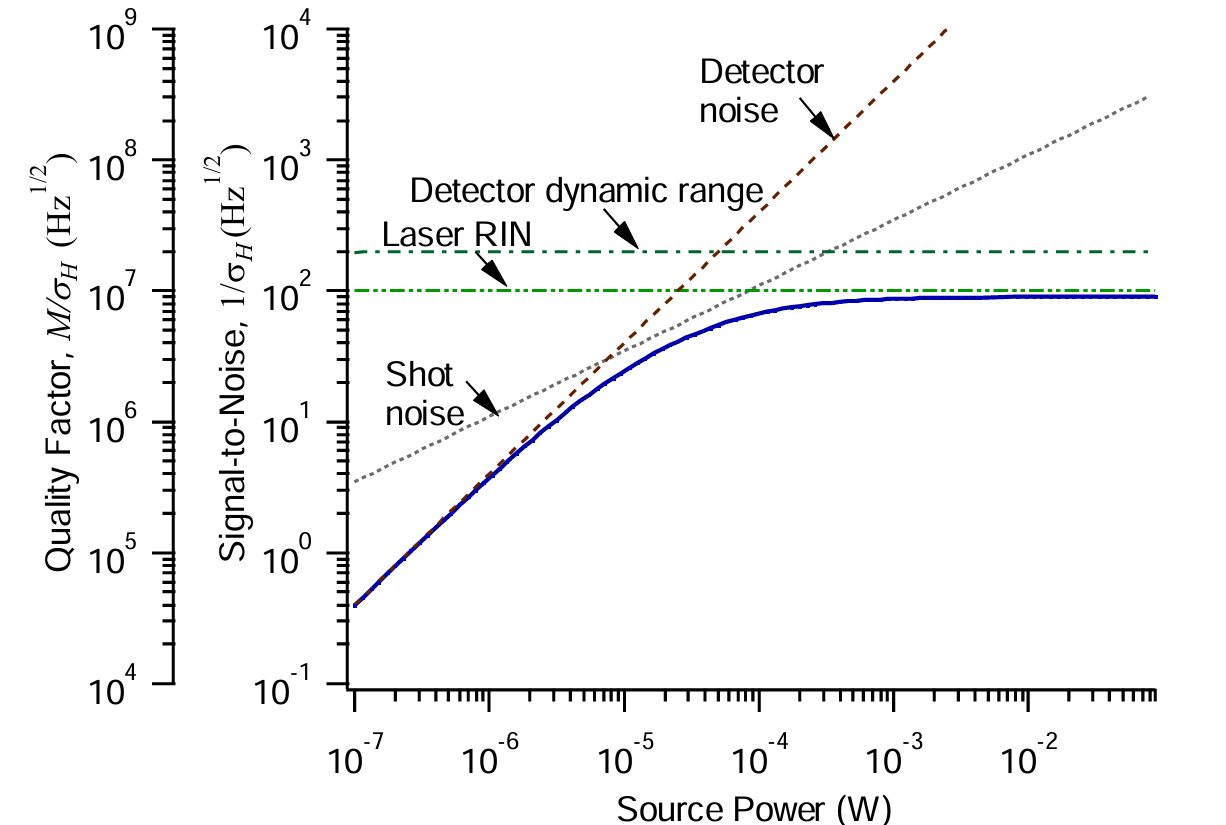
图 2. 单探测器、无光学滤波(F=Nd=1)时,双梳光谱仪的信噪比和品质因数与总光梳功率Pc的关系(基于方程(2),归一化到 1 秒总采集时间)。品质因数是分辨光谱元素数量与幅度或相位信噪比的乘积。图中还展示了M=100,000个分辨元素时的信噪比。在低光梳功率下,信噪比(或品质因数)(蓝色实线)受探测器噪声限制(棕色长虚线);在中等光梳功率下,受散粒噪声限制(灰色短虚线);在高光梳功率下,受激光相对强度噪声(RIN)(浅绿色点划线)或探测器动态范围限制(深绿色点划线)。假设光谱均匀且滤波器形状为高斯型,每个光梳齿的平均功率为Ptout=0.8Pcfr/Δv。使用的参数值:NEP=2皮瓦 / 赫兹1/2,D=7000,RIN=−145分贝每赫兹(dBc/Hz),η=0.9,b=1,ε=1,γ=cγ=cγ2=1,Δv=10太赫兹,fr=vres=100兆赫兹。
根据方程(2),无论主导噪声为何,不确定度均与M成线性比例。在傅里叶光谱法中,由于每个干涉图约有M个时间步长,因此预期存在$M^{1/2}$的依赖关系。在双梳光谱法中,额外的$M^{1/2}$依赖关系源于假设激光功率恒定,因此光谱宽度加倍会降低源光谱功率密度(而在传统傅里叶变换光谱法(FTS)中,由于源功率光谱密度固定,通常不存在该依赖关系)。从缩放规律和实际应用角度出发,一个实用的性能指标是归一化品质因数,即T=1秒时的M/σ$_H$[9],或单位时间信噪比与分辨光谱元素数量的乘积。图 2 绘制了品质因数和信噪比随总光梳功率的变化曲线。在以下小节中,本文将讨论方程(2)的其他结果。
2.2.1 滤波和探测器数量的缩放规律
图 3 展示了品质因数和信噪比随顺序或并行光谱采集程度(由F和Nd量化)的缩放规律,所有量均归一化到相同的 1 秒总采集时间。在探测器噪声限制下(低Pc),如费尔盖特优势所预期的,顺序采集(F>1)存在明显劣势,且多探测器无优势;在散粒噪声限制下(中等Pc),无论光谱是顺序测量还是一次性测量,均可达到相同的信噪比,但多探测器具有优势;最后,在相对强度噪声(RIN)或动态范围限制下(高Pc),顺序采集具有优势,多探测器的优势更为显著。
增加整体滤波程度NdF会降低特定探测器上的光功率,并将限制噪声从相对强度噪声(RIN)或动态范围转变为散粒噪声或探测器噪声。理想情况下,应增加探测器数量Nd,直到噪声受探测器噪声限制。但在实际应用中,多探测器的使用必须与系统复杂度的相应增加相权衡,因此Nd可能限制为 1。此时,仍可通过增加顺序滤波F,直到相对强度噪声(RIN)或动态范围不再起主导作用。基于方程(2),最优光谱滤波值为$F_{opt} \\approx P_c \\sqrt{2 RIN} / \\left( N_d NEP \\right) $(针对大D和ε=b=γ=$c_{\\gamma^2}$=1)。对于图 1 中的参数值和Pc=2毫瓦,可得Fopt≈100$N_d^{−1}$,对应于 1550 纳米处 10 太赫兹光源的约 1 纳米带宽滤波。考虑到需要抑制乘性噪声的影响(见第 2.5 节),该带宽可能过窄,因此系统可能在稍宽的滤波水平下运行。
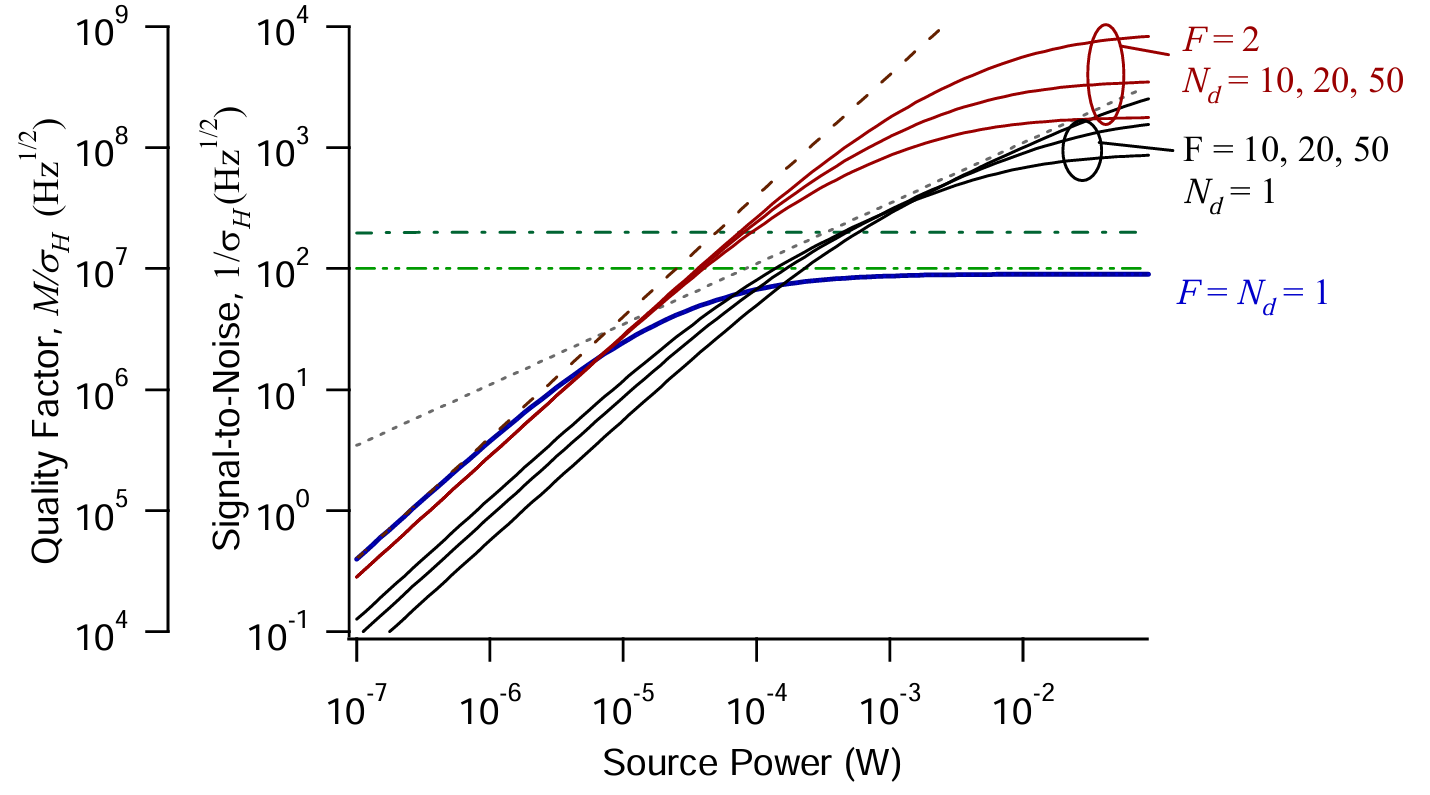
图 3. 在与图 2 相同的条件下,不同顺序采集(F=10、20、50,Nd=1,黑色线)和并行数据采集(Nd=10、20、50 个探测器,F=2,红色线)时,M=100,000个分辨元素的品质因数和信噪比与总光梳功率Pc的关系。为便于参考,图中还保留了图 2 中的其他线条。低功率下,顺序采集会带来损耗,但在高光梳功率下,可消除激光相对强度噪声(RIN)或探测器动态范围带来的限制。未包含乘性噪声的影响(见第 2.4 节)。(Nd>1的曲线使用F=2,因为可能采用交错方法。)
2.2.2 定量值与现有验证结果的对比
一般而言,对于在激光器或放大器增益带宽附近运行的系统,光梳功率可能足够高,因此方程(2)中的限制噪声项预期为相对强度噪声(RIN)/ 动态范围项(至少对于低F和Nd)。对于超连续谱源,由于相对强度噪声(RIN)的恶化 [21-23],该噪声项也可能起主导作用。在这种限制下,当b=γ=cγ2=1时,方程(2)可重写为品质因数的简化表达式:
\\begin{equation} \\frac{M}{\\sigma_H} = 0.8 \\frac{N_d \\sqrt{T}}{\\sqrt{\\varepsilon}} \\sqrt{\\frac{F}{2 RIN + 8 D^{-2} f_r^{-1}}} \\tag{3} \\end{equation}
本文测量的光纤激光器相对强度噪声(RIN)最低可达10−15(即 – 150 分贝每赫兹(dBc/Hz)),但经过放大后,更实际的数值为 – 145 分贝每赫兹(dBc/Hz),且显著的光谱展宽可能导致相对强度噪声(RIN)进一步升高。动态范围贡献项$8 D^{-2} f_r^{-1}$在 12 位时为 – 148 分贝每赫兹(dBc/Hz),在 8 位时为 – 124 分贝每赫兹(dBc/Hz)[16]。因此,根据系统情况,激光相对强度噪声(RIN)或动态范围均可能主导方程(3)。作为实用基准,当M=100,000个分辨元素、单探测器无滤波且RIN=−145分贝每赫兹(dBc/Hz)时,信噪比1/σH≈100T1/2。
在本文近期的研究 [7,8] 中,光谱中心的信噪比受限于较差的动态范围(D≈500),光谱边缘的信噪比受探测器噪声限制。对于相应的$8 D^{-2} f_r^{-1}$=−125分贝每赫兹(dBc/Hz)以及实验参数F≈45和ε=2,方程(3)得出M/σH=6.7×106赫兹1/2。在测量的M=41000、σH=4×10−4和T=2700秒时,测量的品质因数为M/σH=2×106赫兹1/2,比计算值低约 3 倍,这主要归因于光谱边缘光梳功率降低导致的信噪比下降(峰值信噪比约高 2 倍)以及源光梳和本地振荡器(LO)光梳功率不相等。
本文还可将方程(3)与其他几项基于光纤的双梳光谱法验证结果 [4,5] 进行对比。在参考文献 [5] 的初始腔增强验证中,存在M=1500个分辨元素。包括参考扫描在内,峰值信噪比=100/2,采集时间T=2Δfr−1≈4毫秒(参考文献 [5] 中引用的采集周期为切趾窗口,但在方程(2)中为完整扫描所需的时间或Δfr−1)。根据这些数值,实验品质因数为M/σH=1.7×10^6赫兹1/2。在参考文献 [4] 中,两束源光均穿过样品,但信噪比应仍在 2 倍范围内适用。本文估计M≈3100、ε=115、幅度信噪比为2×100、采集时间T=2秒,计算得出M/σH≈0.25×10^6赫兹1/2(当Δfr接近奈奎斯特极限时,可能获得更高值)。
总体而言,对于单探测器,这些结果以及方程(3)和图 2 表明,相干双梳光谱法的品质因数M/σH<107赫兹1/2(至少对于基于光纤的光梳);固态光梳的相对强度噪声(RIN)更低,可能达到更高的品质因数。
2.3 对痕量气体的灵敏度
重建的响应为样品表征提供了高频率分辨率和精度,因此有望在存在大量背景干扰的情况下检测特定气体。基于方程(2),可计算最佳可能灵敏度(无背景干扰)。为与激光光谱仪对比,将灵敏度表示为离散谱线处的最小吸收灵敏度(α0L)min。简单而言,可将其等同于光谱强度的不确定度2σH。但实际灵敏度会显著更高,因为单条吸收线和多条吸收线均存在多个测量点:\\begin{equation} \\left( \\alpha_0 L \\right)_{\\text{min}}^{\\text{effective}} = 2 \\sigma_H \\times \\sqrt{\\frac{4 \\nu_{\\text{res}}}{\\pi \\sum_j \\Delta \\nu_{Lor,j} \\left( \\alpha_j / \\alpha_0 \\right)^2}}, \\tag{4} \\end{equation}
其中求和项覆盖不同的振转线,每条线具有洛伦兹半高宽(FWHM)ΔvLor,j和峰值吸收αj。平方根项表示相对于单个频率元素计算的灵敏度增强。对于图 1 中的模拟信号,求和项覆盖 20 条强度相等、宽度约为20×vres的谱线,增强因子约为 20。更实际地,例如对于参考文献 [6-8] 中的氰化氢(HCN)数据,当vres=200兆赫兹时,相对于最强线的增强因子约为 11。方程(4)还假设气体响应已知。尽管这种增强有助于提高灵敏度,但与激光光谱仪的标准相比,整体灵敏度仍然较低。与传统傅里叶变换光谱法(FTS)一样,这种较低的灵敏度是与宽带光谱获取能力的权衡。
2.4 光梳之间残余相位噪声导致的乘性噪声
任何傅里叶光谱法中都存在一个重要的噪声贡献 —— 乘性噪声,其可能源于两台光梳源之间的相对幅度噪声、定时抖动或相位噪声(散粒噪声在技术上是乘性的,但出于第 3.2 节中解释的原因,本文将其视为加性噪声)。本文假设通过有源锁相或监测方法 [4,6-8],大部分光梳之间的定时和相位噪声已被抑制(原则上,也可通过类似方式抑制脉冲间幅度噪声)。然而,光梳之间仍会存在残余噪声,因此计算该噪声对测量样品响应的影响具有重要意义。即使对于高度稳定的光梳 [20],载波相位噪声也尤其棘手,因此本文重点关注载波相位噪声而非定时抖动。可将相位噪声分为慢速和快速分量:慢于干涉图更新率Δ$f_r^{−1}$的相位噪声会导致求和干涉图信号降低$\\left(1 – \\sigma_{\\varphi,slow}^2 / 2\\right)$,其中$\\sigma_{\\varphi,slow}^2 $是相位变化的(慢速)分量。当$\\sigma_{\\varphi,slow}^2 $=0.4弧度时,净影响仅为可忽略的 8% 降低 [19];当$\\sigma_{\\varphi,slow}^2 $>1弧度时,应采用常规方法 [8,16] 进行相位校正。因此,慢速相位噪声通常不会构成问题。
在干涉图时间尺度上(尤其是中心脉冲期间)发生的残余快速相位噪声无法通过类似方式消除。假设噪声较小(<1 弧度),其会添加一个乘性噪声项,该噪声项会随着干涉图数量的平方根平均减小,但仍可能轻易超过加性白噪声。例如,0.1 弧度的变化会导致中心脉冲约 10% 的噪声,这将完全掩盖任何微弱的潜在信号。为了在时域中保留对样品响应(即痕量气体的自由感应衰减(FID)信号)的灵敏度,中心脉冲持续时间(~1/ΔvA)必须短于样品相干时间(~ 光谱特征宽度的倒数)。在频域中,这种乘性噪声导致相位和幅度噪声的相关宽度等于特定子带中信号的光谱宽度(例如ΔvA),从而产生慢速基线漂移。为了在频域中保留对样品响应的灵敏度,相关宽度ΔvA必须大于光谱特征的宽度(与时域中的条件完全相同)。可通过简单的多项式拟合消除慢速漂移 [6-8]。假设脉冲间方差为$\\sigma_{\\varphi,fast}^2$的白载波相位噪声,且滤波器中心之间的间隔等于半高宽(FWHM),则幅度或相位的噪声大致为:
\\begin{equation} \\sigma_{H,mult} \\sim 3\\sqrt{\\frac{\\Delta v}{T N_d f_r}} \\sigma_{\\varphi,fast}, \\tag{5} \\end{equation}
其中相关宽度为高斯型,等于滤波器的光谱宽度或ΔvA,变量定义如表 1 所示(更严格的表达式见方程(30))。可将该噪声与方程(2)中的白噪声进行对比。对于Nd=1和图 1 中的参数值,$\\sigma_{H,mult} \\sim 0.1\\sigma_{\\varphi,fast}\\ \\text{Hz}^{-1/2}$(注意,相对相位噪声的散粒噪声贡献为$\\sigma_{\\varphi,fast}^{shotnoise} \\sim n_c^{-1/2}$,其中nc为每个脉冲的光子数。将其代入方程(5),得到的噪声贡献比方程(2)中的等效散粒噪声贡献小约根号M倍)。总体而言,尽管该乘性噪声可能大于加性白噪声,但它在整个光谱中具有高度相关性;其对宽度为ΔvL的光谱线的噪声贡献仅为![]() 。例如,在参考文献 [7,8] 中,
。例如,在参考文献 [7,8] 中,![]() ,但由于ΔvA>100ΔvL,乘性噪声可忽略不计。因此,通过结合抑制光梳之间的残余噪声和傅里叶光谱法固有的共模抑制,双梳光谱法中的乘性噪声可被抑制到无关紧要的水平。当然,随着顺序或并行滤波程度的增加,ΔvA会减小,有效共模抑制也会相应降低,因此必须始终确保该噪声贡献低于方程(2)中的噪声水平。
,但由于ΔvA>100ΔvL,乘性噪声可忽略不计。因此,通过结合抑制光梳之间的残余噪声和傅里叶光谱法固有的共模抑制,双梳光谱法中的乘性噪声可被抑制到无关紧要的水平。当然,随着顺序或并行滤波程度的增加,ΔvA会减小,有效共模抑制也会相应降低,因此必须始终确保该噪声贡献低于方程(2)中的噪声水平。
2.5 与可调谐激光光谱仪和光栅光谱仪的对比
将双梳光谱仪的信噪比与覆盖相同带宽、具有相同分辨率的可调谐激光光谱仪(TLS)[17,18] 进行对比也具有重要意义。首先,将双梳光谱仪(单探测器、无滤波,F=Nd=1)与可调谐激光光谱仪(TLS)对比,忽略与几何相关的数值因子,并假设相对强度噪声(RIN)和光梳光谱在光谱上是平坦的。在探测器噪声限制下,双梳光谱仪等效于功率为$\\sqrt{N_{teeth}}\\,P_{tooth}$的可调谐激光光谱仪(TLS),其中Ptooth为每个齿的功率,Nteeth=Δv/fr为参与的光梳齿数量(当ε=1时等于M)。当然,可调谐激光光谱仪(TLS)不太可能受探测器噪声限制。在散粒噪声限制下,双梳光谱仪等效于功率为Ptooth的可调谐激光光谱仪(TLS)。在相对强度噪声(RIN)限制下,双梳光谱仪等效于相对强度噪声(RIN)大Nteeth倍的可调谐激光光谱仪(TLS)。如果采用顺序或并行采集,对比结果会有所改善。例如,在散粒噪声限制下,双梳光谱仪等效于功率为NdPtooth的可调谐激光光谱仪(TLS);在相对强度噪声(RIN)限制下,等效于相对强度噪声(RIN)为$N_{teeth} RIN \\big/ \\left(N_d^2 F\\right)$的可调谐激光光谱仪(TLS)。
与可调谐激光光谱仪(TLS)相比,双梳傅里叶变换光谱法(FTS)还具有以下几个额外优势:
2.6 总结
本文推导了双梳光谱仪可实现的基本信噪比(方程(2)),考虑了在微分啁啾可忽略、奈奎斯特滤波以及光梳之间 “1/f” 噪声可忽略的假设下,来自探测、散粒噪声或由附加放大自发辐射(ASE)导致的相对强度噪声(RIN)的加性白噪声的影响。后一假设要求通过有源反馈或误差信号监测,将扫描速率(Δfr)设置得足够高,并实现光梳之间的有效锁相。本文表明,在适当条件下,乘性噪声可控制在方程(2)的噪声水平以下。同时,考虑方程(2)中的加性噪声,推导了痕量气体检测的有效信噪比。本文还考虑了通过可调谐滤波器顺序采集、通过固定滤波器和探测器阵列并行采集或一次性采集整个光谱的可能性。
这些方程可根据不同噪声源的贡献,指导双梳光谱仪的设计。例如,在适当处理乘性噪声的情况下,使用探测器阵列的双梳光谱仪可获得最佳信噪比。从信噪比的缩放规律和实际应用角度出发,一个实用的性能指标是品质因数(由分辨元素数量与信噪比的乘积给出)。对于基于光纤的系统,该品质因数约为10^6赫兹1/2-10^7赫兹1/2;然而,这些方程具有通用性,也适用于未来中红外和长波红外区域的双梳光谱法。测量特定气体光谱的灵敏度极限由信噪比、总光程长度(通过腔增强或多通池,这些系统的总光程长度可相当大)以及可实现的总积分周期(通过相干信号平均,总积分周期也可相当大)决定。尽管双梳光谱仪的灵敏度不如可调谐激光光谱仪,但由于其出色的频率分辨率和精度、高采集速度以及能够访问可调谐激光器无法覆盖的光谱区域,因此在多种气体的宽带检测和高分辨率光谱法中具有广阔的应用前景。
3. 推导过程
本节的结构与第 2 节一致,即第 3.1 节推导系统的基本响应,第 3.2 节考虑加性噪声,第 3.3 节分析痕量气体灵敏度,第 3.4 节讨论乘性噪声。为便于深入理解,推导过程将同时在数据采集的时域和常用的频域中进行。
如图 1 所示,单个探测器在采集周期TA=T/F内将观测到宽度为ΔvA=Δv/(FNd)的 “瞬时” 光谱子带。每个光谱子带内的响应在频域中拼接,以覆盖完整的源带宽Δv(然后进行逆傅里叶变换以获得时域响应)。假设光谱功率大致均匀,则子带ΔvA内的光谱信噪比与全带宽Δv内的光谱信噪比相同,因此只需计算子带内的信噪比。为表示滤波后的物理量,将在表 1 中的变量后添加下标 “A”。
3.1 系统响应
在双梳光谱法中,源光梳和本地振荡器(LO)光梳的脉冲重复周期不同,分别为TS和TL,因此本地振荡器(LO)光梳脉冲每经过一个本地振荡器(LO)光梳脉冲周期,就会相对于源光梳脉冲前进ΔT=TL−TS,从而产生时域下变频因子:
\\begin{equation} K \\equiv \\frac{T_s}{\\Delta T} = \\frac{T_L}{\\Delta T} – 1. \\tag{6} \\end{equation}
该因子将实验室时间与有效时间相关联(本文假设ΔT>0)。本地振荡器(LO)光梳脉冲单次扫过源光梳脉冲会生成一个包含K个点的干涉图,耗时Δfr−1。类似地,在频域中,重复频率frS=TS−1和frL=TL−1的差值为Δfr=frS−frL,因此它们的外差信号是重复频率为Δfr的射频光梳,产生频域下变频因子 [1-8,13]:
\\begin{equation} K \\equiv \\frac{f_{rL}}{\\Delta f_r} = \\frac{f_{rS}}{\\Delta f_r} – 1. \\tag{7} \\end{equation}
如先前研究 [19] 所指出的,为实现完全同步采样,希望每个时域干涉图都相同,以便直接相加。在频域中,射频频率光梳恰好落在测量频率网格上(这并非必需 [4],但可简化计算)。为实现这一点,本文假设 [19]:
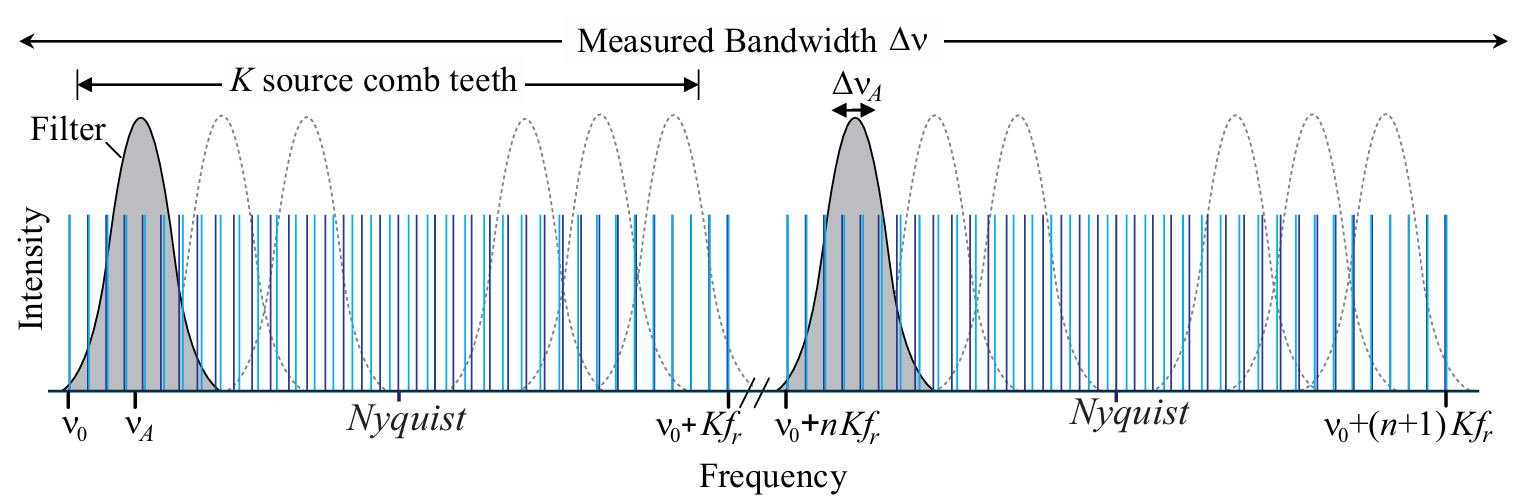
图 4. 计算中涉及的不同光频示意图。浅蓝色(深蓝色)线表示源光梳(本地振荡器(LO)光梳)齿,其重复频率差为Δfr。总测量带宽为Δv,但对于任何给定的干涉图,带宽通过滤波器滤波至ΔvA(可通过滤波器在光谱上顺序调谐,或通过固定滤波器组并行调谐至多个探测器,或两者结合)。注意射频拍频位于零频率或奈奎斯特频率处的 “死区”;在这些滤波器位置,需对一束源光进行整体频移 [7,8]。
在上述假设 1 和假设 2 下,源光梳和本地振荡器(LO)光梳的电场为:
\\begin{equation} E_S(t) = e^{i\\varphi_S} e^{-i2\\pi v_0 t} \\sum_n A_S\\left(t – nT_S\\right),\\ E_L(t) = e^{i\\varphi_S+\\Delta\\varphi} e^{-i2\\pi v_0 t} \\sum_m A_L\\left(t – mT_L\\right), \\tag{8} \\end{equation}
其中n和m为脉冲索引,φs和Δφ为相位因子,v0为公共共享光梳齿,AS(L)为电场包络。这些方程描述了频率为vn=v0±nfrS和vm=v0±mfrL(n、m为整数)的两束光梳。本文假设源光梳和本地振荡器(LO)光梳穿过相同的光谱滤波器,因此AL和AS具有相同的载波频率vA−v0和带宽ΔvA。如前所述,假设微分啁啾可忽略不计。
探测电压的外差部分为:\\begin{equation} V'(t) = aR(t) \\otimes E_L^{*}(t) E_S(t), \\tag{9} \\end{equation}
其中R(t)为硬件和软件的滤波,a将平方电场转换为测量的光电子计数。电压在一系列时间点kTL(k为整数)与本地振荡器(LO)光梳同步数字化。将方程(8)代入方程(9),得到:
\\begin{equation} V_k' = V'\\bigl(t = kT_L\\bigr) = a\\int e^{-i\\Delta\\varphi} \\sum_{n,m} R(\\tau') A_L^{*}\\bigl((k-m)T_L – \\tau'\\bigr) A_S\\bigl(kT_L – nT_S – \\tau'\\bigr) d\\tau'. \\end{equation}
根据有效时间teff=kΔT重写(注意TL=TS+ΔT),并进行变量替换r≡n−m、p≡k−m、τ=τ′−kTL+pTS,经过一些整理后得到:\\begin{equation} V'\\bigl(t_{eff}\\bigr) = e^{-i\\Delta\\varphi} \\sum_{r=0}^{r=T/T_{frame}} V\\bigl(t_{eff} – rT_S\\bigr), \\tag{10} \\end{equation}
其中单个项(干涉图)为:\\begin{equation} V(t) = \\int S(t') A_s\\bigl(t – t'\\bigr) dt' \\equiv S(t) \\otimes A_s(t), \\tag{11} \\end{equation}采样函数为\\begin{equation} S(t) = a\\sum_p R\\bigl(pT_S + t\\bigr) A_L^{*}\\bigl(p\\Delta T – t\\bigr). \\end{equation}。
方程(10)简单描述了一系列拼接的干涉图。如果进行傅里叶变换,可得到参考文献 [6] 中的射频光梳。然而,直接相加单个干涉图在噪声抑制方面同样有效。在同步采样的假设下,干涉图之间无相位偏移,且时间点网格teff=kΔT与有效时间偏移Ts对齐,因此计算平均干涉图<v(teff)>时无需插值。此后,本文省略括号,并令teff→t。在假设 3 下,ΔT足够短,使得pΔT可视为连续变量(pΔT→τ),因此S(t)的求和可根据方程(6)重写为\\begin{equation} S(t) \\approx a\\Delta T^{-1} \\int R\\bigl(K\\tau + t\\bigr) A_L^{*}\\bigl(\\tau – t\\bigr) d\\tau \\end{equation}。通过变量替换,得到:\\begin{equation} S(t) = a\\Delta T^{-1} R\\bigl[(K+1)t\\bigr] \\otimes A_L^{*}\\left[-\\left(\\frac{K+1}{K}\\right)t\\right]. \\tag{12} \\end{equation}
在K≫1和宽探测带宽的极限下,S(t)≈AL∗(−t)(与预期一致)。
从频域角度来看,在长脉冲序列的极限下,方程(8)也可表示为:
\\begin{equation} \\begin{aligned} E_S(t) &= e^{i\\varphi_S} e^{-i2\\pi v_0 t} \\sum_q \\tilde{A}_S\\bigl(qf_{rS}\\bigr) e^{-i2\\pi qf_{rS} t}, \\\\ E_L(t) &= e^{i\\varphi_S+\\Delta\\varphi} e^{-i2\\pi v_0 t} \\sum_p \\tilde{A}_L\\bigl(pf_{rL}\\bigr) e^{-i2\\pi pf_{rL} t}, \\end{aligned} \\tag{13} \\end{equation}
方程(9)给出\\begin{equation} V(t) = e^{i\\Delta\\varphi} \\sum_{p,q} \\int d\\tau \\int df\\,\\tilde{R}(f) e^{-i2\\pi f\\tau} \\tilde{A}_L^{*}\\bigl(pf_{rL}\\bigr) \\tilde{A}_S\\bigl(qf_{rS}\\bigr) e^{i2\\pi pf_{rL}(t-\\tau)} e^{-i2\\pi qf_{rS}(t-\\tau)}. \\end{equation}
令p=w+q并完成积分,得到:
\\begin{equation} V'(t) = e^{-i\\Delta\\varphi} a \\sum_{w,q} \\tilde{R}\\bigl(q\\Delta f_r – wf_{rL}\\bigr) \\tilde{A}_L^{*}\\bigl(qf_{rL} + wf_{rL}\\bigr) \\tilde{A}_S\\bigl(qf_{rS}\\bigr) e^{-i2\\pi q\\Delta f_r t} e^{i2\\pi wf_{rL} t}. \\tag{14} \\end{equation}
仅有w=0项保留,且q存在有限范围,因此:
\\begin{equation} V'(t) = e^{-i\\Delta\\varphi} a \\sum_{q=q_{\\min}}^{q=q_{\\max}} \\tilde{R}\\bigl(q\\Delta f_r\\bigr) \\tilde{A}_L^{*}\\bigl(qf_{rL}\\bigr) \\tilde{A}_S\\bigl(qf_{rS}\\bigr) e^{-i2\\pi q\\Delta f_r t}, \\tag{15} \\end{equation}
其傅里叶变换为:\\begin{equation} \\tilde{V}'(f) = e^{-i\\Delta\\varphi} a \\sum_{q=q_{\\min}}^{q=q_{\\max}} \\tilde{R}\\bigl(q\\Delta f_r\\bigr) \\tilde{A}_L^{*}\\bigl(qf_{rL}\\bigr) \\tilde{A}_S\\bigl(qf_{rS}\\bigr) \\delta\\bigl(f – q\\Delta f_r\\bigr), \\tag{16} \\end{equation}
即考虑探测器频率响应修正后的标准 “多外差” 结果:射频光梳中,qΔfr处的每个齿是相邻第q个光梳齿之间的拍频 [1,2,6]。根据光频v=(K+1)f重写,得到\\begin{equation} \\tilde{V}'(\\nu) = e^{-i\\Delta\\varphi} a\\,(K+1)^{-1} \\tilde{R}\\bigl(\\nu/(K+1)\\bigr) \\tilde{A}_L^{*}\\bigl(\\nu K/(K+1)\\bigr) \\tilde{A}_S(\\nu) \\sum_q \\delta\\bigl(\\nu – qf_{rS}\\bigr). \\end{equation}由于观测时间有限,delta 函数应替换为 sinc 函数;然而,由于在v=qfrS网格上采样,数值保持不变,因此:\\begin{equation} \\tilde{V}(\\nu) = e^{-i\\Delta\\varphi} \\tilde{S}(\\nu) \\tilde{A}_S(\\nu), \\tag{17} \\end{equation}其中:\\begin{equation} \\tilde{S}(\\nu) = \\frac{a}{K+1} \\tilde{R}\\left(\\frac{\\nu}{K+1}\\right) \\tilde{A}_L^{*}\\left(\\frac{K}{K+1}\\nu\\right), \\tag{18} \\end{equation}或方程(12)的变换。恢复v0(因此$A_{S(L)} \\to E_{S(L)}$),进行傅里叶变换,添加样品响应的影响和噪声项,得到:\\begin{equation} V(t) = S(t) \\otimes E_S(t) \\otimes H(t) + \\frac{n(t)}{\\sqrt{T_A \\Delta f_r}}, \\tag{19} \\end{equation}在K个时间点(间隔为ΔT,覆盖时间窗口Ts)处求值,其中n(t)为单个干涉图中的噪声,通过平均干涉图数量(等于TAΔfr)的平方根降低。干涉图的形状如图 1 所示,包含中心脉冲(振荡频率为∣vA−v0∣,宽度约为ΔvA−1)和自由感应衰减信号。如果n(t)的标准偏差为σ,则峰值时域信噪比为:\\begin{equation} (S/N)_t = \\sqrt{T_A \\Delta f_r} \\frac{V(0)}{\\sigma_t}. \\tag{20} \\end{equation}
在频域中,方程(19)的傅里叶变换为:\\begin{equation} \\tilde{V}(\\nu) = \\tilde{S}(\\nu) \\tilde{E}_S(\\nu) \\tilde{H}(\\nu) + \\frac{\\tilde{n}(\\nu)}{\\sqrt{T_A \\Delta f_r}}, \\tag{21} \\end{equation}在(K/2+1)个频率点(间隔为frS,覆盖带宽(2ΔT)−1,光频偏移为v0)处求值。任一正交分量的信噪比为:\\begin{equation} (S/N)_\\nu = \\sqrt{T_A \\Delta f_r} \\frac{\\tilde{V}(\\nu)}{\\sigma_\\nu}, \\tag{22} \\end{equation}其中噪声项$\\tilde{n}(\\nu)$的实部和虚部标准偏差相等(均为σv)。
该信噪比适用于方程(1)中的参考和信号。因此,归一化透射率或样品响应的噪声为:\\begin{equation} \\sigma_H = \\frac{2}{(S/N)_\\nu}, \\tag{23} \\end{equation}其中分子包含一个来自参考和信号对比的2因子,以及一个来自测量参考和信号必须花费相等时间的2因子。此时,探测器响应R(v)消去。下文假设带宽与奈奎斯特频率匹配(从而避免混叠噪声),但忽略R(v)。
3.2 加性白噪声源的贡献
本节推导方程(2)。每个干涉图中来自探测器噪声、散粒噪声和激光相对强度噪声(RIN)的加性、白色、高斯噪声的标准偏差为:\\begin{equation} \\sigma_t = \\sqrt{\\sigma_d^2 + \\eta n_S + \\eta n_{LO} + (RIN_S)\\bigl(f_r/2\\bigr)\\eta^2 n_L^2 + (RIN_L)\\bigl(f_r/2\\bigr)\\eta^2 n_S^2}. \\tag{24} \\end{equation}
第一项为探测器和数字化仪噪声贡献σd(单位为光子计数);第二项和第三项为散粒噪声,其中nS(LO)为滤波带ΔvA内每个源光梳(本地振荡器(LO)光梳)脉冲的光子数。散粒噪声项在技术上是乘性的(随中心脉冲变化),但如果中心脉冲比干涉图短,则忽略这种变化。最后两项源于激光器的额外相对强度噪声(RIN),本文假设其源于附加放大自发辐射(ASE)场。由于相对强度噪声(RIN)为白噪声,因此每个脉冲的光子数变化δns满足$ \\left(\\frac{\\delta n_S}{n_S}\\right)^2 = RIN_S \\left(\\frac{f_r}{2}\\right)$(因为相对强度噪声(RIN)为单边噪声)。通过平衡探测,可抵消每个激光器的这种相对强度噪声(RIN);然而,本地振荡器(LO)光梳脉冲与源光梳放大自发辐射(ASE)分量之间的拍频噪声,以及反之亦然的拍频噪声无法抵消,从而导致方程(24)中的第四项和第五项。无平衡探测时,相对强度噪声(RIN)贡献加倍。干涉图的峰值信号为$V(0) = 2\\eta\\sqrt{n_S n_{LO}} = 2\\eta\\sqrt{\\gamma n_S}$,因此方程(20)变为:\\begin{equation} (S/N)_t = \\sqrt{T_A \\Delta f_r} \\frac{2\\eta n_S}{\\sqrt{\\gamma^{-1} \\sigma_d^2 + 2c_\\gamma \\eta n_S + c_\\gamma b\\,(RIN)\\,f_r \\eta^2 n_S^2 + 4D^{-2} \\eta^2 n_S^2}}, \\tag{25} \\end{equation}
其中$c_\\gamma = (1+\\gamma)/(2\\gamma),\\quad c_{\\gamma^2} = (1+\\gamma^2)/(2\\gamma)$(假设RINL=RINS=RIN),引入参数b=1(2)分别表示平衡(非平衡)光学探测。分母中的最后一项用于考虑探测中的实验动态范围限制,将单个干涉图的信噪比限制为D。括号内的分数为单个干涉图的信噪比;当γ=1时,在散粒噪声限制下等于![]() ,在动态范围限制下等于D(可由光电探测、放大或数字化仪设定)。
,在动态范围限制下等于D(可由光电探测、放大或数字化仪设定)。
在白噪声假设下,频域信噪比为![]() ,其中括号表示测量光谱的平均值 [16]。对高斯信号光谱中心半高宽(FWHM)内的分子取平均值(记为
,其中括号表示测量光谱的平均值 [16]。对高斯信号光谱中心半高宽(FWHM)内的分子取平均值(记为![]() ),得到$\\langle|\\tilde{V}(\\nu)|\\rangle_{\\Delta\\nu_A} \\big/ \\langle|\\tilde{V}(\\nu)|\\rangle = K f_r \\operatorname{erf}\\bigl(\\sqrt{\\ln(2)}\\bigr) \\big/ \\bigl(2\\Delta\\nu_A\\bigr) \\sim 0.4 K f_r / \\Delta\\nu_A$(当ΔvA≪(2ΔT)−1时,可避免混叠)。令$P_{cA} \\equiv h\\nu f_r n_S$,则频域中的方程(25)变为:
),得到$\\langle|\\tilde{V}(\\nu)|\\rangle_{\\Delta\\nu_A} \\big/ \\langle|\\tilde{V}(\\nu)|\\rangle = K f_r \\operatorname{erf}\\bigl(\\sqrt{\\ln(2)}\\bigr) \\big/ \\bigl(2\\Delta\\nu_A\\bigr) \\sim 0.4 K f_r / \\Delta\\nu_A$(当ΔvA≪(2ΔT)−1时,可避免混叠)。令$P_{cA} \\equiv h\\nu f_r n_S$,则频域中的方程(25)变为:
\\begin{equation} (S/N)_\\nu = 0.8 \\frac{\\sqrt{T_A}}{M_A} \\frac{2 P_{cA}}{\\sqrt{\\gamma^{-1} NEP^2 + 4c_\\gamma \\eta^{-1} h\\nu P_{cA} + 2b c_{\\gamma^2}\\,(RIN)\\,P_{cA}^2 + 8D^{-2} f_r^{-1} P_{cA}^2}}, \\tag{26} \\end{equation}
其中使用frS≈frL≈fr、MA=ΔvA/fr,以及等式$\\sigma_d \\eta^{-1} h\\nu = NEP / \\sqrt{2 f_r}$。假设整个光谱上实现相同的信噪比(即相对强度噪声(RIN)和功率在光谱上是平坦的),并考虑光谱重建,将TA=T/F、M=MA(Δv/ΔvA)、Pc=Pc,A(Δv/ΔvA)和ΔvA=Δv/(FNd)代入方程(26),再将结果代入方程(23),得到:\\begin{equation} \\sigma_H = \\frac{M}{\\sqrt{T}} \\left\\{ \\frac{1}{0.8} \\sqrt{ \\left( \\frac{NEP}{P_c} \\right)^2 \\gamma^{-1} F + c_\\gamma \\left( \\frac{4h\\nu}{\\eta P_c} \\right) \\frac{1}{N_d} + 2b c_{\\gamma^2} \\frac{RIN}{F N_d^2} + \\frac{8}{D^2 f_r F N_d^2} } \\right\\}. \\tag{27} \\end{equation}
通过平滑(即时域切趾)可将该不确定度改善至分辨率res。在这种情况下,重新定义M=Δv/vres(保留其作为分辨元素数量的定义),并乘以$\\sqrt{\\varepsilon} = \\sqrt{\\nu_{res} / f_r}$,最终得到方程(2)。
完全在频域中推导相同的表达式(27)更为简便。为简化计算,令γ=1,因此源光梳和本地振荡器(LO)光梳的每个齿功率Ptooth相同。两个齿之间的均方根信号幅度为$\\sqrt{2} \\eta P_{\\text{tooth}}$(对应于它们的光频差处的射频频率)。白噪声功率为$\\bigl[ \\eta^2 NEP^2 + 4\\eta h\\nu P_{cA} + 2b\\eta^2 P_{cA}^2 \\,(RIN) \\bigr] B$,其中第一项为探测器噪声,第二项为两个源的散粒噪声,第三项为两个源的相对强度噪声(RIN)。注意,散粒噪声和相对强度噪声(RIN)均由总光梳功率PcA给出。有效带宽为B=1/(2TA)。该随机噪声功率对幅度和相位噪声的贡献相等,因此:\\begin{equation} (S/N)_\\nu = \\frac{2\\sqrt{T_A} P_{\\text{tooth}}}{\\sqrt{NEP^2 + 4\\eta^{-1} h\\nu P_{cA} + 2b P_{cA}^2 RIN}}. \\tag{28} \\end{equation}
在假设的高斯光谱半高宽(FWHM)内取平均,光梳齿功率为Ptooth=0.8PcA/MA,恢复γ并引入D后,方程(28)与方程(26)完全相同。
3.3 对已知气体的灵敏度
密度为ρ、长度为L的弱吸收气体的时域响应为H(t)=sinc(πtΔv)⊗[δ(t)+ρLF(t)],其中 sinc 项反映带宽Δv上的仪器响应,方括号内的项为样品响应(由函数F(t)表征)。本文采用标准匹配滤波方法,定义截止时间t0,屏蔽掉t0之前的点,以避免中心脉冲上的乘性噪声。柱密度ρL的不确定度为$\\sigma_{pL} = \\sigma_{t,R} \\big/ \\sqrt{\\sum_{\\substack{t_i=T_S\\\\t_i>t_0}} F^2(t_i)} = \\sigma_H \\sqrt{2\\nu_{res}} \\big/ \\sqrt{\\int_{t_0}^{T_S} \\big|F^2(t)\\big|^2}$,其中σ$_{t,R}$=σ$_H$/M是光谱重建时域干涉图的标准偏差(见图 1)。对于沃伊特轮廓,vj处的单条吸收线(积分线强度为Sj)的时域响应为$F_j(t) = S_j \\theta(t) e^{-2\\pi i \\nu_j t} e^{-\\pi^2 \\Delta \\nu_D^2 t^2/(4\\ln 2) – \\pi \\Delta \\nu_{Lor,j} t}$,其中ΔvD为多普勒半高宽(FWHM),ΔvLor为洛伦兹半高宽(FWHM),θ(t)为亥维赛阶跃函数(该时域信号恰好是自由感应衰减)。本文假设碰撞展宽线($\\Delta \\nu_{Lor} > \\Delta \\nu_D$)。如果$t_0 \\ll \\Delta \\nu_{Lor,j}^{-1} \\ll f_r^{-1}$,则积分限为 0 和∞,$\\sigma_{pL} = \\sigma_H \\sqrt{2\\nu_{res}} \\big/ \\sqrt{\\sum_j S_j^2 \\bigl(2\\pi\\Delta\\nu_{Lor,j}\\bigr)^{-1}}$(求和项覆盖所有观测线)。对于洛伦兹线,特定线的峰值吸收为αj=2ρSj/(πΔvLor,j)。为将其重写为更常规的形式,令σρL=(ρL)min(最小可探测柱密度),然后通过特定参考线(记为j=0)对其进行缩放,得到归一化到参考线的有效最小吸收$\\bigl(\\alpha_0 L\\bigr)_{\\min}^{\\text{effective}} \\equiv 2 S_0 \\bigl(\\pi\\Delta\\nu_{Lor}\\bigr)^{-1} \\bigl(\\rho L\\bigr)_{\\min}$,即方程(4)。
3.4 光梳间残余相位噪声导致的乘性噪声
由于无法完全消除残余噪声,光梳脉冲之间会存在残余幅度、定时和相位抖动。载波相位噪声通常占主导地位,因为它最难控制,且特别是在锁定或监测带宽之外,光梳会存在一些残余高频相位变化 [20]。因此,方程(19)的第一项修改为$V(t) \\to e^{i\\delta\\varphi(Kt)} V(t)$,其中指数项描述了相对载波相位抖动随实验室时间的变化。快速相位变化尤其棘手(见第 2.5 节)。如果相位变化较小(<1 弧度),则会在方程(19)中添加乘性噪声n(t)=iV(t)δφ(t)。根据广义方程(22)和(23),协方差为:$\\begin{equation} \\sigma_{H,mult}^2(\\nu,\\nu') = \\left( \\frac{4}{T_A \\Delta f_r} \\right) \\frac{\\langle \\tilde{n}(\\nu) \\tilde{n}^*(\\nu') \\rangle}{\\tilde{V}(\\nu) \\tilde{V}^*(\\nu')}. \\tag{29} \\end{equation}$其中$$\\tilde{n}(\\nu) = \\tilde{\\varphi}\\bigl((\\nu-\\nu_0)/K\\bigr) \\otimes i\\tilde{V}(\\nu)。假设脉冲间相位方差为$\\sigma_{\\varphi,\\,fast}^2$,$ \\langle \\tilde{\\varphi}(f) \\tilde{\\varphi}^*(f') \\rangle = \\sigma_{\\varphi,\\,fast}^2 f_r^{-1} \\delta(f-f')$,且滤波器轮廓为高斯型$V(\\nu) = \\exp\\bigl[-4\\ln(2)\\,(\\nu-\\nu_A)^2 / \\Delta\\nu_A^2\\bigr]$,因此:\\begin{equation} \\sigma_{H,mult}(\\nu,\\nu') \\approx \\left( \\frac{2\\pi}{\\ln(2)} \\right)^{1/4} \\sqrt{\\frac{\\Delta\\nu_A}{T_A f_r^2}} \\sigma_{\\varphi,\\,fast} e^{4\\ln(2)\\,(\\bar{\\nu}-\\nu_A)^2/\\Delta\\nu_A^2}, \\tag{30} \\end{equation}其中vˉ=(v+v′)/2。正如预期的那样,噪声在光谱边缘呈指数增长,因为白相位噪声会产生宽带噪声,而信号则呈指数下降。在中心位置v=v′=vA,噪声仅为方程(30)中指数项的前置因子。将数据限制在半高宽(FWHM)范围内,即vA−ΔvA/2<v<vA+ΔvA/2。通过相位校正可去除相关噪声,剩余非相关噪声为方程(30)前置因子的根号3倍。代入T=FTA和Δv=NdFΔvA,得到方程(5)。对于有效时间的相对抖动δt或相对分数幅度噪声δa,可通过替换n(t)=(δt)dV(t)/dt或n(t)=(δa)V(t)进行类似推导。
致谢
本研究得到美国国土安全部和国家标准与技术研究院的支持。作者感谢法布里齐奥・乔尔杰塔、亚历克斯・佐洛特以及匿名评审人的有益评论。
 网硕互联帮助中心
网硕互联帮助中心

![[Linux]学习笔记系列 -- [drivers][tty]sysrq-网硕互联帮助中心](https://www.wsisp.com/helps/wp-content/uploads/2026/02/20260207073525-6986eb3d0c39c-220x150.png)

评论前必须登录!
注册