TDOA（到达时间差）的GDOP和CRLB计算的MATLAB例程，论文复现，附参考文献。GDOP：几何精度因子&CRLB：克拉美罗下界

程序用于三维 TDOA（Time Difference of Arrival）定位系统中几何精度的定量分析。通过构建多基站 TDOA 测量模型，计算目标在不同空间位置处的 GDOP（Geometric Dilution of Precision） 以及对应的 CRLB（Cramér–Rao Lower Bound），并以固定高度切片的形式，在二维平面上绘制 GDOP 与 CRLB 的三维曲面图及等高线地形图，用于评估基站布局对定位精度的影响。

代码根据参考文献编写，非AI生成，仅供学习与交流，禁止翻卖

文章目录

• 代码介绍
• • 基站与误差建模
  • GDOP 与 CRLB 计算方法
  • 可视化与结果分析方式
• 运行结果
• MATLAB源代码

代码介绍

基站与误差建模

程序采用 九基站正方形阵列布局，基站分布于同一高度平面，其中一个为主基站，其余为参考基站。该布局具有较好的对称性，常用于 TDOA 定位精度分析与对比研究。

在误差建模方面，同时考虑了两类误差来源：

GDOP 与 CRLB 计算方法

对每一个目标点位置，首先构建 TDOA 观测方程的几何矩阵。该矩阵由目标点到各基站的视线方向向量差构成，反映了系统在该位置处的几何可观测性。

• GDOP 通过几何矩阵的正规方程计算得到，用于描述定位误差对测量噪声的放大程度，GDOP 越小，几何构型越优。
• CRLB 在 GDOP 的基础上进一步引入测量噪声与基站误差协方差，给出位置估计误差的理论下界，能够更真实地反映系统的极限定位精度。

可视化与结果分析方式

程序在给定高度 ( z ) 条件下，对目标在二维平面内进行网格遍历，分别绘制：

• GDOP 的三维曲面图与等高线地形图；
• CRLB 的三维曲面图与等高线地形图。

运行结果

根据论文里面的锚点设置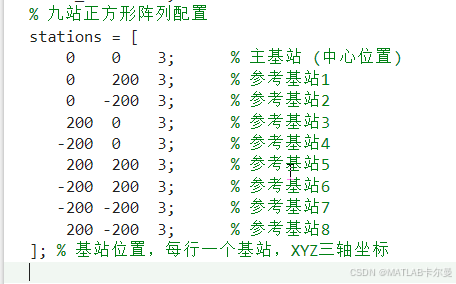： 得到的GDOP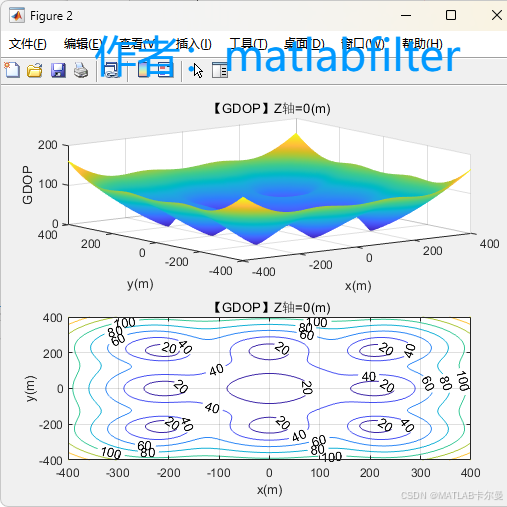： CRLB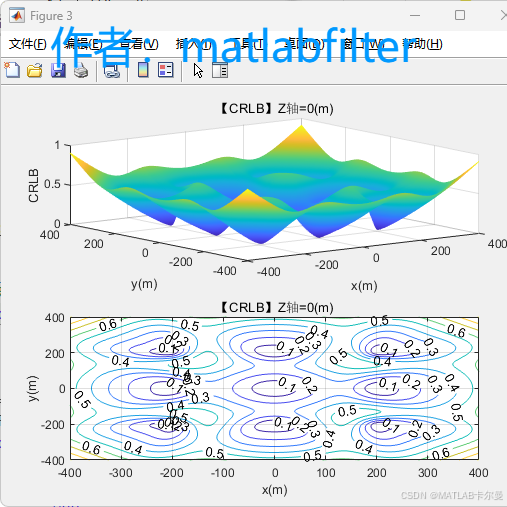： 锚点位置示意图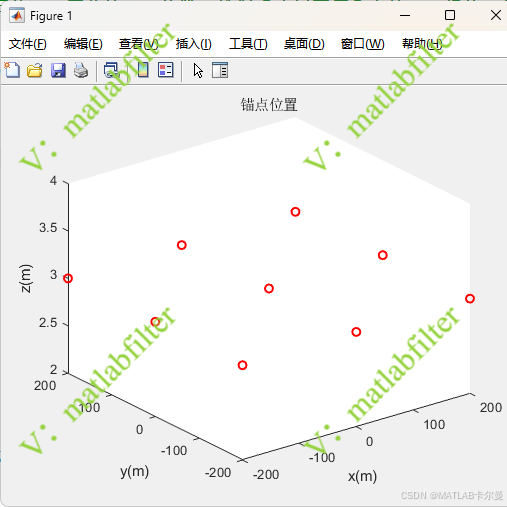： 基站修改为非共面以后，结果如下：

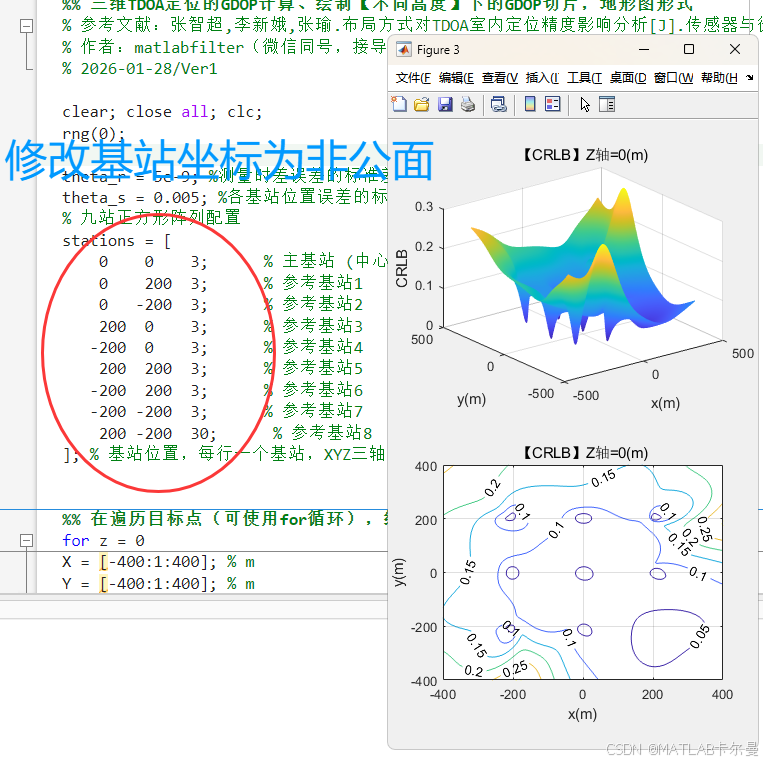
MATLAB源代码

部分代码如下：

%% 三维TDOA定位的GDOP计算、绘制【不同高度】下的GDOP切片，地形图形式
% 参考文献：张智超,李新娥,张瑜.布局方式对TDOA室内定位精度影响分析[J].传感器与微系统,2023,42(09):61-64
% 作者：matlabfilter
% 2026-01-28/Ver1

clear; close all; clc;
rng(0);

theta_r = 5e-9; %测量时差误差的标准差
theta_s = 0.005; %各基站位置误差的标准差
% 九站正方形阵列配置
stations = [
0 0 3; % 主基站 (中心位置)
0 200 3; % 参考基站1
0 –200 3; % 参考基站2
200 0 3; % 参考基站3
–200 0 3; % 参考基站4
200 200 3; % 参考基站5
–200 200 3; % 参考基站6
–200 –200 3; % 参考基站7
200 –200 3; % 参考基站8
]; % 基站位置，每行一个基站，XYZ三轴坐标

%% 在遍历目标点（可使用for循环），绘制不同目标点的GPOD
for z = 0
X = [–400:1:400]; % m
Y = [–400:1:400]; % m
G=zeros(length(X),length(Y),'double');
CRLB = zeros(length(X),length(Y),'double');
for i = 1:length(X)
for j = 1:length(Y)
[G(i,j),CRLB(i,j)] = gdop_1(stations,[X(i),Y(j),z],theta_r,theta_s);
end
end
G = real(G);
CRLB = real(CRLB);
%

完整代码： https://download.csdn.net/download/callmeup/92631169

参考文献：张智超,李新娥,张瑜.布局方式对TDOA室内定位精度影响分析[J].传感器与微系统,2023,42(09):61-64

如需帮助，或有导航、定位滤波相关的代码定制需求，请点击下方卡片联系作者