注:本文为 “PN 结” 相关合辑。 图片清晰度受引文原图所限。 略作重排,未整理去重。 如有内容异常,请看原文。
PN 结的电容效应
Ethan Jiang 原创 2020-02-12 11:56:17
本文对 PN 结的单向导电特性的频率依赖性进行解析,说明该特性并非在所有工况下成立,当信号频率达到特定值时,PN 结将失去单向导电特性。同时深入分析 PN 结在正向偏置、反向偏置两种电压条件下的工作原理,阐述不同偏置下的电流形成过程,并探究电容效应对 PN 结导电性的影响规律。
PN 结单向导电性的工况限定
PN 结并非在任何情况下均具备单向导电性,答案为:否 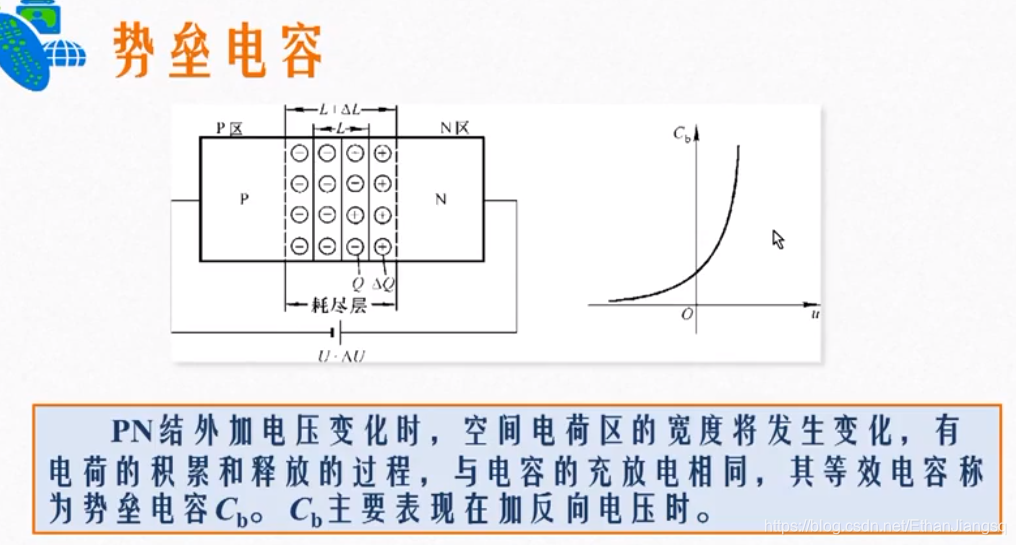
势垒电容随反向偏置电压的增加而减小,随正向偏置电压的增加而增大。
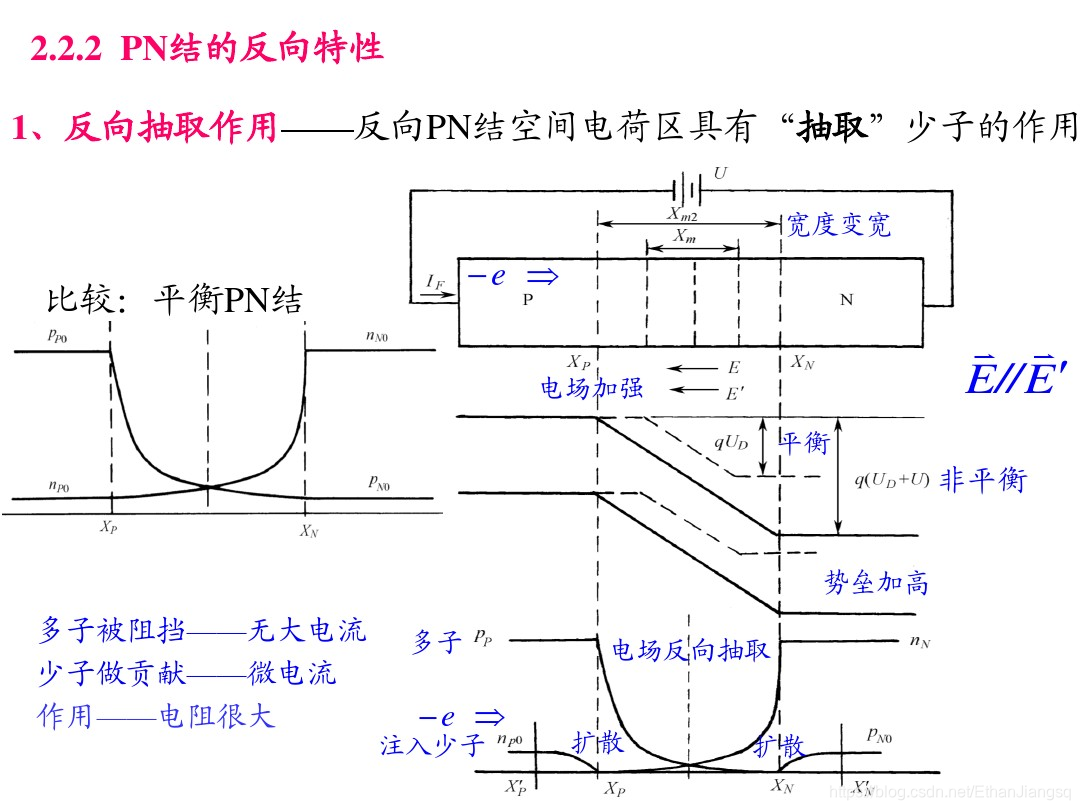
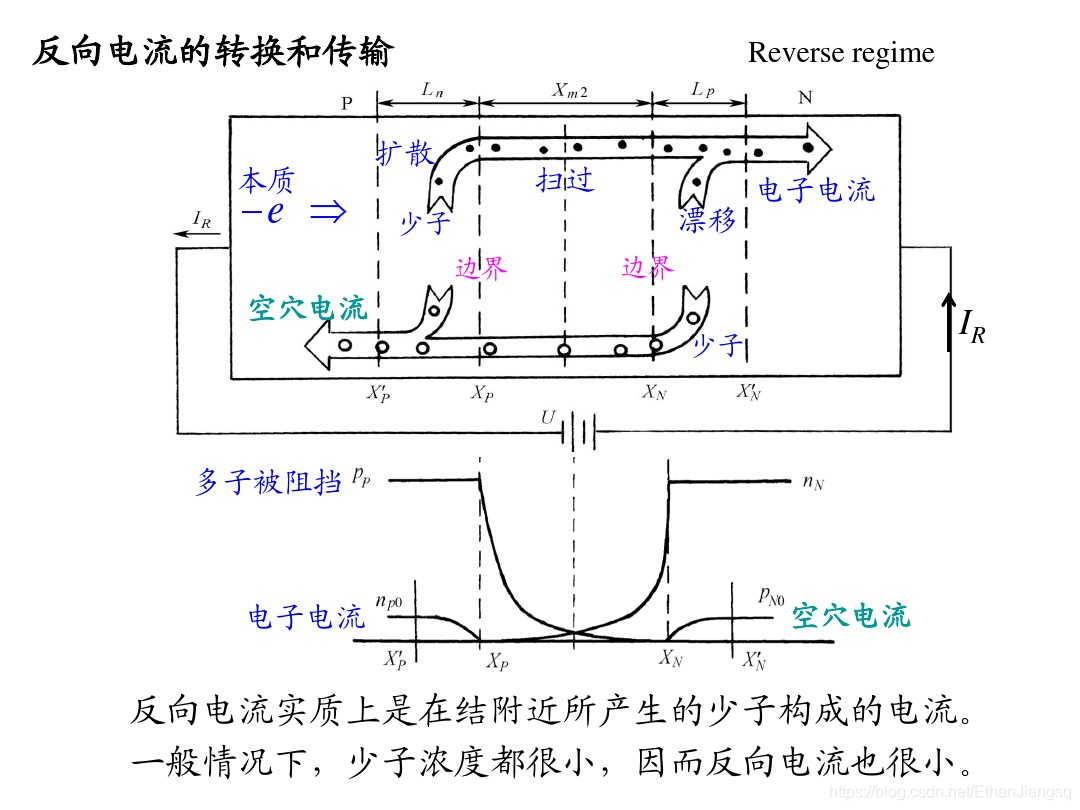
PN 结的反向特性
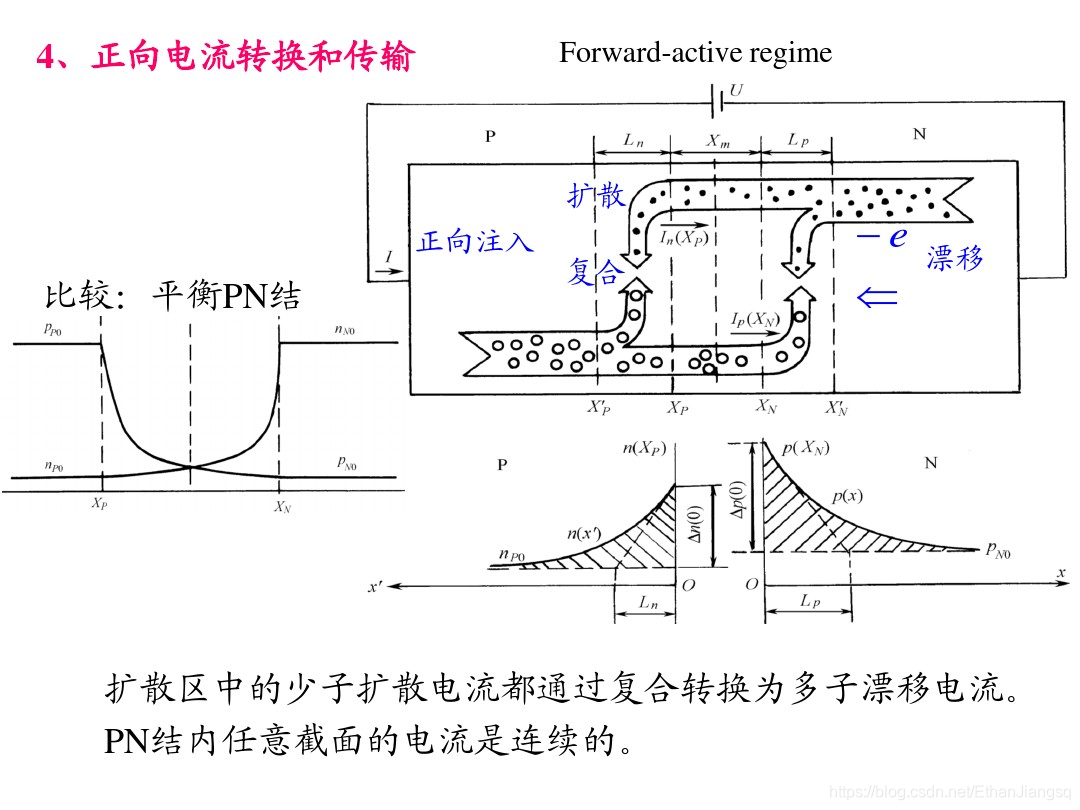
热平衡状态下,N 区的少子空穴、P 区的少子自由电子的浓度分布如下图所示: 
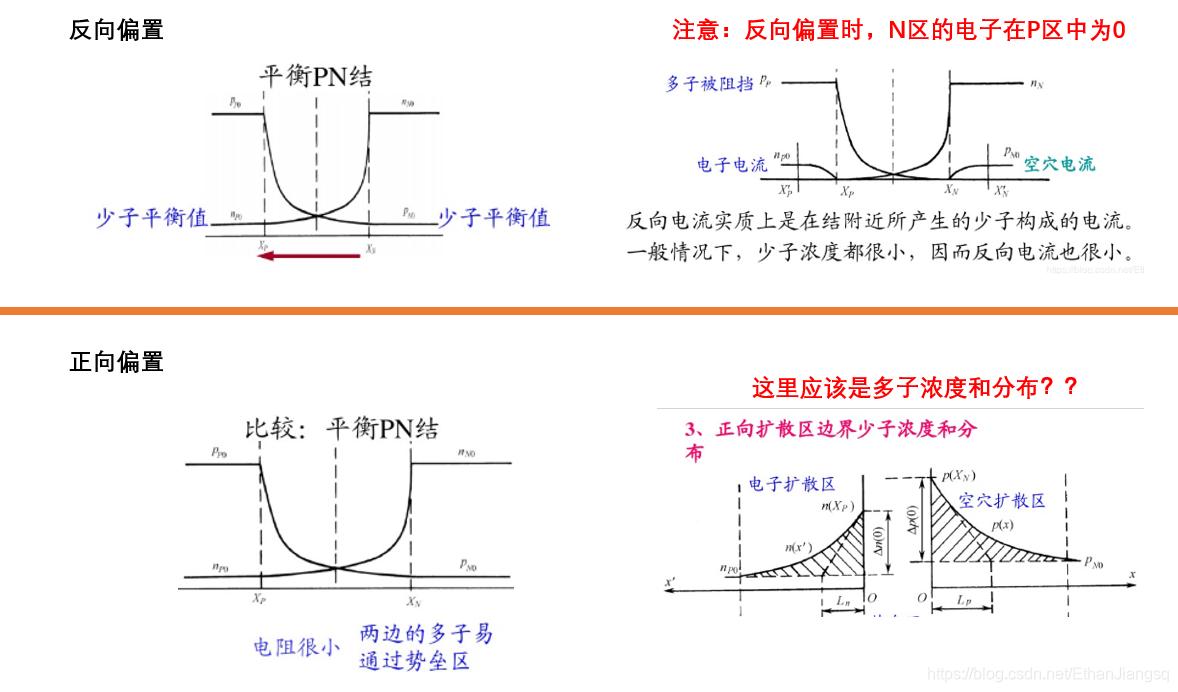
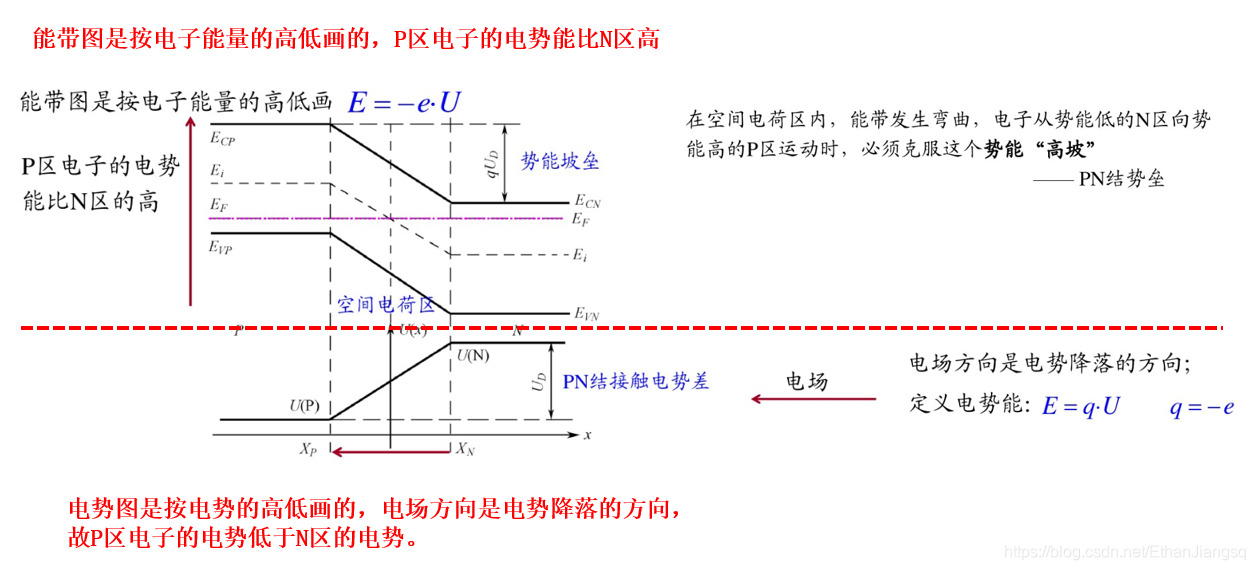
当 P 区接负极、N 区接正极时,PN 结处于反向偏置状态。外电场与 PN 结内建电场同向,对载流子形成反向抽取作用,耗尽区宽度增大,N 区与 P 区间的电势差形成的能垒高度提升。此时载流子的输运以少子的漂移运动为主,漂移运动的强度大于扩散运动,形成的反向电流数值极小;多子因能垒阻挡无法进入耗尽区,PN 结呈现高电阻特性。耗尽区内强电场的作用使载流子无法停留,且耗尽区边界处的少子浓度低于热平衡状态下的平均浓度。 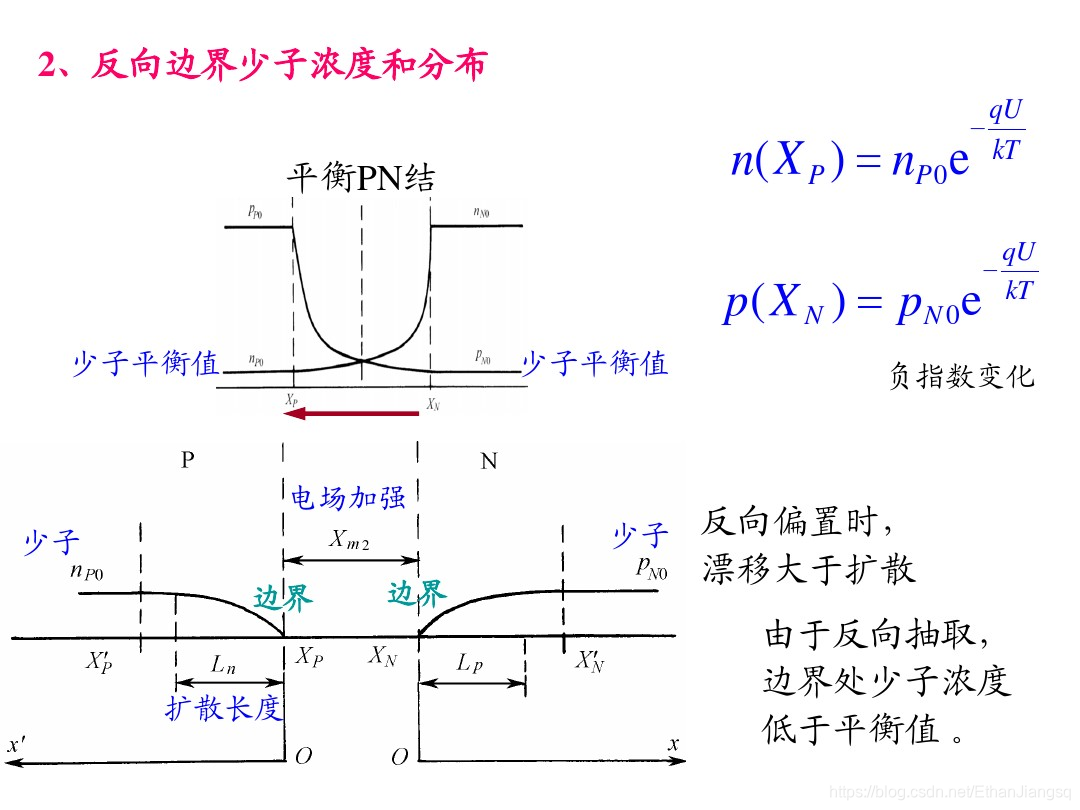
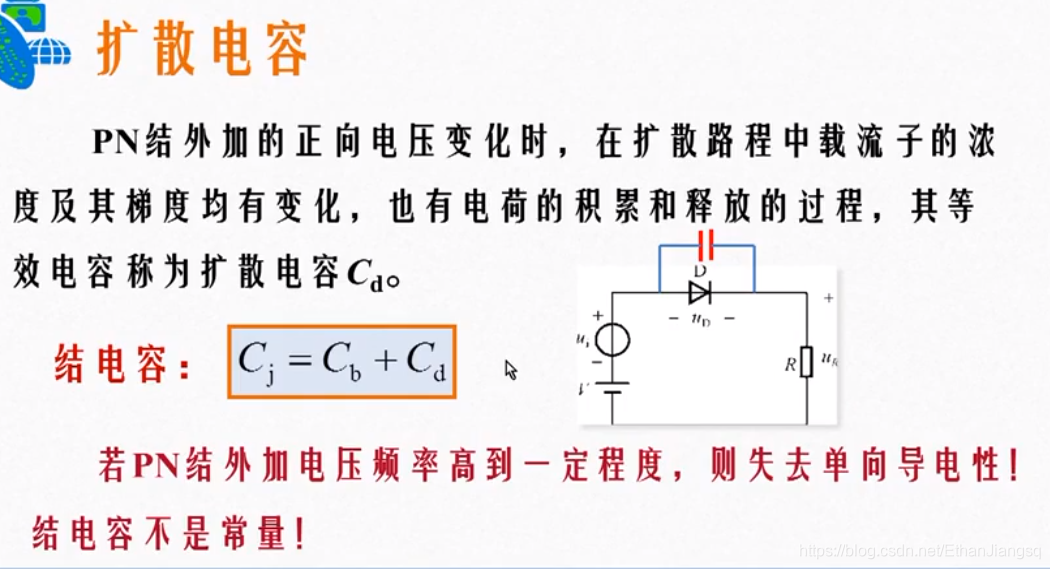
PN 结的电容效应可等效为在二极管两端并联一个电容,该电容的容值为结电容,结电容为势垒电容与扩散电容的代数和。当输入信号的频率升高至特定值时,结电容的容抗降低至可忽略的程度,动态信号将全部施加于 PN 结的等效电阻上,结电容两端无压降,此时 PN 结的单向导电特性消失,等效为结电容被短路。
PN 结存在一极限频率,当外加电压的频率超过该极限频率时,PN 结将丧失单向导电特性。 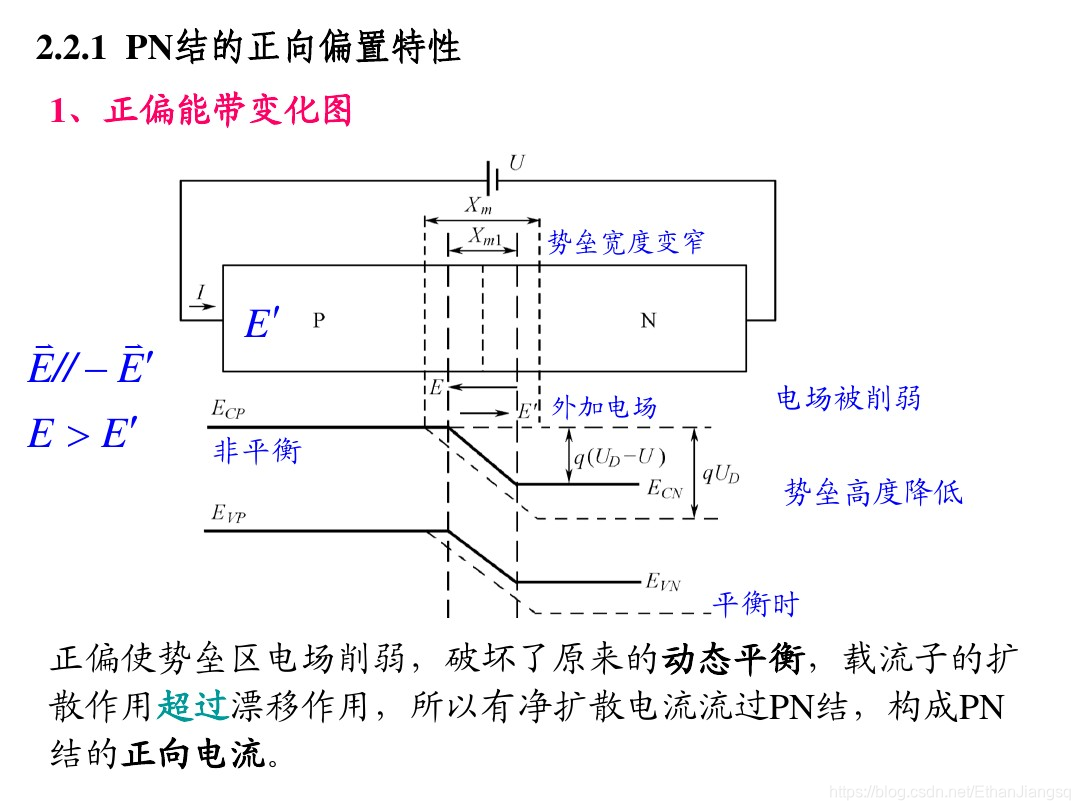
当 P 区(阳极)接正极、N 区(阴极)接负极时,PN 结处于正向偏置状态。外电场与内建电场反向,能垒高度降低,载流子的输运以多子的扩散运动为主,扩散运动的强度大于漂移运动,形成的正向电流数值较大。 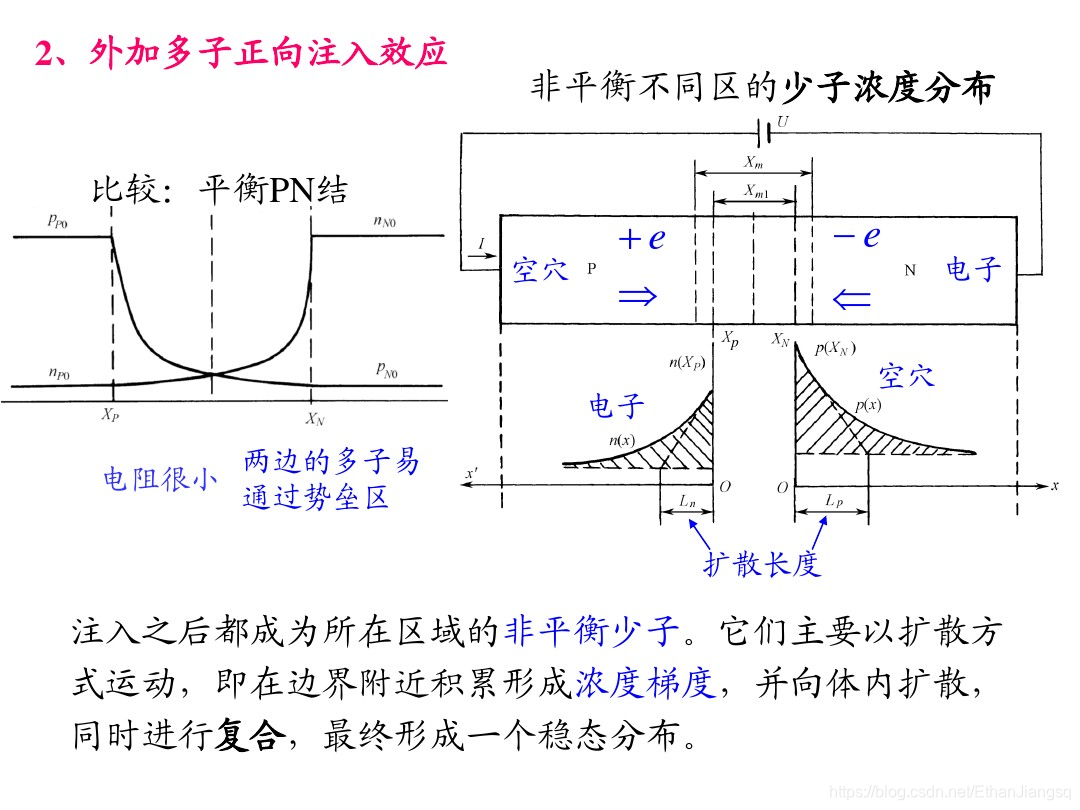
偏置状态对比
势垒电容与 PN 结偏置电压的变化规律
势垒电容的物理根源在于 PN 结耗尽层(即空间电荷区)中电荷数量随外加电压变化而产生的电容效应。其容值
C
b
C_b
Cb 与耗尽层宽度
W
W
W 成反比,即
C
b
=
ε
s
A
W
∝
1
W
,
C_b = \\frac{\\varepsilon_s A}{W} \\propto \\frac{1}{W},
Cb=WεsA∝W1,
其中
ε
s
\\varepsilon_s
εs 为半导体介电常数,
A
A
A 为结面积。因此,势垒电容的变化由耗尽层宽度的改变决定,二者呈反向关系。随着 PN 结偏置电压的调整,势垒电容的具体变化规律如下:
W
W
W 增大,势垒电容
C
b
C_b
Cb 减小;反之,当反向偏置电压减小时,耗尽层变窄,
C
b
C_b
Cb 增大。
W
W
W 减小,势垒电容
C
b
C_b
Cb 增大;反之,当正向偏置电压减小时,耗尽层展宽,
C
b
C_b
Cb 减小。
势垒电容的定量表达式为:
C
b
=
C
b
0
(
1
−
V
V
b
i
)
m
,
C_b = \\frac{C_{b0}}{\\left(1 – \\frac{V}{V_{bi}}\\right)^m},
Cb=(1−VbiV)mCb0,
其中各参数定义如下:
-
C
b
0
C_{b0}
Cb0:PN 结在零偏置(V
=
0
V = 0
V=0)时的势垒电容; -
V
V
V:外加偏置电压(注意:此处V
V
V 为代数量,反向偏置时V
<
0
V < 0
V<0,正向偏置时V
>
0
V > 0
V>0); -
V
b
i
V_{bi}
Vbi:PN 结的内建电势(硅基 PN 结约为 0.6–0.8 V,与掺杂浓度和温度相关); -
m
m
m:梯度系数,取决于掺杂分布——突变结m
≈
1
2
m \\approx \\tfrac{1}{2}
m≈21,线性缓变结m
≈
1
3
m \\approx \\tfrac{1}{3}
m≈31,超突变结m
>
1
2
m > \\tfrac{1}{2}
m>21。
对于反向偏置(
V
<
0
V < 0
V<0),令
∣
V
R
∣
=
−
V
|V_R| = -V
∣VR∣=−V,则上式可改写为:
C
b
=
C
b
0
(
1
+
∣
V
R
∣
V
b
i
)
m
.
C_b = \\frac{C_{b0}}{\\left(1 + \\frac{|V_R|}{V_{bi}}\\right)^m}.
Cb=(1+Vbi∣VR∣)mCb0.
可见,随着反向偏压
∣
V
R
∣
|V_R|
∣VR∣ 增大,分母增大,
C
b
C_b
Cb 单调减小。这一定量结果与前述定性分析完全一致,也符合 PN 结势垒电容的 C–V 特性曲线。
适用范围与极限
需要特别指出,上述公式主要适用于反向偏置及弱正向偏置(
V
≲
0.7
V
b
i
V \\lesssim 0.7V_{bi}
V≲0.7Vbi)的情况。在强正向偏置下(
V
→
V
b
i
V \\to V_{bi}
V→Vbi):
- 耗尽层近似失效,公式分母趋近于零,预测
C
b
→
∞
C_b \\to \\infty
Cb→∞,与物理实际不符; - 此时扩散电容
C
d
C_d
Cd(由少子电荷存储效应产生)开始占绝对主导,其值通常比势垒电容大10
2
∼
10
3
10^2 \\sim 10^3
102∼103 倍,且随正向电流近似指数增长; - 因此,在正偏导通状态下,总结电容
C
j
=
C
b
+
C
d
≈
C
d
C_j = C_b + C_d \\approx C_d
Cj=Cb+Cd≈Cd,势垒电容的压控特性不再具有实际意义。
工程应用中的**变容二极管(Varactor)**正是利用反向偏置下势垒电容的压控特性实现调谐功能,此时器件始终工作在反偏区以避免扩散电容的干扰。
常见错误辨析
需特别指出:势垒电容随反向电压的增大而减小 是唯一正确的结论。常见的错误认知主要有两类: (1)混淆势垒电容与扩散电容的电压依赖特性——扩散电容在正向偏置下占主导且随正向电压增大而显著增大,但该特性不适用于势垒电容; (2)忽视公式中电压
V
V
V 的符号约定,误将反向电压代入正值,导致对公式的错误解读。
物理本质总结
本质上,势垒电容的变化源于耗尽层中空间电荷量随电压的调整。此行为可类比于平行板电容器:电容与极板间距成反比,而耗尽层宽度
W
W
W 正好等效于"极板间距"。因此,
W
W
W 增大 →
C
b
C_b
Cb 减小;
W
W
W 减小 →
C
b
C_b
Cb 增大,这一规律是势垒电容的固有特性。
半导体器件物理:PN 结击穿机制与结电容特性
GuiStar_李什么恩 原创,修订于 2023-03-01 19:35:22
1. PN 结的击穿与电容效应
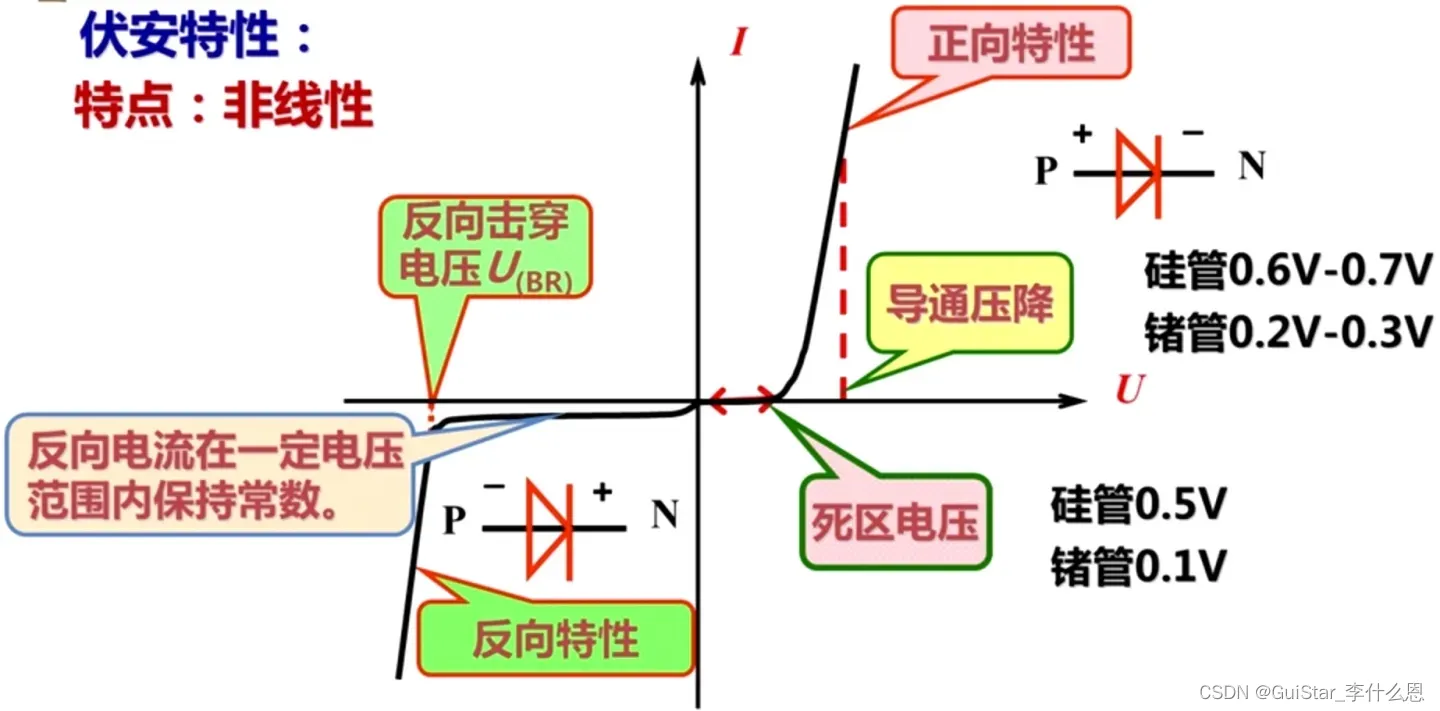
预备知识:二极管伏安特性
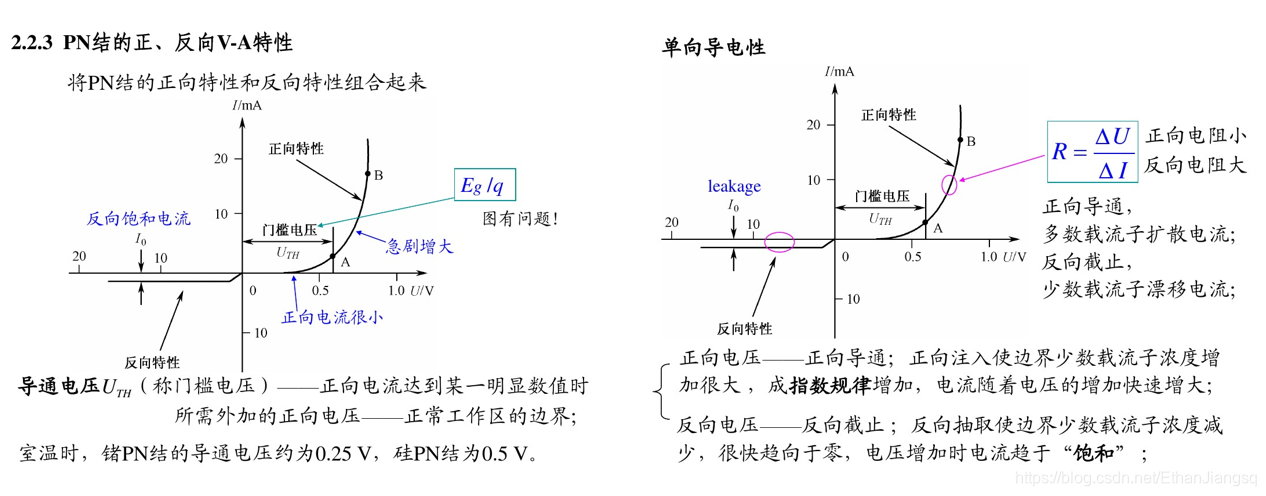
PN 结的电流-电压特性遵循肖克利方程,其典型的伏安特性曲线如图 1 所示,该曲线直观反映了 PN 结在不同外加电压下的导电特性,是分析击穿机制与电容效应的基础。
2. 掺杂浓度对耗尽层特性的影响
2.1 热力学平衡原理
从热力学角度分析,孤立系统总是朝着熵增加的方向演化,即系统会自发地从非平衡态向平衡态过渡,削弱其内部的非均匀性。这一熵增原理在半导体物理中的具体体现为,载流子具有从高浓度区域向低浓度区域扩散的趋势,最终趋于均匀的浓度分布,以削弱浓度的局部不均匀性。
以温度分布为例,热量总是从高温区域流向低温区域,直至系统达到热平衡状态,削弱温度的局部不均匀性;同理,载流子浓度也遵循这一规律,通过扩散运动削弱浓度的局部差异,这是 PN 结耗尽层形成的重要热力学基础。
2.2 掺杂浓度与耗尽层宽度的关系
设
N
A
N_A
NA 为受主杂质浓度(P 区),
N
D
N_D
ND 为施主杂质浓度(N 区)。根据泊松方程与电荷中性条件,耗尽层宽度
W
W
W 满足:
W
=
x
p
+
x
n
=
2
ε
s
(
V
b
i
−
V
)
q
(
1
N
A
+
1
N
D
)
W = x_p + x_n = \\sqrt{\\frac{2\\varepsilon_s(V_{bi}-V)}{q}\\left(\\frac{1}{N_A}+\\frac{1}{N_D}\\right)}
W=xp+xn=q2εs(Vbi−V)(NA1+ND1)
其中
ε
s
\\varepsilon_s
εs 为半导体介电常数,
V
b
i
V_{bi}
Vbi 为内建电势,
V
V
V 为外加电压,
q
q
q 为电子电荷量;注:外加电压
V
V
V 符号规则为正偏取正、反偏取负,反向偏压时
V
b
i
−
V
V_{bi}-V
Vbi−V 增大,耗尽层宽度变宽。
由上式及熵增原理的浓度扩散特性可知:
耗尽层宽度与掺杂浓度成反比:当
N
A
N_A
NA 或
N
D
N_D
ND 增大时,
W
W
W 减小。这是因为高掺杂浓度下,多子浓度较高,为削弱浓度局部不均匀性,更多多子通过扩散运动在耗尽层形成更高浓度的空间电荷,无需较宽的耗尽层即可实现电荷平衡,从而压缩了空间电荷区的范围。
空间电荷密度与掺杂浓度成正比:耗尽层内的电离杂质浓度直接等于掺杂浓度,因此高掺杂导致更高的空间电荷密度,满足
∣
Q
∣
=
q
N
A
x
p
=
q
N
D
x
n
|Q| = qN_A x_p = qN_D x_n
∣Q∣=qNAxp=qNDxn。从浓度均匀化趋势来看,高掺杂浓度可通过提高空间电荷密度来削弱浓度局部性,进一步验证了这一关系。
3. PN 结的击穿机制
3.1 雪崩击穿(Avalanche Breakdown)
当反向偏压
V
R
V_R
VR 增大时,耗尽层宽度增加,内部电场强度
E
\\mathcal{E}
E 增强。在此强电场作用下,漂移通过耗尽层的载流子(主要为少数载流子,内建电场对多子起阻碍作用,对少子起加速作用)获得足够动能,与晶格原子发生碰撞电离(impact ionization),产生电子-空穴对。
新生成的电子-空穴对在电场加速下继续发生碰撞电离,引发链式反应,形成载流子的倍增效应(multiplication)。当倍增因子
M
M
M 趋于无穷时,反向电流急剧增大,定义此时发生雪崩击穿。
击穿电压
V
B
R
V_{BR}
VBR 与掺杂浓度的经验关系为:
V
B
R
∝
1
N
0.75
V_{BR} \\propto \\frac{1}{N^{0.75}}
VBR∝N0.751
因此,雪崩击穿通常发生在低掺杂浓度的 PN 结中,此时耗尽层较宽,载流子有足够的加速距离获得足够能量以引发碰撞电离,满足链式反应的发生条件。
3.2 齐纳击穿(Zener Breakdown)
当掺杂浓度较高(通常
≥
10
17
c
m
−
3
\\ge10^{17} \\,\\mathrm{cm}^{-3}
≥1017cm−3,高掺杂时
>
10
18
c
m
−
3
>10^{18} \\,\\mathrm{cm}^{-3}
>1018cm−3)时,耗尽层宽度很窄(
<
10
n
m
<10 \\,\\mathrm{nm}
<10nm),即使较小的反向电压也能建立极强的电场(
>
10
6
V
/
c
m
>10^6 \\,\\mathrm{V/cm}
>106V/cm,即
>
10
8
V
/
m
>10^8 \\,\\mathrm{V/m}
>108V/m)。
在此强场作用下,直接破坏耗尽层中中性原子的共价键(场致电离),或使价带电子通过量子隧穿效应直接穿越禁带进入导带,产生大量电子-空穴对,导致反向电流急剧增大,该机制称为齐纳击穿或隧穿击穿。
齐纳击穿电压与掺杂浓度的关系表现为:随掺杂浓度增加,击穿电压降低。这是因为掺杂浓度越高,耗尽层越窄,所需反向电压越小即可建立起引发齐纳击穿的强电场。
3.3 两种击穿机制的比较
两种击穿机制均属于 PN 结反向击穿现象,在实际器件中可能同时存在,仅因掺杂浓度不同而表现出不同的主导机制。二者的具体特征对比如下表所示:
| 物理机制 | 碰撞电离与载流子倍增(链式反应) | 量子隧穿或强场致电离(共价键破坏) |
| 掺杂浓度 | 低(
< 10 17
c m − 3 <10^{17} \\,\\mathrm{cm}^{-3} <1017cm−3,典型值 < 10 16
c m − 3 <10^{16} \\,\\mathrm{cm}^{-3} <1016cm−3) |
高(
≥ 10 17
c m − 3 \\ge10^{17} \\,\\mathrm{cm}^{-3} ≥1017cm−3) |
| 耗尽层宽度 | 宽 | 窄 |
| 温度系数 | 正(正温度系数) | 负(负温度系数) |
| 击穿电压 | 高(通常
> 6 V >6 \\,\\mathrm{V} >6V) |
低(通常
< 6 V <6 \\,\\mathrm{V} <6V) |
对于硅 PN 结,当击穿电压
V
B
R
<
4.5
V
V_{BR} < 4.5 \\,\\mathrm{V}
VBR<4.5V 时以齐纳击穿为主;当
V
B
R
>
6.5
V
V_{BR} > 6.5 \\,\\mathrm{V}
VBR>6.5V 时以雪崩击穿为主;中间区域为两种机制的混合区。
4. PN 结的电容特性
PN 结的电容效应由势垒电容
C
j
C_j
Cj(结电容)和扩散电容
C
d
C_d
Cd 两部分组成,二者源于不同的物理机制,在不同偏置条件下表现出不同的主导作用,共同决定 PN 结的高频特性。
4.1 势垒电容(Barrier Capacitance)
势垒电容源于耗尽层内空间电荷随外加电压的变化。耗尽层中主要为不可移动的电离杂质电荷,当外加电压变化时,耗尽层宽度随之改变,空间电荷总量也相应变化,这一充放电过程等效为电容效应,根据定义其电容值为:
C
j
=
∣
d
Q
d
V
∣
=
ε
s
A
W
C_j = \\left|\\frac{dQ}{dV}\\right| = \\frac{\\varepsilon_s A}{W}
Cj=
dVdQ
=WεsA
其中
A
A
A 为结面积,
W
W
W 为耗尽层宽度。
对于突变结,势垒电容与偏压的关系为:
C
j
=
C
j
0
(
1
−
V
V
b
i
)
m
C_j = \\frac{C_{j0}}{\\left(1-\\frac{V}{V_{bi}}\\right)^m}
Cj=(1−VbiV)mCj0
其中
C
j
0
C_{j0}
Cj0 为零偏压时的结电容,
m
m
m 为梯度系数(突变结
m
=
1
/
2
m=1/2
m=1/2,线性缓变结
m
=
1
/
3
m=1/3
m=1/3)。
特性分析:
-
反偏时,
W
W
W 随
∣
V
R
∣
|V_R|
∣VR∣ 增大而增宽,空间电荷总量变化率减小,
C
j
C_j
Cj 随之减小;
-
正偏时,
W
W
W 变窄,
C
j
C_j
Cj 增大,但此时扩散电容占主导地位,势垒电容可忽略不计(仅中高电流正偏条件下适用)。
4.2 扩散电容(Diffusion Capacitance)
扩散电容源于正偏压下少子的注入与存储效应。PN 结正偏时,内建电场被削弱,大量少子越过势垒注入对方区域,在扩散区形成从耗尽层交界面指向远离交界面的递减浓度梯度。
该非平衡少子浓度梯度随外加正偏电压的变化而变化,电压增大时浓度梯度增大,扩散区存储的少子电荷总量也相应增加,这一充放电过程等效为电容效应,定义扩散电容为少子电荷随电压的变化率:
C
d
=
d
Q
p
d
V
=
τ
I
η
V
T
C_d = \\frac{dQ_p}{dV} = \\frac{\\tau I}{\\eta V_T}
Cd=dVdQp=ηVTτI
其中
τ
\\tau
τ 为少子寿命,
I
I
I 为正向电流,
V
T
=
k
T
/
q
V_T = kT/q
VT=kT/q 为热电压,
η
\\eta
η 为理想因子(
1
∼
2
1 \\sim 2
1∼2);该公式仅适用于低频小信号条件。
4.3 两种电容的比较
势垒电容与扩散电容的物理本质、特性存在显著差异,具体对比如下表所示:
| 偏置条件 | 主要存在于反偏及零偏,正偏时可忽略 | 主要存在于正偏,反偏时可忽略 |
| 物理来源 | 耗尽层宽度调制导致空间电荷变化 | 少子注入与存储导致少子电荷变化 |
| 数值范围 | 通常为 pF 量级 | 正偏时可至 nF 量级 |
| 频率特性 | 高频特性好,受频率影响小 | 受限于少子寿命,高频时失效 |
| 电压依赖性 |
C j ∝ ( V b i − V ) − m C_j \\propto (V_{bi}-V)^{-m} Cj∝(Vbi−V)−m(突变结 m = 1 / 2 m=1/2 m=1/2,线性缓变结 m = 1 / 3 m=1/3 m=1/3) |
C d ∝ exp ( q V / η k T ) C_d \\propto \\exp(qV/\\eta kT) Cd∝exp(qV/ηkT) |
PN 结的总电容为二者之和,即
C
t
o
t
a
l
=
C
j
+
C
d
C_{total} = C_j + C_d
Ctotal=Cj+Cd,实际应用中可根据工作点选择主导电容分量:反偏或低频小信号正偏条件下,
C
j
C_j
Cj 占主导;大电流正偏条件下,
C
d
C_d
Cd 显著增大并成为主要电容分量。
电场强度、电势以及 PN 结耗尽层宽度
猫的麦克斯韦 原创 2023-05-10 21:51:50 修订
1. 引言
本文系统阐述 PN 结耗尽层的基本物理特性,重点推导耗尽层内电场强度、静电电势的分布规律,并建立耗尽层宽度与掺杂浓度、内建电势之间的定量关系。分析基于突变结近似(abrupt junction approximation),即假设空间电荷区边界处杂质浓度发生理想突变,如图 1 所示。坐标系采用一维直角坐标系,冶金结界面位于
x
=
0
x = 0
x=0,P 区耗尽层边界位于
x
=
−
X
p
x = -X_p
x=−Xp,N 区耗尽层边界位于
x
=
+
X
n
x = +X_n
x=+Xn。
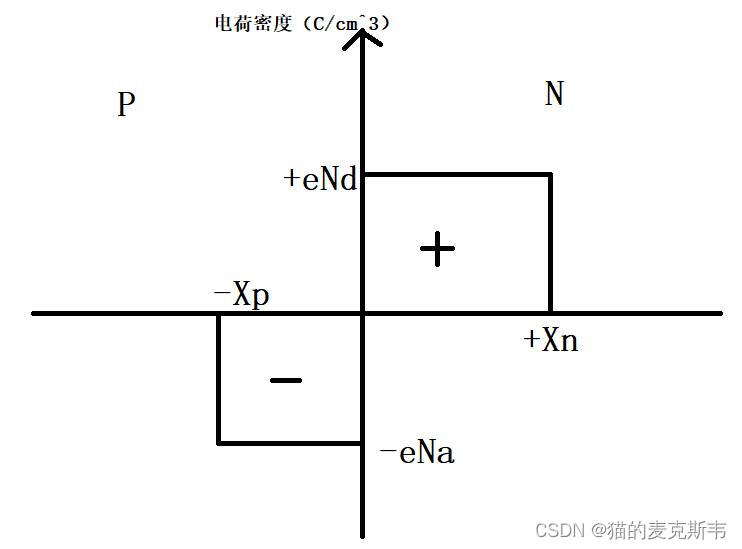
图 1 PN 结空间电荷区结构与坐标系示意图
2. 泊松方程与电荷分布
2.1 基本控制方程
半导体内静电势
ϕ
(
x
)
\\phi(x)
ϕ(x) 与空间电荷密度
ρ
(
x
)
\\rho(x)
ρ(x) 满足一维泊松方程:
d
2
ϕ
(
x
)
d
x
2
=
d
d
x
(
d
ϕ
(
x
)
d
x
)
⏟
=
−
E
(
x
)
=
d
d
x
[
−
E
(
x
)
]
=
−
d
E
(
x
)
d
x
=
−
ρ
(
x
)
ε
s
\\frac{\\mathrm{d}^{2}\\phi(x)}{\\mathrm{d}x^{2}} = \\frac{\\mathrm{d}}{\\mathrm{d}x}\\underbrace{\\left(\\frac{\\mathrm{d}\\phi(x)}{\\mathrm{d}x}\\right)}_{=-E(x)} = \\frac{\\mathrm{d}}{\\mathrm{d}x}[-E(x)] = -\\frac{\\mathrm{d}E(x)}{\\mathrm{d}x} = -\\frac{\\rho(x)}{\\varepsilon_s}
dx2d2ϕ(x)=dxd=−E(x)
(dxdϕ(x))=dxd[−E(x)]=−dxdE(x)=−εsρ(x)
其中,电势的二阶导数等于电场一阶导数的负值,
E
(
x
)
E(x)
E(x) 为电场强度,
ε
s
\\varepsilon_{s}
εs 为半导体材料的介电常数。
2.2 耗尽区电荷分布
在耗尽层近似(depletion approximation)下,耗尽区内载流子完全耗尽,空间电荷密度等于电离杂质电荷密度。因此,
ρ
(
x
)
\\rho(x)
ρ(x) 可用分段函数表示为:
ρ
(
x
)
=
{
−
q
N
A
,
−
X
p
<
x
<
0
+
q
N
D
,
0
<
x
<
X
n
\\rho(x) = \\begin{cases} -qN_{A}, & -X_{p} < x < 0 \\\\ +qN_{D}, & 0 < x < X_{n} \\end{cases}
ρ(x)={−qNA,+qND,−Xp<x<00<x<Xn
式中,
q
q
q 为电子电荷量的绝对值(
q
>
0
q > 0
q>0),
N
A
N_{A}
NA 和
N
D
N_{D}
ND 分别为 P 侧受主掺杂浓度与 N 侧施主掺杂浓度。
3. 电场强度分布
3.1 电场强度的推导
对泊松方程积分求解电场强度
E
(
x
)
E(x)
E(x)。根据热平衡条件,电中性区(
x
<
−
X
p
x < -X_{p}
x<−Xp 与
x
>
X
n
x > X_{n}
x>Xn)内电场强度为零。利用边界条件
E
(
−
X
p
)
=
0
E(-X_{p}) = 0
E(−Xp)=0 与
E
(
X
n
)
=
0
E(X_{n}) = 0
E(Xn)=0 确定积分常数,并保证冶金结处(
x
=
0
x = 0
x=0)电场强度连续,可得:
E
(
x
)
=
{
−
q
N
A
ε
s
(
x
+
X
p
)
,
−
X
p
≤
x
≤
0
−
q
N
D
ε
s
(
X
n
−
x
)
,
0
≤
x
≤
X
n
E(x) = \\begin{cases} -\\dfrac{qN_{A}}{\\varepsilon_{s}}(x + X_{p}), & -X_{p} \\leq x \\leq 0 \\\\[16pt] -\\dfrac{qN_{D}}{\\varepsilon_{s}}(X_{n} – x), & 0 \\leq x \\leq X_{n} \\end{cases}
E(x)=⎩
⎨
⎧−εsqNA(x+Xp),−εsqND(Xn−x),−Xp≤x≤00≤x≤Xn
3.2 电荷中性条件
由
E
(
0
−
)
=
E
(
0
+
)
E(0^{-}) = E(0^{+})
E(0−)=E(0+) 可得:
N
A
X
p
=
N
D
X
n
N_{A}X_{p} = N_{D}X_{n}
NAXp=NDXn
该式表明,P 区单位面积内受主离子总电荷量与 N 区单位面积内施主离子总电荷量相等,保证整个器件的空间电中性。冶金结界面处电场强度达到最大值
E
max
=
−
q
N
A
X
p
ε
s
=
−
q
N
D
X
n
ε
s
E_{\\max} = -\\dfrac{qN_{A}X_{p}}{\\varepsilon_{s}} = -\\dfrac{qN_{D}X_{n}}{\\varepsilon_{s}}
Emax=−εsqNAXp=−εsqNDXn
电场强度分布呈三角形,如图 2 所示。
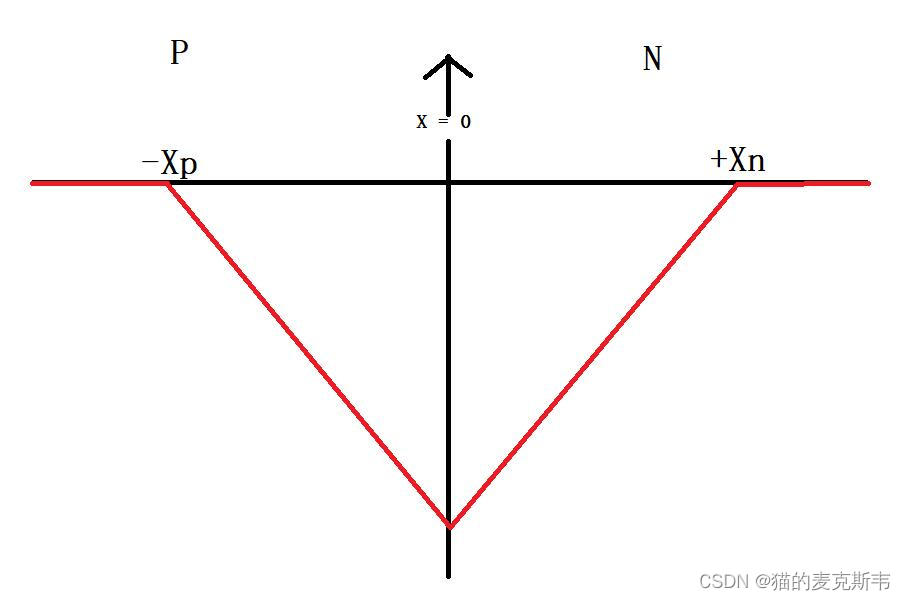
图 2 PN 结耗尽层电场强度分布示意图
4. 电势分布
4.1 静电势的积分求解
以 P 区电中性区边界为电势参考点,设
ϕ
(
−
X
p
)
=
0
\\phi(-X_{p}) = 0
ϕ(−Xp)=0。对电场强度
E
(
x
)
E(x)
E(x) 进行分段积分,并保证
x
=
0
x = 0
x=0 处电势连续,可得耗尽层内电势分布:
ϕ
(
x
)
=
{
q
N
A
2
ε
s
(
x
+
X
p
)
2
,
−
X
p
≤
x
≤
0
q
N
D
2
ε
s
(
X
n
x
−
x
2
2
)
+
q
N
A
2
ε
s
X
p
2
,
0
≤
x
≤
X
n
\\phi(x) = \\begin{cases} \\dfrac{qN_{A}}{2\\varepsilon_{s}}(x + X_{p})^{2}, &-X_{p} \\leq x \\leq 0 \\\\[16pt] \\dfrac{qN_{D}}{2\\varepsilon_{s}}\\left(X_{n}x – \\dfrac{x^{2}}{2}\\right) + \\dfrac{qN_{A}}{2\\varepsilon_{s}}X_{p}^{2}, & 0 \\leq x \\leq X_{n} \\end{cases}
ϕ(x)=⎩
⎨
⎧2εsqNA(x+Xp)2,2εsqND(Xnx−2x2)+2εsqNAXp2,−Xp≤x≤00≤x≤Xn
电势分布曲线如图 3 所示,呈抛物线型。
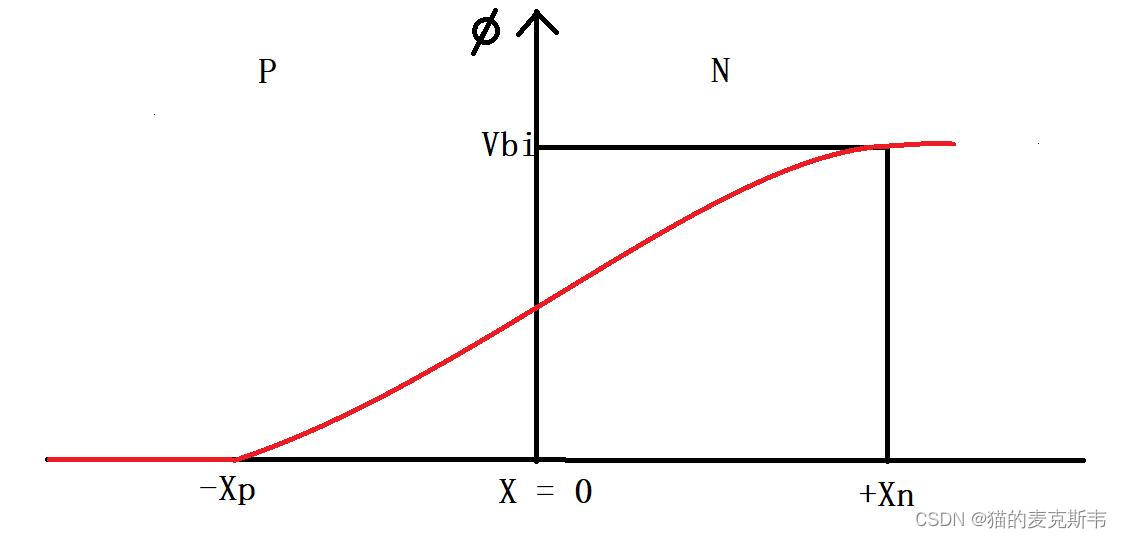
图 3 PN 结耗尽层电势分布示意图
在 P 型半导体一侧,耗尽层边界(与电中性区交界处)的电势被定义为零电位。 即:
ϕ
(
x
)
∣
x
=
−
X
p
=
0
\\phi(x)\\bigg|_{x=-X_p} = 0
ϕ(x)
x=−Xp=0
5. 内建电势与耗尽层宽度
5.1 内建电势表达式
x
=
X
n
x = X_{n}
x=Xn 处的电势绝对值即为 PN 结的内建电势(built-in potential)
V
b
i
V_{bi}
Vbi:
V
b
i
=
ϕ
(
X
n
)
=
q
2
ε
s
(
N
D
X
n
2
+
N
A
X
p
2
)
V_{bi} = \\phi(X_{n}) = \\dfrac{q}{2\\varepsilon_{s}}\\left(N_{D}X_{n}^{2} + N_{A}X_{p}^{2}\\right)
Vbi=ϕ(Xn)=2εsq(NDXn2+NAXp2)
5.2 耗尽层宽度公式
联立电荷中性条件
N
A
X
p
=
N
D
X
n
N_{A}X_{p} = N_{D}X_{n}
NAXp=NDXn 与内建电势表达式,可解得 N 侧与 P 侧耗尽层宽度分别为:
X
n
=
2
ε
s
V
b
i
q
⋅
N
A
N
D
(
N
A
+
N
D
)
X
p
=
2
ε
s
V
b
i
q
⋅
N
D
N
A
(
N
A
+
N
D
)
\\begin{aligned} X_{n} = \\sqrt{\\dfrac{2\\varepsilon_{s}V_{bi}}{q} \\cdot \\dfrac{N_{A}}{N_{D}(N_{A} + N_{D})}} \\\\ X_{p} = \\sqrt{\\dfrac{2\\varepsilon_{s}V_{bi}}{q} \\cdot \\dfrac{N_{D}}{N_{A}(N_{A} + N_{D})}} \\end{aligned}
Xn=q2εsVbi⋅ND(NA+ND)NA
Xp=q2εsVbi⋅NA(NA+ND)ND
耗尽层总宽度
W
=
X
n
+
X
p
W = X_{n} + X_{p}
W=Xn+Xp 可简化为:
W
=
2
ε
s
V
b
i
q
(
1
N
A
+
1
N
D
)
=
2
ε
s
V
b
i
q
⋅
N
A
+
N
D
N
A
N
D
W = \\sqrt{\\dfrac{2\\varepsilon_{s}V_{bi}}{q}\\left(\\dfrac{1}{N_{A}} + \\dfrac{1}{N_{D}}\\right)} = \\sqrt{\\dfrac{2\\varepsilon_{s}V_{bi}}{q} \\cdot \\dfrac{N_{A} + N_{D}}{N_{A}N_{D}}}
W=q2εsVbi(NA1+ND1)
=q2εsVbi⋅NANDNA+ND
6. 外加偏置电压对耗尽层的影响
6.1 偏置条件与边界设定
当 PN 结施加外部直流偏置电压
V
V
V 时,热平衡被打破。为统一分析,采用如下电压极性约定:
- 正向偏置(P 区接正、N 区接负):
V
>
0
V > 0
V>0 - 反向偏置(P 区接负、N 区接正):
V
<
0
V < 0
V<0
此时,耗尽层两侧的总电势差由平衡态的内建电势
V
b
i
V_{\\mathrm{bi}}
Vbi 变为有效势垒高度
(
V
b
i
−
V
)
(V_{\\mathrm{bi}} – V)
(Vbi−V)。
选取 P 区中性区边界
x
=
−
X
p
x = -X_p
x=−Xp 作为电势参考点,即
ϕ
(
−
X
p
)
=
0
\\phi(-X_p) = 0
ϕ(−Xp)=0。根据静电场连续性,冶金结界面
x
=
0
x = 0
x=0 处电势连续:
ϕ
(
0
−
)
=
ϕ
(
0
+
)
=
ϕ
(
0
)
.
\\phi(0^-) = \\phi(0^+) = \\phi(0).
ϕ(0−)=ϕ(0+)=ϕ(0).
6.2 耗尽层宽度的表达式
在耗尽层近似下,空间电荷区内电荷密度为常数:
- P 区:
ρ
=
−
q
N
A
\\rho = -q N_A
ρ=−qNA - N 区:
ρ
=
+
q
N
D
\\rho = +q N_D
ρ=+qND
其中
N
A
N_A
NA、
N
D
N_D
ND 为受主与施主掺杂浓度(取正值),
q
q
q 为基本电荷量。泊松方程在各区退化为分段线性的二阶微分方程。由于方程具有线性特性,非平衡态下的解可直接由平衡态形式推广,仅需将
V
b
i
V_{\\mathrm{bi}}
Vbi 替换为
(
V
b
i
−
V
)
(V_{\\mathrm{bi}} – V)
(Vbi−V)。
由此得到总耗尽层宽度:
W
(
V
)
=
2
ε
s
(
V
b
i
−
V
)
q
⋅
N
A
+
N
D
N
A
N
D
,
W(V) = \\sqrt{ \\frac{2\\varepsilon_s (V_{\\mathrm{bi}} – V)}{q} \\cdot \\frac{N_A + N_D}{N_A N_D} },
W(V)=q2εs(Vbi−V)⋅NANDNA+ND
, 其中
ε
s
\\varepsilon_s
εs 为半导体介电常数。
内建电势
V
b
i
V_{\\mathrm{bi}}
Vbi 由材料参数决定:
V
b
i
=
k
T
q
ln
!
(
N
A
N
D
n
i
2
)
,
V_{\\mathrm{bi}} = \\frac{kT}{q} \\ln!\\left( \\frac{N_A N_D}{n_i^2} \\right),
Vbi=qkTln!(ni2NAND), 其中
k
k
k 为玻尔兹曼常数,
T
T
T 为绝对温度,
n
i
n_i
ni 为本征载流子浓度。
6.3 分区宽度与物理行为
由耗尽区内电中性条件(P 区负电荷总量等于 N 区正电荷总量):
q
N
A
X
p
=
q
N
D
X
n
,
q N_A X_p = q N_D X_n,
qNAXp=qNDXn,
可得耗尽层在 P 区和 N 区的分区宽度:
X
p
(
V
)
=
N
D
N
A
+
N
D
,
W
(
V
)
,
X
n
(
V
)
=
N
A
N
A
+
N
D
,
W
(
V
)
.
X_p(V) = \\frac{N_D}{N_A + N_D} , W(V), \\quad X_n(V) = \\frac{N_A}{N_A + N_D} , W(V).
Xp(V)=NA+NDND,W(V),Xn(V)=NA+NDNA,W(V).
物理规律总结:
- 正向偏置(
V
>
0
V > 0
V>0): 有效势垒降低(V
b
i
−
V
<
V
b
i
V_{\\mathrm{bi}} – V < V_{\\mathrm{bi}}
Vbi−V<Vbi),耗尽层变窄(W
W
W 减小),多数载流子扩散增强,形成显著的正向电流。 - 反向偏置(
V
<
0
V < 0
V<0): 有效势垒升高(V
b
i
−
V
>
V
b
i
V_{\\mathrm{bi}} – V > V_{\\mathrm{bi}}
Vbi−V>Vbi),耗尽层展宽(W
W
W 增大),少数载流子漂移主导,产生几乎恒定的反向饱和电流。 - 非对称扩展特性: 耗尽层主要向低掺杂一侧延伸。若
N
A
≫
N
D
N_A \\gg N_D
NA≫ND,则X
n
≫
X
p
X_n \\gg X_p
Xn≫Xp,总宽度W
≈
X
n
W \\approx X_n
W≈Xn;反之若N
D
≫
N
A
N_D \\gg N_A
ND≫NA,则W
≈
X
p
W \\approx X_p
W≈Xp。
附录:积分运算基础
本文所涉及的积分运算基于以下基本公式:img 图 4 积分运算基础公式
一、幂函数与指数函数
| (1) |
∫ x a
d x = x a + 1 a + 1 + C \\displaystyle \\int x^{a}\\,\\mathrm{d}x = \\frac{x^{a+1}}{a+1} + C ∫xadx=a+1xa+1+C |
a ≠ − 1 a \\neq -1 a=−1 |
| (2) |
∫ 1 x
d x = ln ∣ x ∣ + C \\displaystyle \\int \\frac{1}{x}\\,\\mathrm{d}x = \\ln\\lvert x\\rvert + C ∫x1dx=ln∣x∣+C |
x ≠ 0 x \\neq 0 x=0 |
| (3) |
∫ a x
d x = a x ln a + C \\displaystyle \\int a^{x}\\,\\mathrm{d}x = \\frac{a^{x}}{\\ln a} + C ∫axdx=lnaax+C |
a > 0 , a ≠ 1 a > 0,\\; a \\neq 1 a>0,a=1 |
二、三角函数
| (4) |
∫ sin x d x = − cos x + C \\displaystyle \\int \\sin x\\,\\mathrm{d}x = -\\cos x + C ∫sinxdx=−cosx+C |
| (5) |
∫ cos x d x = sin x + C \\displaystyle \\int \\cos x\\,\\mathrm{d}x = \\sin x + C ∫cosxdx=sinx+C |
| (6) |
∫ tan x d x = − ln ∣ cos x ∣ + C = ln ∣ sec x ∣ + C \\displaystyle \\int \\tan x\\,\\mathrm{d}x = -\\ln\\lvert \\cos x\\rvert + C = \\ln\\lvert \\sec x\\rvert + C ∫tanxdx=−ln∣cosx∣+C=ln∣secx∣+C |
| (7) |
∫ cot x d x = ln ∣ sin x ∣ + C \\displaystyle \\int \\cot x\\,\\mathrm{d}x = \\ln\\lvert \\sin x\\rvert + C ∫cotxdx=ln∣sinx∣+C |
| (8) |
∫ sec x d x = ln ∣ sec x + tan x ∣ + C \\displaystyle \\int \\sec x\\,\\mathrm{d}x = \\ln\\lvert \\sec x + \\tan x\\rvert + C ∫secxdx=ln∣secx+tanx∣+C |
| (9) |
∫ csc x d x = ln ∣ csc x − cot x ∣ + C \\displaystyle \\int \\csc x\\,\\mathrm{d}x = \\ln\\lvert \\csc x – \\cot x\\rvert + C ∫cscxdx=ln∣cscx−cotx∣+C |
| (10) |
∫ sec 2 x d x = tan x + C \\displaystyle \\int \\sec^{2} x\\,\\mathrm{d}x = \\tan x + C ∫sec2xdx=tanx+C |
| (11) |
∫ csc 2 x d x = − cot x + C \\displaystyle \\int \\csc^{2} x\\,\\mathrm{d}x = -\\cot x + C ∫csc2xdx=−cotx+C |
三、反三角函数与代数函数
| (12) |
∫ d x 1 + x 2 = arctan x + C \\displaystyle \\int \\frac{\\mathrm{d}x}{1+x^{2}} = \\arctan x + C ∫1+x2dx=arctanx+C |
| (13) |
∫ d x x 2 + a 2 = 1 a arctan x a + C \\displaystyle \\int \\frac{\\mathrm{d}x}{x^{2}+a^{2}} = \\frac{1}{a}\\arctan\\frac{x}{a} + C ∫x2+a2dx=a1arctanax+C |
| (14) |
∫ d x x 2 − a 2 = 1 2 a ln ∣ x − a x + a ∣ + C = 1 2 a ln ∣ a − x a + x ∣ + C \\displaystyle \\int \\frac{\\mathrm{d}x}{x^{2}-a^{2}} = \\frac{1}{2a}\\ln\\left\\lvert \\frac{x-a}{x+a} \\right\\rvert + C = \\frac{1}{2a}\\ln\\left\\lvert \\frac{a-x}{a+x} \\right\\rvert + C ∫x2−a2dx=2a1ln x+ax−a +C=2a1ln a+xa−x +C |
| (15) |
∫ d x a 2 − x 2 = 1 2 a ln ∣ a + x a − x ∣ + C \\displaystyle \\int \\frac{\\mathrm{d}x}{a^{2}-x^{2}} = \\frac{1}{2a}\\ln\\left\\lvert \\frac{a+x}{a-x} \\right\\rvert + C ∫a2−x2dx=2a1ln a−xa+x +C |
| (16) |
∫ d x 1 − x 2 = arcsin x + C \\displaystyle \\int \\frac{\\mathrm{d}x}{\\sqrt{1-x^{2}}} = \\arcsin x + C ∫1−x2dx=arcsinx+C |
| (17) |
∫ d x a 2 − x 2 = arcsin x a + C \\displaystyle \\int \\frac{\\mathrm{d}x}{\\sqrt{a^{2}-x^{2}}} = \\arcsin\\frac{x}{a} + C ∫a2−x2dx=arcsinax+C |
四、含根式的积分(双曲/对数形式)
| (18) |
∫ d x x 2 ± a 2 = ln ∣ x + x 2 ± a 2 ∣ + C \\displaystyle \\int \\frac{\\mathrm{d}x}{\\sqrt{x^{2}\\pm a^{2}}} = \\ln\\left\\lvert x+\\sqrt{x^{2}\\pm a^{2}}\\right\\rvert + C ∫x2±a2dx=ln x+x2±a2 +C |
| (19) |
∫ a 2 − x 2
d x = x 2 a 2 − x 2 + a 2 2 arcsin x a + C \\displaystyle \\int \\sqrt{a^{2}-x^{2}}\\,\\mathrm{d}x = \\frac{x}{2}\\sqrt{a^{2}-x^{2}} + \\frac{a^{2}}{2}\\arcsin\\frac{x}{a} + C ∫a2−x2dx=2xa2−x2+2a2arcsinax+C |
| (20) |
∫ x 2 ± a 2
d x = x 2 x 2 ± a 2 ± a 2 2 ln ∣ x + x 2 ± a 2 ∣ + C \\displaystyle \\int \\sqrt{x^{2}\\pm a^{2}}\\,\\mathrm{d}x = \\frac{x}{2}\\sqrt{x^{2}\\pm a^{2}} \\pm \\frac{a^{2}}{2}\\ln\\left\\lvert x+\\sqrt{x^{2}\\pm a^{2}}\\right\\rvert + C ∫x2±a2dx=2xx2±a2±2a2ln x+x2±a2 +C |
PN 结的电容效应——势垒电容和扩散电容
小小石灰 原创 2024-07-17 11:22:52
PN 结在特定条件下呈现电容效应,根据电容效应的产生机理,可将 PN 结的结电容分为势垒电容与扩散电容两类,结电容为两类电容的代数和。
1 势垒电容
当 PN 结的外加反向偏置电压发生变化时,耗尽层的宽度将随之改变,耗尽层内的空间电荷数量随外加电压的变化而增减,该物理过程与电容器的充、放电过程等效,由此产生的电容效应称为势垒电容,记为
C
b
C_b
Cb。
势垒电容为非线性电容,其容值与 PN 结的结面积、耗尽层宽度、半导体的介电常数及外加偏置电压相关。对于制备完成的 PN 结,势垒电容与外加电压
u
u
u 的关系具有明确的变化规律。利用 PN 结反向偏置时势垒电容随外加电压变化的特性,可制备各类变容二极管。 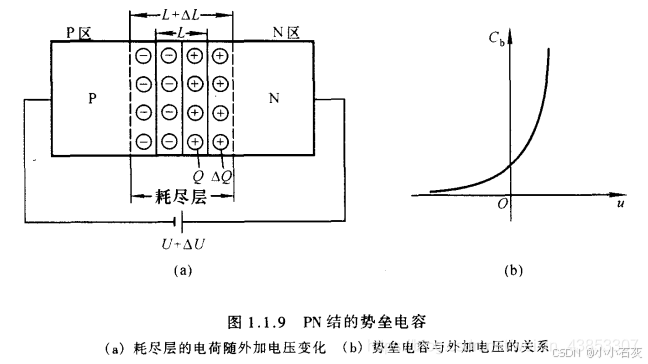
2 扩散电容
热平衡状态下,PN 结内的少子浓度为热平衡少子浓度;当 PN 结施加正向偏置电压时,从 P 区扩散至 N 区的空穴与从 N 区扩散至 P 区的自由电子为非平衡少子。
当外加正向偏置电压恒定,耗尽层交界面附近的非平衡少子浓度最高,随远离交界面,非平衡少子浓度逐渐降低并趋于 0,形成沿坐标方向的浓度梯度,非平衡少子的扩散运动形成扩散电流。当外加正向偏置电压增大时,非平衡少子的浓度与浓度梯度均增大,宏观表现为正向电流(扩散电流)增大;当外加正向偏置电压减小时,上述物理过程反向进行。
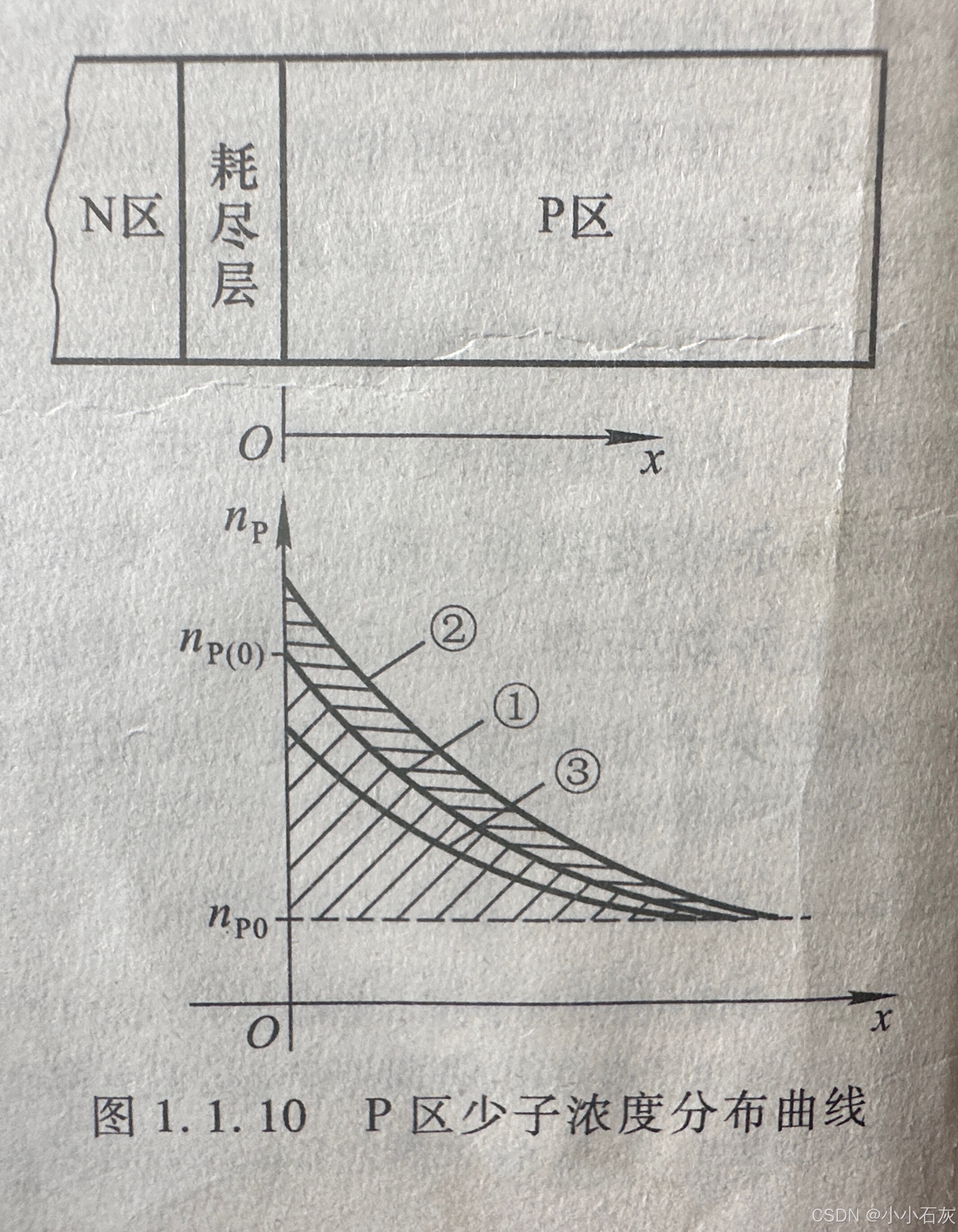
不同正向偏置电压下 P 区少子的浓度分布曲线中,曲线与
n
p
=
n
p
0
n_p=n_{p0}
np=np0 水平线间的面积代表扩散区域内非平衡少子的总数量。当外加电压增大时,非平衡少子的数量增多;当外加电压减小时,非平衡少子的数量减少。扩散区域内非平衡少子的电荷积累与释放过程与电容器的充、放电过程等效,由此产生的电容效应称为扩散电容,记为
C
d
C_d
Cd。
扩散电容同样为非线性电容,其容值与流过 PN 结的正向电流
i
i
i、温度的电压当量
U
T
U_T
UT 及非平衡少子的寿命
τ
\\tau
τ 相关。正向电流
i
i
i 越大、非平衡少子寿命
τ
\\tau
τ 越长、温度的电压当量
U
T
U_T
UT 越小,扩散电容
C
d
C_d
Cd 的容值越大。
PN 结的结电容
C
j
C_j
Cj 为势垒电容
C
b
C_b
Cb 与扩散电容
C
d
C_d
Cd 之和,即:
C
j
=
C
b
+
C
d
C_j=C_b+C_d
Cj=Cb+Cd
势垒电容与扩散电容的容值均较小,结面积较小的 PN 结结电容约为
1
pF
1\\ \\text{pF}
1 pF,结面积较大的 PN 结结电容为几十至几百皮法。对于低频信号,结电容呈现的容抗较大,其电容效应可忽略;仅当信号频率较高时,结电容的电容效应才需考虑。
via:
- PN 结的电容效应_pn 结电容-CSDN 博客 https://blog.csdn.net/ethanjiangsq/article/details/104272426
- 模电基础:一文彻底搞懂二极管击穿和结电容-CSDN博客 https://blog.csdn.net/hhhbdbfb/article/details/129287655
- 电场强度,电势以及 PN 结耗尽层宽度_pn 结耗尽区宽度计算公式-CSDN 博客 https://blog.csdn.net/weixin_44268068/article/details/130509763
- PN 结的电容效应——势垒电容和扩散电容-CSDN 博客 https://blog.csdn.net/weixin_65575911/article/details/140485773
 网硕互联帮助中心
网硕互联帮助中心






评论前必须登录!
注册