注:本文为 “逻辑演进与应用” 相关合辑。 英文引文,机翻未校。 中文引文,略作重排。 图片清晰度受引文原图所限。 如有内容异常,请看原文。
From Ancient Binary to Silicon Chips: Logic Through History
从古代二进制到硅芯片:逻辑学的发展历程
June 17, 2017 by Nexperia
Digital logic as we know it today required collaboration from thousands of people over thousands of years. 如今我们所熟知的数字逻辑,是数千年来无数人协作研究的成果。
Digital logic as we know it today required collaboration from thousands of people over thousands of years. 如今我们所熟知的数字逻辑,是数千年来无数人协作研究的成果。
Before electronic devices were ever created, mathematicians and philosophers were unknowingly creating the language of binary and laying the foundation for modern computing devices. These concepts were later applied to similar communication systems like Morse Code and the binary that we’re familiar with today. Mathematicians like George Boole and Charles Babbage applied these concepts to mechanical devices to automate them. While computing has a rich history, the logic gates that allow computers to function get less attention. 在电子设备诞生之前,数学家与哲学家便在无意间创立了二进制的表达体系,为现代计算设备的诞生奠定了基础。这些理论概念后来被应用于莫尔斯电码等同类通信系统,也成为了我们如今所熟知的二进制的雏形。乔治·布尔、查尔斯·巴贝奇等数学家将这些概念应用于机械设备,实现了设备的自动化运行。尽管计算机领域有着悠久且丰富的发展历史,但支撑计算机实现各项功能的逻辑门,却并未得到同等程度的关注。
Ancient Logic and Binary
古代逻辑学与二进制
In the 10th century in ancient China, a scholar named Shao Yong rearranged the hexagrams from the I Ching into a format similar to binary. Some scholars even suggest that the I Ching was Gottfried Leibniz’s inspiration for binary code. 公元 10 世纪的中国古代,学者邵雍将《易经》中的卦象重新排列,形成了类二进制的排布形式。部分学者甚至认为,《易经》正是戈特弗里德·莱布尼茨创造二进制编码的灵感来源。
 Ancient number systems compared with Leibniz’s binary, made by CounterComplex 古代记数系统与莱布尼茨二进制的对比图,由 CounterComplex 创作
Ancient number systems compared with Leibniz’s binary, made by CounterComplex 古代记数系统与莱布尼茨二进制的对比图,由 CounterComplex 创作
There were also truth tables in ancient Greece with YES and NO functioning like ON and OFF in the case of transistors. Leibniz most likely found inspiration from Greek mathematicians because their works were the most accessible for scholars in Europe during the 17th and 18th centuries. 古希腊时期便已出现真值表,其中的“是”与“否”逻辑,与晶体管中的“导通”和“关断”状态具有相通的作用原理。莱布尼茨的研究灵感大概率来源于古希腊数学家,因为在 17 至 18 世纪,古希腊数学家的著作是欧洲学者最易获取的研究资料。
There was also the small, remote Polynesian island of Mangareva which used a binary numeral system to help with mental arithmetic. Many ancient civilizations had numeric systems with similarities to binary as we know it today. Whether Leibniz was inspired by one of these other ancient systems will remain one of history’s mysteries. The study of ancient mathematics and binary is very interesting, but it also helps to temper one’s expectations and be prepared for misleading headlines and titles. 地处波利尼西亚的偏远小岛芒阿雷瓦,也曾使用一套二进制记数系统辅助心算。诸多古代文明所使用的记数方式,都与如今我们熟知的二进制存在相似性。莱布尼茨是否曾受这些古代记数体系的启发,这一问题至今仍是历史未解之谜。对古代数学与二进制的研究兼具趣味性,同时也能让研究者保持理性的研究视角,避免被误导性的标题与信息所影响。
From Mechanical to Digital Logic
从机械逻辑到数字逻辑
Although Gottfried Wilhelm Leibniz is credited with inventing binary as we know it today, the first logic based devices were created by Charles Babbage. His first Difference Engine was a mechanical calculator designed to tabulate polynomial equations and print the results on a roll of paper. 尽管戈特弗里德·威廉·莱布尼茨被公认为现代二进制的发明者,但首款基于逻辑原理的设备由查尔斯·巴贝奇研制。他设计的第一台差分机是一款机械计算器,可完成多项式方程的制表运算,并将运算结果打印在纸卷上。
In Babbage’s design, mechanical gears served the function of logic gates. He designed a second Difference Engine, also referred to as the Analytical Engine, but could never obtain funding to make it. His designs were later noticed in the 1980s and a fully functional model was finally created to his specifications. 在巴贝奇的设计中,机械齿轮承担了逻辑门的功能。他还设计了第二台差分机,也被称为分析机,但始终未能获得研发资金。直到 20 世纪 80 年代,他的设计方案才受到关注,人们最终依照其设计规格,制造出了一台可正常运行的样机。
The first common logic gates were electromagnetic relays, which were basically ON-OFF switches. The electromechanical relay was invented by Joseph Henry in 1835, but the brilliance of his invention was not realized until later when his relays were used in the telegraph. After the invention of the rotary dial in 1890, more complex relays with 10 positions were developed. 首款被广泛应用的逻辑门是电磁继电器,其本质为通断开关。电磁继电器由约瑟夫·亨利于 1835 年发明,但这一发明的价值在当时并未被发掘,直到后来被应用于电报系统,其优势才得以显现。1890 年旋转拨号盘发明后,可实现 10 档位控制的更复杂继电器被研制出来。
In 1898, Nikola Tesla filed a patent for an invention he called “teleautomation”, which he demonstrated with a radio-controlled miniature boat, the first remote control device ever made. The remote control system contained a method for decoding Hertzian waves. This system would toggle actions based on different signals, functioning as an AND gate. 1898 年,尼古拉·特斯拉为其发明的“远程自动化技术”申请了专利,并通过一艘无线电遥控微型船完成了技术演示,这艘船也是人类史上首款遥控设备。该遥控系统搭载了赫兹波解码技术,可根据不同的信号触发不同的动作,其工作原理与与门一致。
The first digital, programmable computing devices’ logic circuitry laid in vacuum tubes. This includes famous computers like ENIAC, Colossus, and Alan Turing’s Pilot Ace. These early digital computers were enormous and had thousands of vacuum tubes. In order to make computing devices accessible to the public, the logic circuitry would need to shrink. 首款数字可编程计算设备的逻辑电路以真空管为核心元件,经典的 ENIAC 计算机、巨人计算机以及艾伦·图灵设计的领航者 ACE 计算机均属此类。这些早期数字计算机体积庞大,内部搭载了数千根真空管。若要让计算设备走向民用,其逻辑电路必须实现微型化。
 ENIAC occupied 1600 square feet of space. A modern smartphone has about 12,000 times as much computing power. Courtesy of the US Army ENIAC 计算机的占地面积达 1600 平方英尺,而一台现代智能手机的运算能力约为其 12000 倍。图片由美国陆军提供
ENIAC occupied 1600 square feet of space. A modern smartphone has about 12,000 times as much computing power. Courtesy of the US Army ENIAC 计算机的占地面积达 1600 平方英尺,而一台现代智能手机的运算能力约为其 12000 倍。图片由美国陆军提供
This needed decrease in size came in the 1960s with resistor-transistor logic (RTL) and transistor-transistor logic (TTL). RTLs were the first logic devices to be incorporated into integrated circuits and were later used in the Apollo guidance computer. The first TTL integrated circuits were developed in 1963 by Sylvania and were popularized by TI’s 7400 series. Since then, modern logic circuitry has been shrinking these concepts and adding additional Boolean gates. 20 世纪 60 年代,电阻-晶体管逻辑电路(RTL)与晶体管-晶体管逻辑电路(TTL)的出现,实现了逻辑电路的微型化需求。电阻-晶体管逻辑电路是首款被集成到集成电路中的逻辑器件,后续还被应用于阿波罗登月计划的制导计算机。1963 年,西屋电气研制出首款晶体管-晶体管逻辑集成电路,德州仪器推出的 7400 系列则让该类型电路实现了普及。自此,现代逻辑电路在这些理论基础上不断向微型化发展,同时新增了多种布尔逻辑门类型。
Digital Logic Today
当代数字逻辑
Centuries of innovation have led to tiny and powerful logic devices like FPGAs, PLCs, and Pico Gates, which allow tiny devices to have computing power and control functionality that dwarfs the massive computers of old. These days, there are tiny logic packages for just about every function imaginable, whether it comes in an array or a discrete package. 历经数百年的技术革新,现场可编程门阵列(FPGA)、可编程逻辑控制器(PLC)以及微型逻辑门(Pico Gates)等微型化、高性能逻辑器件应运而生。这些器件让小型设备拥有了远超早期大型计算机的运算与控制能力。如今,各类功能的微型逻辑器件已实现全覆盖,形式上既包括阵列式,也包括分立式。
A Short History of Logic
逻辑简史
SQC Consulting, Mallow, County Cork, Ireland Gerard O’Regan First Online: 10 August 2017
Key Topics / 关键主题
-
Syllogistic logic / 三段论逻辑
-
Fallacies / 谬误
-
Paradoxes / 悖论
-
Stoic logic / 斯多葛逻辑
-
Boole’s symbolic logic / 布尔符号逻辑
-
Digital computing / 数字计算
-
Propositional logic / 命题逻辑
-
Predicate logic / 谓词逻辑
-
Universal and existential quantifiers / 全称量词与存在量词
1 Introduction
1 引言
Logic is concerned with reasoning and with establishing the validity of arguments. It allows conclusions to be deduced from premises according to logical rules, and the logical argument establishes the truth of the conclusion provided that the premises are true. 逻辑研究推理及论证有效性的建立。它允许根据逻辑规则从前提推导出结论,且若前提为真,逻辑论证可确立结论的真实性。
The origins of logic are with the Greeks who were interested in the nature of truth. The sophists (e.g. Protagoras and Gorgias) were teachers of rhetoric, who taught their pupils techniques in winning an argument and convincing an audience. Plato explores the nature of truth in some of his dialogues, and he is critical of the position of the sophists who argue that there is no absolute truth, and that truth instead is always relative to some frame of reference. The classic sophist position is stated by Protagoras “Man is the measure of all things: of things which are, that they are, and of things which are not, that they are not”. In other words, what is true for you is true for you, and what is true for me is true for me. 逻辑的起源可追溯至对真理本质感兴趣的古希腊人。智者学派(如普罗泰戈拉和高尔吉亚)是修辞学教师,他们向学生传授赢得辩论和说服听众的技巧。柏拉图在其部分对话录中探讨了真理的本质,并对智者学派的观点提出批判——智者学派认为不存在绝对真理,真理始终相对于某一参照框架而言。普罗泰戈拉提出了经典的智者学派主张:“人是万物的尺度:是存在者存在的尺度,也是不存在者不存在的尺度。” 换句话说,对你而言为真的东西对你来说就是真的,对我而言为真的东西对我来说就是真的。
Socrates had a reputation for demolishing an opponent’s position, and the Socratic enquiry consisted of questions and answers in which the opponent would be led to a conclusion incompatible with his original position. The approach was similar to a reductio ad absurdum argument, although Socrates was a moral philosopher who did no theoretical work on logic. 苏格拉底以推翻对手的观点而闻名,苏格拉底问答法通过一连串提问与回答,引导对手得出与其原始立场相矛盾的结论。这种方法类似于归谬法论证,尽管苏格拉底是一位道德哲学家,并未在逻辑领域开展理论研究。
Aristotle did important work on logic, and he developed a system of logic, syllogistic logic, that remained in use up to the nineteenth century. Syllogistic logic is a “term-logic”, with letters used to stand for the individual terms. A syllogism consists of two premises and a conclusion, where the conclusion is a valid deduction from the two premises. Aristotle also did some early work on modal logic and was the founder of the field. 亚里士多德在逻辑领域做出了重要贡献,他发展了一套名为三段论逻辑的体系,该体系一直沿用至 19 世纪。三段论逻辑是一种“词项逻辑”,用字母代表各个词项。一个三段论由两个前提和一个结论组成,其中结论是从两个前提中有效推导得出的。亚里士多德还对模态逻辑进行了早期研究,是该领域的奠基人。
The Stoics developed an early form of propositional logic, where the assertibles (propositions) have a truth-value such that at any time they are either true or false. The assertibles may be simple or non-simple, and various connectives such as conjunctions, disjunctions and implication are used in forming more complex assertibles. 斯多葛学派发展了早期的命题逻辑,其中可断言句(命题)具有真值,即在任何时刻要么为真,要么为假。可断言句可分为简单句和非简单句,人们会使用合取、析取和蕴含等多种联结词来构成更复杂的可断言句。
George Boole developed his symbolic logic in the mid-1800s, and it later formed the foundation for digital computing. Boole argued that logic should be considered as a separate branch of mathematics, rather than a part of philosophy. He argued that there are mathematical laws to express the operation of reasoning in the human mind, and he showed how Aristotle’s syllogistic logic could be reduced to a set of algebraic equations. 乔治·布尔于 19 世纪中叶创立了符号逻辑,该逻辑后来成为数字计算的基础。布尔认为,逻辑应被视为数学的一个独立分支,而非哲学的一部分。他提出,存在数学定律可表达人类思维中的推理过程,并展示了如何将亚里士多德的三段论逻辑简化为一组代数方程。
Logic plays a key role in reasoning and deduction in mathematics, but it is considered a separate discipline to mathematics. There were attempts in the early twentieth century to show that all mathematics can be derived from formal logic, and that the formal system of mathematics would be complete, with all the truths of mathematics provable in the system (see Chap. 13 of [1]). However, this program failed when the Austrian logician, Kurt Gödel, showed that that there are truths in the formal system of arithmetic that cannot be proved within the system (i.e. first-order arithmetic is incomplete). 逻辑在数学的推理和演绎中起着关键作用,但它被视为与数学独立的学科。20 世纪初,有人试图证明所有数学都可从形式逻辑推导而来,且数学的形式系统是完备的——所有数学真理都能在该系统中得到证明(参见文献 [1] 的第 13 章)。然而,奥地利逻辑学家库尔特·哥德尔证明了算术形式系统中存在无法在系统内证明的真理(即一阶算术是不完备的),这一计划随之失败。
2 Syllogistic Logic
2 三段论逻辑
Early work on logic was done by Aristotle in the fourth century B.C. in the Organon [2]. Aristotle regarded logic as a useful tool of enquiry into any subject, and he developed syllogistic logic. This is a form of reasoning in which a conclusion is drawn from two premises, where each premise is in a subject–predicate form. A common or middle term is present in each of the two premises but not in the conclusion. For example: 公元前 4 世纪,亚里士多德在《工具论》[2] 中开展了早期逻辑研究。亚里士多德将逻辑视为探究任何学科的有用工具,并发展了三段论逻辑。这是一种推理形式,结论从两个前提中得出,每个前提均为主谓结构。两个前提中存在一个共同的词项(中项),但该词项不在结论中出现。例如:
All Greeks are mortal,
所有希腊人都是会死的
Socrates is a Greek,
苏格拉底是希腊人
Therefore Socrates is mortal, 因此苏格拉底是会死的
\\begin{array}{l} \\text{All Greeks are mortal, \\qquad\\quad所有希腊人都是会死的} \\\\ \\text{Socrates is a Greek, \\quad\\quad\\qquad苏格拉底是希腊人} \\\\ \\hline \\text{Therefore Socrates is mortal, 因此苏格拉底是会死的} \\end{array}
All Greeks are mortal, 所有希腊人都是会死的Socrates is a Greek, 苏格拉底是希腊人Therefore Socrates is mortal, 因此苏格拉底是会死的
The common (or middle) term in this example is “Greek”. It occurs in both premises but not in the conclusion. The above argument is valid, and Aristotle studied and classified the various types of syllogistic arguments to determine those that were valid or invalid. Each premise contains a subject and a predicate, and the middle term may act as subject or a predicate. Each premise is a positive or negative affirmation, and an affirmation may be universal or particular. The universal and particular affirmations and negatives are described in Table 5.1. 该例子中的共同(中)项是“希腊人”,它在两个前提中都出现,但未在结论中出现。上述论证是有效的,亚里士多德对各种类型的三段论论证进行了研究和分类,以确定其有效性。每个前提都包含一个主项和一个谓项,中项既可以作为主项,也可以作为谓项。每个前提要么是肯定陈述,要么是否定陈述,且陈述要么是全称的,要么是特称的。全称与特称的肯定陈述和否定陈述如表 5.1 所示。
Table 5.1 Types of syllogistic premises 表 5.1 三段论前提的类型
| Universal affirmative 全称肯定 | G A M | All Greeks are mortal 所有希腊人都是会死的 |
| Universal negative 全称否定 | G E M | No Greek is mortal 没有希腊人是会死的 |
| Particular affirmative 特称肯定 | G I M | Some Greek is mortal 有些希腊人是会死的 |
| Particular negative 特称否定 | G O M | Some Greek is not mortal 有些希腊人不是会死的 |
This leads to four basic forms of syllogistic arguments (Table 5.2) where the middle is the subject of both premises; the predicate of both premises; and the subject of one premise and the predicate of the other premise. 这产生了四种基本的三段论论证形式(表 5.2),分别对应:中项是两个前提的主项;中项是两个前提的谓项;中项是一个前提的主项且是另一个前提的谓项。
Table 5.2 Forms of syllogistic premises 表 5.2 三段论前提的形式
| Premise 1 前提 1 | M P | P M | P M | M P |
| Premise 2 前提 2 | M S | S M | M S | S M |
| Conclusion 结论 | S P | S P | S P | S P |
There are four types of premises (A, E, I, O) and therefore sixteen sets of premise pairs for each of the forms above. However, only some of these premise pairs will yield a valid conclusion. Aristotle went through every possible premise pair to determine whether a valid argument may be derived. The syllogistic argument above is of form (iv) and is valid: 前提有四种类型(A、E、I、O),因此每种形式下有 16 组前提对。然而,只有部分前提对能得出有效结论。亚里士多德逐一分析了所有可能的前提对,以确定是否能推导出有效论证。上述三段论论证属于形式(iv),且是有效的:
G A M
S I G
——-
S I M
Syllogistic logic is a “term-logic” with letters used to stand for the individual terms. Syllogistic logic was the first attempt at a science of logic, and it remained in use up to the nineteenth century. There are many limitations to what it may express, and on its suitability as a representation of how the mind works. 三段论逻辑是一种“词项逻辑”,用字母代表各个词项。它是逻辑科学化的首次尝试,一直沿用至 19 世纪。但它在表达能力上存在诸多局限,作为人类思维运作方式的表征也不够贴切。
3 Paradoxes and Fallacies
3 悖论与谬误
A paradox is a statement that apparently contradicts itself, and it presents a situation that appears to defy logic. Some logical paradoxes have a solution, whereas others are contradictions or invalid arguments. There are many examples of paradoxes, and they often arise due to self-reference in which one or more statements refer to each other. We discuss several paradoxes such as the liar paradox and the sorites paradox, which were invented by Eubulides of Miletus, and the barber paradox, which was introduced by Russell to explain the contradictions in naïve set theory. 悖论是一种表面上自相矛盾的陈述,呈现出看似违背逻辑的情境。有些逻辑悖论存在解决方案,而另一些则是矛盾或无效论证。悖论有许多例子,其产生往往源于自指——即一个或多个陈述相互指代。我们将讨论几个悖论,例如米利都的欧布里德提出的说谎者悖论和谷堆悖论,以及罗素为解释朴素集合论中的矛盾而引入的理发师悖论。
An example of the liar paradox is the statement “Everything that I say is false”, which is made by the liar. This looks like a normal sentence, but it is also saying something about itself as a sentence. If the statement is true, then the statement must be false, since the meaning of the sentence is that every statement (including the current statement) made by the liar is false. If the current statement is false, then the statement that everything that I say is false is false, and so this must be a true statement. 说谎者悖论的一个例子是说谎者所说的“我所说的一切都是假的”。这句话看似普通,但它同时也在对自身作为一个句子进行陈述。如果该陈述为真,那么由于句子的含义是说谎者所说的每一句话(包括当前这句话)都是假的,因此该陈述必须为假;如果当前陈述为假,那么“我所说的一切都是假的”这一说法就是假的,因此它又必须是一个真陈述。
The Epimenides paradox is a variant of the liar paradox. Epimenides was a Cretan who allegedly stated “All Cretans are liars”. If the statement is true, then since Epimenides is Cretan, he must be a liar, and so the statement is false and we have a contradiction. However, if we assume that the statement is false and that Epimenides is lying about all Cretan being liars, then we may deduce (without contradiction) that there is at least one Cretan who is truthful. So in this case, the paradox can be avoided. 埃庇米尼得斯悖论是说谎者悖论的一个变体。埃庇米尼得斯是克里特人,据称他曾说过“所有克里特人都是骗子”。如果该陈述为真,那么由于埃庇米尼得斯是克里特人,他必然是骗子,因此该陈述为假,产生矛盾;然而,如果我们假设该陈述为假,即埃庇米尼得斯关于“所有克里特人都是骗子”的说法是谎言,那么我们可以(无矛盾地)推导出至少有一个克里特人是诚实的。因此,在这种情况下,悖论可以被避免。
The sorites paradox (paradox of the heap) involves a heap of sand in which grains are individually removed. It is assumed that removing a single grain of sand does not turn a heap into a non-heap, and the paradox is to consider what happens after when the process is repeated often enough. Is a single remaining grain a heap? When does it change from being a heap to a non-heap? This paradox may be avoided by specifying a fixed boundary of the number of grains of sand required to form a heap, or to define a heap as a collection of multiple grains (≥2 grains). Then, any collection of grains of sand less than this boundary is not a heap. 谷堆悖论(堆悖论)涉及一堆沙子,其中每次只移除一粒沙。假设移除一粒沙不会使一堆沙子变成非堆,那么悖论就在于:当这个过程重复足够多次后会发生什么?仅剩一粒沙时还是堆吗?它何时从堆变成非堆?解决这一悖论的方法可以是设定构成堆所需的沙子粒数的固定界限,或将堆定义为多粒沙子的集合(≥2 粒)。这样一来,任何少于该界限的沙子集合都不是堆。
The barber paradox is a variant of Russell’s paradox (a contradiction in naïve set theory), which was discussed in Chap. 4. In a village, there is a barber who shaves everyone who does not shave himself, and no one else. Who shaves the barber? The answer to this question results in a contradiction, as the barber cannot shave himself, since he shaves only those who do not shave themselves. Further, as the barber does not shave himself then he falls into the group of people who would be shaved by the barber (himself). Therefore, we conclude that there is no such barber. 理发师悖论是罗素悖论(朴素集合论中的一个矛盾)的变体,罗素悖论在第 4 章已讨论过。在一个村庄里,有一位理发师,他给所有不自己刮胡子的人刮胡子,且只给这些人刮胡子。那么谁给理发师刮胡子?这个问题的答案会产生矛盾:因为理发师只给不自己刮胡子的人刮胡子,所以他不能给自己刮胡子;但另一方面,由于理发师不自己刮胡子,他又属于会被理发师(他自己)刮胡子的人群。因此,我们得出结论:不存在这样的理发师。
Table 5.3 Fallacies in arguments 表 5.3 论证中的谬误
| Hasty/Accident generalization 轻率/偶然概括 | This is a bad argument that involves a generalization that disregards exceptions 一种糟糕的论证,其概括过程忽略了例外情况 |
| Slippery slope 滑坡谬误 | This argument outlines a chain reaction leading to a highly undesirable situation that will occur if a certain situation is allowed. The claim is that even if one step is taken onto the slippery slope, then we will fall all the way down to the bottom 该论证描绘了一个连锁反应,声称若允许某一情况发生,将导致极具危害性的结果。其主张是,一旦踏上“滑坡”的第一步,就会一路滑到谷底 |
| Against the person Ad Hominem 人身攻击谬误 | The focus of this argument is to attack the person rather than the argument that the person has made 论证的焦点是攻击提出观点的人,而非其提出的论证本身 |
| Appeal to people Ad Populum 诉诸公众谬误 | This argument involves an appeal to popular belief to support an argument, with a claim that the majority of the population supports this argument. However, popular opinion is not always correct 借助普遍的信念来支持论证,声称大多数人都认同该观点。但公众意见并非总是正确的 |
| Appeal to authority (Ad Verecundiam) 诉诸权威谬误 | This argument is when an appeal is made to an authoritative figure to support an argument, and where the authority is not an expert in this area 试图借助权威人物的声望支持论证,但该权威在相关领域并非专家 |
| Appeal to pity (Ad Misericordiam) 诉诸怜悯谬误 | This is where the arguer tries to get people to accept a conclusion by making them feel sorry for someone 论证者试图通过让人们同情某人来使其接受结论 |
| Appeal to ignorance 诉诸无知谬误 | The arguer makes the case that there is no conclusive evidence on the issue at hand and that therefore his conclusion should be accepted 论证者声称当前议题不存在确凿证据,因此应接受其结论 |
| Straw man argument 稻草人谬误 | The arguer sets up a version of an opponent’s position of his argument and defeats this watered down version of his opponent’s position 论证者先歪曲对手的立场,构建一个弱化版的观点,然后反驳这个虚构的立场 |
| Begging the question 循环论证谬误 | This is a circular argument where the arguer relies on a premise that says the same thing as the conclusion and without providing any real evidence for the conclusion 论证过程是循环的,论证者依赖的前提与结论表述的是同一回事,且未为结论提供任何真实证据 |
| Red herring 转移话题谬误 | The arguer goes off on a tangent that has nothing to do with the argument in question 论证者偏离主题,引入与当前论证无关的内容 |
| False dichotomy 虚假二分法谬误 | The arguer presents the case that there are only two possible outcomes (often there are more). One of the possible outcomes is then eliminated leading to the desired outcome. The argument suggests that there is only one outcome 论证者声称只有两种可能的结果(通常实际存在更多结果),然后排除其中一种结果,从而得出自己想要的结论,暗示该结果是唯一可能的 |
The purpose of a debate is to convince an audience of the correctness of your position and to challenge and undermine your opponent’s position. Often, the arguments made are factual, but occasionally individuals skilled in rhetoric and persuasion will introduce bad arguments as a way to persuade the audience. Aristotle studied and classified bad arguments (known as fallacies), and these include fallacies such as the ad hominem argument; the appeal to authority argument; and the straw man argument. The fallacies are described in more detail in Table 5.3. 辩论的目的是让听众相信你的立场是正确的,并质疑和削弱对手的立场。通常,辩论中提出的论证是基于事实的,但有时擅长修辞和说服技巧的人会使用糟糕的论证(即谬误)来劝说听众。亚里士多德对这些糟糕的论证进行了研究和分类,包括人身攻击谬误、诉诸权威谬误和稻草人谬误等。表 5.3 对这些谬误进行了更详细的描述。
4 Stoic Logic
4 斯多葛逻辑
The Stoic school¹ was founded in the Hellenistic period by Zeno of Citium (in Cyprus) in the late fourth/early third century B.C. (Fig. 5.1). The school presented its philosophy as a way of life, and it emphasized ethics as the main focus of human knowledge. The Stoics stressed the importance of living a good life in harmony with nature. 斯多葛学派¹ 由塞浦路斯的季蒂昂的芝诺在公元前 4 世纪末至公元前 3 世纪初的希腊化时期创立(图 5.1)。该学派将其哲学视为一种生活方式,强调伦理是人类知识的核心。斯多葛学派注重与自然和谐共处的美好生活。
 Zeno of Citium
Zeno of Citium
¹ The origin of the word Stoic is from the Stoa Poikile (Στοά Ποικίλη), which was a covered walkway in the Agora of Athens. Zeno taught his philosophy in a public space at this location, and his followers became known as Stoics. ¹ “Stoic”(斯多葛)一词源于“Stoa Poikile”(彩绘柱廊),这是雅典广场上的一条有顶走廊。芝诺在此公共空间传授其哲学思想,其追随者因此被称为“斯多葛学派”。
The Stoics recognized the importance of reason and logic, and Chrysippus, the head of the Stoics in the third century B.C., developed an early version of propositional logic. This was a system of deduction in which the smallest unanalyzed expressions are assertibles (Stoic equivalent of propositions). The assertibles have a truth-value such that at any moment of time they are either true or false. True assertibles are viewed as facts in the Stoic system of logic, and false assertibles are defined as the contradictories of true ones. 斯多葛学派认识到理性和逻辑的重要性,公元前 3 世纪斯多葛学派的领袖克吕西波发展了早期的命题逻辑。这是一种演绎系统,其中最小的未分析表达式是可断言句(斯多葛学派对命题的称呼)。可断言句具有真值,即在任何时刻要么为真,要么为假。在斯多葛逻辑体系中,真的可断言句被视为事实,假的可断言句则被定义为真可断言句的矛盾命题。
Truth is temporal, and assertions may change their truth-value over time. The assertibles may be simple or non-simple (more than one assertible), and there may be present tense, past tense and future tense assertibles. Chrysippus distinguished between simple and compound propositions, and he introduced a set of logical connectives for conjunction, disjunction and implication that are used to form non-simple assertibles from existing assertibles. 真理具有时间性,断言的真值会随时间变化。可断言句可分为简单句和非简单句(包含多个可断言句),且有现在时、过去时和将来时之分。克吕西波区分了简单命题和复合命题,并引入了一组逻辑联结词(合取、析取和蕴含),用于从现有可断言句构建非简单可断言句。
The conjunction connective is of the form “both … and …”, and it has two conjuncts. The disjunction connective is of the form “either … or … or …”, and it consists of two or more disjuncts. Conditionals are formed from the connective “if …, …”, and they consist of an antecedent and a consequence. 合取联结词的形式为“既……又……”,包含两个合取支;析取联结词的形式为“要么……要么……要么……”,包含两个或多个析取支;条件句由联结词“如果……那么……”构成,包含前件和后件。
His deductive system included various logical argument forms such as modus ponens and modus tollens. His propositional logic differed from syllogistic logic, in that the Stoic logic was based on propositions (or statements) as distinct from Aristotle’s term-logic. However, he could express the universal affirmation in syllogistic logic (e.g. All As are B) by rephrasing it as a conditional statement that if something is A then it is B. 他的演绎系统包含多种逻辑论证形式,如肯定前件式和否定后件式。他的命题逻辑与三段论逻辑不同:斯多葛逻辑以命题(或陈述)为基础,而亚里士多德的逻辑是词项逻辑。不过,他可以将三段论逻辑中的全称肯定命题(如“所有 A 都是 B”)重新表述为条件句“如果某物是 A,那么它是 B”。
Chrysippus’s propositional logic did not replace Aristotle’s syllogistic logic, and syllogistic logic remained in use up to the mid-nineteenth century. George Boole developed his symbolic logic in the mid-1800s, and his logic later formed the foundation for digital computing. Boole’s symbolic logic is discussed in the next section. 克吕西波的命题逻辑并未取代亚里士多德的三段论逻辑,三段论逻辑一直沿用至 19 世纪中叶。乔治·布尔于 19 世纪中叶创立了符号逻辑,该逻辑后来成为数字计算的基础。下一节将讨论布尔的符号逻辑。
5 Boole’s Symbolic Logic
5 布尔符号逻辑
George Boole (Fig. 5.2) was born in Lincoln, England, in 1815. His father (a cobbler who was interested in mathematics and optical instruments) taught him mathematics and showed him how to make optical instruments. Boole inherited his father’s interest in knowledge, and he was self-taught in mathematics and Greek. He taught at various schools near Lincoln, and he developed his mathematical knowledge by working his way through Newton’s Principia, as well as applying himself to the work of mathematicians such as Laplace and Lagrange. 乔治·布尔(图 5.2)于 1815 年出生在英国林肯郡。他的父亲是一名鞋匠,对数学和光学仪器感兴趣,教他数学并向他展示如何制作光学仪器。布尔继承了父亲对知识的热爱,自学了数学和希腊语。他在林肯郡附近的多所学校任教,通过研读牛顿的《自然哲学的数学原理》以及拉普拉斯、拉格朗日等数学家的著作,不断提升自己的数学水平。

George Boole
He published regular papers from his early twenties, and these included contributions to probability theory, differential equations and finite differences. He developed his symbolic algebra, which is the foundation for modern computing, and he is considered (along with Babbage) to be one of the grandfathers of computing. His work was theoretical, and he never actually built a computer or calculating machine. However, Boole’s symbolic logic was the perfect mathematical model for switching theory, and for the design of digital circuits. 他从二十出头就开始定期发表论文,内容涉及概率论、微分方程和有限差分等领域。他创立的符号代数成为现代计算的基础,他也因此与巴贝奇一同被视为“计算之父”之一。他的研究属于理论层面,从未实际制造过计算机或计算器,但布尔符号逻辑为开关理论和数字电路设计提供了完美的数学模型。
Boole became interested in formulating a calculus of reasoning, and he published a pamphlet titled “Mathematical Analysis of Logic” in 1847 [3]. This short book developed novel ideas on a logical method, and he argued that logic should be considered as a separate branch of mathematics, rather than a part of philosophy. He argued that there are mathematical laws to express the operation of reasoning in the human mind, and he showed how Aristotle’s syllogistic logic could be reduced to a set of algebraic equations. He corresponded regularly on logic with Augustus De Morgan.² 布尔对构建推理演算产生了兴趣,并于 1847 年出版了题为《逻辑的数学分析》的小册子 [3]。这本短书提出了关于逻辑方法的新观点,他主张逻辑应被视为数学的一个独立分支,而非哲学的一部分。他认为存在数学定律可表达人类思维中的推理过程,并展示了如何将亚里士多德的三段论逻辑简化为一组代数方程。他还与奥古斯塔斯·德摩根² 就逻辑问题定期通信。
² De Morgan was a nineteenth British mathematician based at University College London. De Morgan’s laws in Set Theory and Logic state that:
(
A
∪
B
)
c
=
A
c
∩
B
c
(A \\cup B)^c = A^c \\cap B^c
(A∪B)c=Ac∩Bc and
¬
(
A
∨
B
)
≡
¬
A
∧
¬
B
\\neg(A \\vee B) \\equiv \\neg A \\land \\neg B
¬(A∨B)≡¬A∧¬B ² 德摩根是 19 世纪英国数学家,任职于伦敦大学学院。集合论和逻辑中的德摩根定律指出:
(
A
∪
B
)
c
=
A
c
∩
B
c
(A \\cup B)^c = A^c \\cap B^c
(A∪B)c=Ac∩Bc 且
¬
(
A
∨
B
)
≡
¬
A
∧
¬
B
\\neg(A \\vee B) \\equiv \\neg A \\land \\neg B
¬(A∨B)≡¬A∧¬B
He introduced two quantities “0” and “1” with the quantity 1 used to represent the universe of thinkable objects (i.e. the universal set), and the quantity 0 represents the absence of any objects (i.e. the empty set). He then employed symbols such as
x
x
x,
y
y
y,
z
z
z, to represent collections or classes of objects given by the meaning attached to adjectives and nouns. Next, he introduced three operators (+, − and ×) that combined classes of objects. 他引入了两个量“0”和“1”:1 代表所有可思考对象的集合(即全集),0 代表没有任何对象的集合(即空集)。随后,他使用
x
x
x、
y
y
y、
z
z
z 等符号代表由形容词和名词含义所界定的对象集合或类。接着,他引入了三种运算符(+、− 和 ×)来组合对象类。
The expression
x
y
xy
xy (i.e.
x
x
x multiplied by
y
y
y or
x
×
y
x \\times y
x×y) combines the two classes
x
x
x,
y
y
y to form the new class
x
y
xy
xy (i.e. the class whose objects satisfy the two meanings represented by the classes
x
x
x and
y
y
y). Similarly, the expression
x
+
y
x + y
x+y combines the two classes
x
x
x,
y
y
y to form the new class
x
+
y
x + y
x+y (that satisfies either the meaning represented by class
x
x
x or class
y
y
y). The expression
x
−
y
x – y
x−y combines the two classes
x
x
x,
y
y
y to form the new class
x
−
y
x – y
x−y. This represents the class that satisfies the meaning represented by class
x
x
x but not class
y
y
y. The expression
(
1
−
x
)
(1 – x)
(1−x) represents objects that do not have the attribute that represents class
x
x
x. 表达式
x
y
xy
xy(即
x
x
x 乘以
y
y
y 或
x
×
y
x \\times y
x×y)将两个类
x
x
x 和
y
y
y 组合成新的类
x
y
xy
xy(即对象同时满足
x
x
x 类和
y
y
y 类所代表含义的类)。类似地,表达式
x
+
y
x + y
x+y 将两个类
x
x
x 和
y
y
y 组合成新的类
x
+
y
x + y
x+y(即对象满足
x
x
x 类或
y
y
y 类所代表含义的类)。表达式
x
−
y
x – y
x−y 将两个类
x
x
x 和
y
y
y 组合成新的类
x
−
y
x – y
x−y,代表满足
x
x
x 类含义但不满足
y
y
y 类含义的对象类。表达式
(
1
−
x
)
(1 – x)
(1−x) 代表不具有
x
x
x 类所对应属性的对象。
Thus, if
x
=
b
l
a
c
k
x = black
x=black and
y
=
s
h
e
e
p
y = sheep
y=sheep, then
x
y
xy
xy represents the class of black sheep. Similarly,
(
1
−
x
)
(1 – x)
(1−x) would represent the class obtained by the operation of selecting all things in the world except black things;
x
(
1
−
y
)
x(1 – y)
x(1−y) represents the class of all things that are black but not sheep; and
(
1
−
x
)
(
1
−
y
)
(1 – x)(1 – y)
(1−x)(1−y) would give us all things that are neither sheep nor black. 例如,若
x
=
黑色
x = 黑色
x=黑色 且
y
=
绵羊
y = 绵羊
y=绵羊,则
x
y
xy
xy 代表“黑色绵羊”类;
(
1
−
x
)
(1 – x)
(1−x) 代表“世界上所有非黑色的事物”类;
x
(
1
−
y
)
x(1 – y)
x(1−y) 代表“黑色但非绵羊的事物”类;
(
1
−
x
)
(
1
−
y
)
(1 – x)(1 – y)
(1−x)(1−y) 代表“既非绵羊也非黑色的事物”类。
He showed that these symbols obeyed a rich collection of algebraic laws and could be added, multiplied, etc., in a manner that is similar to real numbers. These symbols may be used to reduce propositions to equations, and algebraic rules may be employed to solve the equations. The rules include: 他证明了这些符号遵循一系列丰富的代数定律,可像实数一样进行加法、乘法等运算。这些符号可将命题转化为方程,并通过代数规则求解方程。相关规则如下:
| 2 |
x + ( y + z ) = ( x + y ) + z x + (y + z) = (x + y) + z x+(y+z)=(x+y)+z |
Associative 结合律 |
| 3 |
x + y = y + x x + y = y + x x+y=y+x |
Commutative 交换律 |
| 4 |
x + ( 1 − x ) = 1 x + (1 – x) = 1 x+(1−x)=1 |
Complementation 互补律 |
| 5 |
x × 1 = x x \\times 1 = x x×1=x |
Multiplicative identity 乘法单位元 |
| 6 |
x × 0 = 0 x \\times 0 = 0 x×0=0 |
Annihilator Law 零元律 |
| 7 |
x + 1 = 1 x + 1 = 1 x+1=1 |
Annihilator Law 零元律 |
| 8 |
x y = y x xy = yx xy=yx |
Commutative 交换律 |
| 9 |
x ( y z ) = ( x y ) z x(yz) = (xy)z x(yz)=(xy)z |
Associative 结合律 |
| 10 |
x ( y + z ) = x y + x z x(y + z) = xy + xz x(y+z)=xy+xz |
Distributive 分配律 |
| 11 |
x ( y − z ) = x y − x z x(y – z) = xy – xz x(y−z)=xy−xz |
Distributive 分配律 |
| 12 |
x 2 = x x^2 = x x2=x |
Idempotent 幂等律 |
These operations are similar to the modern laws of set theory with the set union operation represented by “+”, and the set intersection operation is represented by multiplication. The universal set is represented by “1” and the empty by “0”. The associative and distributive laws hold. Finally, the set complement operation is given by
(
1
−
x
)
(1 – x)
(1−x). 这些运算与现代集合论定律相似:“+”代表集合的并运算,乘法代表集合的交运算,“1”代表全集,“0”代表空集,结合律和分配律均成立,集合的补运算由
(
1
−
x
)
(1 – x)
(1−x) 表示。
Boole applied the symbols to encode Aristotle’s syllogistic logic, and he showed how the syllogisms could be reduced to equations. This allowed conclusions to be derived from premises by eliminating the middle term in the syllogism. He refined his ideas on logic further in his book “An Investigation of the Laws of Thought” [4]. This book aimed to identify the fundamental laws underlying reasoning in the human mind and to give expression to these laws in the symbolic language of a calculus. 布尔将这些符号应用于编码亚里士多德的三段论逻辑,展示了如何将三段论转化为方程。通过消去三段论中的中项,可从前提推导出结论。他在著作《思维规律研究》[4] 中进一步完善了自己的逻辑思想。该书旨在揭示人类思维推理背后的基本定律,并以演算的符号语言表达这些定律。
He considered the equation
x
2
=
x
x^2 = x
x2=x to be a fundamental law of thought. It allows the principle of contradiction to be expressed (i.e. for an entity to possess an attribute and at the same time not to possess it): 他认为方程
x
2
=
x
x^2 = x
x2=x 是思维的基本定律,可用来表达矛盾律(即一个实体不能同时拥有某一属性和不拥有该属性):
x
2
=
x
⇒
x
−
x
2
=
0
⇒
x
(
1
−
x
)
=
0
\\begin{gathered} x^2 = x \\\\ \\Rightarrow x – x^2 = 0 \\\\ \\Rightarrow x(1 – x) = 0 \\end{gathered}
x2=x⇒x−x2=0⇒x(1−x)=0
For example, if
x
x
x represents the class of horses, then
(
1
−
x
)
(1 – x)
(1−x) represents the class of “not-horses”. The product of two classes represents a class whose members are common to both classes. Hence,
x
(
1
−
x
)
x(1 – x)
x(1−x) represents the class whose members are at once both horses and “not-horses”, and the equation
x
(
1
−
x
)
=
0
x(1 – x) = 0
x(1−x)=0 expresses the fact that there is no such class. That is, it is the empty set. 例如,若
x
x
x 代表“马”类,则
(
1
−
x
)
(1 – x)
(1−x) 代表“非马”类。两个类的乘积代表其成员为两个类共有元素的类。因此,
x
(
1
−
x
)
x(1 – x)
x(1−x) 代表“既是马又是非马”的类,而方程
x
(
1
−
x
)
=
0
x(1 – x) = 0
x(1−x)=0 表明不存在这样的类,即该类为空集。
Boole contributed to other areas in mathematics including differential equations, finite differences³ and to the development of probability theory. Des McHale has written an interesting biography of Boole [5]. Boole’s logic appeared to have no practical use, but this changed with Claude Shannon’s 1937 Master’s Thesis, which showed its applicability to switching theory and to the design of digital circuits. 布尔还对数学的其他领域做出了贡献,包括微分方程、有限差分³ 以及概率论的发展。德斯·麦克黑尔为布尔撰写了一本有趣的传记 [5]。布尔逻辑起初看似没有实际用途,但 1937 年克劳德·香农的硕士论文改变了这一局面,该论文展示了布尔逻辑在开关理论和数字电路设计中的适用性。
³ Finite differences are a numerical method used in solving differential equations. ³ 有限差分是一种用于求解微分方程的数值方法。
5.1 Switching Circuits and Boolean Algebra
5.1 开关电路与布尔代数
Claude Shannon showed in his famous Master’s Thesis that Boole’s symbolic algebra provided the perfect mathematical model for switching theory and for the design of digital circuits. It may be employed to optimize the design of systems of electromechanical relays, and circuits with relays solve Boolean algebra problems. The use of the properties of electrical switches to process logic is the basic concept that underlies all modern electronic digital computers. 克劳德·香农在其著名的硕士论文中指出,布尔符号代数为开关理论和数字电路设计提供了完美的数学模型。它可用于优化机电继电器系统的设计,且继电器电路能够求解布尔代数问题。利用电子开关的特性处理逻辑,是所有现代电子数字计算机的基本原理。
Modern electronic computers use millions (billions) of transistors that act as switches and can change state rapidly. The use of switches to represent binary values is the foundation of modern computing. Digital computers use the binary digits 0 and 1, and a high voltage represents the binary value 1 with a low voltage representing the binary value 0. 现代电子计算机使用数百万(数十亿)个晶体管作为开关,这些晶体管能快速改变状态。利用开关表示二进制值是现代计算的基础。数字计算机使用二进制数字 0 和 1,高电压代表二进制值 1,低电压代表二进制值 0。
A silicon chip may contain billions of tiny electronic switches arranged into logical gates. The basic logic gates are AND, OR and NOT, and these gates may be combined in various ways to perform more complex tasks such as binary arithmetic. Each logic gate has binary value inputs and produces binary value outputs. Boolean logical operations may be implemented by electronic AND, OR and NOT gates, and more complex circuits may be designed from these fundamental building blocks. 一块硅芯片可能包含数十亿个微小的电子开关,这些开关被排列成逻辑门。基本的逻辑门有与门(AND)、或门(OR)和非门(NOT),这些门可通过多种方式组合,执行二进制算术等更复杂的任务。每个逻辑门都有二进制输入和二进制输出。布尔逻辑运算可通过电子与门、或门和非门实现,更复杂的电路可由这些基本组件设计而成。
The example in Fig. 5.3 is that of an “AND” gate which produces the binary value 1 as output only if both inputs are 1. Otherwise, the result will be the binary value 0. Figure 5.4 is an “OR” gate which produces the binary value 1 as output if any of its inputs is 1. Otherwise, it will produce the binary value 0. 图 5.3 所示的是与门(AND),仅当两个输入均为 1 时,输出才为二进制值 1,否则输出为 0。图 5.4 所示的是或门(OR),只要有一个输入为 1,输出就为二进制值 1,否则输出为 0。
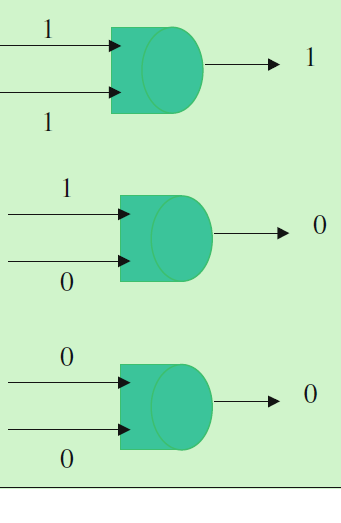 Fig. 5.3 Binary AND operation
Fig. 5.3 Binary AND operation
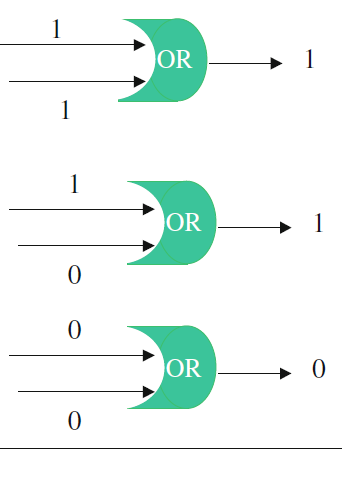 Fig. 5.4 Binary OR operation
Fig. 5.4 Binary OR operation
Finally, a NOT gate (Fig. 5.5) accepts only a single input which it reverses. That is, if the input is “1”, then value “0” is produced and vice versa. 最后,非门(NOT,图 5.5)仅接受一个输入,并将其反转:若输入为“1”,则输出为“0”,反之亦然。 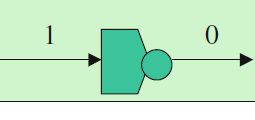 Fig. 5.5 NOT operation
Fig. 5.5 NOT operation
The logic gates may be combined to form more complex circuits. The example in Fig. 5.6 is that of a half-adder of 1 + 0. The inputs to the top OR gate are 1 and 0 which yields the result of 1. The inputs to the bottom AND gate are 1 and 0 which yields the result 0, which is then inverted through the NOT gate to yield binary 1. Finally, the last AND gate receives two 1’s as input, and the binary value 1 is the result of the addition. 逻辑门可组合成更复杂的电路。图 5.6 所示的是 1 + 0 的半加器示例:顶部或门的输入为 1 和 0,输出为 1;底部与门的输入为 1 和 0,输出为 0,该输出经非门反转后得到二进制 1;最后一个与门接收两个 1 作为输入,输出二进制 1,即该加法运算的结果。
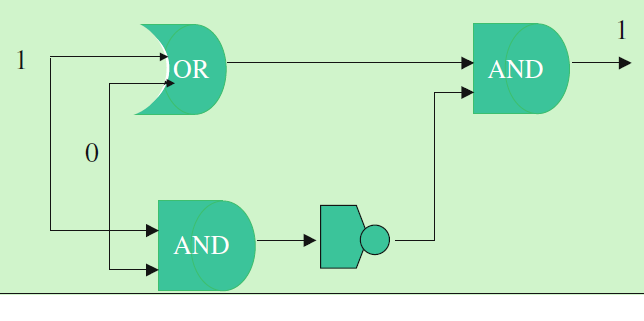
Fig. 5.6 Half-adder
The half-adder computes the addition of two arbitrary binary digits, but it does not calculate the carry. It may be extended to a full-adder that provides a carry for addition. 半加器可计算两个任意二进制数字的和,但不计算进位。它可扩展为能处理进位的全加器。
6 Application of Symbolic Logic to Digital Computing
6 符号逻辑在数字计算中的应用
Claude Shannon (Fig. 5.7) was an American mathematician and engineer who made fundamental contributions to computing. He was the first person⁴ to see the applicability of Boolean algebra to simplify the design of circuits and telephone routing switches. He showed that Boole’s symbolic logic developed in the nineteenth century provided the perfect mathematical model for switching theory and for the subsequent design of digital circuits and computers. 克劳德·香农(图 5.7)是美国数学家和工程师,为计算领域做出了基础性贡献。他是首位⁴ 发现布尔代数可用于简化电路和电话路由开关设计的人。他指出,19 世纪发展起来的布尔符号逻辑为开关理论以及后续的数字电路和计算机设计提供了完美的数学模型。

Fig. 5.7 Claude Shannon
⁴ Victor Shestakov at Moscow State University also proposed a theory of electric switches based on Boolean algebra around the same time as Shannon. However, his results were published in Russian in 1941, whereas Shannon’s were published in 1937. ⁴ 莫斯科国立大学的维克多·舍斯塔科夫几乎与香农同时提出了基于布尔代数的电子开关理论,但他的研究结果于 1941 年以俄语发表,而香农的成果于 1937 年发表。
Vannevar Bush [6] was Shannon’s supervisor at MIT, and Shannon’s initial work was to improve Bush’s mechanical computing device known as the Differential Analyser. This machine had a complicated control circuit that was composed of one hundred switches that could be automatically opened and closed by an electromagnet. Shannon’s insight was his realization that an electronic circuit is similar to Boole’s symbolic algebra, and he showed how Boolean algebra could be employed to optimize the design of systems of electromechanical relays used in the analog computer. He also realized that circuits with relays could solve Boolean algebra problems. 万尼瓦尔·布什 [6] 是香农在麻省理工学院的导师,香农最初的工作是改进布什的机械计算设备——微分分析器。该设备有一个复杂的控制电路,由 100 个可通过电磁铁自动开合的开关组成。香农的关键洞见是认识到电子电路与布尔符号代数的相似性,并展示了如何利用布尔代数优化模拟计算机中机电继电器系统的设计。他还意识到,继电器电路能够求解布尔代数问题。
Shannon’s influential Master’s Thesis is a key milestone in computing, and it shows how to lay out circuits according to Boolean principles. It provides the theoretical foundation of switching circuits, and his insight of using the properties of electrical switches to do Boolean logic is the basic concept that underlies all electronic digital computers. 香农具有深远影响的硕士论文是计算领域的关键里程碑,它展示了如何根据布尔原理设计电路,为开关电路提供了理论基础。他利用电子开关的特性实现布尔逻辑的思想,是所有电子数字计算机的核心原理。
Shannon realized that you could combine switches in circuits in such a manner as to carry out symbolic logic operations. This allowed binary arithmetic and more complex mathematical operations to be performed by relay circuits. He designed a circuit, which could add binary numbers, and he later designed circuits that could make comparisons and thus is capable of performing a conditional statement. This was the birth of digital logic and the digital computing age. 香农认识到,可通过特定方式将电路中的开关组合起来执行符号逻辑运算,这使得继电器电路能够进行二进制算术和更复杂的数学运算。他设计了能进行二进制加法的电路,后来又设计出能进行比较运算的电路,从而实现了条件语句的执行。这标志着数字逻辑和数字计算时代的诞生。
He showed in his Master’s thesis “A Symbolic Analysis of Relay and Switching Circuits” [7] that the binary digits (i.e. 0 and 1) can be represented by electrical switches. The implications of true and false being denoted by the binary digits one and zero were enormous, since it allowed binary arithmetic and more complex mathematical operations to be performed by relay circuits. This provided electronics engineers with the mathematical tool they needed to design digital electronic circuits and provided the foundation of digital electronic design. 他在硕士论文《继电器与开关电路的符号分析》[7] 中指出,二进制数字(即 0 和 1)可通过电子开关表示。用二进制数字 1 和 0 分别表示真和假,这一想法具有重大意义——它使得继电器电路能够进行二进制算术和更复杂的数学运算。这为电子工程师提供了设计数字电子电路所需的数学工具,奠定了数字电子设计的基础。
The design of circuits and telephone routing switches could be simplified with Boole’s symbolic algebra. Shannon showed how to lay out circuitry according to Boolean principles, and his Master’s thesis became the foundation for the practical design of digital circuits. These circuits are fundamental to the operation of modern computers and telecommunication systems, and his insight of using the properties of electrical switches to do Boolean logic is the basic concept that underlies all electronic digital computers. 布尔符号代数可简化电路和电话路由开关的设计。香农展示了如何根据布尔原理布置电路,他的硕士论文成为数字电路实际设计的基础。这些电路是现代计算机和电信系统运行的核心,而他利用电子开关特性实现布尔逻辑的思想,是所有电子数字计算机的基本原理。
7 Frege
7 弗雷格
Gottlob Frege (Fig. 5.8) was a German mathematician and logician who is considered (along with Boole) to be one of the founders of modern logic. He also made important contributions to the foundations of mathematics, and he attempted to show that all of the basic truths of mathematics (or at least of arithmetic) could be derived from a limited set of logical axioms (this approach is known as logicism). 戈特洛布·弗雷格(图 5.8)是德国数学家和逻辑学家,与布尔一同被视为现代逻辑的奠基人之一。他还为数学基础研究做出了重要贡献,试图证明所有数学基本真理(至少是算术真理)都可从一组有限的逻辑公理推导而来(这种方法被称为逻辑主义)。

Fig. 5.8 Gottlob Frege
He invented predicate logic and the universal and existential quantifiers, and predicate logic was a significant advance on Aristotle’s syllogistic logic. Predicate logic is described in more detail in Chap. 6. 他创立了谓词逻辑以及全称量词和存在量词,谓词逻辑是对亚里士多德三段论逻辑的重大突破。第 6 章将更详细地介绍谓词逻辑。
Frege’s first logical system, the 1879 Begriffsschrift, contained nine axioms and one rule of inference. It was the axiomatization of logic, and it was complete in its treatment of propositional logic and first-order predicate logic. He published several important books on logic, including Begriffsschrift, in 1879; Die Grundlagen der Arithmetik (The Foundations of Arithmetic) in 1884; and the two-volume work Grundgesetze der Arithmetik (Basic Laws of Arithmetic), which were published in 1893 and 1903. These books described his invention of axiomatic predicate logic; the use of quantified variables; and the application of his logic to the foundations of arithmetic. 弗雷格的第一个逻辑系统是 1879 年的《概念文字》,该系统包含 9 条公理和 1 条推理规则,是逻辑的公理化体系,对命题逻辑和一阶谓词逻辑的处理是完备的。他出版了多部重要的逻辑著作,包括 1879 年的《概念文字》、1884 年的《算术基础》以及 1893 年和 1903 年出版的两卷本《算术的基本定律》。这些著作阐述了他创立的公理谓词逻辑、量化变量的使用,以及将其逻辑应用于算术基础的研究。
Frege presented his predicate logic in his books, and he began to use it to define the natural numbers and their properties. He had intended producing three volumes of the Basic Laws of Arithmetic, with the later volumes dealing with the real numbers and their properties. However, Bertrand Russell discovered a contradiction in Frege’s system (see Russell’s paradox in Chap. 4), which he communicated to Frege shortly before the publication of the second volume. Frege was astounded by the contradiction and he struggled to find a satisfactory solution, and Russell later introduced the theory of types in the Principia Mathematica as a solution. 弗雷格在其著作中阐述了谓词逻辑,并开始用它定义自然数及其性质。他原本计划撰写三卷本《算术的基本定律》,后续卷册将探讨实数及其性质。然而,伯特兰·罗素在第二卷出版前夕发现了弗雷格系统中的一个矛盾(见第 4 章的罗素悖论),并告知了弗雷格。弗雷格对此感到震惊,努力寻求令人满意的解决方案,而罗素后来在《数学原理》中提出了类型论作为解决方案。
8 Review Questions
8 复习题参考答案
1. What is logic? 什么是逻辑?
Logic is a formal discipline that studies the principles of valid reasoning, argument structure, and the distinction between correct and incorrect inference. It explores the rules governing the connection between premises and conclusions, aiming to establish criteria for evaluating whether an argument can reliably lead from given assumptions to a coherent conclusion. Logic encompasses both formal systems (e.g., syllogistic logic, propositional logic) and informal analysis of reasoning in natural language. Its scope includes the study of logical operators, quantifiers, validity, soundness, and the structure of arguments across mathematical, philosophical, and practical contexts.
逻辑是一门研究有效推理原则、论证结构以及正确与错误推论区分的形式学科。它探究支配前提与结论之间关联的规则,旨在建立评估论证是否能从给定假设可靠推导出连贯结论的标准。逻辑既包含形式系统(如三段论逻辑、命题逻辑),也涉及自然语言推理的非形式分析,其研究范围涵盖逻辑运算符、量词、有效性、可靠性以及数学、哲学和实践场景中的论证结构。
2. What is a fallacy? 什么是谬误?
A fallacy refers to a flaw in the structure or content of an argument that renders it logically invalid or misleading, despite appearing persuasive on the surface. Fallacies can be divided into two broad categories: formal fallacies and informal fallacies. Formal fallacies arise from violations of the rules of formal logic (e.g., incorrect syllogistic structure), while informal fallacies stem from improper use of language, irrelevant premises, or flawed reasoning in content (e.g., attacking the arguer instead of the argument). Fallacies fail to provide sufficient or relevant evidence to support their conclusions, leading to unreliable or false inferences.
谬误指论证在结构或内容上存在的缺陷,使其在逻辑上无效或具有误导性,尽管表面上可能具有说服力。谬误可分为形式谬误和非形式谬误两大类:形式谬误源于对形式逻辑规则的违反(如三段论结构错误),非形式谬误则源于语言使用不当、前提无关或内容层面的推理缺陷(如攻击论证者而非论证本身)。谬误无法提供充分或相关的证据支持结论,导致推论不可靠或虚假。
3. Give examples of fallacies in arguments in natural language (e.g., in politics, marketing, debates) 举例说明自然语言论证中的谬误(如政治、营销、辩论中的例子)
| Appeal to Authority (Ad Verecundiam)诉诸权威谬误 | Politics政治 | “We should adopt this economic policy because a famous actor endorsed it.”“我们应该采纳这项经济政策,因为一位著名演员支持它。” |
| False Dichotomy虚假两难谬误 | Marketing营销 | “Either buy our anti-aging cream now, or your skin will wrinkle permanently in a month.”“要么现在购买我们的抗衰老面霜,要么你的皮肤将在一个月内永久起皱。” |
| Ad Hominem人身攻击谬误 | Debate辩论 | “Your argument about climate change is wrong because you don’t have a PhD in environmental science.”“你关于气候变化的论证是错误的,因为你没有环境科学博士学位。” |
| Slippery Slope滑坡谬误 | Politics政治 | “If we allow same-sex marriage, traditional family values will collapse, and society will descend into chaos.”“如果我们允许同性婚姻,传统家庭价值观将崩溃,社会将陷入混乱。” |
| Appeal to Popularity (Ad Populum)诉诸大众谬误 | Marketing营销 | “Over 90% of people choose our smartphone, so it must be the best on the market.”“超过 90%的人选择我们的智能手机,因此它一定是市场上最好的。” |
| Hasty Generalization草率概括谬误 | Daily Debate日常辩论 | “I met two rude tourists from Country X, so all people from Country X are rude.”“我遇到过两个来自 X 国的粗鲁游客,因此所有 X 国人都很粗鲁。” |
4. Investigate some of the early paradoxes (e.g., the Tortoise and Achilles paradox or the arrow in flight paradox) and give your interpretation of the paradox. 研究一些早期悖论(如龟兔赛跑悖论或飞矢不动悖论),并给出你的解读。
(1)The Tortoise and Achilles Paradox 龟兔赛跑悖论(芝诺悖论之一)
-
Paradox Description: Achilles, the fastest runner, races against a tortoise. The tortoise is given a head start. When Achilles reaches the tortoise’s starting point, the tortoise has moved forward a small distance. When Achilles reaches that new position, the tortoise has moved again, and so on. Logically, Achilles can never catch up to the tortoise, as there are infinitely many small distances to cover.
-
Interpretation: The paradox arises from a misunderstanding of infinite series and continuity. Mathematically, the sum of an infinite series of decreasing positive terms can be finite. For example, if the tortoise has a 10-meter head start, and Achilles runs 10 times faster, the time taken for Achilles to catch up is the sum of 1 second (to cover 10 meters) + 0.1 seconds (to cover the next 1 meter) + 0.01 seconds + … = 1.111… seconds (a finite value). The paradox confuses “infinitely many steps” with “infinite time.” In reality, infinite steps can be completed in finite time, as each step becomes progressively shorter. Philosophically, the paradox challenges the intuition of motion and continuity, highlighting the need for mathematical rigor to resolve apparent contradictions.
-
悖论描述:跑得最快的阿喀琉斯与一只乌龟赛跑,乌龟被赋予先跑的优势。当阿喀琉斯到达乌龟的起跑点时,乌龟已经向前移动了一小段距离;当阿喀琉斯到达乌龟的新位置时,乌龟又再次移动,如此循环往复。从逻辑上看,阿喀琉斯永远无法追上乌龟,因为存在无数个需要覆盖的小段距离。
-
解读:该悖论源于对无穷级数与连续性的误解。从数学角度,无穷多个递减正数项的和可以是有限值。例如,若乌龟拥有 10 米的先跑距离,且阿喀琉斯的速度是乌龟的 10 倍,那么阿喀琉斯追上乌龟所需的时间为 1 秒(覆盖 10 米)+0.1 秒(覆盖下一段 1 米)+0.01 秒+……=1.111……秒(一个有限值)。悖论将“无穷多个步骤”与“无限时间”混淆,实际上无穷多个步骤可在有限时间内完成,因为每个步骤的时长逐渐缩短。从哲学角度,该悖论挑战了人们对运动与连续性的直觉认知,凸显了通过数学严谨性解决表面矛盾的必要性。
(2)The Arrow in Flight Paradox 飞矢不动悖论(芝诺悖论之一)
-
Paradox Description: At any single moment in time, a flying arrow is at a specific position in space. It cannot be in motion at that exact instant, as motion requires a change in position over time. If the arrow is stationary at every moment, then it is never in motion.
-
Interpretation: The paradox relies on a static view of time as a collection of discrete instants. Modern physics and mathematics reject this notion, viewing time as a continuous dimension. Motion is defined as the rate of change of position over time (velocity), which cannot be determined by a single instant but requires observing the arrow’s position across an interval of time. At any instant, the arrow has a velocity (a property that predicts future position changes), even if its position is fixed at that moment. The paradox confuses “being at a position” with “being stationary.” Philosophically, it raises questions about the nature of time, motion, and continuity, emphasizing that concepts like motion depend on relational properties across time, not just isolated moments.
-
悖论描述:在时间的任何一个瞬间,飞行中的箭都处于空间中的某个特定位置。在那个精确的瞬间,箭不可能处于运动状态,因为运动需要位置随时间发生变化。如果箭在每个瞬间都静止不动,那么它永远不会处于运动状态。
-
解读:该悖论依赖于将时间视为离散瞬间集合的静态观点。现代物理学与数学摒弃了这一观念,将时间视为连续维度。运动被定义为位置随时间的变化率(速度),这一概念无法通过单个瞬间确定,而需要观察箭在一段时间间隔内的位置变化。在任何瞬间,箭都具有速度(一种可预测未来位置变化的属性),即便其在该瞬间的位置是固定的。悖论将“处于某个位置”与“静止不动”混淆。从哲学角度,它引发了关于时间、运动与连续性本质的思考,强调运动等概念依赖于跨时间的关系属性,而非孤立的瞬间。
5. What is syllogistic logic and explain its relevance. 什么是三段论逻辑?说明其意义。
- Definition: Syllogistic logic, developed by Aristotle, is a formal system of reasoning that analyzes arguments consisting of three categorical propositions: two premises and one conclusion. Each proposition contains two terms (subject and predicate) and a quantifier (universal or particular) and a copula (affirmative or negative). The three terms are the major term (predicate of the conclusion), minor term (subject of the conclusion), and middle term (connects the two premises). For example:
- Premise 1: All humans are mortal (major premise, contains major term “mortal”).
- Premise 2: All Greeks are humans (minor premise, contains minor term “Greeks”).
- Conclusion: All Greeks are mortal (connects minor and major terms via middle term “humans”).
- Relevance:
- 定义:三段论逻辑由亚里士多德提出,是一种分析由三个直言命题(两个前提和一个结论)构成的论证的形式推理系统。每个命题包含两个项(主项和谓项)、一个量词(全称或特称)和一个联项(肯定或否定)。三个项分别为大项(结论的谓项)、小项(结论的主项)和中项(连接两个前提的项)。例如:
- 前提 1:所有人都是会死的(大前提,包含大项“会死的”)。
- 前提 2:所有希腊人都是人(小前提,包含小项“希腊人”)。
- 结论:所有希腊人都是会死的(通过中项“人”连接小项和大项)。
- 意义:
6. What is stoic logic and explain its relevance. 什么是斯多葛逻辑?说明其意义。
- Definition: Stoic logic, developed by the Stoic school (e.g., Chrysippus) in ancient Greece, is a formal system centered on propositional logic. Unlike Aristotle’s syllogistic logic (which focuses on categorical terms), Stoic logic analyzes arguments composed of propositions (statements that are true or false) and logical connectives (e.g., “and,” “or,” “if…then”). Key components include:
- Simple propositions (e.g., “It is day”) and complex propositions (e.g., “If it is day, then it is light”).
- Logical connectives with well-defined truth conditions (e.g., a conditional proposition is false only when the antecedent is true and the consequent is false).
- Valid argument forms (syllogisms), such as modus ponens (“If P, then Q; P; therefore Q”) and modus tollens (“If P, then Q; not Q; therefore not P”).
- Relevance:
- 定义:斯多葛逻辑由古希腊斯多葛学派(如克吕西波)提出,是一种以命题逻辑为核心的形式系统。与亚里士多德基于词项的三段论逻辑不同,斯多葛逻辑分析由命题(具有真假值的陈述)和逻辑连接词(如“并且”“或者”“如果……那么……”)构成的论证。其核心组成包括:
- 简单命题(如“现在是白天”)和复合命题(如“如果现在是白天,那么天是亮的”)。
- 具有明确真值条件的逻辑连接词(如条件命题仅在前件为真且后件为假时为假)。
- 有效论证形式(三段论),如肯定前件式(“如果 P,那么 Q;P;因此 Q”)和否定后件式(“如果 P,那么 Q;非 Q;因此非 P”)。
- 意义:
7. Explain the significance of the equation
x
2
=
x
x^2 = x
x2=x in Boole’s symbolic logic. 解释布尔符号逻辑中方程
x
2
=
x
x^2 = x
x2=x 的意义。
In George Boole’s symbolic logic (developed in the mid-19th century), the equation
x
2
=
x
x^2 = x
x2=x is a foundational principle with both mathematical and logical implications, rooted in Boole’s goal of formalizing logical reasoning using algebraic methods.
- Logical Interpretation: Boole’s system maps logical concepts to algebraic symbols. Here,
x
x
x represents a class (e.g., “humans”) or a proposition (e.g., “It is raining”). The operation of multiplication (×
\\times
×) corresponds to logical conjunction (“and”). The equationx
2
=
x
x^2 = x
x2=x translates to: “The class of things that arex
x
x andx
x
x is identical to the class of things that arex
x
x” (for class logic), or “The proposition that isx
x
x andx
x
x is equivalent to the propositionx
x
x” (for propositional logic). This reflects the intuitive principle that asserting a statement twice (e.g., “It is raining and it is raining”) adds no new information—it is logically equivalent to asserting it once. - Mathematical Implications: Algebraically,
x
2
=
x
x^2 = x
x2=x simplifies tox
2
−
x
=
0
x^2 – x = 0
x2−x=0 orx
(
1
−
x
)
=
0
x(1 – x) = 0
x(1−x)=0. In Boole’s system,1
1
1 represents the universal class (all things) or the true proposition, and0
0
0 represents the empty class (no things) or the false proposition. The equationx
(
1
−
x
)
=
0
x(1 – x) = 0
x(1−x)=0 thus expresses the law of non-contradiction: “Nothing can be bothx
x
x and notx
x
x” (for classes) or “A proposition cannot be both true and false” (for propositions). This law is a cornerstone of classical logic. - Foundational Role: The equation
x
2
=
x
x^2 = x
x2=x defines the algebraic structure of Boole’s logic, distinguishing it from ordinary arithmetic (wherex
2
=
x
x^2 = x
x2=x holds only forx
=
0
x = 0
x=0 orx
=
1
x = 1
x=1). This structure, later known as a Boolean algebra, imposes constraints that align with logical reasoning. For example, it ensures that logical conjunction is idempotent (applying it multiple times does not change the result), a property essential for valid inference. Boolean algebra later became the mathematical foundation for digital computing, as it models the behavior of binary systems (0s and 1s) used in circuits.
在乔治·布尔于 19 世纪中叶提出的符号逻辑中,方程
x
2
=
x
x^2 = x
x2=x 是一项具有数学与逻辑双重含义的基础性原则,其根源在于布尔试图通过代数方法形式化逻辑推理的目标。
- 逻辑解读:布尔的系统将逻辑概念映射为代数符号。其中,
x
x
x 代表一个类(如“人类”)或一个命题(如“正在下雨”),乘法运算(×
\\times
×)对应逻辑合取(“并且”)。方程x
2
=
x
x^2 = x
x2=x 可译为:“是x
x
x 且是x
x
x 的事物类与是x
x
x 的事物类完全相同”(适用于类逻辑),或“命题x
x
x 且命题x
x
x 与命题x
x
x 等价”(适用于命题逻辑)。这反映了一个直观原则:重复断言同一陈述(如“正在下雨并且正在下雨”)不会增加新信息——其在逻辑上与仅断言一次完全等价。 - 数学含义:从代数角度,
x
2
=
x
x^2 = x
x2=x 可化简为x
2
−
x
=
0
x^2 – x = 0
x2−x=0 或x
(
1
−
x
)
=
0
x(1 – x) = 0
x(1−x)=0。在布尔的系统中,1
1
1 代表全类(所有事物)或真命题,0
0
0 代表空类(无事物)或假命题。因此,方程x
(
1
−
x
)
=
0
x(1 – x) = 0
x(1−x)=0 表达了矛盾律:“没有事物既能是x
x
x 又能是非x
x
x”(适用于类逻辑)或“一个命题不能既为真又为假”(适用于命题逻辑)。该定律是经典逻辑的核心支柱。 - 基础作用:方程
x
2
=
x
x^2 = x
x2=x 定义了布尔逻辑的代数结构,使其区别于普通算术(在普通算术中,x
2
=
x
x^2 = x
x2=x 仅当x
=
0
x = 0
x=0 或x
=
1
x = 1
x=1 时成立)。这种后来被称为布尔代数的结构,施加了与逻辑推理相契合的约束条件。例如,它确保逻辑合取具有幂等性(多次应用不会改变结果),这一属性对有效推理至关重要。布尔代数随后成为数字计算的数学基础,因为它能够建模电路中使用的二进制系统(0 和 1)的行为。
8. Describe how Boole’s symbolic logic provided the foundation for digital computing. 阐述布尔符号逻辑如何为数字计算奠定基础。
George Boole’s symbolic logic, particularly his development of Boolean algebra, laid the mathematical groundwork for digital computing by establishing a formal system that maps logical reasoning to algebraic operations—operations that could later be implemented in hardware. The key connections are as follows:
- Binary Representation: Boolean algebra operates on two values (0 and 1), which correspond to the logical states of “false” and “true.” This binary nature aligns with the physical design of digital computers, where electronic circuits use two voltage levels (e.g., low and high) to represent 0 and 1. Boole’s system provided a mathematical framework for manipulating these binary values.
- Logical Gates: Boolean algebra defines three fundamental operations: conjunction (
×
\\times
×, “and”), disjunction (+
+
+, “or”), and negation (1
−
x
1 – x
1−x, “not”). These operations directly translate to the design of digital logic gates—electronic components that process binary signals. For example: - An AND gate outputs 1 (true) only if both inputs are 1.
- An OR gate outputs 1 if at least one input is 1.
- A NOT gate inverts the input (1 becomes 0, 0 becomes 1). All complex digital circuits (e.g., arithmetic units, memory, processors) are constructed from these basic logic gates, which are direct implementations of Boolean operations.
- Circuit Design and Optimization: Boolean algebra allows engineers to model and simplify digital circuits. By representing a circuit’s desired behavior as a Boolean expression, engineers can use algebraic rules (e.g., distributive law, idempotent law) to minimize the number of gates or inputs, reducing circuit complexity, power consumption, and cost. For example, the expression
x
+
x
y
x + xy
x+xy can be simplified tox
x
x using Boolean algebra, eliminating unnecessary gates. - Formal Verification: Boolean logic provides a rigorous method for verifying the correctness of digital systems. By formalizing the desired behavior of a circuit as a Boolean function, engineers can prove that the circuit’s actual behavior matches the specification, ensuring reliability in critical applications (e.g., aerospace, medical devices).
- Turing Machines and Computability: Boole’s work influenced later developments in computability theory. Alan Turing’s Turing machine, a theoretical model of computation, uses logical operations (rooted in Boolean algebra) to process symbols on a tape. This model established the foundation for modern computing, showing that any computable function can be implemented using logical operations—operations that Boole first formalized.
乔治·布尔的符号逻辑,尤其是他创立的布尔代数,通过建立一套将逻辑推理映射为代数运算的形式系统,为数字计算奠定了数学基础——这些运算后来可通过硬件实现。核心关联如下:
- 二进制表示:布尔代数仅作用于两个值(0 和 1),分别对应逻辑状态“假”和“真”。这种二进制特性与数字计算机的物理设计相契合:电子电路通过两种电压水平(如低电压和高电压)表示 0 和 1。布尔的系统为操控这些二进制值提供了数学框架。
- 逻辑门:布尔代数定义了三种基本运算:合取(
×
\\times
×,“并且”)、析取(+
+
+,“或者”)和否定(1
−
x
1 – x
1−x,“非”)。这些运算直接转化为数字逻辑门的设计——逻辑门是处理二进制信号的电子元件。例如: - 与门(AND gate)仅当两个输入均为 1 时,输出 1(真)。
- 或门(OR gate)若至少一个输入为 1,则输出 1。
- 非门(NOT gate)将输入反转(1 变为 0,0 变为 1)。 所有复杂的数字电路(如算术单元、存储器、处理器)均由这些基本逻辑门构成,而逻辑门正是布尔运算的直接硬件实现。
- 电路设计与优化:布尔代数允许工程师对数字电路进行建模与简化。通过将电路的预期行为表示为布尔表达式,工程师可利用代数规则(如分配律、幂等律)减少门的数量或输入端口,从而降低电路复杂度、功耗与成本。例如,表达式
x
+
x
y
x + xy
x+xy 可通过布尔代数简化为x
x
x,消除不必要的逻辑门。 - 形式验证:布尔逻辑为验证数字系统的正确性提供了严谨方法。通过将电路的预期行为形式化为布尔函数,工程师可证明电路的实际行为与规格说明一致,确保关键应用(如航空航天、医疗设备)中的可靠性。
- 图灵机与可计算性:布尔的研究影响了后续可计算性理论的发展。艾伦·图灵提出的图灵机(一种计算的理论模型),利用植根于布尔代数的逻辑运算处理纸带上的符号。该模型为现代计算奠定了基础,证明任何可计算函数都可通过逻辑运算实现——而这些运算正是布尔首次形式化的内容。
9. Describe Frege’s contributions to logic. 阐述弗雷格对逻辑的贡献。
Gottlob Frege (1848–1925), a German mathematician and philosopher, is widely regarded as the founder of modern mathematical logic. His contributions transformed logic from a tool for analyzing natural language arguments into a rigorous, formal discipline capable of foundational work in mathematics and philosophy. Key contributions include:
- Development of Predicate Logic: Frege introduced predicate logic (also known as first-order logic) in his 1879 work Begriffsschrift (“Concept Script”). Unlike Aristotle’s syllogistic logic (limited to categorical propositions) and Boole’s propositional logic (limited to whole propositions), predicate logic analyzes the internal structure of propositions, distinguishing between predicates (properties or relations) and individuals (objects). For example, the proposition “Socrates is mortal” is analyzed as
P
(
a
)
P(a)
P(a), whereP
P
P is the predicate “is mortal” anda
a
a is the individual “Socrates.” This allows for the formalization of complex statements involving quantifiers (e.g., “All humans are mortal” as∀
x
(
H
(
x
)
→
M
(
x
)
)
\\forall x (H(x) \\rightarrow M(x))
∀x(H(x)→M(x))). - Formalization of Quantifiers: Frege invented the universal quantifier (
∀
\\forall
∀, “for all”) and existential quantifier (∃
\\exists
∃, “there exists”), providing a rigorous way to express generalizations and existence claims. This resolved limitations of earlier logical systems, which could not adequately formalize statements like “Some dogs are brown” or “All primes greater than 2 are odd.” Quantifiers became a core component of modern logic and mathematics. - Distinction Between Sense and Reference: In Über Sinn und Bedeutung (“On Sense and Reference,” 1892), Frege distinguished between the “sense” (Sinn) of a linguistic expression (its cognitive meaning or mode of presentation) and its “reference” (Bedeutung) (the object or truth value it denotes). For example, “the morning star” and “the evening star” have different senses but the same reference (the planet Venus). This distinction clarified issues in logic and language, such as how identity statements (e.g., “Hesperus is Phosphorus”) can be informative.
- Logicism: Frege’s primary goal was to reduce mathematics to logic (a program called logicism). In The Foundations of Arithmetic (1884) and Grundgesetze der Arithmetik (“Basic Laws of Arithmetic,” 1893–1903), he attempted to derive arithmetic (e.g., the definition of natural numbers) from logical axioms and definitions. While Bertrand Russell’s paradox (1901) showed a flaw in Frege’s system (his fifth axiom led to a contradiction), the logicist program influenced later work by Russell, Alfred North Whitehead, and others, and laid the groundwork for mathematical logic as a foundational discipline.
- Formal Language and Axiomatic System: Frege designed a formal language (Begriffsschrift) with precise syntax and semantics, intended to avoid the ambiguities of natural language. He also developed an axiomatic system for logic, with explicit axioms and inference rules, setting a standard for rigor in formal systems. This approach influenced the development of subsequent formal languages in logic, mathematics, and computer science (e.g., programming languages, formal specification languages).
戈特洛布·弗雷格(1848–1925)是德国数学家与哲学家,被广泛视为现代数理逻辑的奠基人。他的贡献将逻辑从一种分析自然语言论证的工具,转变为一门能够为数学与哲学提供基础支持的严谨形式学科。核心贡献包括:
- 谓词逻辑的创立:弗雷格在 1879 年的著作《概念文字》(Begriffsschrift)中引入了谓词逻辑(又称一阶逻辑)。与亚里士多德局限于直言命题的三段论逻辑、布尔局限于完整命题的命题逻辑不同,谓词逻辑分析命题的内部结构,区分谓词(属性或关系)与个体(对象)。例如,命题“苏格拉底是会死的”被分析为
P
(
a
)
P(a)
P(a),其中P
P
P 是谓词“是会死的”,a
a
a 是个体“苏格拉底”。这使得包含量词的复杂陈述能够被形式化(如“所有人都是会死的”形式化为∀
x
(
H
(
x
)
→
M
(
x
)
)
\\forall x (H(x) \\rightarrow M(x))
∀x(H(x)→M(x)))。 - 量词的形式化:弗雷格发明了全称量词(
∀
\\forall
∀,“对所有”)与存在量词(∃
\\exists
∃,“存在”),为表达概括性陈述与存在性陈述提供了严谨方法。这一创新解决了早期逻辑系统的局限性——此前的系统无法充分形式化诸如“有些狗是棕色的”或“所有大于 2 的质数都是奇数”这类陈述。量词随后成为现代逻辑与数学的核心组成部分。 - 涵义与指称的区分:在 1892 年的论文《论涵义与指称》(Über Sinn und Bedeutung)中,弗雷格区分了语言表达式的“涵义”(Sinn,即认知意义或呈现方式)与“指称”(Bedeutung,即表达式所指代的对象或真值)。例如,“晨星”与“昏星”具有不同的涵义,但指代同一对象(金星)。这一区分澄清了逻辑与语言中的诸多问题,例如同一性陈述(如“长庚星是启明星”)为何能够传递新信息。
- 逻辑主义纲领:弗雷格的核心目标是将数学还原为逻辑(这一纲领被称为“逻辑主义”)。在《算术基础》(1884)与《算术的基本规律》(1893–1903)中,他试图从逻辑公理与定义出发推导出算术(如自然数的定义)。尽管伯特兰·罗素在 1901 年发现的悖论揭示了弗雷格系统的缺陷(其第五公理导致矛盾),但逻辑主义纲领仍影响了罗素、阿尔弗雷德·诺思·怀特海等人的后续研究,并为数理逻辑作为一门基础学科奠定了基础。
- 形式语言与公理系统:弗雷格设计了一套具有精确语法与语义的形式语言(《概念文字》),旨在避免自然语言的模糊性。他还为逻辑构建了公理系统,包含明确的公理与推理规则,为形式系统的严谨性树立了标准。这一方法影响了后续逻辑、数学与计算机科学中形式语言的发展(如编程语言、形式规格说明语言)。
9 Summary
9 总结
This chapter gave a short introduction to logic, and logic is concerned with reasoning and with establishing the validity of arguments. It allows conclusions to be deduced from premises according to logical rules, and the logical argument establishes the truth of the conclusion provided that the premises are true. 本章对逻辑进行了简要介绍。逻辑研究推理及论证有效性的建立,允许根据逻辑规则从前提推导出结论,且若前提为真,逻辑论证可确立结论的真实性。
The origins of logic are with the Greeks who were interested in the nature of truth. Socrates had a reputation for demolishing an opponent’s position (it meant that he did not win any friends with in debate), and the Socratean enquiry consisted of questions and answers in which the opponent would be led to a conclusion incompatible with his original position. His approach was similar to a reductio ad absurdum argument, and its effect was to show that his opponent’s position was incoherent and untenable. 逻辑的起源可追溯至对真理本质感兴趣的古希腊人。苏格拉底以推翻对手的观点而闻名(这意味着他在辩论中并未赢得朋友),苏格拉底问答法通过一连串提问与回答,引导对手得出与其原始立场相矛盾的结论。这种方法类似于归谬法论证,其作用是揭示对手的立场不一致且站不住脚。
Aristotle did important work on logic, and he developed a system of logic, syllogistic logic, that remained in use up to the nineteenth century. Syllogistic logic is a “term-logic”, with letters used to stand for the individual terms. A syllogism consists of two premises and a conclusion, where the conclusion is a valid deduction from the two premises. The Stoics developed an early form of propositional logic, where the assertibles (propositions) have a truth-value such that at any time they are either true or false. 亚里士多德在逻辑领域做出了重要贡献,他发展了一套名为三段论逻辑的体系,该体系一直沿用至 19 世纪。三段论逻辑是一种“词项逻辑”,用字母代表各个词项,由两个前提和一个结论组成,结论是从两个前提中有效推导得出的。斯多葛学派发展了早期的命题逻辑,其中可断言句(命题)具有真值,即在任何时刻要么为真,要么为假。
George Boole developed his symbolic logic in the mid-1800s, and it later formed the foundation for digital computing. Boole argued that logic should be considered as a separate branch of mathematics, rather than a part of philosophy. He argued that there are mathematical laws to express the operation of reasoning in the human mind, and he showed how Aristotle’s syllogistic logic could be reduced to a set of algebraic equations. 乔治·布尔于 19 世纪中叶创立了符号逻辑,该逻辑后来成为数字计算的基础。布尔认为,逻辑应被视为数学的一个独立分支,而非哲学的一部分。他提出,存在数学定律可表达人类思维中的推理过程,并展示了如何将亚里士多德的三段论逻辑简化为一组代数方程。
Gottlob Frege made important contributions to logic and to the foundations of mathematics. He attempted to show that all of the basic truths of mathematics (or at least of arithmetic) could be derived from a limited set of logical axioms (this approach is known as logicism). He invented predicate logic and the universal and existential quantifiers, and predicate logic was a significant advance on Aristotle’s syllogistic logic. 戈特洛布·弗雷格对逻辑和数学基础研究做出了重要贡献。他试图证明所有数学基本真理(至少是算术真理)都可从一组有限的逻辑公理推导而来(这种方法被称为逻辑主义)。他创立了谓词逻辑以及全称量词和存在量词,谓词逻辑是对亚里士多德三段论逻辑的重大突破。
References
参考文献
门电路简称和图形符号
icmaxwell posted @ 2023-05-05 17:12
一、逻辑门限定符号含义
- 符号“≥1”对应「或」逻辑,输出激活的条件为至少一个输入信号处于激活状态。
- 符号“=1”对应「异或」逻辑,输出激活的条件为有且仅有一个输入信号处于激活状态。
- 符号“=”对应「同或」逻辑,输出激活的条件为两个输入信号状态相同。
- 符号“1”本身不对应「非」逻辑,需添加修饰符号后方可表示非逻辑功能;单独符号“1”表示唯一输入信号必须处于激活状态。
- 限定符号与逻辑功能的对应关系:“≥1”对应“或”、“1”(带修饰)对应“非”、“=”对应“同或”、“=1”对应“异或”。
二、逻辑门术语
| 与 | and |
| 或 | or |
| 非 | not |
| 与非 | nand |
| 或非 | nor |
| 同或 | xnor |
| 异或 | xor |
| 双向传输门 | pass |
| 三态门 | tri-pass |
| 缓冲器 | buf |
三、缓冲器与特殊状态表述(Verilog 语法规范)
- 高电平:buf(Y, 1'b1);
- 低电平:buf(Y, 1'b0);
- 高阻态:buf(Y, 1'bz);
四、其他相关电路元件
- 延迟逻辑:delay-cell
- 锁存器:latch
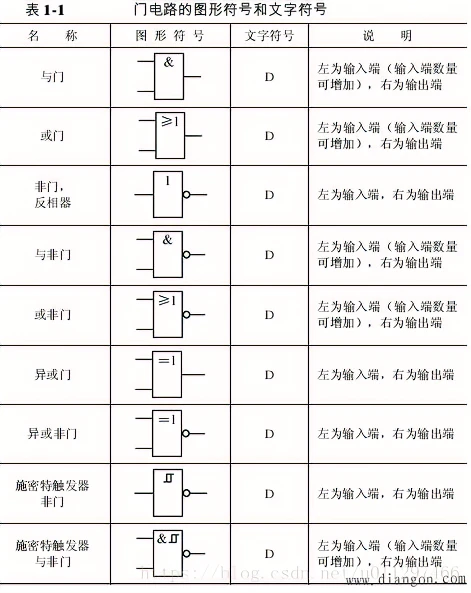
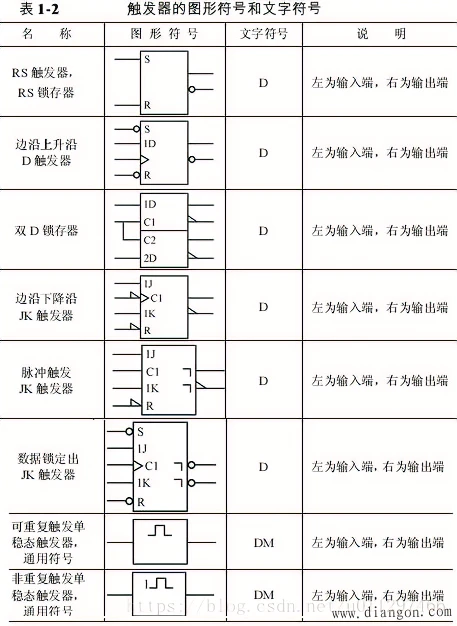
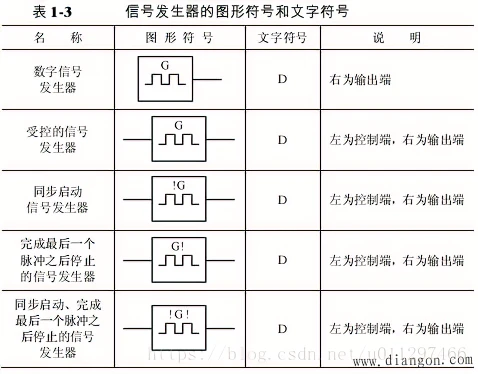
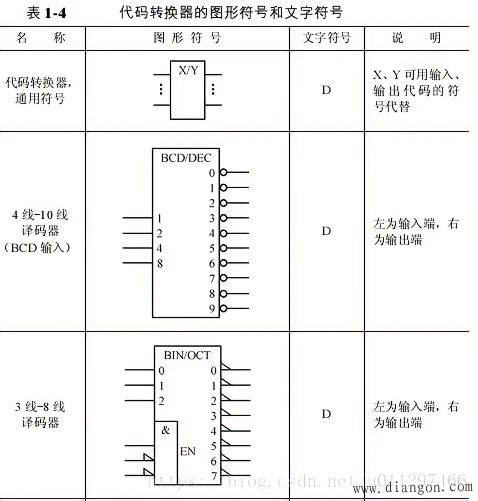
五、基本逻辑门电路图形符号
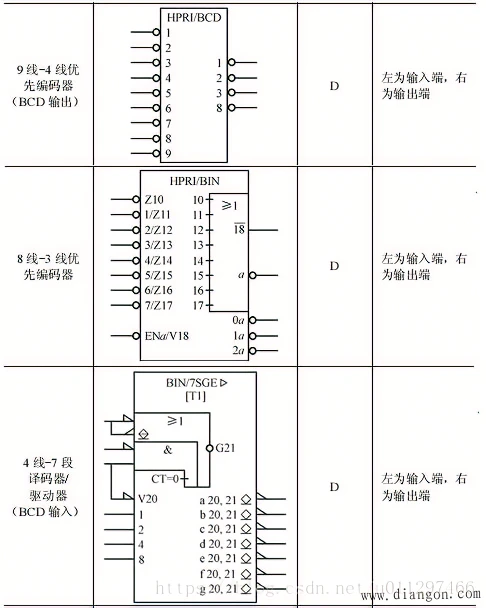
表 C1 列出基本逻辑门电路的国际图形符号和限定符号(依据 GB/T 4728.12-1996 标准)、国外流行图形符号及曾用图形符号。
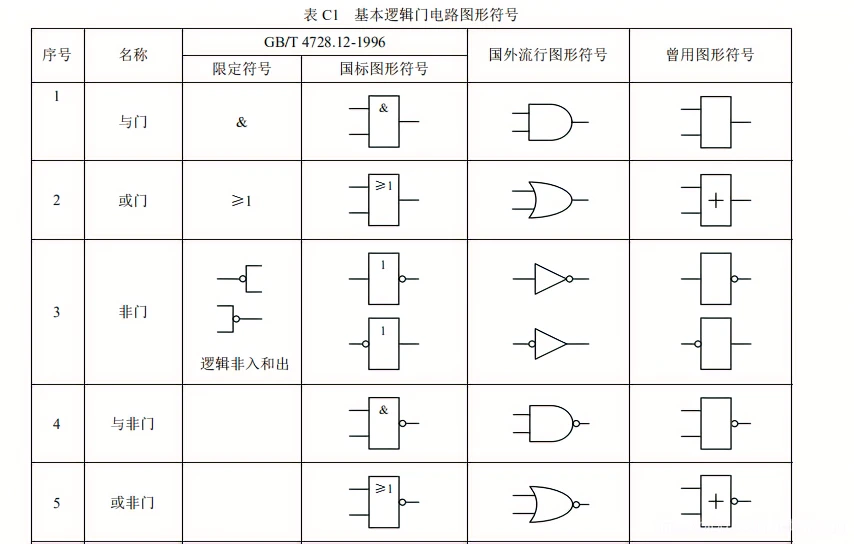
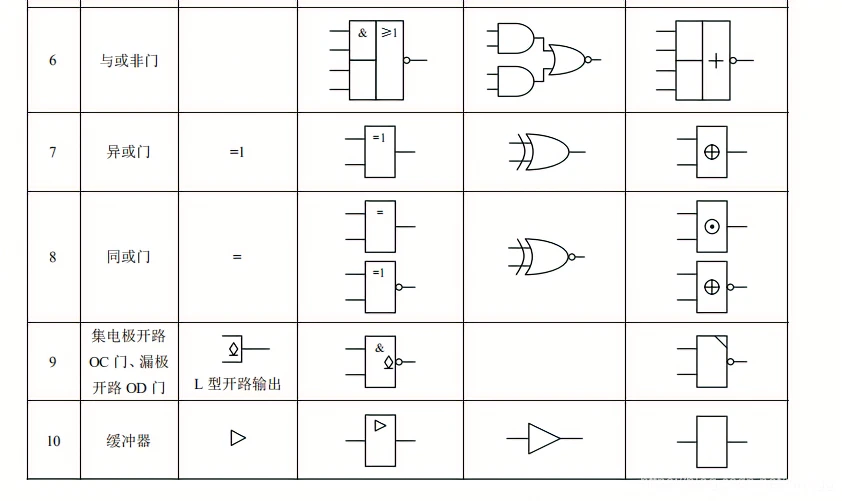
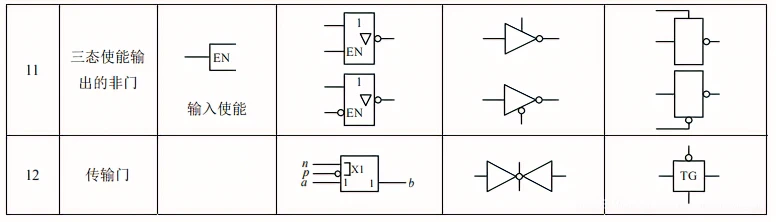
注
表中第三列列出各类限定符号,限定符号包含总限定符号、输入/输出限定符号、内部连接符号、方框内符号、非逻辑连接符号及信息流指示符号等。
- 总限定符号用于表征逻辑单元的整体逻辑功能;
- 输入/输出限定符号标注在逻辑单元方框的输入端或输出端,用于说明输入或输出端口的功能属性;
- 其他类型限定符号分别用于表述逻辑单元内部连接方式、方框内功能模块标识、非逻辑关系连接及信号流向指示等。
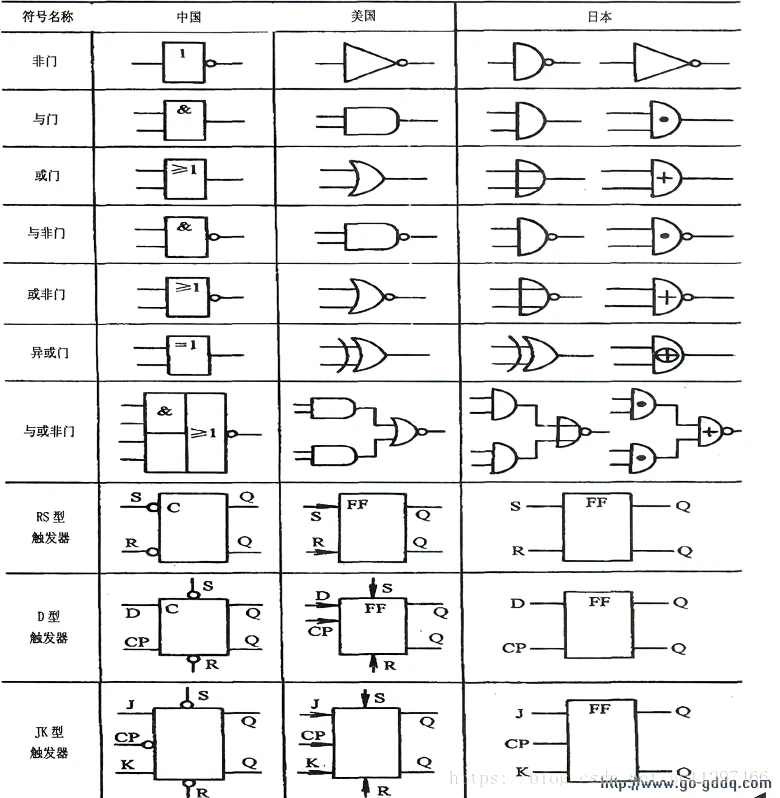
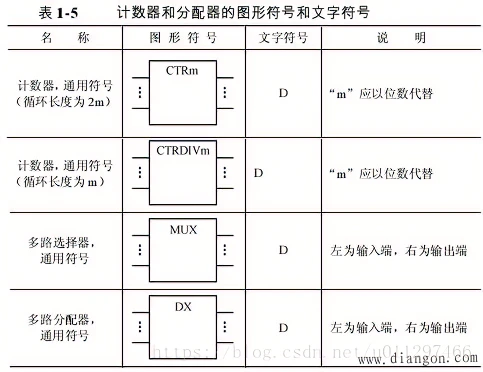





同或运算的逻辑表达式
F
=
A
⊙
B
=
A
⋅
B
+
A
′
⋅
B
′
=
(
A
⊕
B
)
′
F = A \\odot B = A \\cdot B + A' \\cdot B' = (A \\oplus B)'
F=A⊙B=A⋅B+A′⋅B′=(A⊕B)′ (其中
⊙
\\odot
⊙ 为“同或”运算符)
异或运算的逻辑表达式
F
=
A
⊕
B
=
A
⋅
B
′
+
A
′
⋅
B
F = A \\oplus B = A \\cdot B' + A' \\cdot B
F=A⊕B=A⋅B′+A′⋅B (其中
⊕
\\oplus
⊕ 为“异或”运算符)
EOF
七种常见逻辑门及布尔运算规则
一、逻辑电路与逻辑门基础
逻辑门电路(简称“逻辑门”)是实现布尔运算的基本单元,是构成数字逻辑电路的重要组件。其本质是通过特定电路结构响应离散二进制信号(高/低电平),当输入信号满足预设逻辑关系时输出对应电平,反之则输出相反电平,最终完成数字信号的逻辑运算与处理。
由逻辑门构成的逻辑电路,按功能特征可分为两类:
组合逻辑电路:仅由与门、或门、非门等基本逻辑门构成,无反馈回路,输出仅由输入变量的当前值决定,不具备记忆和存储功能,典型如编码器、译码器等。
时序逻辑电路:以基本逻辑门为基础,搭配反馈回路及存储元件(如触发器),输出既依赖输入变量的当前值,也依赖输入变量的过去值,具备记忆特性,典型如寄存器、计数器等。
逻辑电路仅区分高、低两种电平,抗干扰能力强、运算精度高且数据保密性好,是数字电子技术的重要基础,其应用场景已渗透到电子信息领域的方方面面。
计算机中的逻辑运算本质是布尔运算,七种基本布尔运算与七种逻辑门一一对应;布尔值仅包含两个取值,
0
0
0 表示假值(False,对应低电平),
1
1
1 表示真值(True,对应高电平)。七种布尔运算中,仅逻辑非为一元运算(单操作数),其余均为二元运算(双操作数)。
1.1 逻辑门的实现方式
逻辑门的实现依赖半导体器件的开关特性,随着半导体技术发展,实现方式逐步迭代,主流可分为三类:
分立元件实现:早期逻辑门通过真空管、晶体管(三极管)、二极管等分立半导体元件搭建,电路结构松散、体积大、功耗高,仅用于早期电子设备(如第一代计算机),目前已基本淘汰。
集成电路实现:这是当前主流实现方式。通过半导体制造工艺,将多个逻辑门集成在单块芯片上,按集成度可分为小规模集成电路(SSI,含
1
1
1~
10
10
10 个逻辑门)、中规模集成电路(MSI,含
10
10
10~
100
100
100 个逻辑门)及大规模/超大规模集成电路(LSI/VLSI,含上千至上亿个逻辑门),典型如 CPU、FPGA 芯片。
特定工艺实现:针对不同场景需求,采用专用半导体工艺实现,主流包括 TTL(晶体管-晶体管逻辑)和 CMOS(互补金属氧化物半导体)工艺。TTL 门速度快、驱动能力强,曾广泛用于工业控制;CMOS 门功耗极低、抗干扰性更优,是目前民用电子设备(手机、电脑、家电)的主流选择。本文提及的逻辑门电路示意图均为 CMOS 工艺实现。
1.2 逻辑门的发展历程
逻辑门的发展与半导体技术、电子计算技术的迭代深度绑定,大致可分为四个阶段:
真空管时代(20 世纪 40 年代):全球首个逻辑门由真空管实现,用于 ENIAC 等第一代计算机。此时的逻辑门体积庞大、功耗极高、稳定性差,限制了电子设备的小型化发展。
晶体管时代(20 世纪 50 年代):晶体管逐步替代真空管,逻辑门的体积、功耗大幅降低,稳定性显著提升,推动了第二代计算机的普及,也为集成电路的出现奠定了基础。
集成电路时代(20 世纪 60 年代至今):1958 年集成电路发明后,逻辑门进入集成化发展阶段。从最初的小规模集成,到后来的大规模、超大规模集成,单块芯片上的逻辑门数量呈指数级增长,促成了微型计算机、智能手机等设备的诞生,成为数字技术革命的重要驱动力。
先进工艺时代(21 世纪以来):随着半导体工艺节点不断突破,逻辑门的运算速度更快、功耗更低、集成度更高,支撑了人工智能、云计算、量子计算等前沿领域的发展,同时也朝着低功耗、高可靠性、异构集成的方向演进。
1.3 逻辑门的应用领域
逻辑门作为数字电路的基础单元,其应用覆盖所有电子信息领域,场景包括:
计算机领域:CPU、GPU、内存、芯片组等重要部件,均由海量逻辑门组合构成,负责运算、控制、数据存储与传输,是计算机实现计算功能的重要支撑。
通信领域:光纤通信、无线通信设备中的信号编码、解码、调制、解调模块,通过逻辑门实现信号处理与逻辑控制,保障数据传输的准确性与高效性。
工业控制领域:PLC(可编程逻辑控制器)、传感器、伺服驱动器等设备,利用逻辑门构建控制电路,实现对工业生产流程的自动化控制、精准调节与故障检测。
消费电子领域:智能手机、家电、智能穿戴设备等,其主控芯片中的逻辑门负责处理用户操作、图像显示、电源管理等功能,是设备实现智能化的基础。
前沿科技领域:量子计算机、人工智能芯片、航空航天电子设备等,通过定制化逻辑门结构,满足高运算速度、高可靠性、抗辐射等特殊需求,推动科技领域的突破。
二、七种常见逻辑门的运算规则与真值表
七种基本逻辑门分为两类:基本逻辑门(与门、或门、非门)和复合逻辑门(与非门、或非门、异或门、同或门),复合逻辑门可由基本逻辑门组合实现。
2.1 与门(AND)
-
运算规则:全
1
1
1 为
1
1
1,有
0
0
0 为
0
0
0(仅当所有输入均为高电平时,输出才为高电平;任意输入为低电平,输出均为低电平)。
-
逻辑函数表达式:
Y
=
A
∧
B
Y = A \\land B
Y=A∧B
-
等效逻辑表达式:
Y
=
A
⋅
B
Y = A \\cdot B
Y=A⋅B
-
CMOS 电路示意图:

-
真值表:
|
0 0 0 |
0 0 0 |
0 0 0 |
|
0 0 0 |
1 1 1 |
0 0 0 |
|
1 1 1 |
0 0 0 |
0 0 0 |
|
1 1 1 |
1 1 1 |
1 1 1 |
2.2 或门(OR)
-
运算规则:全
0
0
0 为
0
0
0,有
1
1
1 为
1
1
1(仅当所有输入均为低电平时,输出才为低电平;任意输入为高电平,输出均为高电平)。
-
逻辑函数表达式:
Y
=
A
∨
B
Y = A \\lor B
Y=A∨B
-
等效逻辑表达式:
Y
=
A
+
B
Y = A + B
Y=A+B
-
CMOS 电路示意图:

-
真值表:
|
0 0 0 |
0 0 0 |
0 0 0 |
|
0 0 0 |
1 1 1 |
1 1 1 |
|
1 1 1 |
0 0 0 |
1 1 1 |
|
1 1 1 |
1 1 1 |
1 1 1 |
2.3 非门(NOT)
-
运算规则:
1
1
1 变
0
0
0,
0
0
0 变
1
1
1(仅一个输入端,逆转输入信号的高低电平状态,又称“反相器”)。
-
逻辑函数表达式:
Y
=
¬
A
Y = \\neg A
Y=¬A
-
等效逻辑表达式:
Y
=
A
‾
Y = \\overline{A}
Y=A
-
CMOS 电路示意图:

-
真值表:
|
0 0 0 |
1 1 1 |
|
1 1 1 |
0 0 0 |
2.4 与非门(NAND)
-
运算规则:先与后非(对两个输入信号执行与运算,再对运算结果取非;即所有输入为高电平时输出低电平,其余情况输出高电平)。
-
逻辑函数表达式:
Y
=
¬
(
A
∧
B
)
Y = \\neg (A \\land B)
Y=¬(A∧B)
-
等效逻辑表达式:
Y
=
A
⋅
B
‾
Y = \\overline{A \\cdot B}
Y=A⋅B
-
真值表:
|
0 0 0 |
0 0 0 |
1 1 1 |
|
0 0 0 |
1 1 1 |
1 1 1 |
|
1 1 1 |
0 0 0 |
1 1 1 |
|
1 1 1 |
1 1 1 |
0 0 0 |
2.5 或非门(NOR)
-
运算规则:先或后非(对两个输入信号执行或运算,再对运算结果取非;即所有输入为低电平时输出高电平,其余情况输出低电平)。
-
逻辑函数表达式:
Y
=
¬
(
A
∨
B
)
Y = \\neg (A \\lor B)
Y=¬(A∨B)
-
等效逻辑表达式:
Y
=
A
+
B
‾
Y = \\overline{A + B}
Y=A+B
-
真值表:
|
0 0 0 |
0 0 0 |
1 1 1 |
|
0 0 0 |
1 1 1 |
0 0 0 |
|
1 1 1 |
0 0 0 |
0 0 0 |
|
1 1 1 |
1 1 1 |
0 0 0 |
2.6 异或门(XOR)
-
运算规则:相异为
1
1
1,相同为
0
0
0(两个输入信号电平不同时输出高电平,电平相同时输出低电平)。
-
逻辑函数表达式:
Y
=
A
⊕
B
Y = A \\oplus B
Y=A⊕B
-
等效逻辑表达式:
Y
=
A
⋅
B
‾
+
A
‾
⋅
B
Y = A \\cdot \\overline{B} + \\overline{A} \\cdot B
Y=A⋅B+A⋅B
-
真值表:
|
0 0 0 |
0 0 0 |
0 0 0 |
|
0 0 0 |
1 1 1 |
1 1 1 |
|
1 1 1 |
0 0 0 |
1 1 1 |
|
1 1 1 |
1 1 1 |
0 0 0 |
2.7 同或门(XNOR)
-
运算规则:相同为
1
1
1,相异为
0
0
0(两个输入信号电平相同时输出高电平,电平不同时输出低电平;与异或门运算结果互为非值,又称“异或非门”)。
-
逻辑函数表达式:
Y
=
¬
(
A
⊕
B
)
Y = \\neg (A \\oplus B)
Y=¬(A⊕B)
-
等效逻辑表达式:
Y
=
A
⋅
B
+
A
‾
⋅
B
‾
Y = A \\cdot B + \\overline{A} \\cdot \\overline{B}
Y=A⋅B+A⋅B
-
真值表:
|
0 0 0 |
0 0 0 |
1 1 1 |
|
0 0 0 |
1 1 1 |
0 0 0 |
|
1 1 1 |
0 0 0 |
0 0 0 |
|
1 1 1 |
1 1 1 |
1 1 1 |
三、七种逻辑门表达式汇总表
| 与门 (AND) |
∧ \\land ∧ |
Y = A ∧ B Y = A \\land B Y=A∧B |
Y = A ⋅ B Y = A \\cdot B Y=A⋅B |
| 或门 (OR) |
∨ \\lor ∨ |
Y = A ∨ B Y = A \\lor B Y=A∨B |
Y = A + B Y = A + B Y=A+B |
| 非门 (NOT) |
¬ \\neg ¬ |
Y = ¬ A Y = \\neg A Y=¬A |
Y = A ‾ Y = \\overline{A} Y=A |
| 与非门 (NAND) |
∧ ‾ \\overline{\\land} ∧ |
Y = ¬ ( A ∧ B ) Y = \\neg (A \\land B) Y=¬(A∧B) |
Y = A ⋅ B ‾ Y = \\overline{A \\cdot B} Y=A⋅B |
| 或非门 (NOR) |
∨ ‾ \\overline{\\lor} ∨ |
Y = ¬ ( A ∨ B ) Y = \\neg (A \\lor B) Y=¬(A∨B) |
Y = A + B ‾ Y = \\overline{A + B} Y=A+B |
| 异或门 (XOR) |
⊕ \\oplus ⊕ |
Y = A ⊕ B Y = A \\oplus B Y=A⊕B |
Y = A ⋅ B ‾ + A ‾ ⋅ B Y = A \\cdot \\overline{B} + \\overline{A} \\cdot B Y=A⋅B+A⋅B |
| 同或门 (XNOR) |
⊕ ‾ \\overline{\\oplus} ⊕(或 ⊙ \\odot ⊙) |
Y = ¬ ( A ⊕ B ) Y = \\neg (A \\oplus B) Y=¬(A⊕B) |
Y = A ⋅ B + A ‾ ⋅ B ‾ Y = A \\cdot B + \\overline{A} \\cdot \\overline{B} Y=A⋅B+A⋅B |
四、逻辑门特征总结
逻辑门是数字逻辑电路的最小功能单元,所有复杂数字电路(从简单控制器到超大规模集成电路)均可通过七种基本逻辑门组合实现。
运算特性区分明确:一元运算仅逻辑非一种,无需组合输入;二元运算需两个输入信号配合,输出由输入组合关系唯一确定,无歧义。
复合逻辑门可由基本逻辑门推导组合:与非门 = 与门 + 非门,或非门 = 或门 + 非门,异或门、同或门可由与门、或门、非门组合实现;其中与非门和或非门为通用逻辑门,无需依赖其他逻辑门即可组合实现任意逻辑功能,在集成电路设计中应用最广。
互补关系明确:异或门与同或门运算结果互为非值,即
A
⊙
B
=
¬
(
A
⊕
B
)
A \\odot B = \\neg (A \\oplus B)
A⊙B=¬(A⊕B)(
⊙
\\odot
⊙ 为同或专用运算符,与
⊕
‾
\\overline{\\oplus}
⊕ 完全等效)。
逻辑门整体特征示意图:

- 数字电路 · 逻辑门 | 图解 / 真值表-CSDN博客 https://blog.csdn.net/u013669912/article/details/151874793
via:
-
From Ancient Binary to Silicon Chips: Logic Through History – Industry Articles https://www.allaboutcircuits.com/industry-articles/from-ancient-binary-to-silicon-chips-logic-through-history/
- False Dawn: The Babbage Engine – YouTube https://www.youtube.com/watch?v=XSkGY6LchJs
-
A Short History of Logic | Springer Nature Link https://link.springer.com/chapter/10.1007/978-3-319-64021-1_5
-
门电路简称和图形符号 – icmaxwell – 博客园 https://www.cnblogs.com/icmaxwell/p/17374702.html
-
Logic gate | Wikitronics | Fandom https://electronics.fandom.com/wiki/Logic_gate
-
零基础学习计算机原理:布尔逻辑和逻辑门 – 知乎 https://zhuanlan.zhihu.com/p/151043418
-
布尔逻辑 和 逻辑门-Boolean Logic & Logic Gates_哔哩哔哩_bilibili https://www.bilibili.com/video/BV1EW411u7th/?p=3
 网硕互联帮助中心
网硕互联帮助中心

![[特殊字符]BZOJ 离线刷题神级工具!免联网 + 浏览器即开 + 题解代码全,效率直接翻倍!-网硕互联帮助中心](https://www.wsisp.com/helps/wp-content/uploads/2026/01/20260125122457-69760b9998bf0-220x150.png)




评论前必须登录!
注册