机器学习————梯度提升树

        梯度提升树（GBDT）是在函数空间中通过梯度下降法串行训练多棵回归决策树，每棵新树拟合当前模型损失函数的负梯度，并通过学习率控制每棵树的贡献权重，最终将所有树的预测结果加权累加，以逐步最小化损失函数的集成学习算法。

一、核心概念

提升（Boosting）

        定义：串行训练多个弱学习器（如决策树），每一个新学习器都修正前一个的错误，最终集成所有学习器的结果。

弱学习器

        定义：性能略优于随机猜测的简单模型，并且GBDT 中固定为回归决策树。

        作用：单棵树拟合能力弱，但多棵树累加后形成强学习器。

残差

        定义：真实值 – 模型当前预测值。

        作用：平方损失下，残差等价于损失函数的负梯度。

梯度提升

        定义：用梯度下降思想优化损失函数，每一轮沿损失函数的负梯度方向训练新弱学习器。

        作用：残差是平方损失的特例，梯度提升是更通用的框架。

学习率

        定义：每棵弱学习器预测结果的权重系数（η）。

        作用：控制每一轮修正的幅度，防止模型过拟合。

二、数学原理

1.计算前提

        设有训练集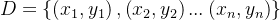,目标是学习一个模型F(x),最小化损失函数。

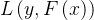GBDT 的最终模型是所有弱学习器的加权和：

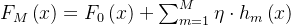
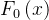• ：初始模型（常数，如标签均值）；
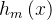• ：第m棵回归决策树（弱学习器）；
• η：学习率（0<η≤1）；
• M：弱学习器的总数。

2. 核心推导步骤

        GBDT 的迭代过程本质是函数空间的梯度下降,普通梯度下降是参数空间的优化，GBDT 是优化函数。

步骤 1：初始化初始模型

初始模型选择使损失函数最小的常数：

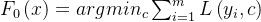
(注：存在平方损失和绝对损失，这里有以平方损失为例)

步骤 2：迭代训练每一棵决策树

1.计算负梯度

        对每个样本i，计算损失函数在当前模型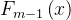处的负梯度，作为第m棵树需要拟合的目标。

公式为：

2.拟合回归决策树

        用训练集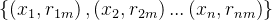  训练一棵回归决策树 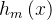hm​(x)，得到树的叶节点划分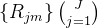,J是叶节点数）。

3.更新叶节点权重

        对每个叶节点j，求解最优权重。

公式为：;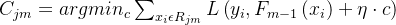

4.更新模型

        将第m棵树的结果加权后加入模型：

;

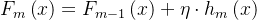步骤 3：终止迭代

        当迭代次数达到M，或损失函数收敛时，停止迭代，得到最终模型 。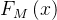

三、代码解释——以回归任务为例

模块一：导入核心库

import numpy as np # 数值计算库，处理数组/矩阵运算
import pandas as pd # 数据处理库，结构化数据管理
import matplotlib.pyplot as plt # 可视化库，绘制图表
# 加载加州房价数据集（替代波士顿房价，解决sklearn版本兼容问题）
from sklearn.datasets import fetch_california_housing
# 划分训练集/测试集，评估模型泛化能力
from sklearn.model_selection import train_test_split
# GBDT回归器核心类（封装了GBDT的全部迭代逻辑）
from sklearn.ensemble import GradientBoostingRegressor
# 回归任务评估指标：MSE(均方误差)、R²(决定系数)
from sklearn.metrics import mean_squared_error, r2_score

模块二：数据准备

# 加载加州房价数据集：返回字典对象，包含特征、标签、特征名等
housing = fetch_california_housing()
# 将特征数组转为DataFrame，指定列名（方便后续特征重要性匹配）
# housing.data: 特征数组(20640,8)；housing.feature_names: 8个特征名称
X = pd.DataFrame(housing.data, columns=housing.feature_names)
# 提取目标变量（房价，单位：10万美元）
y = housing.target

# 划分训练集(70%)/测试集(30%)
# random_state=42：固定随机种子，保证每次划分结果一致（可复现）
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=42
)

模块三：构建GBDT模型

# 初始化GBDT回归器（参数对应GBDT数学原理）
gbdt = GradientBoostingRegressor(
loss='squared_error', # 损失函数：平方损失（回归默认，伪残差=普通残差）
learning_rate=0.1, # 学习率η：每棵树的贡献权重（步长）
n_estimators=100, # 树的数量M：迭代100次（训练100棵回归树）
max_depth=3, # 单棵树最大深度：控制过拟合（GBDT建议3-5）
min_samples_split=2, # 节点分裂最小样本数：<2时停止分裂
random_state=42 # 固定随机种子，保证模型训练过程可复现
)

# 训练模型：底层执行GBDT完整迭代流程
# 1. 初始化F0(x)=训练集标签均值；2. 迭代100次拟合伪残差；3. 累加所有树结果
gbdt.fit(X_train, y_train)

模块四：模型评估

# 用训练好的模型预测训练集/测试集房价
y_train_pred = gbdt.predict(X_train) # 训练集预测值
y_test_pred = gbdt.predict(X_test) # 测试集预测值

# 计算评估指标
# MSE(均方误差)：衡量预测值与真实值的平均平方偏差，越小越好
train_mse = mean_squared_error(y_train, y_train_pred) # 训练集MSE
test_mse = mean_squared_error(y_test, y_test_pred) # 测试集MSE
# R²(决定系数)：衡量模型解释数据变异的能力，越接近1越好（1=完美拟合，0=等价预测均值）
train_r2 = r2_score(y_train, y_train_pred) # 训练集R²
test_r2 = r2_score(y_test, y_test_pred) # 测试集R²

# 格式化打印评估结果（保留4位小数，提升可读性）
print("="*50)
print(f"训练集MSE: {train_mse:.4f} | 训练集R²: {train_r2:.4f}")
print(f"测试集MSE: {test_mse:.4f} | 测试集R²: {test_r2:.4f}")
print("="*50)

模块五：可视化

# ————————– 5. 可视化：训练过程误差变化 ————————–
# 初始化数组：存储每一轮迭代的测试集MSE（长度=100，对应100棵树）
test_score = np.zeros((gbdt.n_estimators,), dtype=np.float64)
# 遍历每一轮迭代的预测结果（staged_predict返回每轮累加后的预测值）
for i, y_pred in enumerate(gbdt.staged_predict(X_test)):
# 计算第i轮的测试集MSE，存入数组
test_score[i] = mean_squared_error(y_test, y_pred)

# 创建画布
plt.figure(figsize=(10, 6))
# 绘制训练集误差曲线（gbdt.train_score_是内置属性，存储每轮训练集MSE）
plt.plot(
np.arange(gbdt.n_estimators) + 1, # x轴：迭代次数（1-100）
gbdt.train_score_, # y轴：训练集每轮MSE
label='训练集MSE', # 图例标签
color='blue' # 曲线颜色
)
# 绘制测试集误差曲线
plt.plot(
np.arange(gbdt.n_estimators) + 1, # x轴：迭代次数（1-100）
test_score, # y轴：测试集每轮MSE
label='测试集MSE', # 图例标签
color='red' # 曲线颜色
)
plt.xlabel('迭代次数（树的数量M）') # x轴标签
plt.ylabel('均方误差（MSE）') # y轴标签
plt.title('GBDT训练过程误差变化') # 图表标题
plt.legend() # 显示图例
plt.grid(alpha=0.3) # 添加网格线（透明度0.3），方便读取坐标
plt.tight_layout() # 自动调整布局
plt.show() # 显示图表

结语

        感谢大家的观看！如有不足请大家的批评指正。