第七章 贝叶斯分类器

7.1贝叶斯决策论

即多分类任务下基于概率和误判损失来选择最优的类别标记。

贝叶斯判定准则：最小化总体条件风险通过最小化每个样本的条件风险来实现。

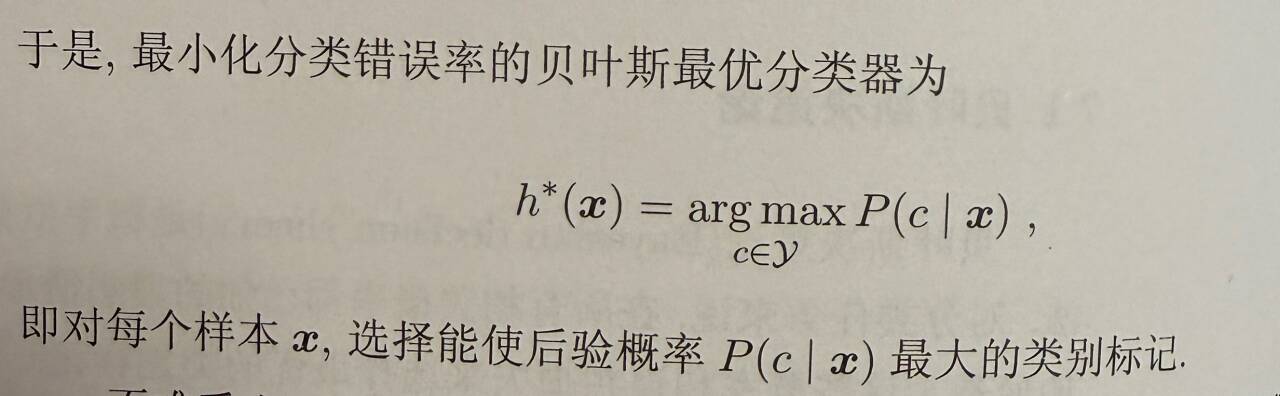
0/1损失函数条件下，P（c|x）后验概率即样本x判断为c正确的概率，此时最大后验概率即最小化总体损失风险，所以等价于将问题化为求最大的后验概率。

判别式模型是根据输入和输出得到模型；生成式模型是根据联合概率分布得到条件概率，进而还能预测新样本。

7.2极大似然估计

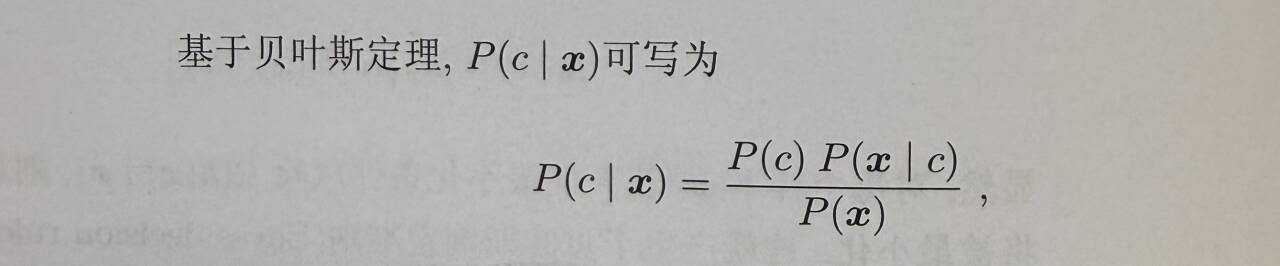
后验概率由贝叶斯变成P（x|c），后等价写为P（x|θ），这里x表示样本特征，θ表示类别（好、坏）。举例子说明一下过程！！

最大似然估计的核心就是：把似然函数当作目标函数，通过调整模型里的未知参数，找到能让这个目标函数取值最大的参数值。

简单说，就是“找参数，让观测数据的出现概率最大”，本质就是一个目标函数的最大化优化问题。

7.3朴素贝叶斯分类器

其实也就是属性拆分的意思，把多个属性联合概率拆分为相互独立的多个条件概率。

这里拉普拉斯修正是辅助计算正确的，避免朴素贝叶斯计算时因为某个属性概率为0的问题，通常使条件概率的分子分母都有一个很小的基础数。

7.4半朴素贝叶斯分类器

适当考虑一部分的相互依赖信息，保留一部分依赖比较强的依赖。

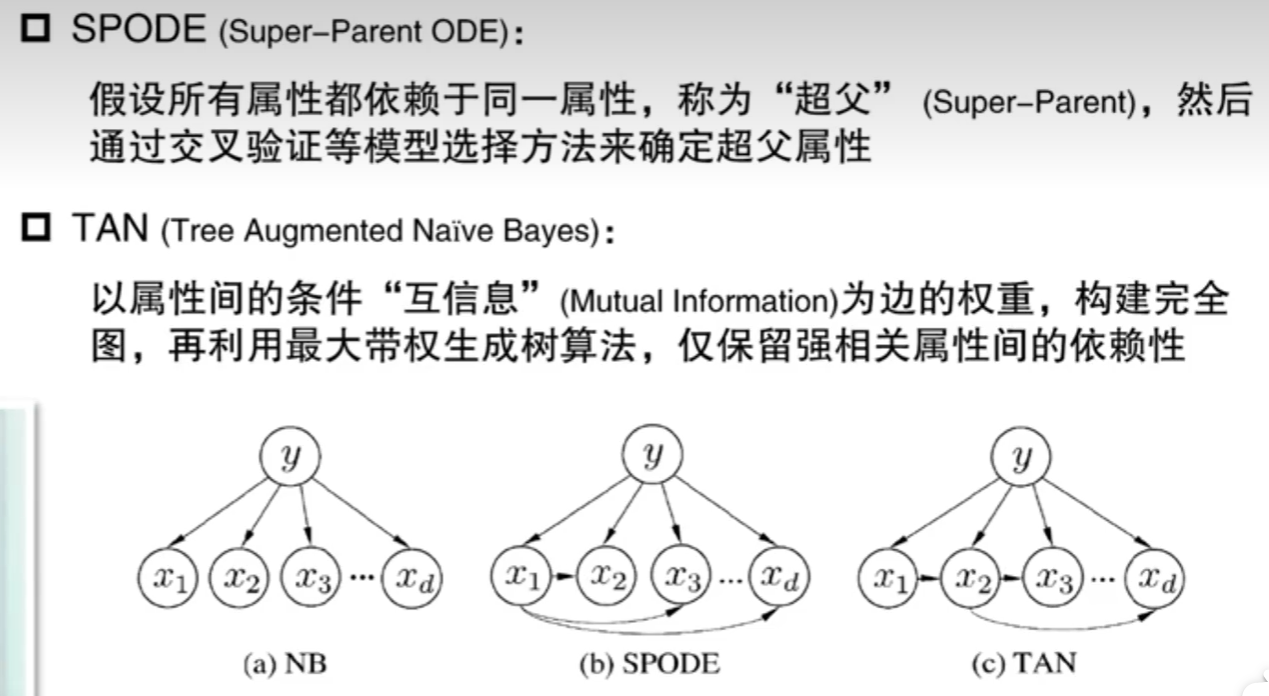
第二个TAN是指先生成一个贝叶斯图，然后提取一棵生成树出来。

第三个并不是所有属性都能作为超父来构建有效模型——AODE会设置一个样本数量阈值，只有当以某属性 x_i 为超父时，其对应的训练样本数（即满足 x_i 取值的样本数）超过阈值，这个属性才会被选为超父，基于它构建的SPDE模型才会被纳入后续的平均计算中。AODE会把所有符合阈值条件的SPDE模型的预测结果做平均，以此降低单模型的偏差，提升分类稳定性。

7.5贝叶斯网

定义：借助有向无环图来刻画属性间的依赖关系，并用条件概率描述分布。

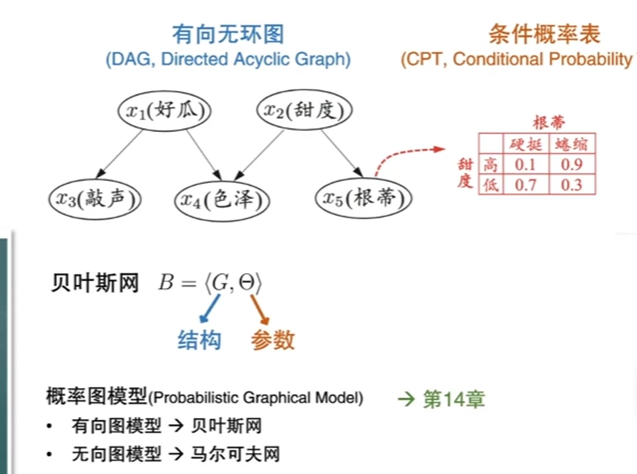
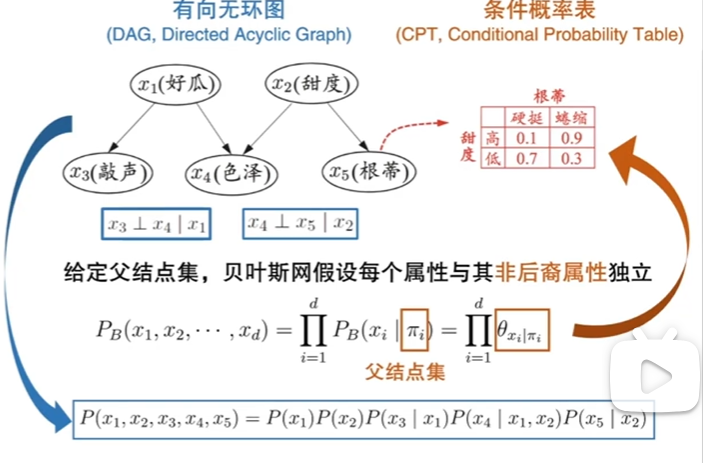
概率图模型中有向图相较于无向图更复杂在需要确定方向，推理出因果关系。

由有向无环图推出联合概率，得到的联合概率是通过链式法则化简得到的。

7.5.1结构

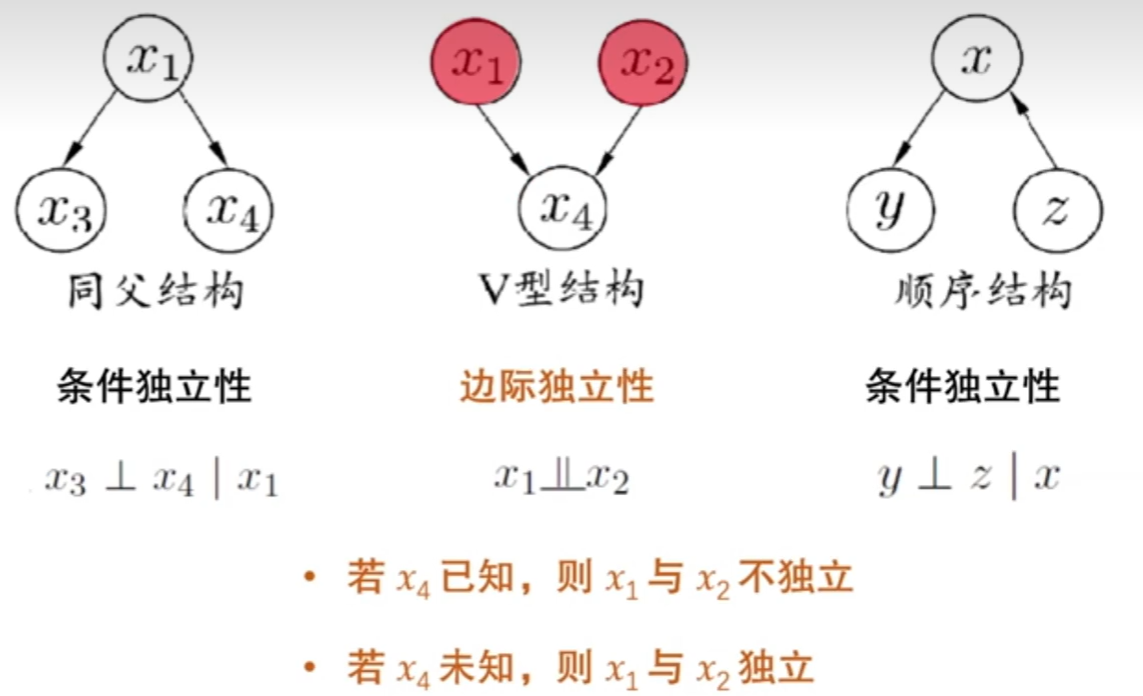
分别表示为x1已知条件下，x3与x4独立。

7.5.2学习

找到最契合数据集的贝叶斯网结构，需要使用到评分函数，此处MDL越小越好。

下图更好理解前项-后项的表达式，前项代表存储模型需要的数据，后项代表模型未契合数据，额外需要的存储内容。

7.5.3推断

推断：它不是“部分猜测”，而是基于已知的观测变量（真实值），利用贝叶斯网的联合概率分布和条件独立性，精确计算或近似估算目标变量的后验概率分布的过程。

先验不是“猜”，是无本次观测证据时的初始概率（可以是无条件概率，也可以是基于模型结构的条件概率）；后验是加入本次观测证据后，用概率规则计算出的修正概率（一定是条件概率）。

7.8EM算法

EM 算法不是直接转化 LL(θ|X)，而是通过引入隐变量 Z 构造证据下界（ELBO），把“直接最大化 LL(θ|X)”这个难求解的问题，转化为“迭代最大化 ELBO”的易求解问题——且每一轮迭代都会让 LL(θ|X) 单调上升，最终收敛到它的局部最大值。