题目描述
输入一个偶数 N,验证 4∼N 所有偶数是否符合哥德巴赫猜想:任一大于 2 的偶数都可写成两个质数之和。如果一个数不止一种分法,则输出第一个加数相比其他分法最小的方案。例如 10,10=3+7=5+5,则 10=5+5 是错误答案。
输入格式
第一行输入一个正偶数 N
输出格式
输出 2N−2 行。对于第 i 行:
首先先输出正偶数 2i+2,然后输出等号,再输出加和为 2i+2 且第一个加数最小的两个质数,以加号隔开。
输入输出样例
输入 #1复制运行
10
输出 #1复制运行
4=2+2
6=3+3
8=3+5
10=3+7
说明/提示
数据保证,4≤N≤10000。
在算法竞赛中,素数筛法是数论题目的基石。本文将以洛谷哥德巴赫猜想验证为例,深入拆解两种核心筛法:埃氏筛与欧拉筛,并用表格演示它们是如何工作的。
0. 题目核心
-
目标:验证4–N的偶数是否符合“任意大于2的偶数=两个质数之和”。
-
难点:N=10000虽然不大,但在验证时需要频繁判断一个数是否为素数。如果每次都循环判断,效率太低。我们需要预处理出一个素数表。
1. 方法一:埃氏筛法 (Sieve of Eratosthenes)
这是最直观的“划圈法”。
核心逻辑(文本演示)
想象一个从2到N的数字列表。
第一轮:找到第一个没被划掉的数2(它是素数)。然后把所有2的倍数(4, 6, 8, 10…)全部划掉(标记为合数)。
第二轮:下一个没被划掉的数是3(它是素数)。把所有3的倍数(6, 9, 12, 15…)全部划掉。
-
注意6在第一轮已经被2划过了,这里又被3划了一次。这就是效率损耗点。
第三轮:4已经被划掉了,跳过。下一个是5…
结束:一直操作到 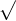 N 为止。
N 为止。
代码实现
void esieve(){
//0和1不是素数,手动初始化
es[0]=1;
es[1]=1;
for(int i=2;i<=n/i;i++){
//如果es[i]是0,代表i是素数
if(es[i]==0){
//既然i是素数,那么i的倍数(2倍、3倍…)肯定就是合数。
//j代表倍数。只要i*j还在范围n以内,我们就一个个标记。
for(int j=2;j<=n/i;j++)
es[i*j]=1;
}
}
}
2. 方法二:欧拉筛 (Euler Sieve / 线性筛)
欧拉筛是为了解决埃氏筛“重复标记”的问题(比如6既被2筛,又被3筛)。
核心法则:每个合数,只被它“最小”的质因子筛掉。
算法步骤拆解
我们需要两个数组:
-
es[]: 标记是否为合数。
-
prime[]: 存目前找到的素数。
对于每一个数 i (从2到N):
如果 i 是素数,加入prime表。
(关键步骤) 遍历当前已有的素数prime[j]:
-
标记i*prime[j] 为合数。
-
停止条件:如果i%prime[j]==0,立刻break停止循环。
为什么需要 break?(模拟执行表)
这是欧拉筛最难懂的地方。让我们通过表格来看看,如果不加break会发生什么,加了又会怎样。
假设我们要筛的范围稍大一点,当前遍历到 i=4。
此时素数表 prime 里有:[2, 3]。
| 步骤 | 当前数 i | 遍历素数 prime[j] | 筛掉的数 (i * prime[j]) | 关键判断 (i%prime[j]==0?) | 结果 |
| 1 | 4 | 2 | 筛掉 8 (4*2) | 4%2==0 (成立) | Break! 退出循环 |
| (假设无Break) | 4 | 3 | 筛掉 12 (4*3) | – | (这步被优化掉了) |
深度解析:
-
我们筛掉了 8。8 的最小质因子是 2。
-
如果我们继续,会筛掉 12 (4*3)。
-
但是,12的最小质因子其实是 2 (12=2*6)。
-
根据欧拉筛的法则“只由最小质因子筛掉”,12 应该在未来当 i=6 的时候,被 2 (6*2) 筛掉。
-
所以,在 i=4 时,一旦发现4%2==0,说明4包含了因子2。那么4乘以任何更大的素数(比如 3, 5…),结果肯定也包含因子 2。为了不抢“2”的工作,我们必须在这里停止。
代码实现
void Prime(){
//外层是倍数
for(int i=2;i<=n;i++){
if(es[i]==0){//如果es[i]是0,代表i是素数
k++;
prime[k]=i;//记录素数
}
//内层总共有k个素数+防止越界
for(int j=1;j<=k && i*prime[j]<=n;j++){
//素数的倍数肯定标记为合数
es[i*prime[j]]=1;
//如果i能被 prime[j]整除,说明 prime[j]是i的最小质因子
// 后面的素数更大,乘积的最小质因子依然是prime[j],留给后面筛,这里跳出
if(i%prime[j]==0) break;
}
}
}
3. 题目解法:寻找最小加数
题目要求:对于偶数N,输出 N=A+B,且 A 是所有方案中最小的。
策略:
外层循环遍历所有偶数i (4到N)。
内层循环直接遍历我们在筛法中生成的prime数组(从小到大)。
对于每个素数p,判断i-p是否也是素数(查es表)。
一旦找到,直接输出并break。因为prime数组本身就是有序的,第一个找到的一定是 A 最小的方案。
4. 完整代码
// //埃氏筛法
// #include <iostream>
// using namespace std;
// int es[10010];//埃氏表 素数为0 非素数为1
// int n;
// void esieve(){
// //0和1不是素数,手动初始化
// es[0]=1;
// es[1]=1;
// for(int i=2;i<=n/i;i++){
// //如果es[i]是0,代表i是素数
// if(es[i]==0){
// //既然i是素数,那么i的倍数(2倍、3倍…)肯定就是合数。
// //j代表倍数。只要i*j还在范围n以内,我们就一个个标记。
// for(int j=2;j<=n/i;j++)
// es[i*j]=1;
// }
// }
// }
// int main(){
// cin>>n;
// //先求出n以内所有素数
// esieve();
// //验证4∼N所有偶数是否符合哥德巴赫猜想
// for(int i=4;i<=n;i=i+2){
// for(int j=2;j<=n/2;j++){
// if(es[j]==0 && es[i-j]==0){
// cout<<i<<"="<<j<<"+"<<i-j<<endl;
// break;
// }
// }
// }
// return 0;
// }
//欧拉筛
#include <iostream>
using namespace std;
int es[10010];//标记数组 (0表示未被筛掉,即素数;1表示非素数)
int prime[10010];//素数表
int k;//记录素数个数
int n;
void Prime(){
//外层是倍数
for(int i=2;i<=n;i++){
if(es[i]==0){//如果es[i]是0,代表i是素数
k++;
prime[k]=i;//记录素数
}
//内层总共有k个素数+防止越界
for(int j=1;j<=k && i*prime[j]<=n;j++){
//素数的倍数肯定标记为合数
es[i*prime[j]]=1;
//如果i能被 prime[j]整除,说明 prime[j]是i的最小质因子
// 后面的素数更大,乘积的最小质因子依然是prime[j],留给后面筛,这里跳出
if(i%prime[j]==0) break;
}
}
}
int main(){
cin>>n;
Prime();
//for(int i=1;i<=k;i++) cout<<prime[i]<<" ";
for(int i=4;i<=n;i=i+2){
for(int j=1;j<=k;j++){
if(es[i-prime[j]]==0){
cout<<i<<"="<<prime[j]<<"+"<<i-prime[j]<<endl;
break;
}
}
}
}
5. 总结对比
| 特性 | 埃氏筛 (Eratosthenes) | 欧拉筛 (Euler) |
| 原理 | 暴力划掉所有倍数 | 仅通过最小质因子划掉合数 |
| 效率 | 稍慢 (有重复操作) | 最快 (线性O(N)) |
| 代码难度 | 简单直观 | 需要理解break的数学含义 |
| 本题推荐 | 完全够用 | 最佳效率 |
 网硕互联帮助中心
网硕互联帮助中心


评论前必须登录!
注册