电路传递函数建模及优化

方法一：

把输入节点到地的连接等效成一整个阻抗，利用输出节点到地的连接等效成另一个阻抗，通过两个阻抗串联分压关系来求传递函数，适用于一些简单的电路。

以桑森书上第24章P542-P543中RLC串联谐振电路减小键合电感导致的电源波动为例：

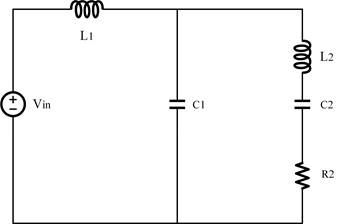
matlab代码：

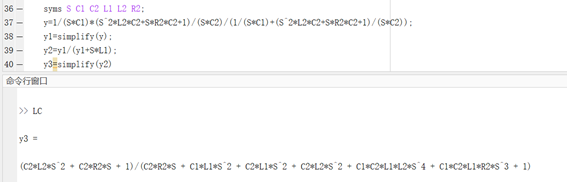
得到的结果如下：

分析其波特图和阶跃响应（阶跃响应时域公式可以通过传递函数和1/s相乘后的拉普拉斯反变换得到）：

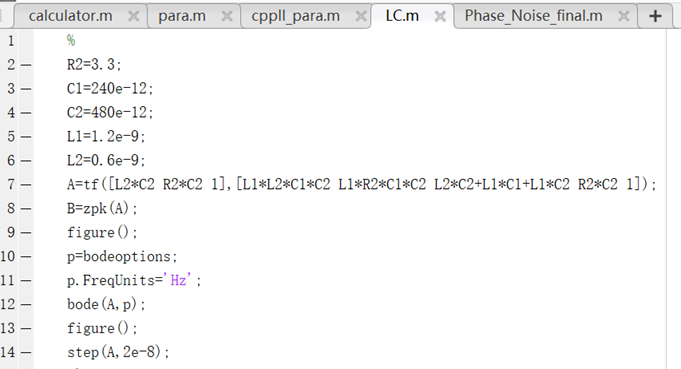
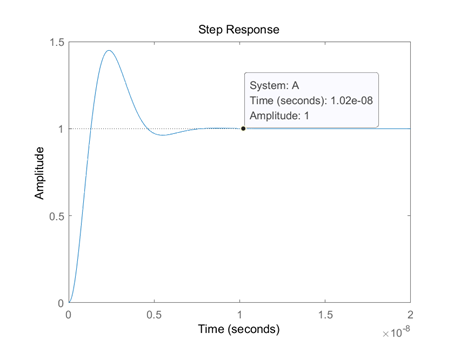
对于多极点系统，二阶系统的分析方法已经不再使用，这时候需要用到根轨迹法，应用根轨迹法分析RLC谐振电源去耦中R2电阻取值对于系统建立的影响；

根据化简为：

代码：（注意因为电容电感值比较小可以能会被忽略，使用tf再用zpk会有更好的效果）

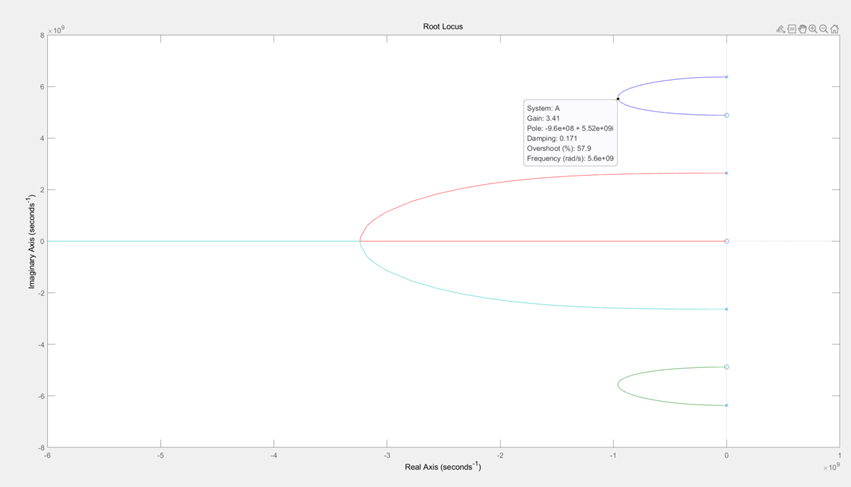
R2从0到无穷大，特征根从开环的极点变成0点，取damping最好的R2值，上下两个虚轴附近的特征根的最优R2大约为3.2-3.4之间，随着R2增大阻尼系数先增大后减小，中间两个特征根最优R2为4.82-无穷大，从0-4.82之间随着R2增大而增大而后保持为1。

分析时域和波特图代码：

（1）R2为3.3时：

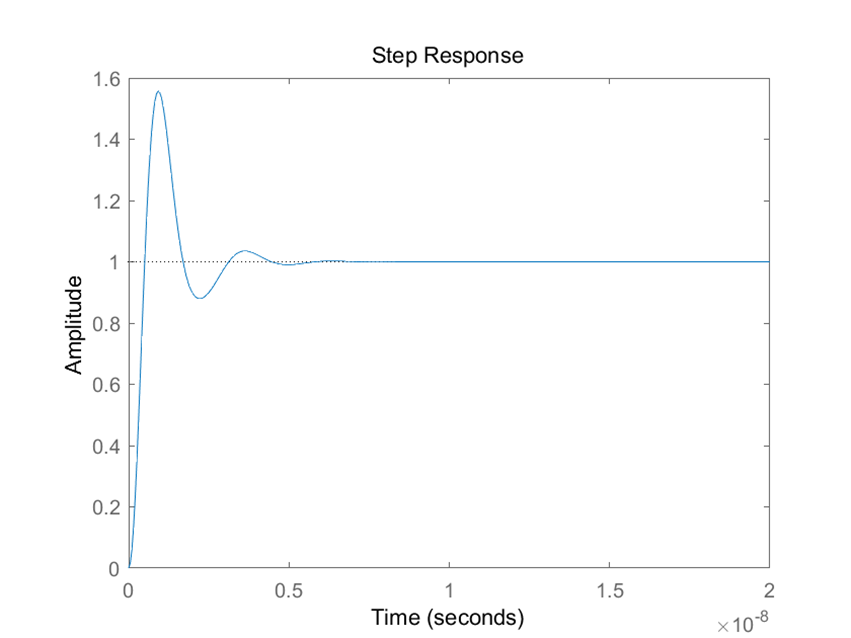
（2）R2为4.82时：

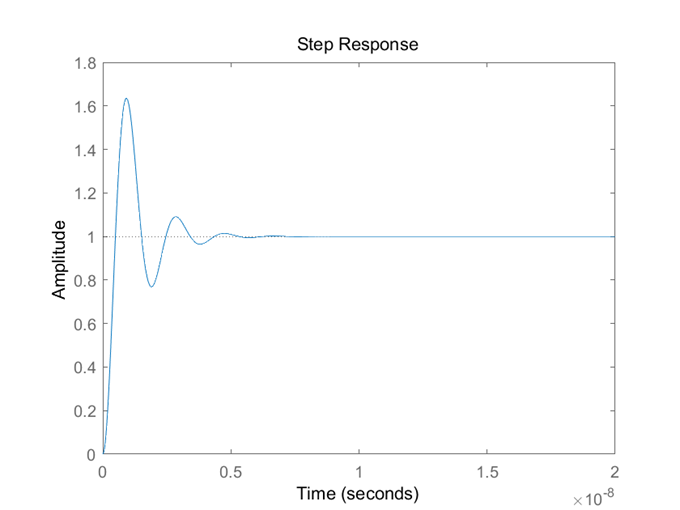
实际上R2在3.2-4.82之间都有相对不错的阶跃响应。

方法二：

根据电路列写节点电流方程，再用符号变量解出方程得到传递函数，比较通用。

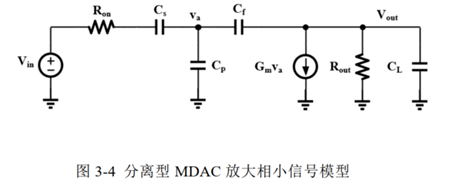
节点va流入电流等于流出电流，假定流入为正：

节点Vout流入电流等于流出电流，假定流出为正：

Matlab代码：

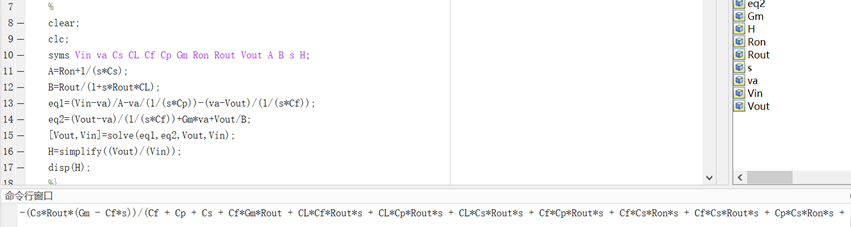
Simplify能够化简符号函数；

方法三：simulink分析非线性系统

Matlab里simulink的Discontinuities模块（间断、不连续）经常用于非线性系统分析

分析MDAC里使用增益自举技术运放的零极点对对系统建立时间的影响

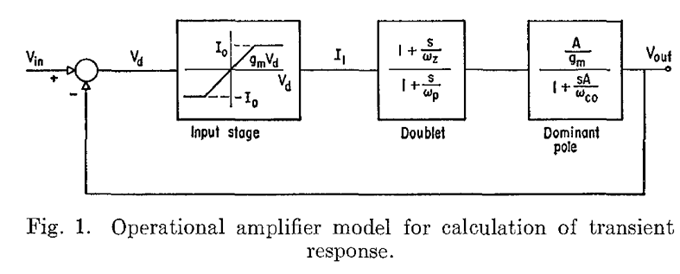
增益设置为90dB，GBW为3GHz，输出最大电流为12mA，跨导gm为20mS，系统波特图，零极点对产生的影响和预期一样，靠得比较近的话基本没有影响。

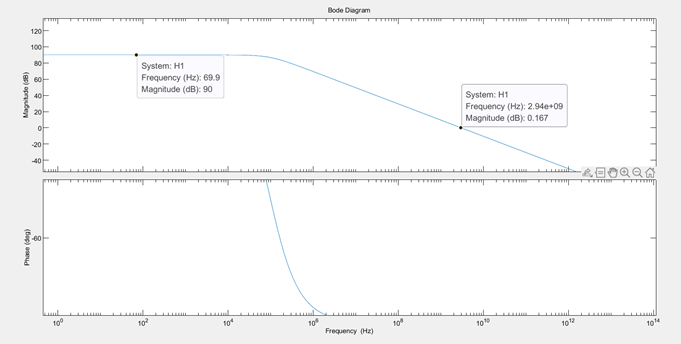
Simulink仿真：

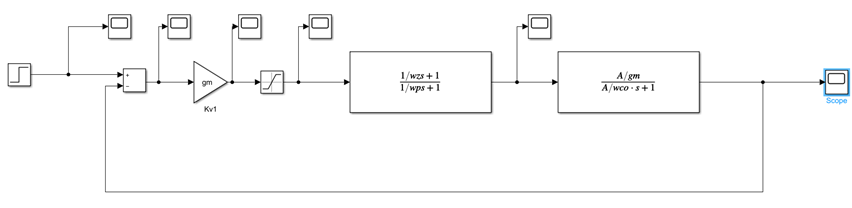
输入阶跃信号从0变化到10，幅度为0.6时系统进入压摆状态，-0.6-0.6为线性状态，仿真时间设置为10ns，阶跃信号在1ns时变化，对应输出幅度和稳态差值为0.01时是建立到0.1%时刻，输出幅度和稳态差值为0.001时是建立到0.01%时刻。（由于精度只能到小数点后三位，所以幅度设置为10，注意这里并非建立时间，实际上要减去阶跃信号未变化时的1ns和多余的压摆时间）

正如论文里的结论：

1、零极点对差值越大，阶跃响应中出现的过冲越大

2、零极点对频率越高，建立到0.01%的时间越快，但是由于0.1%的建立主要受到过冲幅度的影响，所以零极点对频率变化对该建立时间影响不大

3、对于一个14位满量程为1V的ADC，假设首级量化3位，考察其首级MDAC的建立，最差输入从-Vref变化到Vref即幅度变化1V，后续流水级LSB的一半为0.00024414V，即为建立到0.024414%所需的时间，这个时间更接近于0.01%建立；同样是12位的ADC的话，后续流水级LSB的一半为0.00097656V，更接近于0.1%建立，这个时候辅助运放GBW对于建立时间的影响较小，更重要的是减小建立时过冲的幅值，即把零极点对频率差值减小。