快慢指针妙解环形链表

1. 环形链表检测

问题描述：给定链表头节点，判断链表中是否有环。

解决方案：快慢指针法

• 算法思想：

• 慢指针每次移动1步，快指针每次移动2步。
• 若链表有环，快慢指针必会相遇（类似环形跑道上的追及问题）。
• 若快指针抵达链表末尾（None），则无环。

• 数学解释：
  设环周长为 $c$，环入口到相遇点距离为 $d$，头节点到环入口距离为 $k$。
  相遇时慢指针移动距离：$s = k + d$
  快指针移动距离：$2s = k + d + mc$（$m$为整数）
  联立得：$k + d = mc$，即 $k = mc – d$。
  因此，若将慢指针放回头节点，二者同步移动 $k$ 步必在环入口相遇。

代码实现：

def hasCycle(head):
slow = fast = head
while fast and fast.next:
slow = slow.next
fast = fast.next.next
if slow == fast:
return True
return False

2. 两个数组的交集

问题描述：给定两个整数数组，返回它们的交集（元素可重复）。

解决方案：哈希表计数法

• 算法思想：

• 统计 nums1 中每个元素的出现频次。
• 遍历 nums2，若元素在哈希表中且频次 $>0$，则加入结果并减少频次。

• 数学表达：
  设数组 $A$ 长度为 $m$，$B$ 长度为 $n$。
  时间复杂度：$O(m + n)$
  空间复杂度：$O(\\min(m, n))$（哈希表存储较小数组）

代码实现：

def intersect(nums1, nums2):
count = {}
res = []
for num in nums1:
count[num] = count.get(num, 0) + 1
for num in nums2:
if num in count and count[num] > 0:
res.append(num)
count[num] -= 1
return res

3. 随机链表的深拷贝

问题描述：深拷贝一个带随机指针的链表，其中 random 可能指向任意节点或 None。

解决方案：三步拆解法

• 算法思想：

  

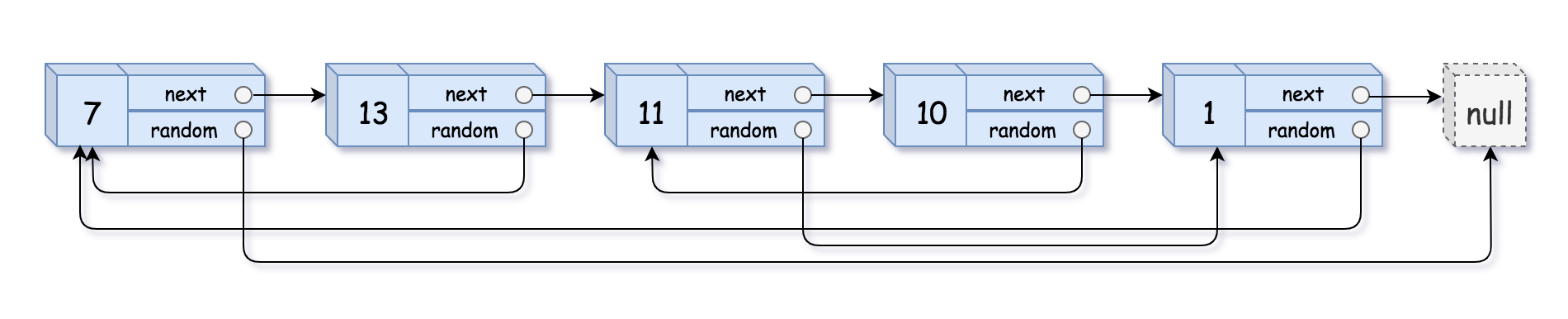
• 创建拷贝节点：在原节点后插入新节点（如 A→A'→B→B'）。
• 连接随机指针：若原节点 cur.random 存在，则 cur.next.random = cur.random.next。
• 分离链表：将新节点分离为独立链表。

代码实现：

def copyRandomList(head):
if not head: return None
# 1. 插入拷贝节点
cur = head
while cur:
new_node = Node(cur.val)
new_node.next = cur.next
cur.next = new_node
cur = new_node.next
# 2. 连接随机指针
cur = head
while cur:
if cur.random:
cur.next.random = cur.random.next
cur = cur.next.next
# 3. 分离链表
cur = head
new_head = head.next
while cur:
copy = cur.next
cur.next = copy.next
if copy.next:
copy.next = copy.next.next
cur = cur.next
return new_head

总结：

• 环形链表：快慢指针的追及模型。
• 数组交集：哈希表统计频次。
• 随机链表：利用节点邻接关系复制指针。
  通过这三个问题，可深入理解指针操作、空间优化和链表结构处理技巧。