自动驾驶轨迹规划算法——Apollo EM Planner

文章目录

自动驾驶轨迹规划算法——Apollo EM Planner
一、Apollo EM Planner 是什么？
- 1.1 定义与核心思想
- 1.2 与其他规划器（如 Lattice、Hybrid A*）的区别
- 1.3 Apollo EM Planner 的典型应用场景
二、Apollo EM Planner 的原理（参考官方架构解析）
- 2.1 规划器总体架构：EM 迭代优化思想
- 2.2 坐标系选择：Frenet 坐标系的优势
- **2.3　E-Step：路径优化阶段**
- - **2.3.1 背景问题**
  - **2.3.2 核心思想**
  - **2.3.3 Step-by-Step 过程**
  - - **Step 1 — SL 投影与可行区域生成**
    - **Step 2 — 动态规划（DP）搜索粗路径**
    - **Step 3 — 生成可行走廊（Feasible Tunnel）**
    - **Step 4 — QP + 样条曲线平滑优化**
  - **2.3.4 数学建模**
  - **2.3.5 可视化示意**
  - **2.3.6 结果意义**
- **2.4 M-Step：速度优化阶段**
- - **2.4.1 背景问题**
  - **2.4.2 核心思想**
  - **2.4.3 Step-by-Step 过程**
  - - **Step 1 — ST 投影与安全区域生成**
    - **Step 2 — 动态规划（DP）搜索速度曲线**
    - **Step 3 — 生成速度走廊（Feasible ST Tunnel）**
    - **Step 4 — QP 平滑速度曲线**
  - **2.4.4 E–M 交互机制**
  - **2.4.5 结果意义**
- **2.5 E-Step 与 M-Step 的交互机制**
- - **2.5.1 概述**
  - **2.5.2 迭代流程**
  - **2.5.3 执行频率**
  - **2.5.4 交互机制的优势**
- 三、Apollo EM Planner 的关键技术细节
- - 3.1 规划问题建模
  - 3.2 E-Step 核心技术（S–L 平面）
  - - 3.2.1 障碍物投影与占据区生成
    - 3.2.2 动态规划粗搜索
    - 3.2.3 二次规划平滑
  - 3.3 M-Step 核心技术（S–T 平面）
  - - 3.3.1 S–T 投影与安全区构建
    - 3.3.2 DP 粗速度曲线搜索
    - 3.3.3 安全走廊（ST Tunnel）生成
    - 3.3.4 QP 平滑速度曲线
  - 3.4 E–M 迭代机制
  - - 3.4.1 交互流程
    - 3.4.2 优势
  - 3.5 模块间数据交互

一、Apollo EM Planner 是什么？

1.1 定义与核心思想

Apollo EM Planner 是百度 Apollo 自动驾驶系统中的一款实时轨迹规划器（Motion Planner），其命名中的“EM”源自 Expectation–Maximization（期望–最大化）迭代优化的思想。它的核心思路是将轨迹规划问题拆解为“路径优化”和“速度优化”两个子问题，并在二者之间反复交替迭代，直到收敛为止。这种方法能够有效降低规划问题的维度与计算复杂度，同时保持较高的轨迹平滑性与实时性。

在自动驾驶系统中，EM Planner 主要负责：

根据车辆当前位置、参考路径和障碍物信息，规划一条安全、平滑且舒适的轨迹；
在路径规划的基础上分配合理的速度曲线；
在动态环境中快速重规划，保证车辆安全行驶。

1.2 与其他规划器（如 Lattice、Hybrid A*）的区别

特性Lattice PlannerHybrid A* PlannerEM Planner

规划空间	离散采样搜索	连续曲线搜索	Frenet 坐标下路径/速度解耦
核心方法	状态采样+轨迹库	A* 搜索+曲率约束	DP（动态规划）+QP（二次规划）迭代
轨迹平滑性	中等	较高	高（样条曲线平滑）
动态障碍物处理	较弱	较弱	强（ST 投影+速度优化）
实时性	一般	较低	高
适用场景	有限复杂度环境	弯曲狭窄空间	城市道路、高速、动态场景

EM Planner 最大的不同点在于将规划问题分为路径与速度两个独立的优化子问题，并在两者之间交替优化，这不仅提升了实时性，还能应对动态障碍物。

1.3 Apollo EM Planner 的典型应用场景

EM Planner 具有较强的通用性和动态环境适应能力，主要应用在以下自动驾驶任务中：

轨迹跟踪与速度规划（Trajectory & Speed Optimization）在参考路径的基础上，规划符合安全、舒适性要求的轨迹与速度曲线，实现精准跟踪。

车道保持与换道策略（Lane Keeping / Lane Changing）处理多车道场景下的车道保持与换道决策，并在换道过程中平滑过渡。

避障与会车处理结合障碍物动态预测信息，在路径与速度优化阶段实现主动避障与安全会车。

城市道路与高速公路混合场景能够在密集交通和高速行驶场景下保持稳定规划性能，适应各种速度和车道条件。

二、Apollo EM Planner 的原理（参考官方架构解析）

Apollo EM Planner 的设计核心是路径–速度解耦 + EM 迭代优化。它将轨迹规划问题分解为两个子问题：

E-Step：固定速度分布，优化路径形状（Path Planning）。
M-Step：固定路径形状，优化速度曲线（Speed Planning）。

这种交替优化方式可以在保持计算效率的同时，兼顾安全性、平滑性和动态障碍物处理能力。

2.1 规划器总体架构：EM 迭代优化思想

输入：高精地图、参考路线、障碍物信息（静态 + 动态）、车辆当前状态。
输出：时空轨迹（x(t), y(t), v(t), a(t), δ(t)）。
核心循环：
将环境与车辆状态投影到 Frenet 坐标系（S-L / S-T 平面）。
在 S-L 平面进行路径优化（E-Step）。
在 S-T 平面进行速度优化（M-Step）。
检查收敛条件，若未收敛则返回 E-Step 继续迭代。

2.2 坐标系选择：Frenet 坐标系的优势

Apollo EM Planner 在 Frenet 坐标系中进行优化：

S（Station）：沿参考线的弧长位置。
L（Lateral）：横向偏移。
T（Time）：时间维度（用于速度优化）。

优势：

可以将二维轨迹问题分解为一维纵向（S）和一维横向（L）优化问题。

障碍物的空间位置和运动预测在 Frenet 坐标中更容易计算时空交集。

约束表达简单（限速、加速度、车道边界等可直接映射为坐标边界）。

2.3　E-Step：路径优化阶段

2.3.1 背景问题

E-Step 的目标是得到一条不碰障碍物且拓扑合理的路径。如果直接用二次规划（QP）进行路径优化，会遇到两个问题：

QP 是局部优化器，不会自动选择换道或绕障的全局拓扑路径；

障碍物可能让可行域不连通，QP 可能陷入局部无解。

因此 Apollo EM Planner 在 QP 之前增加了动态规划（DP）搜索粗路径，先解决“走哪条道”的全局决策，再在它周围进行平滑优化。

2.3.2 核心思想

在 Frenet S–L 平面（纵向弧长
每个纵向采样位置 $s_k sk 上，取若干横向候选点 l k , j l_{k,j} lk,j。$
边：从 $(s_{k-1}, l_{k-1,i}) (sk−1,lk−1,i) 到 ( s k , l k , j ) (s_k, l_{k,j}) (sk,lk,j) 的一条可能路径段。$
代价：每条边都有一个综合代价，结合平滑性、避障、安全、换道等指标。
搜索：用 DP 在这个有向无环图（DAG）上找到总代价最小的路径。

结果是一条折线型的粗路径，能够绕过障碍物，并在全局上代价最优。

2.3.3 Step-by-Step 过程

Step 1 — SL 投影与可行区域生成

将车道边界和障碍物包络（膨胀

\\frac{w}{2} + b 2w​+b）投影到 S–L 平面；

得到每个纵向位置上的可行横向区间：

(

)

[

min

⁡

(

)

max

⁡

(

)

]

∖

(

)

\\mathcal{L}_{\\mathrm{free}}(s) = [l_{\\min}(s), l_{\\max}(s)] \\setminus \\mathrm{Obs}(s)

$L_{free} (s) = [l_{m i n} (s), l_{m a x} (s)] ∖ Obs (s)$

Step 2 — 动态规划（DP）搜索粗路径

Step 2.1 网格构建

纵向采样：

⋅

…

s_k = s_0 + k \\cdot \\Delta s, \\quad k = 0, 1, \\dots, K

$s_{k} = s_{0} + k \cdot Δ s, k = 0, 1, \dots, K$

通常

1
⁣

∼
⁣

\\Delta s = 1\\! \\sim\\! 2\\,\\mathrm{m}

$Δ s = 1 \sim 2 m$ ；

横向采样：在每个 $s_k sk 的可行区间内取若干 l k , j l_{k,j} lk,j（等间距或中心加密）；$
可行性过滤：若 $(s_k, l_{k,j}) (sk,lk,j) 落在障碍物膨胀区内，则直接剔除。$

Step 2.2 建立转移规则

允许的转移需满足：

∣

−

∣

≤

max

⁡

\\left|\\frac{l_{k,j} – l_{k-1,i}}{\\Delta s}\\right| \\le \\sigma_{\\max}

Δslk,j−lk−1,i

≤σmax,

∣

−

∣

≤

max

⁡

\\left|\\frac{l_{k,j} – 2l_{k-1,i} + l_{k-2,h}}{\\Delta s^2}\\right| \\le \\alpha_{\\max}

Δs2lk,j−2lk−1,i+lk−2,h

≤αmax

并且该线段不与障碍物相交；

违反条件的边不建立。

Step 2.3 定义代价函数

C_{\\mathrm{edge}} = w_{\\mathrm{dev}} C_{\\mathrm{dev}} + w_{\\mathrm{cur}} C_{\\mathrm{cur}} + w_{\\mathrm{obs}} C_{\\mathrm{obs}} + w_{\\mathrm{lc}} C_{\\mathrm{lc}}

$C_{edge} = w_{dev} C_{dev} + w_{cur} C_{cur} + w_{obs} C_{obs} + w_{lc} C_{lc}$

偏离代价：

(

−

(

)

C_{\\mathrm{dev}} = (l_{k,j} – l_{\\mathrm{ref}}(s_k))^2

$C_{dev} = (l_{k, j} - l_{ref} (s_{k}))^{2}$

平滑性代价：

(

−

)

C_{\\mathrm{cur}} = \\left(\\frac{l_{k,j} – 2l_{k-1,i} + l_{k-2,h}}{\\Delta s^2}\\right)^2

$C_{cur} = (\frac{l _{k, j} - 2 l _{k - 1, i} + l _{k - 2, h}}{Δ s ^{2}})^{2}$

障碍物距离代价：

(

)

C_{\\mathrm{obs}} = \\phi(\\mathrm{dist}(l_{k,j}, B(s_k)))

$C_{obs} = ϕ (dist (l_{k, j}, B (s_{k})))$

换道惩罚 $C_{\\mathrm{lc}} Clc：跨越车道中心线则加固定代价。$

Step 2.4 动态规划求最优路径

初始化：

(

)

\\mathrm{Cost}(s_0, l_0) = 0

$Cost (s_{0}, l_{0}) = 0$

递推：

(

)

min

⁡

−

∈

feasible

[

(

−

)

]

\\mathrm{Cost}(s_k, l_{k,j}) = \\min_{l_{k-1,i} \\in \\text{feasible}} \\left[ \\mathrm{Cost}(s_{k-1}, l_{k-1,i}) + C_{\\mathrm{edge}} \\right]

$Cost (s_{k}, l_{k, j}) = min_{l_{k - 1, i} \in feasible} [Cost (s_{k - 1}, l_{k - 1, i}) + C_{edge}]$

记录前驱指针，回溯得到粗路径：

(

)

(

)

…

(

)

\\tilde{l}(s_0), \\tilde{l}(s_1), \\dots, \\tilde{l}(s_K)

$\tilde{l} (s_{0}), \tilde{l} (s_{1}), \dots, \tilde{l} (s_{K})$

Step 3 — 生成可行走廊（Feasible Tunnel）

以 DP 粗路径为中心，向左右扩展固定半宽 δ\\deltaδ；

半宽 δ\\deltaδ 计算方法：

δ

E

=

W

veh

2

+

W

obs

2

+

d

safe

\\delta_{\\text{E}} = \\frac{W_{\\text{veh}}}{2} + \\frac{W_{\\text{obs}}}{2} + d_{\\text{safe}}

$δ_{E} = \frac{W _{veh}}{2} + \frac{W _{obs}}{2} + d_{safe}$

其中：
- $W_{\\text{veh}} Wveh：车辆宽度$
- $W_{\\text{obs}} Wobs：障碍物宽度$
- $d_{\\text{safe}} dsafe：额外安全裕度（可根据速度动态调整： δ E ⁣ + = k v ⋅ ∣ v rel ∣ \\delta_{\\text{E}} \\!+= k_v \\cdot |v_{\\text{rel}}| δE+=kv⋅∣vrel∣）$
这样得到的

δ

E

\\delta_{\\text{E}}

$δ_{E}$ 表示障碍物横向占据区的“安全半宽”，确保走廊不会过于贴近障碍物边缘。

与

(

)

\\mathcal{L}_{\\mathrm{free}}(s)

$L_{free} (s)$ 相交，裁剪出安全走廊；

走廊保证不与障碍物重叠，所有轨迹点

(

)

l(s)

$l (s)$ 均需在走廊范围内。

Step 4 — QP + 样条曲线平滑优化

参数化路径：

(

)

(

−

)

(

−

)

(

−

)

l(s) = a_0 + a_1(s – S_i) + a_2(s – S_i)^2 + a_3(s – S_i)^3

$l (s) = a_{0} + a_{1} (s - S_{i}) + a_{2} (s - S_{i})^{2} + a_{3} (s - S_{i})^{3}$

确保段间

C^2

$C^{2}$ 连续。

优化目标：

min

⁡

(

)

∫

(

′

)

\\min_{l(s)} \\int_{s_0}^{s_f} \\left( w_0\\,l^2 + w_1\\,l'^2 + w_2\\,l''^2 \\right) ds

$min_{l (s)} \int_{s_{0}}^{s_{f}} (w_{0} l^{2} + w_{1} l^{'2} + w_{2} l^{''2}) d s$

约束条件：

走廊边界 $l_{\\mathrm{low}}(s) \\le l(s) \\le l_{\\mathrm{up}}(s) llow(s)≤l(s)≤lup(s)$
曲率限制 $|\\kappa(s)| \\le \\kappa_{\\max} ∣κ(s)∣≤κmax；$
起终点边界条件。

2.3.4 数学建模

E-Step 优化问题可形式化为：

min

⁡

(

)

∫

(

′

)

s.t.

(

)

≤

(

)

≤

(

)

∣

(

)

∣

≤

max

⁡

(

)

′

(

)

tan

⁡

\\begin{aligned} \\min_{l(s)}\\quad & \\int_{s_0}^{s_f} \\big( w_0\\,l^2 + w_1\\,l'^2 + w_2\\,l''^2 \\big)\\,ds \\\\ \\text{s.t.}\\quad & l_{\\mathrm{low}}(s) \\le l(s) \\le l_{\\mathrm{up}}(s), \\\\ & |\\kappa(s)| \\le \\kappa_{\\max}, \\\\ & l(s_0)=l_0,\\quad l'(s_0)=\\tan\\psi_0 \\end{aligned}

$l (s) min s.t. \int_{s_{0}}^{s_{f}} (w_{0} l^{2} + w_{1} l^{'2} + w_{2} l^{''2}) d s l_{low} (s) \leq l (s) \leq l_{up} (s), ∣ κ (s) ∣ \leq κ_{m a x}, l (s_{0}) = l_{0}, l^{'} (s_{0}) = tan ψ_{0}$

2.3.5 可视化示意

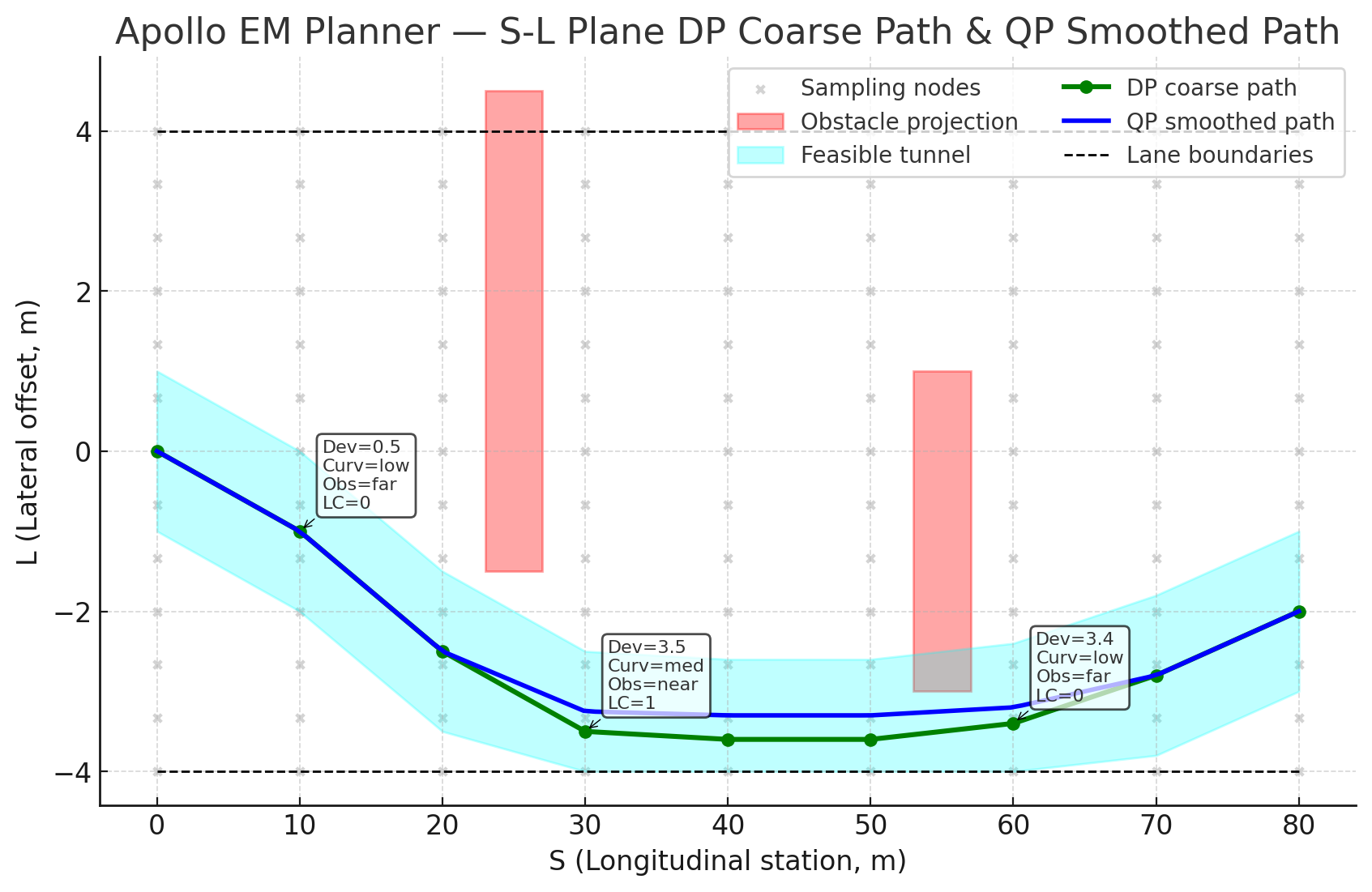
在这里插入图片描述

图例：

灰色点：S–L 平面采样网格
红色矩形：障碍物投影（不可行区）
绿色折线：DP 粗路径（严格避障）
浅蓝带：可行走廊（裁剪后）
蓝色曲线：QP 平滑路径
注释框（Dev / Curv / Obs / LC）：DP 边代价项说明

（这里可插入我们绘制的严格避障图）

2.3.6 结果意义

DP 粗路径：解决全局拓扑选择（绕障、换道），保证无碰撞；
可行走廊：将 QP 优化限制在安全范围内，提高效率与稳定性；
QP 平滑路径：提升舒适性和可控性，并为速度优化提供曲率上界。

2.4 M-Step：速度优化阶段

2.4.1 背景问题

E-Step 已经在 S–L 平面生成了一条平滑、避障、安全的路径形状

(

)

l(s)

$l (s)$ 。 M-Step 的任务是在该路径上分配一个合理的速度曲线

(

)

v(s)

$v (s)$ 或

(

)

v(t)

$v (t)$ ，使车辆在动态环境中既能高效行驶，又能满足安全、舒适和动力学约束。

如果不进行速度优化，常见问题包括：

无法正确处理动态障碍物的交互（让行、超车、跟随等）；
速度变化不平滑，乘坐体验差；
超过车辆动力学极限（加速度、加加速度超标）。

因此，M-Step 会将障碍物与路径结合投影到 S–T 平面，先用动态规划（DP）在时空域选择一条安全的速度曲线，再用二次规划（QP）进行平滑优化。

2.4.2 核心思想

投影

将路径 $(x_{obs}(t), y_{obs}(t)) (xobs(t),yobs(t)) 投影到 S–T 平面（Station–Time）。$
障碍物预测轨迹通过 Frenet 转换得到 $s_{obs}(t) sobs(t) 与 l o b s ( t ) l_{obs}(t) lobs(t)，并结合横向重叠条件生成障碍物禁入区。$

DP 搜索

在 S–T 平面搜索一条从 $(s_0, t_0) (s0,t0) 到 ( s f , t f ) (s_f, t_f) (sf,tf) 的粗略曲线 s ( t ) s(t) s(t)，避开障碍物时空占据区，处理避障与交互策略。$

QP 优化

在 DP 结果的安全走廊内优化速度曲线，确保平滑性与动力学可行性。

输出

生成最终速度–时间曲线

2.4.3 Step-by-Step 过程

Step 1 — ST 投影与安全区域生成

路径映射：将 E-Step 路径

l

(

s

)

l(s)

$l (s)$ 转换为 Frenet 坐标系下的纵向位置

s

s

$s$ 。
障碍物预测：获取感知与预测模块提供的障碍物未来轨迹，并转换到 Frenet 坐标得到

s

o

b

s

(

t

)

s_{obs}(t)

$s_{o b s} (t)$ 区间。
时间引入：
- 初始参考路径假设车辆以期望速度
  
  v
  
  r
  
  e
  
  f
  
  v_{ref}
  
  $v_{re f}$ 行驶，通过
  
  t
  
  (
  
  s
  
  )
  
  =
  
  ∫
  
  s
  
  0
  
  s
  
  1
  
  v
  
  (
  
  s
  
  ′
  
  )
  
  d
  
  s
  
  ′
  
  t(s) = \\int_{s_0}^{s} \\frac{1}{v(s')} \\, ds'
  
  $t (s) = \int_{s_{0}}^{s} \frac{1}{v ( s ^{'} )} d s^{'}$
  
  关联纵向位置与时间。
- 在迭代中，每次 M-Step 都基于 E-Step 更新的路径重新计算该映射。
安全区域：

T

free

(

s

)

=

R

+

∖

O

b

s

S

T

(

s

)

T_{\\text{free}}(s) = R^+ \\setminus Obs_{ST}(s)

$T_{free} (s) = R^{+} ∖ O b s_{ST} (s)$

其中

O

b

s

S

T

(

s

)

Obs_{ST}(s)

$O b s_{ST} (s)$ 为障碍物占据的时间区间集合。

Step 2 — 动态规划（DP）搜索速度曲线

2.1 网格构建

纵向采样：沿路径均匀采样 $s_k sk；$
时间采样：每个 $s_k sk 对应若干可能到达时间 t k , j t_{k,j} tk,j；$
可行性过滤：剔除落在障碍物 ST 区域内的点。

2.2 转移规则

平均速度限制：

0

<

Δ

s

Δ

t

≤

v

max

⁡

(

s

k

)

0 < \\frac{\\Delta s}{\\Delta t} \\le v_{\\max}(s_k)

$0 < \frac{Δ s}{Δ t} \leq v_{m a x} (s_{k})$
加速度限制：

⁡

a

min

⁡

≤

Δ

v

Δ

t

≤

a

max

⁡

⁡a_{\\min} \\le \\frac{\\Delta v}{\\Delta t} \\le a_{\\max}

$a_{m i n} \leq \frac{Δ v}{Δ t} \leq a_{m a x}$
jerk 限制可作为软约束或代价项。

2.3 代价函数

edge

time

acc

jerk

eff

C_{\\text{edge}} = w_{\\text{time}}C_{\\text{time}} + w_{\\text{acc}}C_{\\text{acc}} + w_{\\text{jerk}}C_{\\text{jerk}} + w_{\\text{eff}}C_{\\text{eff}}

$C_{edge} = w_{time} C_{time} + w_{acc} C_{acc} + w_{jerk} C_{jerk} + w_{eff} C_{eff}$

$C_{\\text{time}} Ctime：总行驶时间$
$C_{\\text{acc}} Cacc：加速度平方和$
$C_{\\text{jerk}} Cjerk：jerk 平方和$
$C_{\\text{eff}} Ceff：效率惩罚（与期望速度偏差）$

2.4 求解与回溯

初始化：

C

o

s

t

(

s

0

,

t

0

)

=

0

Cost(s_0, t_0) = 0

$C os t (s_{0}, t_{0}) = 0$
递推：

C

o

s

t

(

s

k

,

t

k

,

j

)

=

min

⁡

t

k

−

1

,

i

∈

f

e

a

s

i

b

l

e

[

C

o

s

t

(

s

k

−

1

,

t

k

−

1

,

i

)

+

C

edge

]

Cost(s_k, t_{k,j}) = \\min_{t_{k-1,i} \\in feasible} \\left[ Cost(s_{k-1}, t_{k-1,i}) + C_{\\text{edge}} \\right]

$C os t (s_{k}, t_{k, j}) = min_{t_{k - 1, i} \in f e a s ib l e} [C os t (s_{k - 1}, t_{k - 1, i}) + C_{edge}]$
回溯得到粗时间–位置曲线

t

~

(

s

)

\\tilde{t}(s)

$\tilde{t} (s)$ 。

Step 3 — 生成速度走廊（Feasible ST Tunnel）

以 DP 粗曲线为中心，给每个

s

k

s_k

$s_{k}$ 分配时间区间上下界，避开障碍物 ST 占据区；
时间区间上下界确定方法：
初始区间：根据 DP 粗曲线的时间

t

~

(

s

k

)

\\tilde{t}(s_k)

$\tilde{t} (s_{k})$ ，在其上下扩展固定时间裕度

δ

t

\\delta_t

$δ_{t}$ ：

t

low

(

s

k

)

=

t

~

(

s

k

)

−

δ

t

,

t

up

(

s

k

)

=

t

~

(

s

k

)

+

δ

t

t_{\\text{low}}(s_k) = \\tilde{t}(s_k) – \\delta_t,\\quad t_{\\text{up}}(s_k) = \\tilde{t}(s_k) + \\delta_t

$t_{low} (s_{k}) = \tilde{t} (s_{k}) - δ_{t}, t_{up} (s_{k}) = \tilde{t} (s_{k}) + δ_{t}$

其中

δ

t

\\delta_t

$δ_{t}$ 可根据速度、加速度约束动态调整，例如：

δ

t

=

t

base

+

k

a

⋅

∣

a

max

∣

\\delta_t = t_{\\text{base}} + k_a \\cdot |a_{\\text{max}}|

$δ_{t} = t_{base} + k_{a} \cdot ∣ a_{max} ∣$ 。
安全裁剪：与障碍物 ST 占据区

O

b

s

S

T

(

s

k

)

Obs_{ST}(s_k)

$O b s_{ST} (s_{k})$ 做差集运算：

[

t

low

,

t

up

]

←

[

t

low

,

t

up

]

∖

O

b

s

S

T

(

s

k

)

[t_{\\text{low}},\\ t_{\\text{up}}] \\gets [t_{\\text{low}},\\ t_{\\text{up}}] \\setminus Obs_{ST}(s_k)

$[t_{low}, t_{up}] \leftarrow [t_{low}, t_{up}] ∖ O b s_{ST} (s_{k})$

确保时间走廊不与障碍物重叠。
可行性检查：如果裁剪后区间为空，则需回退到 E-Step 重新规划路径。
最终得到的

{

[

t

low

(

s

k

)

,

t

up

(

s

k

)

]

}

\\{[t_{\\text{low}}(s_k),\\ t_{\\text{up}}(s_k)]\\}

${[t_{low} (s_{k}), t_{up} (s_{k})]}$ 组成 Feasible ST Tunnel，供 QP 优化阶段使用。

Step 4 — QP 平滑速度曲线

优化变量：

s

(

t

)

s(t)

$s (t)$ 或

v

(

t

)

v(t)

$v (t)$ ；
目标函数：

min

⁡

∑

i

[

w

a

a

i

2

+

w

j

j

i

2

+

w

v

(

v

i

−

v

des

)

2

]

\\min \\sum_i \\left[ w_a a_i^2 + w_j j_i^2 + w_v (v_i – v_{\\text{des}})^2 \\right]

$min \sum_{i} [w_{a} a_{i}^{2} + w_{j} j_{i}^{2} + w_{v} (v_{i} - v_{des})^{2}]$
约束条件：
- ST 走廊约束
- $\\le v_i \\le v_{\\max}(s_i) 0≤vi≤vmax(si)$
- $a_{\\min} \\le a_i \\le a_{\\max} amin≤ai≤amax$
- jerk 限制
- 起点/终点速度条件

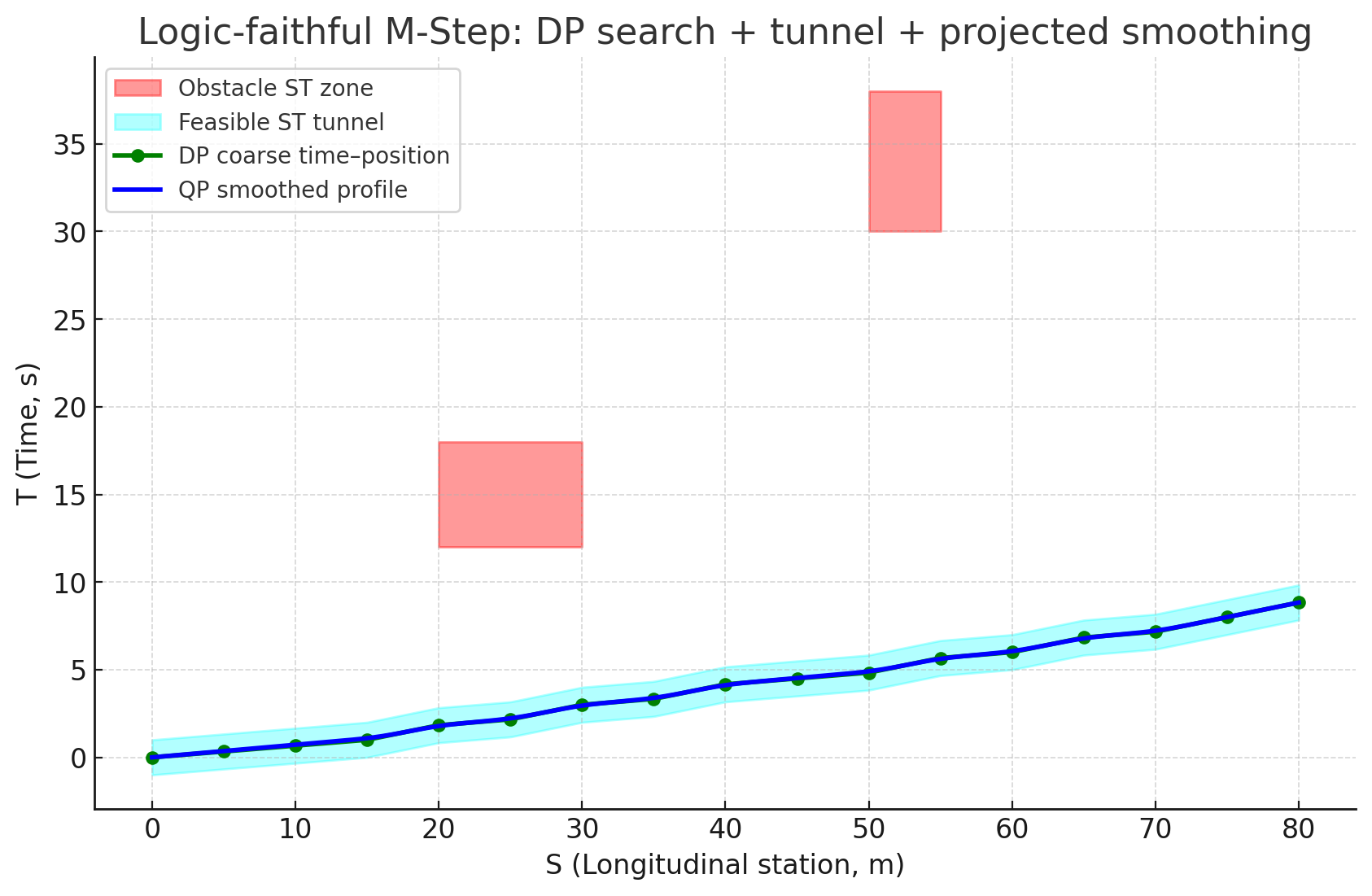
在这里插入图片描述

2.4.4 E–M 交互机制

M-Step 检查当前路径与障碍物的时空冲突：
- 无冲突 → 直接优化速度曲线；
- 有冲突 → 返回 E-Step 重新优化路径（可能换道或横向调整）。
每次迭代都会基于最新的路径重新计算 ST 投影和速度曲线，从而逐步逼近同时满足空间与时间可行性的解。

2.4.5 结果意义

DP 曲线：提供全局时序策略（让行、跟随、超车）。
速度走廊：限制 QP 优化在安全范围内，提高计算效率。
QP 曲线：保证平滑、舒适和动力学可行性。
合成时空轨迹：

2.5 E-Step 与 M-Step 的交互机制

2.5.1 概述

在 Apollo EM Planner 中，E-Step（S–L 空间的路径规划）与 M-Step（S–T 空间的速度规划）通过紧密迭代循环协作，确保最终生成的轨迹既不碰撞又动力学可行。交互的必要性在于：

E-Step 解决空间可行性与拓扑选择（保持车道、换道、避静态障碍物）。
M-Step 解决时间可行性（避动态障碍物、保证加减速舒适）。
一条空间上可行的路径，在时间域上可能依然不可行（例如前方有移动障碍物阻挡）。

2.5.2 迭代流程

初始路径生成（E-Step）

基于路由和地图模块提供的参考线。
在 S–L 平面执行动态规划（DP）粗搜索 + 二次规划（QP）平滑，得到一条无静态障碍物碰撞且曲率平滑的横向轨迹 l(s)l(s)l(s)。
输出路径解决了 “走哪条道、绕哪边障” 的全局空间决策问题。

投影到时间域（M-Step 输入）

将 E-Step 轨迹
将动态障碍物的预测轨迹 $(x_{obs}(t), y_{obs}(t)) (xobs(t),yobs(t)) 转换到 Frenet 坐标系 ( s o b s ( t ) , l o b s ( t ) ) (s_{obs}(t), l_{obs}(t)) (sobs(t),lobs(t))。$
得到 S–T 平面的障碍物禁入区（Obstacle Forbidden Zone）。

S–T 碰撞检测

检查车辆沿路径的纵向位置
s

(

t

)

s(t)

$s (t)$ 是否与障碍物禁入区重叠：
- 发生重叠 → 反馈回 E-Step 重新规划空间路径（如提前换道或调整横向偏移）。
- 未重叠 → 进入速度优化阶段。

速度优化（M-Step）

在可行的时空走廊内先用 DP 粗规划

生成最终轨迹

将 E-Step 的

2.5.3 执行频率

整个 E–M 循环以滚动规划（rolling planning）方式运行，通常每 100 ms 执行一次。
每一轮都会更新：
- 当前车辆状态作为新的起点。
- 最新的地图与障碍物信息。
即使 HD Map 提供的参考线不变，E-Step 输出的路径也可能因交通状况和障碍物变化而微调。

2.5.4 交互机制的优势

全局–局部协同：E-Step 决定可行走廊的拓扑，M-Step 在该走廊内优化行驶时序。
动态避障能力强：若时间域不可行，可提前触发空间重规划。
鲁棒性高：每周期持续评估环境变化，快速适应动态场景。

三、Apollo EM Planner 的关键技术细节

3.1 规划问题建模

Apollo 的 EM Planner 将轨迹规划问题分解为路径与速度两个子问题，通过交替优化求解。

路径优化（E-Step）：在 S–L 平面生成安全、平滑、可行的横向轨迹
速度优化（M-Step）：在固定路径上，于 S–T 平面生成满足避障、动力学与舒适性要求的速度曲线

整体优化目标可抽象为：

min

⁡

(

)

lat

smooth

time

acc

jerk

(

)

\\min_{\\mathcal{X}(t)} \\; w_l C_{\\text{lat}} + w_s C_{\\text{smooth}} + w_t C_{\\text{time}} + w_a C_{\\text{acc}} + w_j C_{\\text{jerk}}X(t)

$min_{X (t)} w_{l} C_{lat} + w_{s} C_{smooth} + w_{t} C_{time} + w_{a} C_{acc} + w_{j} C_{jerk} X (t)$

其中：

$C_{\\text{lat}} Clat：横向安全与碰撞惩罚$
$C_{\\text{smooth}} Csmooth：路径曲率与连续性惩罚$
$C_{\\text{time}} Ctime：总行驶时间$
$C_{\\text{acc}} Cacc：加速度平滑性$
$C_{\\text{jerk}} Cjerk：加加速度平滑性$

3.2 E-Step 核心技术（S–L 平面）

3.2.1 障碍物投影与占据区生成

将障碍物的笛卡尔坐标预测轨迹

(x_{\\text{obs}}(t),y_{\\text{obs}}(t)) (xobs​(t),yobs​(t)) 转换为 Frenet 坐标 ( s obs ( t ) , l obs ( t ) ) (s_{\\text{obs}}(t),l_{\\text{obs}}(t)) (sobs​(t),lobs​(t))。

在 S–L 平面上生成障碍物占据多边形区域，并考虑安全裕度

\\Delta l_{\\text{safe}} Δlsafe​。

3.2.2 动态规划粗搜索

网格化 S–L 空间，采样路径点 $(s_k,l_k) (sk,lk)。$
剔除落在障碍物占据区的网格点。
使用 DP 搜索连接起点到终点的最小代价路径（代价包含横向偏移、曲率变化等）。

3.2.3 二次规划平滑

在 DP 粗路径的“可行带”内，用二次规划优化：

min

⁡

(

)

∫

(

)

(

)

−

ref

)

\\min_{l(s)} \\int \\left( w_\\kappa \\kappa(s)^2 + w_l (l(s)-l_{\\text{ref}})^2 \\right) ds

$min_{l (s)} \int (w_{κ} κ (s)^{2} + w_{l} (l (s) - l_{ref})^{2}) d s$

约束条件：
- 横向偏移限制
- 最大曲率限制
- 起点/终点姿态约束

3.3 M-Step 核心技术（S–T 平面）

3.3.1 S–T 投影与安全区构建

将路径

将障碍物预测轨迹投影到

安全区定义：

free

(

)

∖

(

)

T_{\\text{free}}(s) = \\mathbb{R}^+ \\setminus Obs_{\\text{ST}}(s)

$T_{free} (s) = R^{+} ∖ O b s_{ST} (s)$

3.3.2 DP 粗速度曲线搜索

构建 S–T 网格：纵向采样 $s_k sk，时间采样 t k , j t_{k,j} tk,j；$
过滤掉障碍物禁入区网格点；
代价函数：

edge

time

acc

jerk

eff

C_{\\text{edge}} = w_{\\text{time}} C_{\\text{time}} + w_{\\text{acc}} C_{\\text{acc}} + w_{\\text{jerk}} C_{\\text{jerk}} + w_{\\text{eff}} C_{\\text{eff}}

$C_{edge} = w_{time} C_{time} + w_{acc} C_{acc} + w_{jerk} C_{jerk} + w_{eff} C_{eff}$

回溯得到粗时间–位置曲线 t_{(s)\\tilde{t}(s)t}(s)。

3.3.3 安全走廊（ST Tunnel）生成

以粗解为中心，给每个 $s_k sk 分配可行的时间区间 [ t l o w , t u p ] [tlow,tup] [tlow,tup]。$
保证这些时间段不与障碍物禁入区重叠。

3.3.4 QP 平滑速度曲线

优化变量：速度向量 $\\mathbf{v} = [v_1, v_2, \\dots, v_N] v=[v1,v2,…,vN]。$
目标：

min

⁡

∑

(

−

des

)

\\min \\sum_i \\left( w_a a_i^2 + w_j j_i^2 + w_v (v_i – v_{\\text{des}})^2 \\right)

$min \sum_{i} (w_{a} a_{i}^{2} + w_{j} j_{i}^{2} + w_{v} (v_{i} - v_{des})^{2})$

约束：
- 走廊约束：在允许的时间区间通过对应的 sks_ksk；
- 速度、加速度、jerk 边界约束；
- 起点/终点速度条件。

3.4 E–M 迭代机制

3.4.1 交互流程

E-Step → M-Step：

E-Step 生成的新路径作为 M-Step 的基础，M-Step 在该路径上进行速度优化。

M-Step → E-Step：

若 M-Step 得到的速度曲线在回投影后与障碍物发生冲突，则反馈给 E-Step 重新优化路径。

终止条件：

达到最大迭代次数；
路径和速度变化量均低于阈值。

3.4.2 优势

分治优化：减少联合优化的计算复杂度；
可并行扩展：路径与速度可由不同线程处理，提高实时性；
动态适应：可快速响应突发障碍物或交互策略变化。

3.5 模块间数据交互

模块输入数据输出数据说明

E-Step	参考线、障碍物预测、上周期路径	S–L 路径	保证横向安全与平滑
M-Step	S–L 路径、障碍物预测、初始速度	S–T 速度曲线	保证纵向安全与平滑
控制模块	时空轨迹	控制指令	执行车辆加速、制动、转向