PCA降维提升模型训练效率

一.PCA方法降维介绍

二.PCA与随机森林的区别

三.PCA降维的核心思想

1.基（基向量）与坐标系变换

2.方差

3.PCA目标

四.PCA的优缺点

1.优点

2.缺点

五.PCA代码实现与核心参数

1.PCA导入

2.核心参数

六.案例实现

1.读取数据

2.划分数据

3.划分训练数据和测试数据

4.考虑到正反样本数量不均衡，使用过采样方法使数据均衡

5.构建逻辑回归模型完成训练

6.预测测试集并打印数据没有经过降维处理的报告

7.对特征数据集进行PCA降维

8.重复上述操作进行数据的划分，训练和预测

9.完整代码

一.PCA方法降维介绍

1.PCA又叫主成分分析法，是一种降维技术，用于将高维数据压缩到低维数据

2.与随机森林的特征重要性排名不同，PCA不会直接丢弃不重要特征，而是通过数学变换实现数据压缩

二.PCA与随机森林的区别

随机森林通过特征重要性排名辅助特征选择，目的是优化特征集（如替换低效特征）
PCA适用于特征已固定但维度过高的情况，通过数据压缩提升模型训练效率

三.PCA降维的核心思想

1.基（基向量）与坐标系变换

基是描述向量空间的基础工具，通过坐标系（如X轴、Y轴的单位向量）定义点的位置。
坐标系变换（基变化）会改变点的坐标表示。原坐标系下的点在新坐标系（中坐标需重新计算，点的坐标值通过投影到新基向量计算
新坐标系的单位方向向量需归一化（如原方向向量(1,1)的单位长度为√2，归一化为(√2/2, √2/2)）。

2.方差

方差衡量数据分散程度，PCA通过最大化投影后数据的方差确定最优基。

3.PCA目标

PCA目标是将高维数据投影到低维空间（如二维→一维），保留最大原始信息。关键是通过方差最大化选择最优投影方向（基）。

四.PCA的优缺点

1.优点

计算简单，易于实现。
减少特征筛选工作量
保留大部分有效信息，适合高维数据压缩。

2.缺点

降维后特征失去原始含义（不可解释性）。
要求输入数据为连续变量。
可能丢弃贡献率低但重要的成分。

五.PCA代码实现与核心参数

1.PCA导入

使用 sklearn.decomposition.PCA

from sklearn.decomposition import PCA

2.核心参数

源码如下:

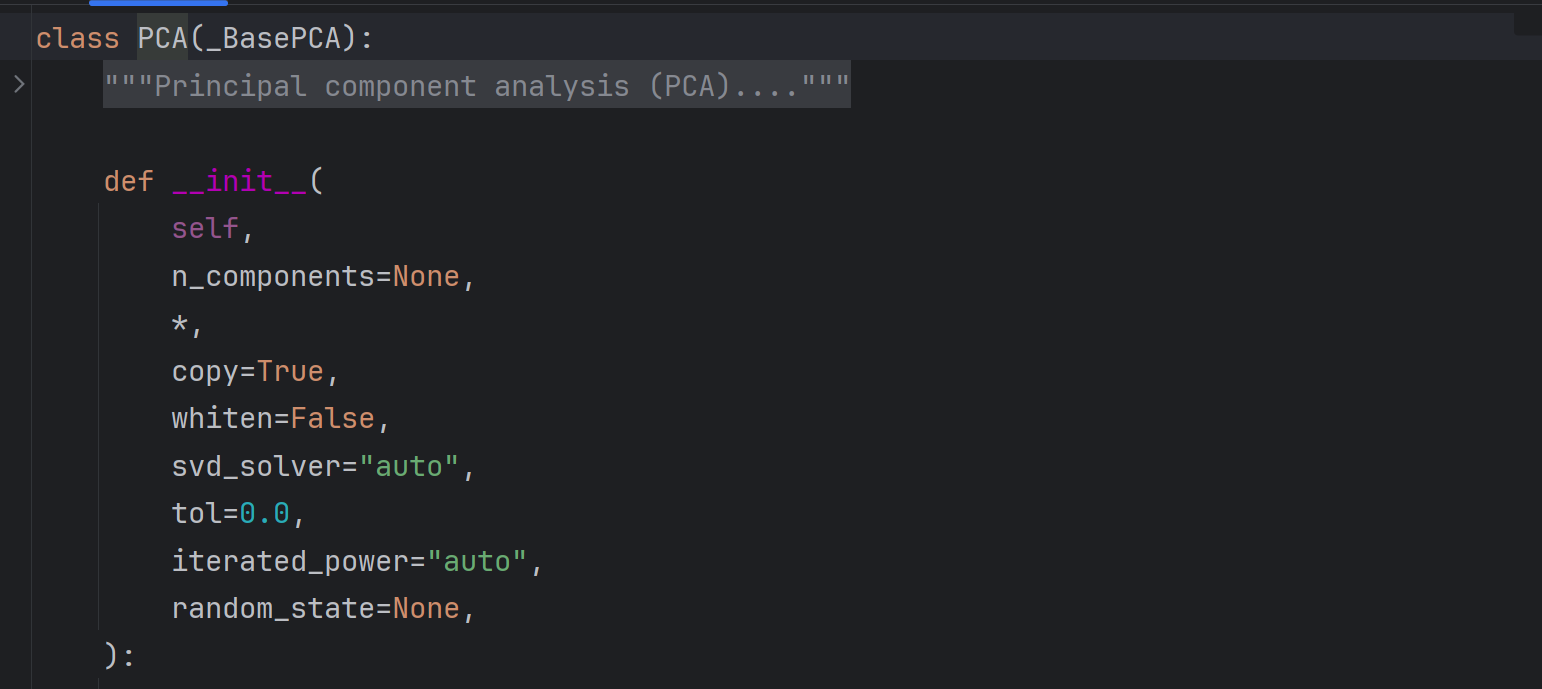
核心参数为n_components即目标维度

六.案例实现

现在有creditcard.csv文件存放银行贷款用户的信息，文件共有31列，第一列是贷款时间，最后一列是类别1表示没有贷款资格，0表示具有贷款资格，需要注意Amount列的数据没有做标准化

1.读取数据

文件有列名，用pandas读取文件，并对Amount列的数据做标准化处理

import pandas as pd
data=pd.read_csv('creditcard.csv')
# 数据标准化
from sklearn.preprocessing import StandardScaler
scaler=StandardScaler()
data['Amount']=scaler.fit_transform(data[['Amount']])

删除无关列time

data=data.drop(['Time'],axis=1)

2.划分数据

划分特征和分类结果

X=data.iloc[:,:-1]
y=data.iloc[:,-1]

3.划分训练数据和测试数据

先不对数据进行pca降维处理，先看不处理的效果

from sklearn.model_selection import train_test_split
train_x,test_x,train_y,test_y=train_test_split(X,y,test_size=0.3,random_state=100)

4.考虑到正反样本数量不均衡，使用过采样方法使数据均衡

from imblearn.over_sampling import SMOTE
oversample=SMOTE(random_state=0)#保证数据拟合效果，随机种子
os_x_train,os_y_train=oversample.fit_resample(train_x,train_y)

5.构建逻辑回归模型完成训练

lr=LogisticRegression()
lr.fit(os_x_train,os_y_train)

6.预测测试集并打印数据没有经过降维处理的报告

predicted=lr.predict(test_x)
print('========没有pca处理后报告==========')
print(metrics.classification_report(test_y,predicted))

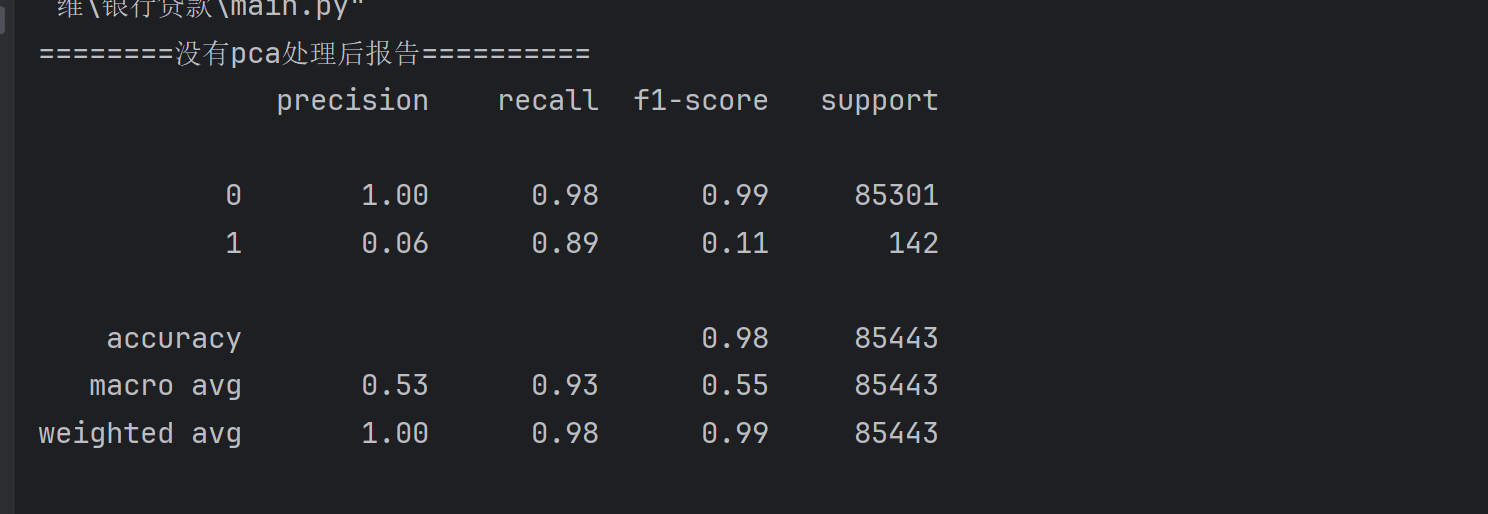
7.对特征数据集进行PCA降维

设置n_comonent=18

使用fit_transform()方法将原来的29维降维成18维数据

pca=PCA(n_components=18)
X_pca=pca.fit_transform(X)

8.重复上述操作进行数据的划分，训练和预测

train_x1,test_x1,train_y1,test_y1=train_test_split(X_pca,y,test_size=0.3,random_state=100)

# 过采样操作
from imblearn.over_sampling import SMOTE
oversample=SMOTE(random_state=0)#保证数据拟合效果，随机种子
os_x_train,os_y_train=oversample.fit_resample(train_x1,train_y1)
lr1=LogisticRegression()
lr1.fit(os_x_train,os_y_train)
predicted=lr1.predict(test_x1)
print('========pca处理后报告==========')
print(metrics.classification_report(test_y1,predicted))

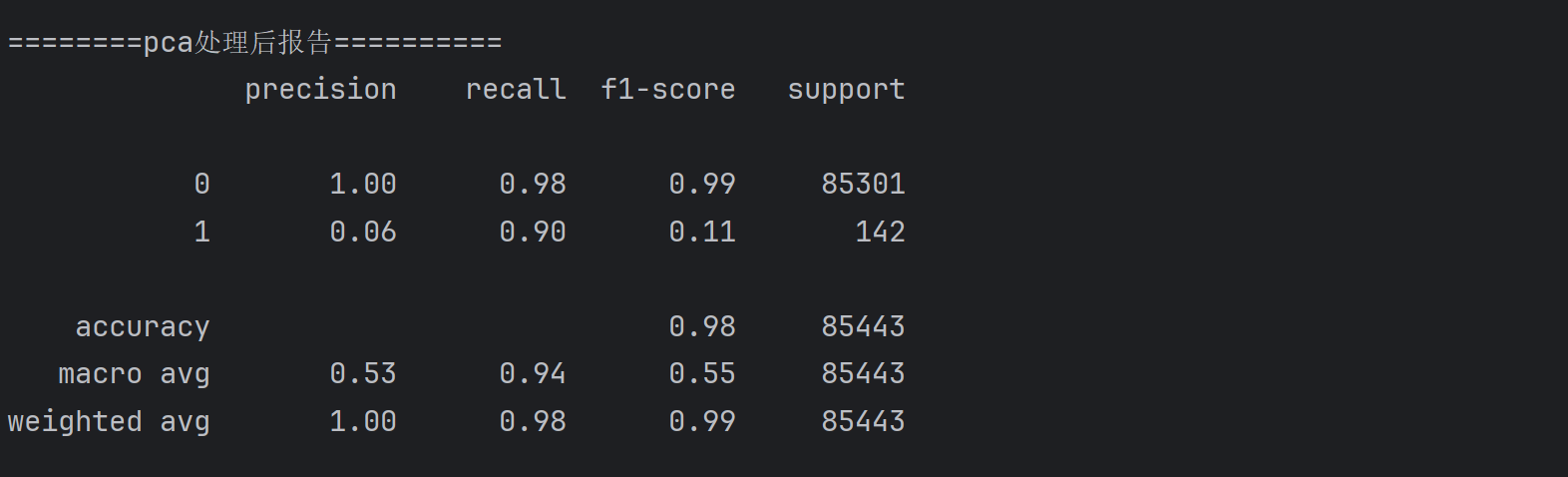
9.完整代码

from sklearn.decomposition import PCA
from sklearn.model_selection import train_test_split
import pandas as pd
from sklearn.linear_model import LogisticRegression
from sklearn import metrics
data=pd.read_csv('creditcard.csv')
# 数据标准化
from sklearn.preprocessing import StandardScaler
scaler=StandardScaler()
data['Amount']=scaler.fit_transform(data[['Amount']])
data=data.drop(['Time'],axis=1)
X=data.iloc[:,:-1]
y=data.iloc[:,-1]
# 不降维
train_x,test_x,train_y,test_y=train_test_split(X,y,test_size=0.3,random_state=100)
from imblearn.over_sampling import SMOTE
oversample=SMOTE(random_state=0)#保证数据拟合效果，随机种子
os_x_train,os_y_train=oversample.fit_resample(train_x,train_y)
lr=LogisticRegression()
lr.fit(os_x_train,os_y_train)
predicted=lr.predict(test_x)
print('========没有pca处理后报告==========')
print(metrics.classification_report(test_y,predicted))
#pca降维
pca=PCA(n_components=18)
X_pca=pca.fit_transform(X)

train_x1,test_x1,train_y1,test_y1=train_test_split(X_pca,y,test_size=0.3,random_state=100)

一.PCA方法降维介绍

二.PCA与随机森林的区别