打卡信奥刷题（1857）用C++实现信奥 P9460 「EZEC-14」众数 I

P9460 「EZEC-14」众数 I

题目背景

pigstd 是一个可爱的男孩子。他在 NOI2022 中的众数一题定义了 $10^6$ 个 std::deque 并没有 MLE。

题目描述

给定一个长度为 $n$ 的序列 $a$，我们通过以下方式构造序列 $b$：

• 初始时 $b=a$。
• 依次对 $b$ 进行 $k$ 次操作，每次操作选择任意一个元素并将其修改为任意整数。

dXqwq 定义一个序列的众数为所有出现次数最大的数。例如 $[1,1,4,5,1,4]$ 的众数为 $1$，而 $[1,14,5,14,19,19,8,10]$ 的众数为 $14,19$。

你需要求出有多少整数可能成为 $b$ 的众数。

输入格式

第一行输入两个整数 $n,k$。

第二行输入 $n$ 个整数 $a_i$。

输出格式

输出一个整数，代表可能成为众数的数的数量。

特别地，如果答案为正无穷，输出 pigstd。

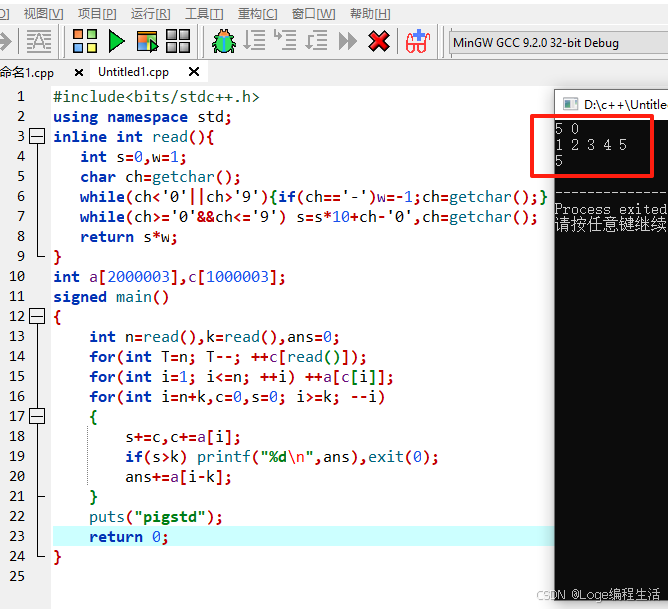
输入输出样例 #1

输入 #1

5 0
1 2 3 4 5

输出 #1

5

输入输出样例 #2

输入 #2

5 1
1 2 3 4 5

输出 #2

pigstd

输入输出样例 #3

输入 #3

5 1
1 1 2 2 3

输出 #3

3

说明/提示

【样例解释】

对于第一组数据，最终 $1,2,3,4,5$ 可能为区间众数。

对于第二组数据，将第一个数换成 $6,7,8,9,\cdots$ 后它们均会成为区间众数，因此答案为正无穷。

对于第三组数据，$1,2,3$ 可能成为区间众数。

【提示】

开 $10^6$ 个 std::deque 在空间限制为 1024MB 时不一定会 MLE。

【数据范围】

本题采用捆绑测试。

• Subtask 1（20 pts）：$n\le 5$。
• Subtask 2（20 pts）：$n\le 10^3$。
• Subtask 3（20 pts）：$k=0$。
• Subtask 4（20 pts）：$k=1$。
• Subtask 5（20 pts）：无特殊限制。

对于 $100\%$ 的数据，$1\le n\le 10^6$，$0\\leq k\\leq n $，$1\le a_i\le n$。

C++实现

#include<bits/stdc++.h>
using namespace std;
inline int read(){
int s=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=–1;ch=getchar();}
while(ch>='0'&&ch<='9') s=s*10+ch–'0',ch=getchar();
return s*w;
}
int a[2000003],c[1000003];
signed main()
{
int n=read(),k=read(),ans=0;
for(int T=n; T—; ++c[read()]);
for(int i=1; i<=n; ++i) ++a[c[i]];
for(int i=n+k,c=0,s=0; i>=k; —i)
{
s+=c,c+=a[i];
if(s>k) printf("%d\\n",ans),exit(0);
ans+=a[i–k];
}
puts("pigstd");
return 0;
}

后续

接下来我会不断用C++来实现信奥比赛中的算法题、GESP考级编程题实现、白名单赛事考题实现，记录日常的编程生活、比赛心得，感兴趣的请关注，我后续将继续分享相关内容