Softmax回归是一种广泛使用的多类分类算法,适用于将输入数据映射到多个离散类别。它是逻辑回归的扩展,常用于图像识别、自然语言处理等领域。其核心是通过softmax函数将线性模型的输出转换为概率分布,从而预测每个类别的可能性。
1. 简介与目的
Softmax回归的目标是解决多类分类问题(例如,将图像分为“猫”、“狗”或“鸟”)。给定输入特征向量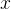 ,模型输出一个概率向量
,模型输出一个概率向量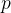 ,其中每个元素
,其中每个元素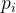 表示输入属于第
表示输入属于第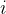 个类别的概率。
个类别的概率。
概率总和为1,即 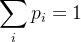 。这使得模型能直观地表示分类不确定性。
。这使得模型能直观地表示分类不确定性。
2. 数学基础
Softmax回归的核心是softmax函数和交叉熵损失函数。
-
Softmax函数:该函数将线性模型的原始输出(称为logits)转换为概率。假设有
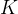 个类别,对于输入
个类别,对于输入 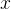 ,模型首先计算logits向量
,模型首先计算logits向量 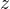 :
: 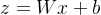 其中:
其中: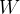 是权重矩阵(维度为
是权重矩阵(维度为 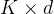 ,
,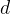 是特征维度),
是特征维度),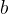 是偏置向量(维度为
是偏置向量(维度为 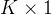 )。 然后,softmax函数将
)。 然后,softmax函数将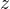 转换为概率
转换为概率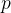 :
: 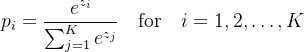 这里,
这里,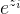 是指数函数,确保输出为正数,且分母归一化使概率和为1。
是指数函数,确保输出为正数,且分母归一化使概率和为1。
-
损失函数:使用交叉熵损失来衡量预测概率
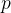 与真实标签
与真实标签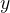 (one-hot编码)的差异。损失函数定义为:
(one-hot编码)的差异。损失函数定义为: 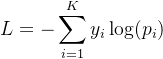 其中
其中 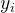 是真实标签的第
是真实标签的第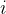 个元素(如果类别正确则为1,否则为0)。最小化该损失可优化模型参数。
个元素(如果类别正确则为1,否则为0)。最小化该损失可优化模型参数。
3. 训练过程
训练Softmax回归涉及优化参数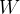 和
和 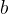 以最小化损失函数
以最小化损失函数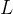 。常用方法是梯度下降:
。常用方法是梯度下降:
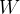 和
和 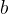 。
。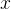 计算
计算 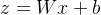 ,然后应用softmax得到
,然后应用softmax得到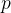 。
。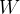 的梯度为:
的梯度为:  其中
其中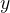 是真实标签。
是真实标签。 ,其中
,其中  是学习率。
是学习率。训练后,模型能预测新样本的类别:选择概率最高的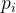 对应的类别。
对应的类别。
4. 应用场景
Softmax回归简单高效,常用于:
- 图像分类(如MNIST手写数字识别)。
- 文本分类(如情感分析)。
- 作为神经网络输出层(例如,在卷积神经网络后接softmax层)。
5. 代码示例
以下是一个简单的Python实现,使用NumPy库进行数值计算。代码包括模型定义、训练和预测功能。
import numpy as np
class SoftmaxRegression:
def __init__(self, num_classes, input_dim, learning_rate=0.01, max_iter=1000):
self.num_classes = num_classes
self.input_dim = input_dim
self.learning_rate = learning_rate
self.max_iter = max_iter
self.W = np.random.randn(num_classes, input_dim) * 0.01 # 初始化权重
self.b = np.zeros((num_classes, 1)) # 初始化偏置
def softmax(self, z):
# 计算softmax概率
exp_z = np.exp(z – np.max(z, axis=0, keepdims=True)) # 避免数值溢出
return exp_z / np.sum(exp_z, axis=0, keepdims=True)
def fit(self, X, y):
# 训练模型:X是特征矩阵(N x d), y是标签向量(N,),每个元素是类别索引
N = X.shape[0]
y_one_hot = np.eye(self.num_classes)[y] # 转换为one-hot编码 (N x K)
for _ in range(self.max_iter):
# 前向传播
z = self.W @ X.T + self.b # 计算logits (K x N)
p = self.softmax(z) # 概率矩阵 (K x N)
# 计算损失(交叉熵)
loss = -np.mean(np.log(p[y_one_hot.T == 1] + 1e-8)) # 加小值防log(0)
# 反向传播:计算梯度
grad_z = p – y_one_hot.T # 梯度对z (K x N)
grad_W = grad_z @ X / N # 平均梯度 (K x d)
grad_b = np.mean(grad_z, axis=1, keepdims=True) # 平均梯度 (K x 1)
# 更新参数
self.W -= self.learning_rate * grad_W
self.b -= self.learning_rate * grad_b
return loss
def predict(self, X):
# 预测类别:返回概率最高的索引
z = self.W @ X.T + self.b
p = self.softmax(z)
return np.argmax(p, axis=0)
# 示例使用
if __name__ == "__main__":
# 假设有简单数据集:2个特征,3个类别
X_train = np.array([[1.0, 2.0], [2.0, 3.0], [3.0, 1.0]]) # 训练特征
y_train = np.array([0, 1, 2]) # 训练标签(类别索引)
# 创建并训练模型
model = SoftmaxRegression(num_classes=3, input_dim=2, learning_rate=0.1, max_iter=1000)
loss = model.fit(X_train, y_train)
print(f"训练损失: {loss:.4f}")
# 预测新样本
X_test = np.array([[1.5, 1.5]])
pred = model.predict(X_test)
print(f"预测类别: {pred[0]}")
 网硕互联帮助中心
网硕互联帮助中心




评论前必须登录!
注册