【Leetcode】随笔

文章目录

• • 题目一：目标和（LeetCode 494）
  • • 题目分析：
    • 解题思路：
    • 示例代码：
    • 代码解析：
  • 题目二：二叉树的层平均值（LeetCode 637）
  • • 题目分析：
    • 解题思路：
    • 示例代码：
    • 代码解析：
  • 题目三：零钱兑换 II（LeetCode 518）
  • • 题目分析：
    • 解题思路：
    • 示例代码：
    • 代码解析：

🌈你好呀！我是 山顶风景独好 🎈欢迎踏入我的博客世界，能与您在此邂逅，真是缘分使然！😊 🌸愿您在此停留的每一刻，都沐浴在轻松愉悦的氛围中。 📖这里不仅有丰富的知识和趣味横生的内容等您来探索，更是一个自由交流的平台，期待您留下独特的思考与见解。🌟 🚀让我们一起踏上这段探索与成长的旅程，携手挖掘更多可能，共同进步！💪✨

题目一：目标和（LeetCode 494）

题目分析：

给你一个非负整数数组 nums 和一个整数 target 。向数组中的每个整数前添加 ‘+’ 或 ‘-’ ，然后串联起所有整数，可以构造一个表达式。例如，nums = [2, 1] ，可以在 2 前添加 ‘+’ ，在 1 前添加 ‘-’ ，得到表达式 “+2-1” 。返回可以通过上述方法构造的、运算结果等于 target 的不同表达式的数目。例如：输入nums = [1,1,1,1,1], target = 3，输出5。

解题思路：

问题转换：设添加’+‘的数字和为x，添加’-'的数字和为y，则x – y = target，且x + y = sum(nums)。联立得x = (target + sum(nums)) / 2，因此问题转化为求数组中能凑成x的子集数量（0-1背包问题）。 动态规划：定义dp[i]为能凑成和为i的子集数量，初始化dp[0] = 1（空子集和为0）。 状态转移：对于每个数字num，从x逆序遍历到num，更新dp[i] += dp[i – num]。 边界检查：若sum(nums) < target或(target + sum(nums))为奇数，则无解，返回0。

示例代码：

def findTargetSumWays(nums, target):
total = sum(nums)
# 边界条件：总和小于目标值或无法整除，无解
if total < abs(target) or (total + target) % 2 != 0:
return 0
# 计算需要凑成的和x
x = (total + target) // 2
# 初始化dp数组，dp[i]表示凑成和为i的子集数量
dp = [0] * (x + 1)
dp[0] = 1 # 空子集和为0

for num in nums:
# 逆序遍历，避免重复使用当前数字
for i in range(x, num – 1, –1):
dp[i] += dp[i – num]

return dp[x]

# 测试示例
if __name__ == "__main__":
nums = [1, 1, 1, 1, 1]
target = 3
print("目标和的表达式数目：", findTargetSumWays(nums, target)) # 输出：5

代码解析：

通过数学推导将目标和问题转化为子集和问题，降低问题复杂度。 dp数组的大小为x + 1，其中x是需要凑成的和，dp[i]记录凑成和i的方法数。 遍历每个数字时，采用逆序更新dp数组（从x到num），确保每个数字只被使用一次（0-1背包特性）。 时间复杂度为O(n×x)（n为数组长度，x为目标和），空间复杂度为O(x)（dp数组大小）。

题目二：二叉树的层平均值（LeetCode 637）

题目分析：

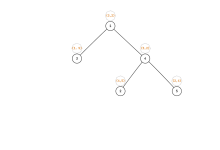
给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差10⁻⁵以内的答案可以被接受。例如：输入root = [3,9,20,null,null,15,7]，输出[3.00000,14.50000,11.00000]。

解题思路：

层序遍历：利用广度优先搜索（BFS）遍历每一层节点，计算每层的平均值。 队列辅助：使用队列存储当前层的节点，每次遍历队列中所有节点，计算总和与节点数，得到平均值。 遍历过程：初始化队列并加入根节点，循环处理每一层，计算平均值后将下一层节点（左右子节点）加入队列。

示例代码：

from collections import deque

# 二叉树节点定义
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right

def averageOfLevels(root):
if not root:
return []

result = []
q = deque([root]) # 初始化队列，加入根节点

while q:
level_size = len(q) # 当前层的节点数
level_sum = 0.0 # 当前层的总和

# 遍历当前层的所有节点
for _ in range(level_size):
node = q.popleft()
level_sum += node.val

# 加入下一层节点
if node.left:
q.append(node.left)
if node.right:
q.append(node.right)

# 计算当前层的平均值并加入结果
result.append(level_sum / level_size)

return result

# 辅助函数：构建二叉树（同前）
def build_tree(values):
if not values:
return None
root = TreeNode(values[0])
queue = [root]
i = 1
while queue and i < len(values):
node = queue.pop(0)
if values[i] is not None:
node.left = TreeNode(values[i])
queue.append(node.left)
i += 1
if i < len(values) and values[i] is not None:
node.right = TreeNode(values[i])
queue.append(node.right)
i += 1
return root

# 测试示例
if __name__ == "__main__":
# 构建示例树：[3,9,20,null,null,15,7]
values = [3,9,20,None,None,15,7]
root = build_tree(values)
print("每层节点的平均值：", averageOfLevels(root)) # 输出：[3.0, 14.5, 11.0]

代码解析：

通过层序遍历（BFS）实现，队列存储每一层的节点，level_size记录当前层节点数量。 遍历当前层节点时，累加节点值得到level_sum，计算平均值后加入结果列表。 下一层节点按左右顺序加入队列，确保层序遍历的正确性。 时间复杂度为O(n)（n为节点总数，每个节点访问一次），空间复杂度为O(n)（队列最多存储一层节点）。

题目三：零钱兑换 II（LeetCode 518）

题目分析：

给你一个整数数组 coins 表示不同面额的硬币，另给一个整数 amount 表示总金额。计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额，返回 0 。假设每一种面额的硬币有无限个。例如：输入coins = [1,2,5], amount = 5，输出4（组合为：[1,1,1,1,1]、[1,1,3]无效→正确为[1,1,1,2]、[1,2,2]、[5]）。

解题思路：

动态规划：定义dp[i]为凑成金额i的组合数，初始化dp[0] = 1（空组合）。 状态转移：对于每个硬币面额coin，从coin到amount正序遍历，更新dp[i] += dp[i – coin]（累加使用当前硬币的组合数）。 遍历顺序：先遍历硬币，再遍历金额，确保每个组合的硬币顺序唯一（避免重复计数，如[1,2]和[2,1]视为同一组合）。

示例代码：

def change(amount, coins):
# 初始化dp数组，dp[i]表示凑成金额i的组合数
dp = [0] * (amount + 1)
dp[0] = 1 # 基础情况：凑0元有1种方法（不选任何硬币）

# 遍历每种硬币
for coin in coins:
# 正序遍历金额，确保每个硬币可以被多次使用
for i in range(coin, amount + 1):
dp[i] += dp[i – coin]

return dp[amount]

# 测试示例
if __name__ == "__main__":
coins = [1, 2, 5]
amount = 5
print("凑成金额{}的组合数：".format(amount), change(amount, coins)) # 输出：4

代码解析：

dp数组的大小为amount + 1，dp[0]初始化为1表示凑0元只有1种方法（空组合）。 外层循环遍历每种硬币，内层循环从硬币面额开始正序遍历金额，确保每个硬币可以被重复使用（完全背包特性）。 dp[i]的更新逻辑为累加使用当前硬币的组合数（即dp[i – coin]），最终dp[amount]即为所求组合数。 时间复杂度为O(amount×k)（k为硬币种类数），空间复杂度为O(amount)（dp数组大小）。

✨ 这就是今天要分享给大家的全部内容了，我们下期再见！😊 🏠 我在CSDN等你哦！我的主页😍