卫星轨道基础知识
1. 引言
卫星轨道是描述人造卫星或自然天体(如月球、行星)在引力作用下运动路径的数学模型。理解卫星轨道的定义、类型和关键参数对于航天任务设计、卫星通信、导航和遥感等领域至关重要。本文将系统介绍卫星轨道的基本概念、分类方法以及决定轨道特性的关键参数。
2. 卫星轨道的定义
卫星轨道是指卫星在空间中的运动轨迹,由 开普勒定律 和 牛顿力学 共同描述。在理想情况下(忽略摄动力),卫星的运动遵循开普勒轨道模型,其核心特征包括:
- 椭圆性:大多数轨道是椭圆,中心天体(如地球)位于椭圆的一个焦点上。
- 守恒量:轨道能量(半长轴)、角动量(轨道平面取向)和偏心率是守恒的。
- 周期运动:卫星绕中心天体的运行周期由轨道半长轴决定。
3. 卫星轨道的分类
卫星轨道可按多种方式分类,常见的分类标准包括 形状、倾角、高度和功能。
3.1 按轨道形状分类
| 圆形轨道 | ( e = 0 ) | 半径恒定,速度均匀 | 地球观测、通信卫星(如GPS) |
| 椭圆轨道 | ( 0 < e < 1 ) | 近地点速度最快,远地点最慢 | 莫尼亚轨道(Molniya)、闪电轨道 |
| 抛物线轨道 | ( e = 1 ) | 逃逸轨道,理论上无限远 | 深空探测(脱离地球引力) |
| 双曲线轨道 | ( e > 1 ) | 星际飞行,不受中心天体束缚 | 星际探测器(如旅行者号) |
3.2 按轨道倾角分类
| 赤道轨道 | i=0∘i = 0^\\circi=0∘ | 沿赤道运行 | 地球静止卫星(GEO) |
| 倾斜轨道 | 0∘<i<90∘0^\\circ < i < 90^\\circ0∘<i<90∘ | 与赤道成一定角度 | 国际空间站(ISS,~51.6°) |
| 极地轨道 | i≈90∘i \\approx 90^\\circi≈90∘ | 覆盖全球两极 | 气象卫星(如NOAA系列) |
| 逆行轨道 | i>90∘i > 90^\\circi>90∘ | 与地球自转反向 | 部分间谍卫星 |
3.3 按轨道高度分类
| 低地球轨道(LEO) | 160–2,000 km | 周期短(90–120分钟),速度快 | 遥感(如Sentinel)、星链(Starlink) |
| 中地球轨道(MEO) | 2,000–35,786 km | 中等覆盖范围,周期较长 | 导航卫星(GPS、伽利略) |
| 地球静止轨道(GEO) | 35,786 km | 周期=24小时,相对地面静止 | 通信卫星(如Intelsat) |
| 高椭圆轨道(HEO) | 远地点>35,786 km | 长时间覆盖高纬度地区 | 俄罗斯莫尼亚轨道(Molniya) |
4. 卫星轨道的关键参数(开普勒根数)
卫星轨道的数学描述通常采用 六个轨道根数(开普勒参数),分为 几何参数 和 时间参数:
4.1 几何参数(描述轨道形状和空间取向)
半长轴(a)
- 定义:椭圆轨道长轴的一半,决定轨道大小和周期。
- 公式:T2∝a3T^2 \\propto a^3T2∝a3(开普勒第三定律)。
- 示例:GEO卫星的 a≈42,164 kma \\approx 42,164 \\text{ km}a≈42,164 km。
偏心率(e)
- 定义:描述轨道的“扁度”,e=1−b2a2e = \\sqrt{1 – \\frac{b^2}{a^2}}e=1−a2b2(b为半短轴)。
- 示例:近地圆轨道 e≈0e \\approx 0e≈0,莫尼亚轨道e≈0.7e \\approx 0.7e≈0.7。
轨道倾角(i)
- 定义:轨道平面与参考平面(如赤道面)的夹角。
- 示例:极地卫星 i=90∘i = 90^\\circi=90∘,ISS i≈51.6∘i \\approx 51.6^\\circi≈51.6∘。
升交点赤经(Ω)
- 定义:轨道升交点(卫星从南向北穿越赤道)相对于春分点的角度。
- 作用:确定轨道平面在空间中的方位。
近地点幅角(ω)
- 定义:近地点相对于升交点的角度,描述椭圆轨道的长轴方向。
- 示例:若 ω=0∘\\omega = 0^\\circω=0∘,近地点在升交点处。
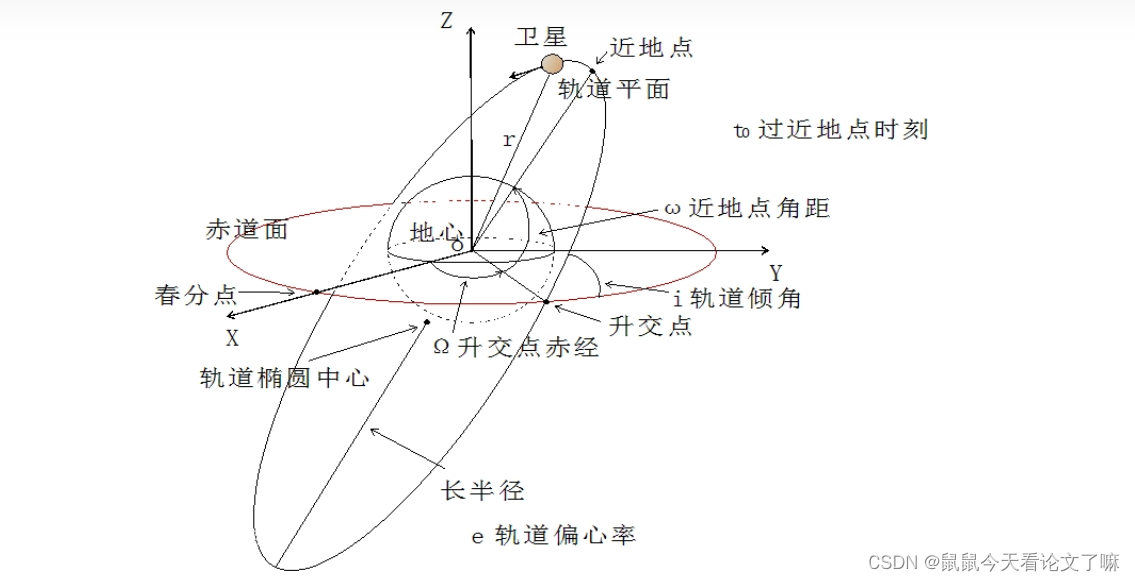
4.2 时间参数(描述卫星在轨道上的位置)
- 真近点角(ν):卫星当前位置与近地点的夹角(瞬时位置)。
- 平近点角(M):用于计算卫星位置的虚拟角度,M=n(t−t0)M = n(t – t_0)M=n(t−t0)(n为平均运动角速度)。
- 关系:通过 开普勒方程 M=E−esinEM = E – e \\sin EM=E−esinE 关联偏近点角(E)和真近点角(ν)。
5. 实际应用中的轨道摄动
理想开普勒轨道仅适用于二体问题,实际卫星轨道受多种摄动影响:
- 地球非球形引力(J₂项):导致轨道进动(如GEO卫星的经度漂移)。
- 大气阻力(LEO卫星):轨道高度缓慢衰减。
- 日月引力(HEO/GEO卫星):长期影响轨道倾角。
- 太阳光压:对大型卫星(如Hubble)产生微小推力。
解决方法:采用 平均轨道根数 或 数值积分(如SGP4模型) 进行高精度预测。
6. 总结
- 卫星轨道由 形状、倾角、高度 等特征分类,不同轨道适用于不同任务(通信、导航、遥感)。
- 六个开普勒根数(a, e, i, Ω, ω, ν/M)完整描述轨道几何和卫星位置。
- 实际轨道需考虑摄动效应,并通过动力学模型修正。
理解这些概念是卫星任务设计、轨道控制和数据分析的基础。随着商业航天的兴起(如Starlink、OneWeb),高效轨道管理变得愈发重要。
 网硕互联帮助中心
网硕互联帮助中心


评论前必须登录!
注册