Root was Built by Love, Broken by Destiny-根因爱而生，因命运而断

D.根因爱而生，因命运而断

每次测试时限：2 秒

每次测试的内存限制：256 兆字节

输入：标准输入

输出：标准输出

目录

前言

题目

二、思路

标程（官方代码）

总结

前言

我认为的一道很好很有价值的题

来了，爱了，给了她一颗星星，走了。

                                        ——刘慈欣《三体》

题目

心瀑河横贯德斯坦乐园，将其分为南北两侧。

根工程师想要在河边建造 n 座房子，编号从 1 到 n 。北边的所有房屋和南边的所有房屋都必须沿着与心瀑河平行的直线建造。

将有 m 座桥梁，其中 i (th)座桥梁连接着 ui 号房屋和 vi 号房屋( ui≠vi )。可以保证所有 n 个房子都被这些桥连接起来，也就是说，你可以通过过桥从任何一个房子到达另一个房子。而且，没有两座桥连接同一对房子。

根想知道有多少种沿河排列 n 座房子的方法，模数为 109+7 ，使得以下条件对规划的 m 座桥梁成立：

• 对于每一座桥，它所连接的两座房子都位于河的两岸；
• 在房屋之间画直线时，桥梁不会交叉。

 当 n=5 时可能的房屋排列。

如果以下条件中至少有一个成立，那么这两种排列就被认为是不同的：

• 在每种排列中，都存在位于不同边上的房子；
• 存在两座房子 a 和 b ，这两座房子在两个排列中都位于同一边，但是在一个排列中 a 位于 b 之前，而在另一个排列中 b 位于 a 之前。

由于根被他的前女友所困扰，命运将他与前女友分开，因此他要求你计算沿河排列房屋的方式数，模数为 1e9+7 。

输入

每个测试包含多个测试用例。第一行包含测试用例的数量 t ( 1≤t≤104 )。测试用例说明如下。

每个测试用例的第一行包含两个整数 n 和 m ( 2≤n≤2⋅105 , n−1≤m≤min(n(n−1)2,2⋅105) )–房屋数量和桥梁数量。

接着是 m 行，其中 i /行包含两个整数 ui 和 vi ( 1≤ui,vi≤n , ui≠vi )–即 i /桥所连接的两座房屋。

可以保证所有的 n 房子都被桥连接起来，而且没有两座桥连接同一对房子。

保证所有测试用例的 n 之和不超过 2e5 ，所有测试用例的 m 之和不超过 2e5 。

输出

对于每个测试用例，输出一个整数 – 沿河排列 n 座房屋的方式数，模数为 109+7 。

二、思路

  于我非常惊艳的思路，赛时没有想出来。

https://codeforces.com/blog/entry/145357

我们可以证明，Destinyland 的地图不包含循环。

请看下面的地图：  

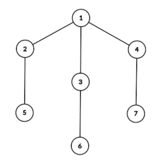
证明只有当且仅当一棵树不包含类似于所示的子树时，它才是有效的 "目的地 "图。

如果我们把 Destinyland 树的所有叶子都去掉，剩下的图形就会形成一条简单的路径。

假设 G 是目的地图的图形。

如果 G 的子图 H 不可能是有效的 "目的地 "图，那么 G 本身也不可能是有效的。

为了证明这一点，请假设 G 有效，而 H 无效。那么，通过删除不在 H 中的顶点和边，我们得到的子图 H 也应该是有效的。但事实并非如此！这与我们的假设相矛盾，所以 G 也不可能有效。

定理 1： 任何长度的循环都不能**是有效的 "目的地 "图。 证明： 假设相反。假设 v 是北边最左边的房子。它在南边有两个邻居。左边的房子是 L ，另一个是 R 。由于 L 除了 v 之外肯定还有另一个邻居，该邻居不可能在南侧，因此它肯定在北侧。然而，由于 v 是最左边的节点，所以这个邻居必须在 v 的右边，而 L 和这个邻居之间的边将穿过边 v – L 。这一矛盾表明， L 除了 v 之外不可能有其他邻居，这与我们假设的图形是一个循环相矛盾。

定理 2： 下面这棵树不可能是有效的目的地图：

 证明： 顶点 2 、 3 和 4 都位于顶点 1 的对边。如果我们将它们从左到右依次排列为 u1 、 u2 和 u3 ，那么 u2 的邻边必然会与边 1 – u1 或 1 – u3 形成交叉。因此，不可能将这棵树的顶点排列成有效的 Destinyland 布局。

根据等式 1 和等式 2，我们可以得出如下结论：

• G 一定是一棵树。
• G 中没有顶点与三个或三个以上的非叶子邻接点相连。

现在，删除所有叶节点。由于这些叶节点始终是非剪切顶点(即它们的移除不会断开树的连接)，剩余的图形(如果存在的话)仍然是连接的。由于所有剩余顶点的度数最多为 2 。所以得到的结构一定是路径。

情况 1： 移除树叶后，图变成空的。 在这种情况下，原始图形只有一条边。所以答案就是 2 。

情况 2： 只剩下一个顶点。 在这种情况下，原来的树是一颗星。根据我们把中心顶点放在哪一边，以及如何排列叶子，答案是： 2×(n−1)! 。

情况 3： 剩下两个相连的非叶顶点 u 和 v 。 在这种情况下，有 4 种有效的放置方式，这取决于哪一个顶点位于北侧，以及它们相邻的叶子是如何围绕另一个顶点排列的。(注：** u 和 v 不可能在对方的两边都有邻接叶）。 所以答案是： 4×(du−1)!×(dv−1)! ，其中 du 和 dv 分别是 u 和 v 的度数。

案例 4： 剩下的结构是一条长度至少为 3 的路径。 在这种情况下，我们有 4 种有效的放置方法。这取决于将哪些顶点放置在北侧，以及如何放置至少有两个顶点的一侧的两个顶点。(由于该路径至少有 3 个顶点，因此不存在冲突）。

现在，我们只需要安排与每个顶点相邻的叶子的相对位置。因为它们相对于其他顶点的位置只取决于主路径的四种排列方式。这一点的证明很枯燥，我们就不多说了:)

假设 S 是路径上的顶点集合，假设 Sahai 是连接顶点 i 的叶子数。那么有效布局的总数为 4×∏r∈S(Sahar!)

实现解法

整个算法的运行时间为 O(n) 。！！！

标程（官方代码）

#include <bits/stdc++.h>
using namespace std;

#define SZ(x) int(x.size())

const int MOD = 1e9 + 7;
const int MXN = 2e5 + 5;

int n, m, fact[MXN];
vector<int> adj[MXN];

int32_t main() {
cin.tie(0); cout.tie(0); ios_base::sync_with_stdio(0);
fact[0] = 1;
for (int i = 1; i < MXN; i++)
fact[i] = (1ll * fact[i-1] * i) % MOD;
int T;
cin >> T;
while (T–) {
cin >> n >> m;
for (int i = 1; i <= n; i++) adj[i].clear();
for (int i = 1; i <= m; i++) {
int u, v;
cin >> u >> v;
adj[u].push_back(v);
adj[v].push_back(u);
}

long long ans = 2;
int tl = 0;
if (m >= n) ans = 0;
for (int u = 1; u <= n; u++) {
if (adj[u].size() > 1) {
int x = 0;
for (int v : adj[u]) {
x += (SZ(adj[v]) == 1);
}
if (x >= SZ(adj[u]) – 2) (ans *= fact[x]) %= MOD;
else ans = 0;
} else tl ++;
}
if (tl < n-1) tl = 2; else tl = 1;
cout << (ans * tl % MOD) << '\\n';
}
return 0;
}

总结

thank you for listen ,喜欢的话点个赞吧

我说，你最喜欢哪个季节？”

“秋天”“为什么不是春天”

“春天，好多感觉挤在一起，累人呢，秋天多好”

“倒不如说郁郁葱葱得让人嫉妒”